情報制御基礎2018全講義録
- 制御構文について
- 大域変数・局所変数・スコープ
- 実数の注意点
- 実数の注意点・回答編
- 実数の扱い・レポート-No.1
- 入出力リダイレクト
- 入出力と変数・レポートNo.2
- D/A変換回路とA/D変換回路
- 移動平均の処理
- 移動平均のプログラム
- 様々な移動平均
- 様々な移動平均・レポート-No.3
- 変化の検出・差分処理
- 差分計算・レポート-No.4
- 制御工学とまとめ
注意:2018/07/30(Mon)前期期末テスト・情報制御基礎は、A4✕1枚の手書き資料のみ、持ち込み可とする。
オブジェクト指向とソフトウェア工学
オブジェクト指向プログラミングの最後の総括として、 ソフトウェア工学との説明を行う。
トップダウン設計とウォーターフォール型開発
ソフトウェア工学でプログラムの開発において、一般的なサイクルとしては、 専攻科などではどこでも出てくるPDCAサイクル(Plan, Do, Check, Action)が行われる。 この時、プログラム開発の流れとして、大企業でのプログラム開発では一般的に、 トップダウン設計とウォーターフォール型開発が行われる。
トップダウン設計では、全体の設計(Plan)を受け、プログラムのコーディング(Do)を行い、 動作検証(Check)をうけ、最終的に利用者に納品し使ってもらう(Action)…の中で、 開発が行われる。設計の中身も機能仕様や動作仕様…といった細かなフェーズになることも多い。 この場合、コーディングの際に設計の不備が見つかり設計のやり直しが発生すれば、 全行程の遅延となることから、前段階では完璧な動作が必要となる。 このような、上位設計から下流工程にむけ設計する方法は、トップダウン設計などと呼ばれる。また、処理は前段階へのフィードバック無しで次工程へ流れ、 川の流れが下流に向かう状態にたとえ、ウォーターフォールモデルと呼ばれる。

引用:Think IT 第2回開発プロセスモデル
このウォーターフォールモデルに沿った開発では、横軸時間、縦軸工程とした ガントチャートなどを描きながら進捗管理が行われる。

引用:Wikipedia ガントチャート
一方、チェック工程(テスト工程)では、 要件定義を満たしているかチェックしたり、設計を満たすかといったチェックが存在し、 テストの前工程にそれぞれ対応したチェックが存在する。 その各工程に対応したテストを経て最終製品となる様は、V字モデルと呼ばれる。
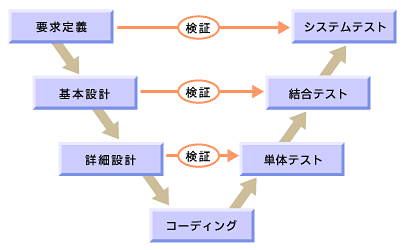
引用:@IT Eclipseテストツール活用の基礎知識
しかし、ウォーターフォールモデルでは、前段階の設計の不備があっても前工程に戻るという考えをとらないため、全体のPDCAサイクルが終わって次のPDCAサイクルまで問題が残ってしまう。 巨大プロジェクトで大量の人が動いているだから、簡単に方針が揺らいでもトラブルの元にしかならないことから、こういった手法は大人数巨大プロジェクトでのやり方。
ボトムアップ設計とアジャイル開発
少人数でプログラムを作っている時(あるいはプロトタイプ的な開発)には、 部品となる部分を完成させ、それを組合せて全体像を組み上げる手法もとられる。 この方法は、ボトムアップ設計と呼ばれる。このような設計は場当たり的な開発となる場合があり設計の見直しも発生しやすい。
また、ウォーターフォールモデルでは、前工程の不備をタイムリーに見直すことができないが、 少人数開発では適宜前工程の見直しが可能となる。 特にオブジェクト指向プログラミングを実践して隠蔽化が正しく行われていれば、 オブジェクト指向によるライブラリの利用者への影響を最小にしながら、ライブラリの内部設計の見直しも可能となる。 このような外部からの見た挙動を変えることなく内部構造の改善を行うことはリファクタリングと呼ばれる。
一方、プログラム開発で、ある程度の規模のプログラムを作る際、最終目標の全機能を実装したものを 目標に作っていると、全体像が見えずプログラマーの達成感も得られないことから、 機能の一部分だけ完成させ、次々と機能を実装し完成に近づける方式もとられる。 この方式では、機能の一部分の実装までが1つのPDCAサイクルとみなされ、 このPDCAサイクルを何度も回して機能を増やしながら完成形に近づける方式とも言える。 このような開発方式は、アジャイルソフトウェア開発と呼ぶ。 一つのPDCAサイクルは、アジャイル開発では反復(イテレーション)と呼ばれ、 短い開発単位を繰り返し製品を作っていく。この方法では、一度の反復後の実装を顧客に見てもらい、 顧客とプログラマーが一体となって開発が行われる。
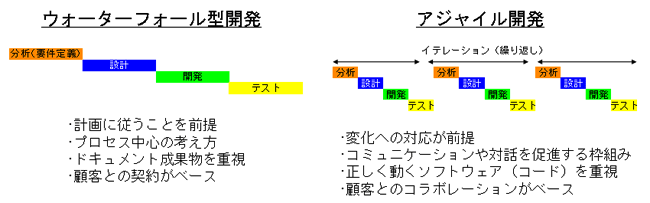
引用:コベルコシステム
エクストリームプログラミング
アジャイル開発を行うためのプログラミングスタイルとして、 エクストリームプログラミング(Xp)という考え方も提唱されている。 Xpでは、5つの価値(コミュニケーション,シンプル,フィードバック,勇気,尊重)を基本とし、 開発のためのプラクティス(習慣,実践)として、 テスト駆動開発(コーディングでは最初に機能をテストするためのプログラムを書き、そのテストが通るようにプログラムを書くことで,こまめにテストしながら開発を行う)や、 ペアプログラミング(2人ペアで開発し、コーディングを行う人とそのチェックを行う人で役割分担をし、 一定期間毎にその役割を交代する)などの方式が取られることが多い。
リーン開発は、品質の良いものを作る中で無駄の排除を目的とし、本当にその機能は必要かを疑いながら、優先順位をつけ実装し、その実装が使われているのか・有効に機能しているのかを評価ながら開発をすすめる。
伽藍とバザール
これは、通常のソフトウェア開発の理論とは異なるが、重要な開発手法の概念なので「伽藍とバザール」を紹介する。
伽藍とは、優美な寺院のことであり、その設計・開発は、優れた設計・優れた技術者により作られた完璧な実装を意味している。バザールは有象無象の人の集まりの中で作られていくものを意味している。
たとえば、伽藍方式の代表格である Microsoft の製品は、優秀なプロダクトだろうが、中身の設計情報などを普通の人は見ることはできない。これに対しバザール方式の代表格の Linux は、インターネット上にソースコードが公開され、誰もがソースコードに触れプログラムを改良してもいい。その中で、新しい便利な機能を追加しインターネットに公開されれば、良いコードは生き残り、悪いコードは淘汰されていく。
バザール方式は、オープンソースライセンスにより成り立っていて、このライセンスが適用されていれば、改良した機能はインターネットに公開する義務を引き継ぐ。このライセンスの代表格が、GNU パブリックライセンス(GPL)であり、公開の義務の範囲により、BSD ライセンス、Apacheライセンスといった違いがある。


制御工学とまとめ
情報制御基礎の授業を通して、入力値を制御するため、コンピュータを使う場合の数値処理の基礎的な話として、信号の平滑化や差分について説明をしてきた。実際には、入力値を制御に利用する場合には、数学的バックグラウンドも必要となる。
制御工学の概要
以下に、制御工学ではどのようなことを行うのか、概要を述べる。
ここで紹介する制御理論は、古典制御理論と呼ばれる。
制御工学では、入力値と、何らかの処理を施し出力値
が得られるシステムで、どのように制御するかを考える。
例えば、電気ポットの温度制御をする場合、設定温度の値を入力値(x)とし、何らかの処理を行い、出力となるヒーターの電流を制御し、最終的には温度(y)が測定される。ヒーターは、設定温度(x)と温度計の値(y)の差に応じて電流量を変化させる。このように一般的な制御では、最終的な温度が入力に戻っている。このように目標値に近づけるために、目標値との差をとって制御することをフィードバック制御という。
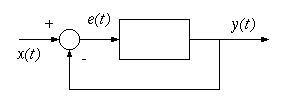
入力と出力で制御された波形の例を示す。
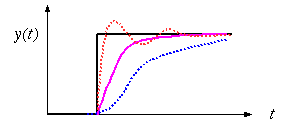
この波形では、黒のように入力値が変化した場合、それに追いつこうと出力が変化する。(1)理想的には、速やかに追いつく赤のように変化したい。しかし、(2)変化への制動が大きい過制動(青点線)では、目標値に追いつくまでに時間がかかる。(3)一方ずれに対して制御が激しいと目標値を追い越したり、増えすぎ分を減らしすぎたり変動する過制御(赤点線)となる。
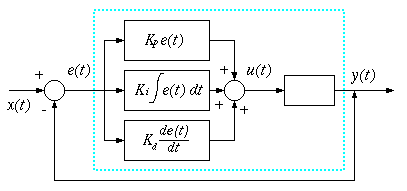
PID制御
目標値、出力
、ずれ(偏差)
、制御量
とした時、基本的なフィードバック制御として偏差の使い方によってP動作,I動作,D動作がある。参考 Wikipedia PID制御
比例制御(P制御)
偏差に比例した制御(Kp は比例ゲイン)
積分制御(I制御)
偏差のある状態が長い時間続く場合、入力値の変化を大きくすることで目標値に近づけるための制御。(Ki は積分ゲイン)
微分制御(D制御)
急激な出力値の変化が起こった場合、その変化の大きさに応じて妨げようとする制御。(Kd は微分ゲイン)
PID制御
上記のI制御やD制御だけでは、安定することはなく、これらを組み合わせたPID制御を行う。
この中で、の値は、制御が最も安定するように調整を行うものであり、数値シミュレーションや、ステップ応答を与えた時の時間的変化を測定して調整を行う。
差分計算・レポート-No.4
前回の「差分」の講義における、波形データから、山の数をカウントする処理を記述せよ。
# 授業では結果が「4つの山」としていたが、計算方法が明記されていれば、異なる結果でもよい。
処理は、C言語などのプログラムで記述しても、表計算ソフトでの式による計算でも良い。表計算ソフトを用いる場合は、どのような式を入れてあるか具体的な式について明記してあること。
レポートでは、計算方法が判るプログラムリスト(もしくは表計算ソフトの式がわかるもの)と、その説明。および結果(全データでなくても良く、山としてカウントした部分の近辺のデータ)と、考察を記述すること。
UML振る舞い図
参考資料図をもとに振る舞い図の説明を行う。
ユースケース図

ユーザなど外部からの要求に対する、システムの振る舞いを表現するための活用事例を表す図がユースケース図。 システムを構築する際に、最初に記述するUMLであり、システムに対する処理要件の全体像を理解するために記述する。 ユーザや外部のシステムは、アクターとよび人形の絵で示す。楕円でシステムに対する具体的な処理をユースケースとして記述する。 関連する複数のユースケースをまとめて、サブジェクトとして示す場合もある。
アクティビティ図
処理順序を記述するための図にはフローチャートがあるが、上から下に処理順序を記述するため、縦長の図になりやすい。また、四角枠の中に複雑なことを書けないので、UMLではアクティビティ図を用いる。
初期状態から、終了状態までの手順を示すためのがアクティビティ図。 複数の処理を並行処理する場合には、フォークノードで複数の処理を併記し、最終的に1つの処理になる部分をマージノードで示す。 通常の処理は、角丸の長方形で示し、条件分岐はひし形で示す。
ステートチャート図(状態遷移図)
ステートチャート図は、処理内部での状態遷移を示すための図。 1つの状態を長丸長方形で示し、初期状態から終了状態までを結ぶ。 1つの状態から、なんらかの状態で他の状態に遷移する場合は、分岐条件となる契機(タイミング)とその条件、およびその効果(出力)を「契機[条件]/効果」で矢印に併記する。 複数の状態をグループ化して表す場合もある。
シーケンス図
複数のオブジェクトが相互にやり取りをしながら処理が進むようなものを記述するためのものがシーケンス図。 上部の長方形にクラス/オブジェクトを示し、その下に時系列の処理の流れの線(Life Line)を描く。 オブジェクトがアクティブな状態は、縦長の長方形で示し、そのLife Line間を、やり取り(メッセージ)の線で相互に結ぶ。 メッセージは、相手側からの返答を待つような同期メッセージは、黒塗り三角矢印で示す。 返答を待たない非同期メッセージは矢印で示し、返答は破線で示す。
コミュニケーション図
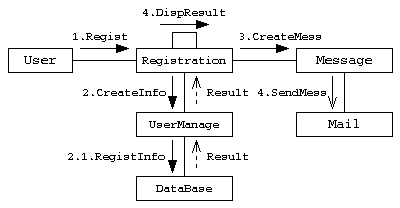
クラスやオブジェクトの間の処理とその応答(相互作用)と関連の両方を表現する図。