図形と仮想関数の継承方法
純粋仮想基底クラスと図形の課題の基本形
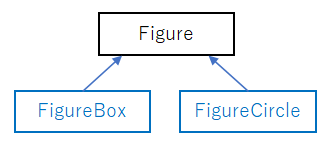
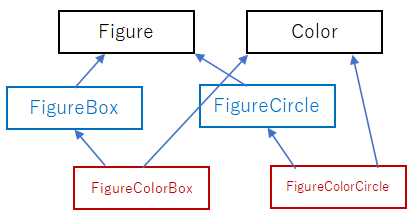
課題で取り組んでいるプログラムは、純粋仮想基底クラスFigureと、そこから派生させたクラスと仮想関数で絵を書いている。このような派生の関係を以下のような図で表現する。
class Figure {
public:
virtual void draw( int x , int y ) = 0 ;
} ;
class FigureBox : public Figure {
private:
int width , height ;
public:
FigureBox( int w , int h ) : width( w ) , height( h ) {}
virtual void draw( int x , int y ) {
// 四角を描く処理
}
} ;
class FigureCircle : public Figure {
private:
int radius ;
public:
FigureCircle( int r ) : radius( r ) {}
virtual void draw( int x , int w ) {
// 円を描く処理
}
} ;
色付き図形を派生する方法
課題では、上記プログラムを活用して、色付き図形のクラスを作ることを目的とするが、その実装方法には色々な方法がある。
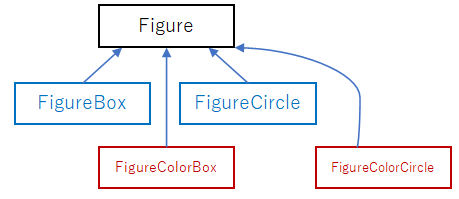
単純なやり方は、FigureBox と同じように、Figure から FigureColorBox を派生させる方法だろう。
class FigureColorBox : public Figure {
private:
int width , height , color ;
public:
FigureColorBox( int w , int h , int c )
: width( w ) , height( h ) , color( c ) {}
virtual void draw( int x , int y ) {
// 色を変える処理
// 四角を描く処理 ... FIgureBox と同じ処理
}
} ;
この方法は単純だけど、四角を描く処理を書くため無駄であり、FIgureBox と処理を共通化できればプログラムを書く手間を減らせるはず。
処理を共通化するなら派生すればいい
class FigureColorBox : public FigureBox {
private:
int color ; // 幅と高さの記述が無い
public:
FigureColorBox( int w , int h , int c )
: FigureBox( w , h ) , color( c ) {}
virtual void draw( int x , int y ) {
// 色を変える処理
FigureBox::draw( x , y ) ; // 親クラスの処理を継承
}
} ;
同じような色の処理を追加したクラスが沢山ある場合
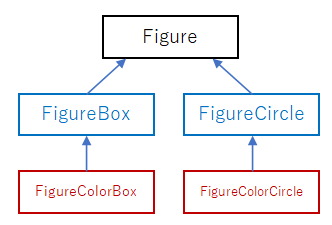
上記の、FigureBox から FigureColorBox を派生させた場合は、四角を描く処理が継承により共通化ができた。
しかし、同じように FigureCircle から FigureColorCircle を派生させる…といったクラスを沢山作る場合は、色を変える処理を何度も使うことになるが、処理の共有することができない。こういった場合は、以下のような方法がある。
class Color {
private:
int color ;
public:
Color( int c ) : color( c ) {}
void set_color() {
// 色を変える処理
}
} ;
class FigureColorBox : public FigureBox , public Color {
public: // 多重継承のキモ
FigureColorBox( int w , int h , int c )
: FigureBox( w , h ) , Color( c ) {}
virtual void draw( int x , int y ) {
Color::set_color() ; // Colorクラスを使って色を設定
FigureBox::draw( x , y ) ; // FigureBoxクラスで形を描く
}
} ;
多重継承
上記の FigureColorBox のように、親クラスとして、FigureBox と Color のように複数のクラスをもつ継承は、多重継承と呼ばれる。
ただし、多重継承は後に示すような曖昧さや、実装の際の手間を考えると、多重継承は必ずしも便利な機能ではない。このため、オブジェクト指向のプログラミング言語によっては、多重継承機能が使えない。
Java では、多重継承が使えない代わりに、interface 機能が使えたりする。
ダイヤモンド型の継承と曖昧さ
C++ のような言語での多重継承が問題となる事例として、ダイヤモンド型の継承が挙げられる。
 |
 |
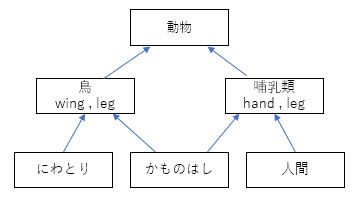
例えば、動物クラスから鳥クラス・哺乳類クラスを派生して、鳥クラスからニワトリを派生して、哺乳類クラスから人間を派生するというのは、進化の過程を踏まえると、自然な派生と考えられる。
しかし、鳥がクラスメンバーとして羽と足を持ち、哺乳類が手と足を持つとしたとき、鳥のくちばしを持ち卵を生むカモノハシを派生する場合には、どうすれば良いのだろうか?しかし、これを鳥と哺乳類を親クラスとした多重継承で実装をすると、手と羽と足が4本のカモノハシができてしまう。(お前はドラゴンかッ!)
また、大元の動物クラスがインスタンスを持つ場合、このような多重継承をすると、同じ名前のインスタンスを2つ持つことになる。この場合、C++では仮想継承というメカニズムを使うことができる。
class Animal { private: char name[10] ; } ; class Bird : public virtual Animal { } ; class Mammalian : public virtual Animal { } ; class Psyduck : public Bird , public Mammalian { // このクラスは、name は1つだけ。 } ;
また、動物が動くためのmove()というメソッドを持つとした場合、鳥は羽で飛び、哺乳類は足で移動する処理となるだろう。しかし、多重継承のカモノハシは、鳥の羽で動くメソッドmove()と、哺乳類の足で動くメソッドmove()を持つことになり、カモノハシに動け…と命令した場合、どちらのメソッドmove() を使うのだろうか?
こういった、使いにくさ・実装時の手間・処理の曖昧さを考慮したうえで、多重継承のメカニズムが使えるオブジェクト指向プログラム言語は少ない。
リスト構造について
データ処理において、配列は基本的データ構造だが、動的メモリ確保の説明で述べたように、基本の配列では大きさを変更することができない。これ以外にも、配列は途中にデータを挿入・削除を行う場合、の処理時間を伴う。以下にその問題点を整理し、その解決策であるリスト構造について説明する。
配列の利点と欠点
今までデータの保存には、配列を使ってきたが、配列は添字で場所を指定すれば、その場所のデータを簡単に取り出すことができる。配列には苦手な処理がある。例えば、配列の中から目的のデータを高速に探す方式として、2分探索法を用いる。
int find( int array[] , int left , int right , int key ) {
// データは left から right-1までに入っているとする。
while( left < right ) {
int mid = (left + right) / 2 ; // 中央の場所
if ( array[ mid ] == key )
return mid ; // 見つかった
else if ( array[ mid ] > key )
right = mid ; // 左半分にある
else
left = mid + 1 ; // 右半分にある
}
return -1 ; // 見つからない
}
しかし、配列の中に新たに要素を追加しようとするならば、データは昇順に並んでいる必要があることから、以下のようになるだろう。
void entry( int array[] , int* psize , int key ) {
// データを入れるべき場所を探す処理
for( int i = 0 ; i < *psize ; i++ ) // O(N) の処理だけど、
if ( array[ i ] > key ) // O(log N) でも書けるけど
break ; // 単純に記載する。
if ( i < *psize ) {
// 要素を1つ後ろにずらす処理
for( int j = *psize ; j > i ; j-- ) // O(N)の処理
array[ j ] = array[ j - 1 ] ;
array[ i ] = key ;
} else {
array[ *psize ] = key ;
}
(*psize)++ ;
}
これで判るように、データを配列に追加する場合、途中にデータを入れる際にデータを後ろにずらす処理が発生する。
この例は、データを追加する場合であったが、不要となったデータを取り除く場合にも、データの場所の移動が必要である。
順序が重要なデータ列で途中へのデータ挿入削除
例えば、アパート入居者に回覧板を回すことを考える。この中で、入居者が増えたり・減ったりした場合、どうすれば良いか考える。
通常は、自分の所に回覧板が回ってきたら、次の入居者の部屋番号さえわかっていれば、回覧板を回すことができる。
101 102 103 104 105 106 [ 105 | 106 | -1 | 102 | 104 | 103 ]
このように次のデータの場所という概念を使うと、データの順序を持って扱うことができる。
struct LIST {
int data ;
int next ;
} ;
struct LIST array[] = {
/*0*/ { 11 , 2 } ,
/*1*/ { 67 , 3 } , // 末尾にデータ34を加える
/*2*/ { 23 , 4 } , // { 23 , 5 } ,
/*3*/ { 89 , -1 } , // 末尾データの目印
/*4*/ { 45 , 1 } ,
/*5*/ { 0 , 0 } , // { 34 , 4 } ,
} ;
for( int idx = 0 ; idx >= 0 ; idx = array[ idx ].next ) {
printf( "%d¥n" , array[ idx ].data ) ;
}
この方法を取れば、途中にデータ入れたり、抜いたりする場合に、データの移動を伴わない。
しかし、配列をベースにしているため、配列の上限サイズを超えて格納することはできない。
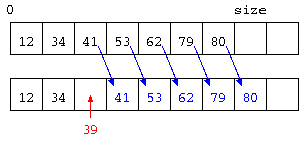
リスト構造
リスト構造は、データと次のデータへのポインタで構成され、必要に応じてメモリを確保することで、配列の上限が制限にならないようにする。また、次のデータへのポインタでつなげているため、途中へのデータ挿入が簡単にできるようにする。
struct List {
int data ;
struct List* next ;
} ;
struct List* top ;
top = (struct List*)malloc( sizeof( struct List ) ) ;
top->data = 111 ;
top->next = (struct List*)malloc( sizeof( struct List ) ) ;
top->next->data = 222 ;
top->next->next = (struct List*)malloc( sizeof( struct List ) ) ;
top->next->next->data = 333 ;
top->next->next->next = NULL ; // 末尾データの目印
struct List*p ;
for( p = top ; p != NULL ; p = p->next ) {
printf( "%d¥n" , p->data ) ;
}
補助関数
上記のプログラムでは、(struct…)malloc(sizeof(…))を何度も記載し、プログラムが分かりにくいので、以下に示す補助関数を使うと、シンプルに記載できる。
struct List* cons( int x , struct List* n ) {
struct List* ans ;
ans = (struct List*)malloc( sizeof( struct List ) ) ;
if ( ans != NULL ) {
ans->data = x ;
ans->next = n ;
}
return ans ;
}
struct List* top ;
top = cons( 111 , cons( 222 , cons( 333 , NULL ) ) ) ;
授業アンケートで板書の字が読みづらいといわれつつも、パッパッパッってコードを書いていると「その関数名読めない…」とツッコミが。cons : constructor の意味ですがな…と話しつつ、例年どおり「どーでもいいウンチク」を話す。
今日以降説明していくリスト構造は、古くから使われていて、LISP というプログラム言語があり、この言語でリスト(セル)を生成する関数が cons 。
LISPと関数型プログラミング言語
LISPの歴史は長く、最古のFORTRAN,COBOLに次ぐ3番目ぐらい。最初は、人工知能のプログラム開発のための関数型プログラミング言語として作られた。特徴として、データもプログラムもすべてリスト構造(S式)で表すことができ、プログラムは関数型に基づいて作られる。
関数型プログラミングは、Ruby や Python でも取り入れられている。関数型プログラミングは、処理を関数をベースに記述することで「副作用を最小限にすることができ」、極端な話をすればループも再帰呼出しで書けばいい…。
LISPの処理系は、最近では Scheme などが普通だが、プログラムエディタの Emacs は、内部処理が LISP で記述されている。
第29回高専プロコン予選通過
第29回高専プロコンの予選結果が公開されました。
福井高専からは、久々に課題部門・競技部門で予選通過となりました。
これからが忙しくなります。
課題部門
サバ×サバ
-サバで時代を生き延びる- 水上,森川,山本,指導:村田
自由部門
ポーズでプログラミング
-動きで動くロボット- 大瀬,道關,奥村,向井,村上,指導:小松
競技部門
自軍パネル破壊はテンポロス
永田,谷川,河野,指導:村田
前期中間テストの答案返却
前期中間試験の返却と解答の解説を行う。
今年の学生は、3年で私がプログラミング応用を担当していないので、私が例年3年に出題していた以下のような問題が苦手だろうということで、出題した問題。ポインタと構造体と配列が絡む問題は、式の意味を理解するためにも、C言語の演算子の優先順位などを踏まえ、こういった問題を知っておくべき。
また、上記のような問題では、C言語でのポインタと配列の意味を理解してもらうために、例年説明する極端なコーディングも紹介しておいた。
int a[5] = { 11 , 22 , 33 , 44 , 55 } ;
int* pi ;
pi = a + 2 ;
printf( "%d¥n" , *pi ) ; // *( pointer + offset )
printf( "%d¥n" , pi[0] ) ; // と pointer[ offset ] は同じ
printf( "%d¥n" , *(pi + 1) ) ; // 44
printf( "%d¥n" , pi[ 1 ] ) ; // 44
printf( "%d¥n" , (-1)[ pi ] ) ; // 22 = *( -1 + pi )
printf( "%c¥n" , "abcdef"[ 2 ] ) ; // c
「 printf( “%d¥n” , -1[ pi ] ) ; 」の結果が -44 になった。一瞬なんでや…って思ったけど、-( 1[pi] ) なのね。
数学解答システムWolframAlphaが日本語化
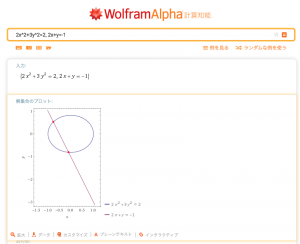
数学に特化した、Web質問・解答システムのWolframAlpha が日本語化されました。
「2x^2+3y^2=2, 2x+y= -1」と入力するだけで、方程式を解くだけでなく、円と直線の交点を求めるといった数学的意味が分かるグラフを表示してくれる。# すげー
Google でも、y=3x^2-2x+1 みたいな式を入力すると、グラフ表示をしてくれますが、もっと複雑な式でも処理できます。
「z = sin(x^2+y^2)」と入力すれば、3次元プロットまで… # すげー
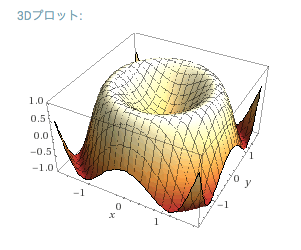
「 integrate 1/x dx 」で不定積分や、「y = diff( x^5+x^3+1 , x ) 」で微分なんてあたりまえ。低学年の数学の授業でグラフ電卓とか使っているけど、その機能以上のことが、スマホでもできてしまう。
「ステップごとの解説」というボタンもあり、数学の授業レベルの解説もしてくれる….とはいえ、これは WolframAlpha Pro の機能で有料。
( (1-cos(t)) cos(t) , sin(t)(1-cos(t)) ) でカージオイド(心臓形)まで表示してくれらぁ。
様々な移動平均・レポート-No.3
移動平均のレポートでは、表計算ソフトを用いて、移動平均の範囲のとり方などを変えながら、平均をとった結果に、どう影響するのかを考える。
Excel で様々な移動平均の式を入力
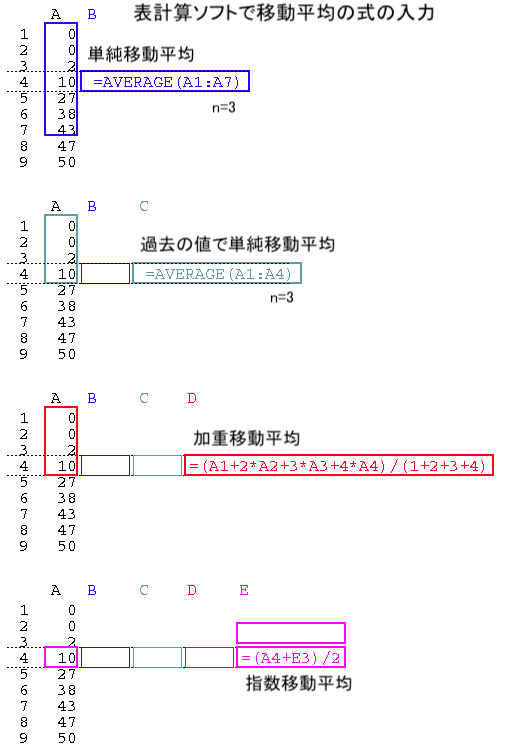
表計算ソフトに、移動平均の式を入力する際には、以下の資料を参考にせよ。
上図のB4〜E4にできた移動平均の式は、B5以下にコピーすればいい。
レポート内容
以下のような移動平均を、Excel にて計算し、その結果の違いについて考察せよ。
移動平均で用いる点の数は、自分の出席番号の3の余りによって、条件を与える。
| 計算方法 | 出席%3=0 | 出席%3=1 | 出席%3=2 |
|---|---|---|---|
| 単純移動平均(狭) | n=3 | n=4 | n=5 |
| 単純移動平均(広) | n=6 | n=8 | n=10 |
| 過去の値による単純移動平均(狭) | n=3 | n=4 | n=5 |
| 過去の値による単純移動平均(広) | n=6 | n=8 | n=10 |
| 加重移動平均(狭) | n=3 | n=4 | n=5 |
| 加重移動平均(広) | n=6 | n=8 | n=10 |
| 指数移動平均(基本) | α=1/2 | α=1/2 | α=1/2 |
| 指数移動平均(広) | α=1/3 | α=1/4 | α=1/5 |
平均に用いる値は、以下のデータとする。
-
- 2018-06-05-wave.csv 時刻tとx(t)のコンマ区切りファイル
- 時間の遅延がわかるような波形を用い、考察してあることが望ましい
1枚のグラフの中に、元波形+8波形=9本のグラフを記載すると、グラフの内容が分かりにくいので、複数のグラフ結果で図示すること。
プログラミングが得意な人は、上記をExcelで処理するのではなく、C言語にて移動平均を計算し、結果をExcelに取り込んでグラフとして表示することにチャレンジしてほしい。
提出レポートに、全データの計算結果は不要です。動作の確認の意味で、先頭10点ほどの計算結果をつけてください。
様々な移動平均
波形処理をハードウェアで行うかソフトウェアで行うか
組込み用の小型コンピュータが普及する以前は、このような波形に対する処理を行う場合には、電子回路的に波形のフィルタリングを行っていた。しかし電子回路的な方法では、回路の特性が変化してうまく処理ができなくなった場合に、回路の組み換えが発生するかもしれない。ただし回路の変更は基板の作り直しが必要であったりすることから、コストがかかる。
一方、A/D変換機能を内蔵した組込み用小型コンピュータも極めて安価になってきた。
こういったコンピュータの普及で、最近ではアナログ値をコンピュータに取り込んでデジタルの数値的な処理で余計な情報を取り除く。この方法であれば、プログラムを変更するだけなので、安価に変更が可能となる。ただし、アナログ値をA/D変換するのには時間がかかることから、周波数の高い信号には不向きである。
単純移動平均
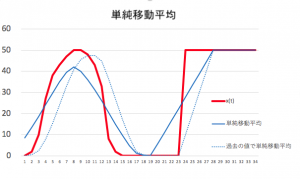
前回説明を行った単純移動平均は、時刻tの平均を、その前後のデータで平均を求めた。この方式は、実際には与えられた波形のデータを全部記録した跡に、単純移動平均をとる場合に有効である。
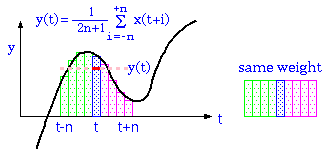
しかし、時々刻々変化する測定値の平均をその都度使うことを考えると、上記の方法は、未来の測定値
を使っていることから、現実的ではない。
#define NS 3
int x[ SIZE ] ; // 入力値
int y[ SIZE ] ; // 出力値
for( int t = NS ; t < SIZE-NS ; t++ ) {
int s = 0 ;
for( int i = -NS ; i <= +NS ; i++ ) // 2*NS+1回の繰り返し
s += x[t+i] ;
y[t] = s / (2*NS + 1) ;
}
過去の値だけを使った移動平均
そこで、過去の値だけで移動平均をとることも考えられる。
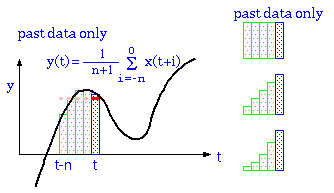
この、単純移動平均と、過去の値だけを使う単純移動平均を、適当な測定値に対して適用した場合のグラフの変化を Excel によってシミュレーションした結果を以下に示す。
しかし、このグラフを見ると、波形後半の部分に注目するとよく分かるが、過去の値だけを使った移動平均では、測定値が立ち上がったのを追いかけて値が増えていく。これでは移動平均は時間的な遅れとなってしまう。
for( int t = NS ; t < SIZE ; t++ ) {
int s = 0 ;
for( int i = 0 ; i <= NS ; i++ ) // NS+1回の繰り返し
s += x[t-i] ;
y[t] = s / (NS+1) ;
}
加重移動平均
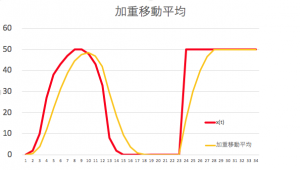
過去の値を使った移動平均では遅れが発生する。でも、平均を取る際に、「n回前の値」と「現在の値」を考えた時、「その瞬間の平均値」は「現在の値」の方が近い値のはず。であれば、平均を取る時に、「n回前の値は少なめ」「現在の値は多め」に比重をかけて加算する方法がある。
for( int t = 3 ; t < SIZE ; t++ ) {
int s = x[t] * 3
+ x[t-1] * 2
+ x[t-2] * 1 ; // 数個の移動平均だし、
y[t] = s / (3+2+1) ; // ループを使わずに書いてみる。
}
この様に、過去に遡るにつれ、平均をとる比重を直線的に小さくしながら移動平均をとる方法は、加重移動平均と呼ばれる。以下にその変化をExcelでシミュレーションしたものを示す。
指数移動平均
ここまで説明してきた、単純移動平均や、加重移動平均は、平均をとる範囲の「過去の値」を記憶しておく必要がある。広い時間にわたる移動平均をとる場合は、それに応じてメモリも必要となる。これは、組み込み型の小型コンピュータであれば、メモリが足りず平均処理ができない場合もでてくる。
そこで、荷重移動平均の重みを、は、100%,
は50%,
は25%… というように、過去に遡るにつれ、半分にして平均をとる。
しかし、以降の項で、
を使うと以下のように書き換えることができる。
for( int t = 1 ; t < SIZE ; t++ ) {
y[t] = ( x[t] + y[t-1] ) / 2 ;
}
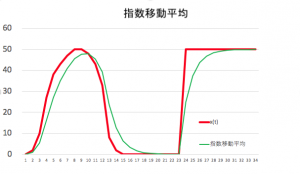
この方法であれば、直前の平均値を記録しておくだけで良い。このような移動平均を、指数移動平均と呼ぶ。
ここで示した指数移動平均は、過去を遡るにつれとなっているが、これをさらに一般化した指数移動平均は、以下の式で示される。前述の移動平均は、
とみなすことができる。
#define ALPHA 0.5
for( int t = 1 ; t < SIZE ; t++ ) {
y[t] = ALPHA * x[t] + (1.0 - ALPHA) * y[t-1] ;
}
以下のプログラムは、うまく動かない。理由を説明せよ。
#define RVA 4 for( int t = 1 ; t < SIZE ; t++ ) { // 以下はy[t]は全部ゼロになる。 y[t] = 1/RVA * x[t] + (1.0 - 1/RVA) * y[t-1] ; // 以下は、整数型演算だけで、正しく動くだろう。 // y[t] = ( x[t] + (RVA-1) * y[t-1] ) / RVA ; }
K-SEC セキュリティサマースクールin 岐阜高専
夏休みに開催される、高専学生対象のセキュリティに関するサマースクールのお知らせです。
- 期日 平成30年8月23日(木)・24日(金)
- 会場 岐阜工業高等専門学校 専攻科棟2 階 第1講義室・第2講義室
- 内容
学生の情報セキュリティに関する知識とスキルの向上と、情報セキュリティ教育に関わる教員の研鑽を目的として、2日間で情報セキュリティ高度人材育成に関するサマースクールを実施する。
1日目【8月23日(木)】
09:30 – 10:00 受付
10:10 – 10:20 挨拶
10:30 – 12:00 講座A/講座B
12:00 – 13:00 昼休み
13:00 – 14:30 講座C/講座D
14:40 – 16:10 講座E/講座F2日目【8月24日(金)】
08:30 – 08:45 受付
08:50 – 10:20 講座G/講座H
10:30 – 12:00 講座I/講座J
12:10 – 12:40 クロージング - 参加対象学生
各国公私立高等専門学校の本科学生および専攻科生(定員:40 名)
- 見学対象教職員
全国各校の情報セキュリティ教育担当者、または情報セキュリティ教育にご興味のある方
福井高専の参加希望者は、6/29までに斉藤に連絡をください。
高専プロコン連携シンポジウム2018の開催について
高専プロコンを前に、現場のニーズや動向を学習する機会を提供することを目的としたシンポジウムがテレビ会議システムにて開催されます。電子情報工学科の皆様および高専プロコンに興味のある方は、ぜひ参加をお願いします。
- 概 要
全国高専を結んだビデオ会議システムにより,講師から企業,高専生,プロコンの関係についての情報を提供頂きます。プロコンに興味を持っている教職員及び学生はもちろん,一般の学生にも興味の持てる内容となっております。 - 日 程
平成30年6月22日(金)16:20~17:20
福井高専合併教室(石川高専から配信) - 講演者・講演タイトル
16時20分~16時50分
講 師:チームラボ株式会社 取締役 CTO 田村 哲也 様
講演テーマ:会社が求める人材と高専プロコン
16時50分~17時20分
講 師:合同会社DMM.com 動画配信開発部 矢野完人 様
講演テーマ:高専生がITベンチャーで働くって? - 参加方法
質疑応答は,Twitterを利用予定です(質問はハッシュタグ #procon29 でお寄せください)。 - その他
追加情報等につきましては,プロコン公式サイト(http//www.procon.gr.jp/)及びメールにてご連絡いたします。
(2018-06-22)
プロコンシンポジウムでは、電子情報4年から、10名の学生さんが参加・聴講してくれました。
動画配信では、多くの利用者が集中したためか、上流の動画配信サーバからの配信で聞きづらい状態でした。その中でも、Twitter でいろいろな感想が飛び交っていました。
Googleスピードテスト
ブラウザを用いた Google によるインターネット速度テストの結果。
自宅、500Mbps超えてたのに比べたら…(x_x;