移動平均の処理
前回の授業で説明したようなA/D変換した数値データを読み取った場合、どのようなことが発生するか考える。
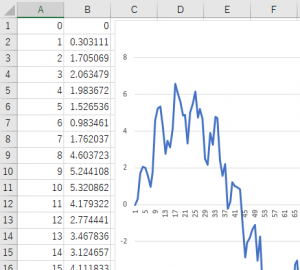
例えば、以下に示すような測定値があったとする。
このデータの一部をグラフ化してみると、次のような波形であった。
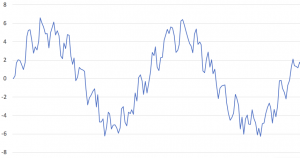
この波形をみると、大きく見ればsinカーブだが、細かい点を見るとデータにブレがある。
誤差の原因
このような測定結果が得られた場合、本来コンピュータで処理したいデータは何であろうか?
原因は様々なものが考えられるが、
(1) 回路のノイズ対策が不十分で、外部の電気的な影響が混入してしまうこともある。
(2) 一方で、D/A 変換を行う場合には、量子化誤差もある。
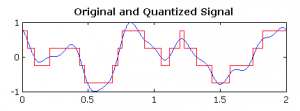
青線:元波形、赤線:4段階で量子化
この例は、-1〜1の範囲を、4段階に量子化することで、本来の波形とは異なった値になっている。
例えば、最初の波形が、加速度センサーの値であったとして、船の上で揺れているために、大きな周期で加速度が変化しているかもしれない。一方で、船自体がエンジンによる揺れで加速度が変化しているかもしれない。
船の中で波の揺れと、エンジンの揺れが観測されている加速度センサーの情報で、船の揺れの大きさ・揺れの周期を知りたい場合、どうすればいいだろうか?単純なsinカーブの波形であれば、波形の最大値・最小値・0との交点の場所を探せば、振幅や周期が求めることができるが、このようなノイズが入った波形では、正しく振幅・周期が求まらない。
移動平均
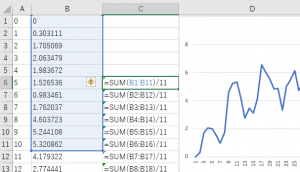
このデータを見ると、10個のデータまでの間で、波形が上下に変動している。船の揺れとエンジンの揺れが原因であれば、10個ぐらいのデータのゆらぎが、エンジンによる揺れと考えられる。では、この10個ぐらいの範囲で値が上下の影響を減らしたければ、どうすればいいか?一番簡単な方法は、前後10個のデータで平均を取ればいいだろう。まずは、Excel で前後データの平均をとってみよう。
Excelで前後11点の平均を求める式をセルに入れる
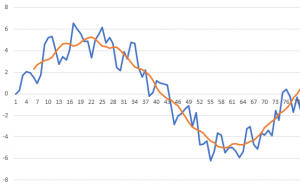
青線:元波形データ(B列)、赤線:前後11点の平均(C列)
このように、データの前後の決められた範囲の平均を平均する処理は、移動平均(単純移動平均)と呼ぶ。
時間tにおけるデータをとした場合、前後5点の移動平均
は、以下のような式で表せるだろう。
自宅学習の課題(レポート提出は不要)
表計算ソフトで、移動平均を計算させてみよう。 ※
- 元波形
- 前後5点で移動平均
- 前後11点で移動平均
- 前後51点で移動平均
をとるような表計算の式を書き込んで、その結果の波形がどんなグラフになるのか確認しておくこと。
移動平均の応用
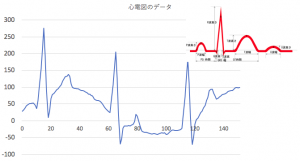
例えば、以下のような心電図のデータがあったとする。心電図では、波の高さで心臓が正常か判断するが、この青のグラフでは、大きな周期の変動が含まれるため、波の高さを正確に測れない。この波形から診断するときに、移動平均が使えないだろうか?
このような場合には、測定値の波形の移動平均をとり心拍データの変動を取り除き、測定値から移動平均の値を引くことで、心拍データだけを取り出すことが可能となる。