前回の授業では、簡単な再帰呼び出しのプログラムについて再帰方程式などの説明を行った。今日の授業では、ハノイの塔の処理時間や、マージソートのプログラムの処理時間について検討を行う。

ハノイの塔

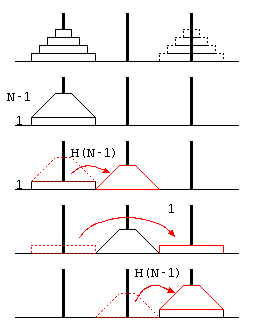ハノイの塔は、３本の塔にN枚のディスクを積み、(1)1回の移動ではディスクを1枚しか動かせない、(2)ディスクの上により大きいディスクを積まない…という条件で、山積みのディスクを目的の山に移動させるパズル。

一般解の予想

ハノイの塔の移動回数を とした場合、 少ない枚数での回数の考察から、 以下の一般式で表せることが予想できる。

 … ①

この予想が常に正しいことを証明するために、ハノイの塔の処理を、 最も下のディスク1枚への操作と、その上の(N-1)枚のディスクへの操作に分けて考える。

再帰方程式

上記右の図より、N枚の移動をするためには、上に重なるN-1枚を移動させる必要があるので、

 … ②
　… ③

ということが言える。(これがハノイの塔の移動回数の再帰方程式)
ディスクが枚の時、予想が正しいのは明らか①,②。
ディスクが 枚で、予想が正しいと仮定すると、 枚では、

　… ③より
 … ①を代入

となり、 枚でも、予想が正しいことが証明された。 よって数学的帰納法により、1枚以上で予想が常に成り立つことが証明できた。

理解度確認

• 前再帰の「ピラミッドの体積」pyra() を、ループにより計算するプログラムを記述せよ。
• 前講義での2分探索法のプログラムを、再帰によって記述せよ。(以下のプログラムを参考に)。また、このプログラムの処理時間にふさわしい再帰方程式を示せ。

int a[ 10 ] = {
   7 , 12 , 22 , 34 , 41 , 56 , 62 , 78 , 81 , 98
} ;
int find( int array[] , int L , int R , int key ) { // 末尾再帰
   // 目的のデータが見つかったら 1,見つからなかったら 0 を返す。
   if ( __________ ) {
      return ____ ; // 見つからなかった
   } else {
      int M = _________ ;
      if ( array[ M ] == key )
         return ____ ;
      else if ( array[ M ] > key )
         return find( array , ___ , ___ , key ) ;
      else
         return find( _____ , ___ , ___ , ___ ) ;
   }
}
int main() {
   if ( find( a , 0 , 10 , 56 ) )
      printf( "みつけた¥n" ) ;
}

再帰を使ったソートアルゴリズムの分析

データを並び替える有名なアルゴリズムの処理時間のオーダは、以下の様になる。

• バブルソート
• 選択法
  ※本来は1/2は比例定数なのでオーダの中には書かない。ただし比較計算量がバブルソートの半分であることを強調する時は、この様に書くことが多い。
• クイックソート
• マージソート
  • 参考：ソートアルゴリズム12種を可視化してみた

この中で、高速なソートアルゴリズムは、クイックソート(最速のアルゴリズム)とマージソート(オーダでは同程度だが若干効率が悪い)であるが、ここでは、再帰方程式で処理時間をイメージしやすい、マージソートにて説明を行う。

マージソートの分析

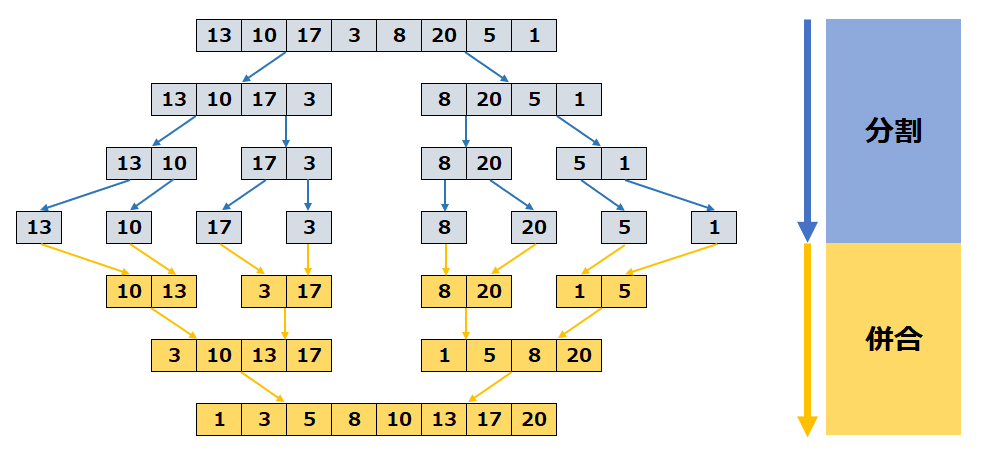
マージソートは、与えられたデータを2分割し、 その2つの山をそれぞれマージソートを行う。 この結果の2つの山の頂上から、大きい方を取り出す…という処理を繰り返すことで、 ソートを行う。

• 参考: マージソート(併合整列法)

このことから、再帰方程式は、以下のようになる。

• 
• 

この再帰方程式を、N=1,2,4,8…と代入を繰り返していくと、 最終的に処理時間のオーダが となる。

：

よって、処理時間のオーダは  となる。

選択法とクイックソートの処理時間の比較

データ数 N = 20 件でソート処理の時間を計測したら、選択法で 10msec 、クイックソートで 20msec であった。

1. データ件数 N = 100 件では、選択法,クイックソートは、それぞれどの程度の時間がかかるか答えよ。
2. データ件数何件以上なら、クイックソートの方が高速になるか答えよ。

設問2 は、通常の関数電卓では求まらないので、数値的に方程式を解く機能を持った電卓などが必要。[解説]