スタックと待ち行列
前回の授業では、リストの先頭にデータを挿入する処理と、末尾に追加する処理について説明したが、この応用について説明する。
計算処理中に一時的なデータの保存として、スタック(stack)と待ち行列・キュー(queue)がよく利用される。それを配列を使って記述したり、任意の大きさにできるリストを用いて記述することを示す。
スタック
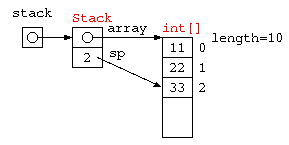
配列を用いたスタック
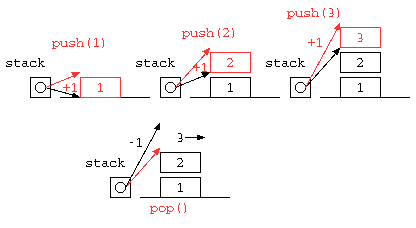
一時的な値の記憶によく利用されるスタック(stack)は、データの覚え方の特徴からLIFO( Last In First out )とも呼ばれる。配列を使って記述すると以下のようになるであろう。
import java.util.*;
public class Main {
static final int STACK_SIZE = 10 ;
static int[] stack = new int[ STACK_SIZE ] ;
static int sp = 0 ;
static void push( int x ) {
stack[ sp++ ] = x ;
}
static int pop() {
return stack[ --sp ] ;
}
public static void main(String[] args) throws Exception {
push( 11 ) ;
push( 22 ) ;
push( 33 ) ;
System.out.println( pop() ) ;
System.out.println( pop() ) ;
System.out.println( pop() ) ;
}
}
配列を使った Stack をオブジェクト指向で記述するなら、以下のように書ける。
import java.util.*;
class Stack {
static final int STACK_SIZE = 10 ;
int[] array ;
int sp ;
Stack() {
this.array = new int[ STACK_SIZE ] ;
this.sp = 0 ;
}
void push( int x ) {
array[ sp++ ] = x ;
}
int pop() {
return array[ --sp ] ;
}
} ;
public class Main {
public static void main(String[] args) throws Exception {
Stack stack = new Stack() ;
stack.push( 11 ) ;
stack.push( 22 ) ;
stack.push( 33 ) ;
System.out.println( stack.pop() ) ;
System.out.println( stack.pop() ) ;
System.out.println( stack.pop() ) ;
}
}
C言語で書いた場合
#define STACK_SIZE 32
int stack[ STACK_SIZE ] ;
int sp = 0 ;
void push( int x ) { // データをスタックの一番上に積む
stack[ sp++ ] = x ;
}
int pop() { // スタックの一番うえのデータを取り出す
return stack[ --sp ] ;
}
void main() {
push( 1 ) ; push( 2 ) ; push( 3 ) ;
printf( "%d\n" , pop() ) ; // 3
printf( "%d\n" , pop() ) ; // 2
printf( "%d\n" , pop() ) ; // 1
}

++,–の前置型と後置型の違い
// 後置インクリメント演算子 int i = 100 ; printf( "%d" , i++ ) ; // これは、 printf( "%d" , i ) ; i++ ; // と同じ。100が表示された後、101になる。 // 前置インクリメント演算子 int i = 100 ; printf( "%d" , ++i ) ; // これは、 i++ ; printf( "%d" , i ) ; // と同じ。101になった後、101を表示。
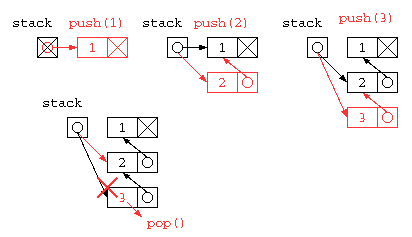
リスト構造を用いたスタック
しかし、この中にSTACK_SIZE以上のデータは貯えられない。同じ処理をリストを使って記述すれば、配列サイズの上限を気にすることなく使うことができるだろう。では、リスト構造を使ってスタックの処理を記述してみる。
import java.util.*;
class ListNode {
int data ;
ListNode next ;
ListNode( int d , ListNode n ) {
this.data = d ;
this.next = n ;
}
}
public class Main {
static ListNode stack = null ;
static void push( int x ) {
stack = new ListNode( x , stack ) ;
}
static int pop() {
int ans = stack.data ;
stack = stack.next ;
return ans ;
}
public static void main(String[] args) throws Exception {
push( 1 ) ;
push( 2 ) ;
push( 3 ) ;
System.out.println( pop() ) ;
System.out.println( pop() ) ;
System.out.println( pop() ) ;
}
}
struct List* stack = NULL ;
void push( int x ) { // リスト先頭に挿入
stack = cons( x , stack ) ;
}
int pop() { // リスト先頭を取り出す
int ans = stack->data ;
struct List* d = stack ;
stack = stack->next ; // データ 0 件で pop() した場合のエラー対策は省略
free( d ) ;
return ans ;
}
オブジェクト指向っぽく書くならば、下記のようになるだろう。初期状態で stack = null にしておくと、stack.push() ができないので、stack の先頭には、ダミーデータを入れるようにプログラムを書くと以下のようになるだろう。
import java.util.*;
class ListNode {
int data ;
ListNode next ;
ListNode( int d , ListNode n ) {
this.data = d ;
this.next = n ;
}
ListNode() { // stack初期化用のコンストラクタ
this.data = -1 ;
this.next = null ;
}
void push( int x ) {
this.next = new ListNode( x , this.next ) ;
}
int pop() {
int ans = this.next.data ;
this.next = this.next.next ;
return ans ;
}
} ;
public class Main {
public static void main(String[] args) throws Exception {
ListNode stack = new ListNode() ; // stack初期化用のコンストラクタを使う
stack.push( 1 ) ;
stack.push( 2 ) ;
System.out.println( stack.pop() ) ;
System.out.println( stack.pop() ) ;
}
}
キュー(QUEUE)
2つの処理の間でデータを受け渡す際に、その間に入って一時的にデータを蓄えるためには、待ち行列(キュー:queue)がよく利用される。 データの覚え方の特徴からFIFO(First In First Out)とも呼ばれる。
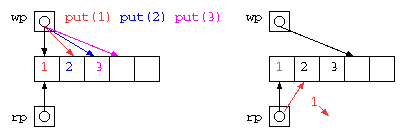
配列を用いたQUEUE / リングバッファ
配列にデータを入れる場所(wp)と取り出す場所のポインタ(rp)を使って蓄えれば良いが、配列サイズを超えることができないので、データを取り出したあとの場所を循環して用いるリングバッファは以下のようなコードで示される。
import java.util.*;
public class Main {
static final int QUEUE_SIZE = 32 ;
static int[] queue = new int[ QUEUE_SIZE ] ;
static int wp = 0 ;
static int rp = 0 ;
static void put( int x ) {
queue[ wp++ ] = x ;
if ( wp >= QUEUE_SIZE ) // wp = wp % QUEUE_SIZE ; or wp = wp & (QUEUE_SIZE - 1) ;
wp = 0 ;
}
static int get() {
int ans = queue[ rp++ ] ;
if ( rp >= QUEUE_SIZE ) // rp = rp % QUEUE_SIZE ; or rp = rp & (QUEUE_SIZE - 1) ;
rp = 0 ;
return ans ;
}
public static void main(String[] args) throws Exception {
// Your code here!
put( 1 ) ;
put( 2 ) ;
put( 3 ) ;
System.out.println( get() ) ;
System.out.println( get() ) ;
System.out.println( get() ) ;
}
}
#define QUEUE_SIZE 32
int queue[ QUEUE_SIZE ] ;
int wp = 0 ; // write pointer(書き込み用)
int rp = 0 ; // read pointer(読み出し用)
void put( int x ) { // 書き込んで後ろ(次)に移動
queue[ wp++ ] = x ;
if ( wp >= QUEUE_SIZE ) // 末尾なら先頭に戻る
wp = 0 ;
}
int get() { // 読み出して後ろ(次)に移動
int ans = queue[ rp++ ] ;
if ( rp >= QUEUE_SIZE ) // 末尾なら先頭に戻る
rp = 0 ;
return ans ;
}
void main() {
put( 1 ) ; put( 2 ) ; put( 3 ) ;
printf( "%d\n" , get() ) ; // 1
printf( "%d\n" , get() ) ; // 2
printf( "%d\n" , get() ) ; // 3
}

このようなデータ構造も、get() の実行が滞るようであれば、wp が rp に循環して追いついてしまう。このため、上記コードはまだエラー対策としては不十分である。どのようにすべきか?
リスト構造を用いたQUEUE
前述のリングバッファもget()しないまま、配列上限を越えてput()を続けることはできない。
この配列サイズの上限問題を解決したいのであれば、リスト構造を使って解決することもできる。この場合のプログラムは、以下のようになるだろう。
import java.util.*;
class ListNode {
int data ;
ListNode next ;
ListNode( int d , ListNode n ) {
this.data = d ;
this.next = n ;
}
} ;
public class Main {
static ListNode top = new ListNode( -1 , null ) ;
static ListNode tail = top ;
static void put( int x ) {
tail.next = new ListNode( x , null ) ;
tail = tail.next ;
}
static int get() {
int ans = top.next.data ;
top.next = top.next.next ;
return ans ;
}
public static void main(String[] args) throws Exception {
put( 1 ) ;
put( 2 ) ;
put( 3 ) ;
System.out.println( get() ) ;
System.out.println( get() ) ;
System.out.println( get() ) ;
}
}
Javaで書かれた ListNode を用いた待ち行列のイメージ図は下記のように示される。
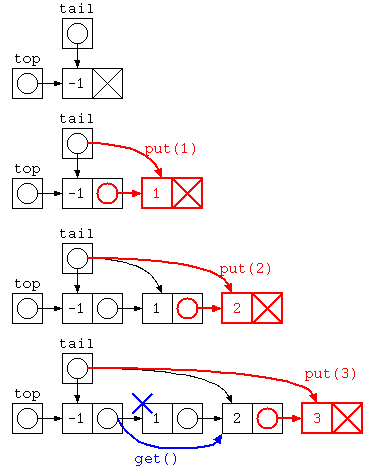
struct List* queue = NULL ;
struct List** tail = &queue ;
void put( int x ) { // リスト末尾に追加
*tail = cons( x , NULL ) ;
tail = &( (*tail)->next ) ;
}
int get() { // リスト先頭から取り出す
int ans = queue->data ;
struct List* d = queue ;
queue = queue->next ;
free( d ) ;
return ans ;
}
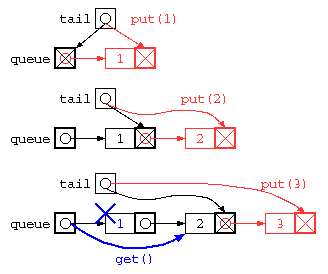
ただし、上記のプログラムは、データ格納後にget()で全データを取り出してしまうと、tail ポインタが正しい位置になっていないため、おかしな状態になってしまう。
また、このプログラムでは、rp,wp の2つのポインタで管理することになるが、 2重管理を防ぐために、リストの先頭と末尾を1つのセルで管理する循環リストが使われることが多い。
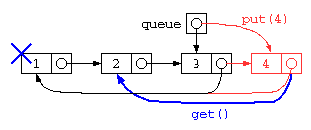
理解確認
- 配列を用いたスタック・待ち行列は、どのような処理か?図などを用いて説明せよ。
- リスト構造を用いたスタック・待ち行列について、図などを用いて説明せよ。
- スタックや待ち行列を、配列でなくリスト構造を用いることで、どういう利点があるか?欠点があるか説明せよ。
- 配列を用いたリングバッファが用いられている身近な例にはどのようなものがあるか?
- 配列を用いたリングバッファを実装する場合配列サイズには 2n 個を用いることが多いのはなぜだろうか?
リスト処理のレポート課題(前期期末)
プログラムは書いて・動かして・間違って・直す が重要ということで、以下に前期期末試験前までに取り組むレポート課題をしめす。
レポート課題(プログラム例)
Java を用いて、後に示すデータ処理をするためのリスト構造を定義し、与えられたデータを追加していく処理を作成せよ。
課題の説明用に、複素数のリスト構造を定義し、指定した絶対値以下の複素数を抜き出す関数をつくった例を示す。
import java.util.* ;
class ComplexListNode {
double re ;
double im ;
ComplexListNode next ;
ComplexListNode( double r , double i , ComplexListNode n ) {
this.re = r ;
this.im = i ;
this.next = n ;
}
} ;
public class Main {
// 先頭からデータを挿入する方式
static ComplexListNode top = null ;
// 全リストを表示する処理
static void print( ComplexListNode p ) {
for( ; p != null ; p = p.next ) {
System.out.println( "(" + p.re + ")+j(" + p.im + ")" ) ;
}
}
// top に要素を追加する処理(先頭に入れる)
static void add( double r , double i ) {
top = new ComplexListNode( r , i , top ) ;
}
// 特定のデータを対象にした処理の例
static ComplexListNode filter_lessthan( ComplexListNode p , double v_abs ) {
ComplexListNode ans = null ;
for( ; p != null ; p = p.next ) {
if ( Math.sqrt( p.re * p.re + p.im * p.im ) <= v_abs )
ans = new ComplexListNode( p.re , p.im , ans ) ;
}
return ans ;
}
public static void main(String[] args) throws Exception {
add( 1.0 , 2.0 ) ;
add( -1.0 , -1.0 ) ;
add( 2.0 , -1.0 ) ;
add( 1.0 , 0 ) ;
print( top ) ;
ComplexListNode less_than_2 = filter_lessthan( top , 2 ) ;
System.out.println( "less than 2" ) ;
print( less_than_2 ) ;
}
}
((( 実行結果の例 )))
(1.0)+j(0.0)
(2.0)+j(-1.0)
(-1.0)+j(-1.0)
(1.0)+j(2.0)
less than 2
(-1.0)+j(-1.0)
(1.0)+j(0.0)
レポート内容
上記のプログラムをまねて、以下のレポート課題を作成すること。テーマは ((出席番号-1)%3+1) を選択すること。
- 年号のデータが、年号の名称と年号の始まりの年月日がYYYYMMDD形式で
- “Meiji”,18681023
- “Taisho”,19120730
- “Showa”,19261225
- “Heisei”,19890108
- “Reiwa”,20190501
の様に与えられる。このデータ構造を覚えるリスト構造を作成せよ。また ListNode のデータで、西暦の日付のリストが seireki_list = new ListNode( 19650207, new ListNode( 20030903 , null ) ) ; のように与えられたら、そのデータを和暦で表示するプログラムを作成せよ。 (参考2023年前期期末)
- 市町村名,月,日,最高気温,最低気温のデータが、
- “fukui”,8月,4日,27.6℃,22.3℃
- “fukui”,8月,5日,31.5℃,23.3℃
- “fukui”,8月,7日,34.7℃,25.9℃
- “obama”,8月,6日,34.2℃,23.9℃
の様に与えられる。このデータ構造で覚えるリスト構造を作成せよ。また、この中から真夏日(最高気温が30℃以上)でかつ熱帯夜(最低気温が25℃以上)の日のリストを抽出し表示するプログラムを作成せよ。(参考2022年前期期末)
- ホスト名と、IPアドレス(0~255までの8bitの値✕4個で与えるものとする)のデータ構造で、
- “www.fukui-nct.ac.jp”,104,215,54,205
- “perrine.tsaitoh.net”,192,168,11,2
- “dns.fukui-nct.ac.jp”,10,10,21,51
- “dns.google.com”,8,8,8,8
の様に与えられる。このデータ構造をリスト構造で覚えるプログラムを作成せよ。また、この中からプライベートアドレスのリストを抽出し表示するプログラムを作成せよ。プライベートアドレスは 10.x.x.x, 172.16~31.x.x,192.168.x.x とする。(参考2019年前期期末)
プログラムを作るにあたり、リスト構造には add( 与えられたデータ… ) のように呼び出してリストに追加すること。この時、生成されるリストが、登録の逆順になるか(先頭に挿入)、登録順(末尾に追加)になるかは、自分の理解度に応じて選択すること。抽出する処理を書く場合も登録順序どおりにするかは自分の理解度に応じて選べばよい。
また、理解度に自信がある人は、add() などの処理を「オブジェクト指向」のように記述する方法を検討すること。
あくまで、リスト構造の理解を目的とするため、ArrayList<型> , LinkedList<型> のようなクラスは使わないこと。(ただし考察にて記述性の対比の対象として使うのはOK。複素数の場合の LinkedList を使った例を以下に示す。)
import java.util.* ;
import java.util.stream.Collectors ;
class Complex {
double re ;
double im ;
Complex( double r , double i ) {
this.re = r ;
this.im = i ;
}
public double abs() {
return Math.sqrt( re * re + im * im ) ;
}
@Override
public String toString() {
return "(" + re + ")+j(" + im + ")" ;
}
} ;
public class Main {
public static LinkedList<Complex> top = new LinkedList<Complex>() ;
// 絶対値が指定した値以下の要素だけを集める関数
public static LinkedList<Complex> filter_lessthan(
LinkedList<Complex> list , double v_abs ) {
var ans = new LinkedList() ;
for( var c : list ) {
if ( Math.sqrt( c.re * c.re + c.im * c.im ) <= v_abs )
ans.add( c ) ;
}
return ans ;
}
public static void main( String[] args ) throws Exception {
// リストに複素数を追加
top.add( new Complex( 1.0 , 2.0 ) ) ;
top.add( new Complex( -1.0 , -1.0 ) ) ;
top.add( new Complex( 2.0 , -1.0 ) ) ;
top.add( new Complex( 1.0 , 0 ) ) ;
for( var c : top ) {
System.out.println( c ) ;
}
System.out.println( "---" ) ;
// static な関数でフィルタリング
for( var c : filter_lessthan( top , 2.0 ) ) {
System.out.println( c ) ;
}
/* Stream API を使ってフィルタリング
for( var c : top.stream() // LinkedList を Stream に変換
.filter( c->c.abs() < 2.0 ) // filter条件をラムダ式で渡す
.collect( Collectors.toList() ) // Collectorsで結果を集める
) {
System.out.println( c ) ;
}
*/
}
}
- LinkedListを使ったプログラム例(Paiza.io)
Javaでリスト構造
テスト前のリスト導入の復習
前回のリスト構造の導入では、配列のデータに次のデータの入っている番号を添えることで途中にデータを挿入できるデータ構造の説明をした。
ヒープメモリとは
Javaでは、すべてのオブジェクトはヒープメモリに保存する。
ヒープメモリとは、一時的なデータの保管場所であり、new 演算子でデータを保存する場所を確保する。
Javaでは、分かり難いのでC言語で説明を行う。malloc() は、指定されたバイト数のメモリをヒープ領域に確保する命令。malloc() に失敗すると、NULL が返ってくる。また、使い終わったら malloc() の領域は free() 命令で返却が必要となる。
((( 配列をヒープメモリで確保 )))
#include <stdio.h>
#include <stdlib.h>
int main() {
int a[ 5 ] = { 1 , 2 , 3 , 4 , 5 } ;
int* b ;
if ( (b = (int*)malloc( sizeof( int ) * 5 )) != NULL ) {
for( int i = 0 ; i < 5 ; i++ )
b[ i ] = i + 1 ;
free( b ) ; // malloc() で確保したメモリ領域は返却が必要
}
return 0 ;
}
((( オブジェクトをヒープメモリに確保 )))
struct Complex {
double re ;
double im ;
} ;
int main() {
struct Complex* c ;
if ( (c = (struct Complex*)malloc( sizeof( struct Complex ) )) != NULL ) {
c->re = 1.23 ;
c->im = 2.34 ;
free( c ) ;
return 0 ;
} else {
printf( "No heap memory\n" ) ;
return 1 ;
}
}
((( 上記C言語をJavaで書くと )))
class Complex {
double re ;
double im ;
Complex( double r , double i ) {
this.re = r ;
this.im = i ;
}
}
public class Main {
public static void main( String[] args ) {
try {
Complex c = new Complex( 1.23 , 2.34 ) ;
// Javaではヒープメモリが確保に失敗したら、
// OutOfMemoryErrorの例外が発生する。
c = null ; // free()はJavaでは不要
// nullを代入してもいい。
} catch( OutOfMemoryError e ) {
System.out.println( "No heap memory" ) ;
System.exit( 1 ) ;
}
}
}
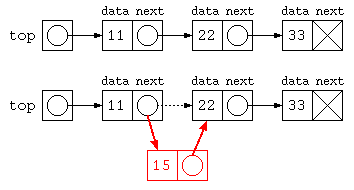
リスト構造 ListNode
前述の data と next で次々とデータを続けて保存する方法を、next の部分を次のデータへの参照を用いるように、リスト構造(連結リスト)を定義する。
import java.util.*;
class ListNode {
int data ; // データ部分
ListNode next ; // 次のデータへの参照
// コンストラクタ
ListNode( int d , ListNode nx ) {
this.data = d ;
this.next = nx ;
}
} ;
public class Main {
public static void main(String[] args) throws Exception {
ListNode top = new ListNode( 11 , new ListNode( 22 , new ListNode( 33 , null ) ) ) ;
for( ListNode p = top ; p != null ; p = p.next )
System.out.println( p.data ) ;
// 途中にデータを入れる
top.next = new ListNode( 15 , top.next ) ;
for( ListNode p = top ; p != null ; p = p.next )
System.out.println( p.data ) ;
}
}
リスト操作
リスト構造に慣れるために簡単な練習をしてみよう。リスト構造のデータに対するメソッドをいくつか作ってみよう。print() や sum() を参考に、データ数を求める count() , 最大値を求める max() , データを検索する find() を完成させてみよう。
class ListNode {
(略)
} ;
public class Main {
static void print( ListNode p ) { // リストを表示
for( ; p != null ; p = p.next )
System.out.print( p.data + " " ) ;
System.out.println() ;
}
static int sum( ListNode p ) { // リストの合計を求める
int s = 0 ;
for( ; p != null ; p = p.next )
s += p.data ;
return s ;
}
static int count( ListNode p ) { // データ件数を数える
}
static int max( ListNode p ) { // データの最大値を求める
}
static boolean find( ListNode p , int key ) { // データ列の中から特定のデータを探す
// 見つかったら true , 見つからなければ false
}
public static void main(String[] args) throws Exception {
ListNode top = new ListNode( 11 , new ListNode( 22 , new ListNode( 33 , null ) ) ) ;
print( top ) ;
System.out.println( "合計:" + sum( top ) ) ;
System.out.println( "件数:" + count( top ) ) ;
System.out.println( "最大:" + max( top ) ) ;
System.out.println( "検索:" + (find( top , 22 )
? "みつかった" : "みつからない" ) ) ;
}
}
オブジェクト指向っぽく書いてみる
前述のプログラムでは、print( top ) のように使う static な関数としてプログラムを書いていた。しかし、オブジェクト指向であれば、オブジェクトに対するメソッドだと top.print() のように書きたい。この場合だと、以下のように書くかもしれない。
import java.util.*;
class ListNode {
int data ;
ListNode next ;
ListNode( int d , ListNode n ) {
this.data = d ;
this.next = n ;
}
void print() { // リストの全データを表示
for( ListNode p = this ; p != null ; p = p.next )
System.out.print( p.data + " " ) ;
System.out.println() ;
}
int sum() { // リストの合計を求める
int s = 0 ;
for( ListNode p = this ; p != null ; p = p.next )
s += p.data ;
return s ;
}
} ;
public class Main {
public static void main(String[] args) throws Exception {
ListNode top = new ListNode( 11 , new ListNode( 22 , new ListNode( 33 , null ) ) ) ;
top.print() ;
System.out.println( "合計: " + top.sum() ) ;
ListNode list_empty = null ;
list_empty.print() ; // 実行時エラー java.lang.NullPointerException ぬるぽ!
}
}
しかし、データ件数 0件 に対してメソッドを呼び出せない。
ListNode と List というクラスで書いてみる
ひとつの方法として、リストの先頭だけのデータ構造を宣言する方法もある。
class ListNode {
int data ;
ListNode next ;
ListNode( int d , ListNode n ) {
this.data = d ;
this.next = n ;
}
} ;
class List {
ListNode top ;
List( ListNode p ) {
this.top = p ;
}
void print() {
for( ListNode p = top ; p != null ; p = p.next )
System.out.print( p.data + " " ) ;
System.out.println() ;
}
} ;
public class Main {
public static void main(String[] args) throws Exception {
List list = new List( new ListNode( 11 , new ListNode( 22 , new ListNode( 33 , null ) ) ) ) ;
list.print() ;
List list_empty = new List( null ) ;
list_empty.print() ;
}
}
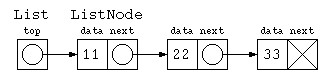
しかし、List と ListNode の2つのデータの型でプログラムを書くのは面倒くさい。
授業ではシンプルに説明したいので、今後はこの方法は極力避けていく。
先頭にダミーデータを入れる
複数のクラス宣言するぐらいなら、リストデータの先頭は必ずダミーにしておく方法もあるだろう。
import java.util.*;
class ListNode {
int data ;
ListNode next ;
ListNode( int d , ListNode n ) {
this.data = d ;
this.next = n ;
}
void print() { // リストの全データを表示
for( ListNode p = this.next ; p != null ; p = p.next )
System.out.print( p.data + " " ) ;
System.out.println() ;
}
} ;
public class Main {
public static void main(String[] args) throws Exception {
ListNode list = new ListNode( -1 , null ) ;
list.next = new ListNode( 11 , new ListNode( 22 , new ListNode( 33 , null ) ) ) ;
top.print() ;
System.out.println( "合計: " + top.sum() ) ;
ListNode list_empty = new ListNode( -1 , null ) ;
list_empty.print() ;
}
}
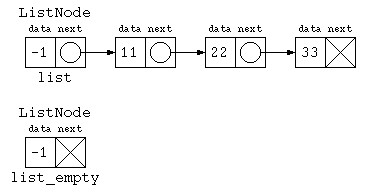
以降、必要に応じて、先頭にダミーを入れる手法も取り混ぜながらプログラムを書くこととする。
入力データをリストに追加
入力しながらデータをリストに格納する処理を考えてみる。
リストでデータを追加保存するのであれば、一番簡単なプログラムは、以下のように先頭にデータを入れていく方法だろう。
class ListNode {
(略)
void print() {
for( ListNode p = this ; p != null ; p = p.next )
System.out.print( p.data ) ;
System.out.println() ;
}
} ;
public class Main {
public static void main(String[] args) throws Exception {
int[] inputs = { 11 , 22 , 33 } ;
ListNode top = null ;
for( int datum : inputs )
top = new ListNode( datum , top ) ;
top.print() ;
}
}
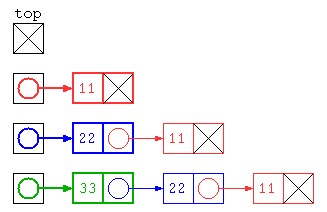
でもこの方法だと、先頭にデータを入れていくため、保存されたデータは逆順になってしまう。
末尾にデータを入れる
逆順になるのを避けるのであれば、データを末尾に追加する方法があるだろう。ただし初期状態でデータが0件だと処理が書きづらいので、先頭にダミーを入れておく方法で書いてみる。
public class Main {
public static void main(String[] args) throws Exception {
int[] test_data = { 11 , 22 , 33 } ;
ListNode top = new ListNode( -1 , null ) ; // ダミー
ListNode tail = top ;
for( int x : test_data ) {
tail.next = new ListNode( x , null ) ;
tail = tail.next ;
}
top.print() ; // -1 11 22 33
} // ダミー
}
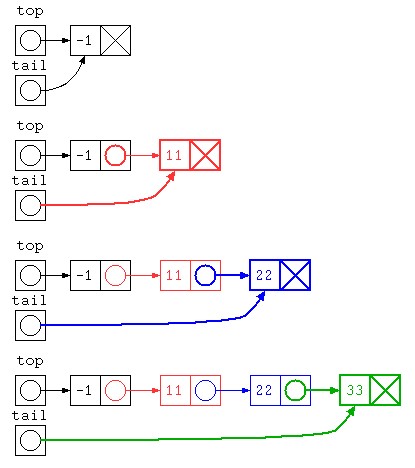
テスト返却と追加説明
前期中間試験の返却に伴い、補足説明。
C言語,Javaにおける文の定義
テストの時に、下記のようなプログラムで piyo() は、for の範囲?みたいな質問があったので、補足説明
for( ... ; ... ; ... )
if ( ... )
foo = bar ;
else {
baz() ;
hoge() ;
}
piyo() ;
C言語やJavaにおける文の定義は、以下の通り
文 ::= 式 ; // 単文
| ; // 空文
| { 文 文 ... } // 複文
| for( .. ; .. ; .. ) 文 // 制御構文
| do 文 while( 式 ) ;
| if ( 式 ) 文 [ else 文 ]
;
こういった文の範囲の誤解を避けるためのものが、インデント。
正しいインデントをつける習慣が重要。
Javaにおけるクラスとデータ構造のイメージ
この後のリスト構造の説明でもオブジェクトがどのように保存されるかを理解するのは重要なので、オブジェクトの説明。
Java では、class 宣言されたデータ構造は、ヒープメモリと呼ばれるデータ領域に保存されている。
class A {
int data ;
A( int value ) {
this.data = value ;
}
} ;
public class Main {
public static void main( String[] args ) {
A a = new A( 123 ) ;
}
}
ここで、new 演算子は、指定されたオブジェクトをヒープメモリ上に確保する。そして、そのデータの入っている領域アドレスを、インスタンスの変数 a に代入している。
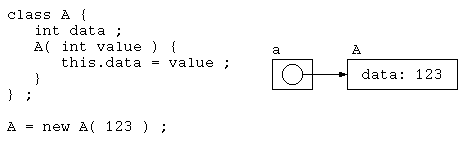
テストで出題した例であれば、
class IdNameAge {
int id ;
String name ;
Age age ;
IdNameAge( int i , String n , int a ) {
this.id = i ;
this.name = n ;
this.age = a ;
}
} ;
IdNameAge[] = people = {
new IdNameAge( 1001 , "saitoh" , 60 ) ,
new IdNameAge( 1002 , "tomoko" , 49 ) ,
new IdNameAge( 1003 , "mitsuki" , 26 ) ,
} ;
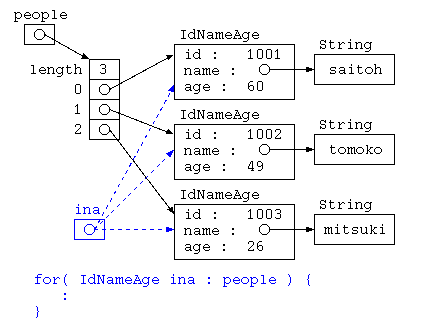
Integer 型も、整数データを記憶するけど、オブジェクト型である。

ただし、Integer 型を常にヒープメモリに保存するのは、効率が悪いので、-128~127までの値ではIntegerオブジェクトは内部でキャッシュされる。Integer y = 123 ; 書いてはいるけど本来であれば、Integer y = new Integer( 123 ) ; と書く必要があった。しかしJava5以降に、オートボクシングと呼ばれる機能があるため Integer y = 123 のように書けるし、こう書く方が推奨されている。
public class Main {
public static void main(String[] args) {
// Your code here!
Integer sx = 123 ;
Integer sy = 123 ;
System.out.println( sx == sy ) ; // true
Integer fx = 12345 ;
Integer fy = 12345 ;
System.out.println( fx == fy ) ; // false
}
}
配列に要素を追加
データが登録済みかどうかを判定する処理を作るために、登録された値を配列に次々と値を追加保存する場合、どのようにプログラムを記述するだろうか?
配列にデータを追加
次々と与えられた値を保存していくのであれば、Java であれば下記のようなコードが一般的であろう。
でも、ArrayList とはどのようにデータを覚えているのだろうか? なぜ 宣言は ArrayList<Integer> array であって ArrayList<int> array で宣言するとエラーが出るのであろうか?
import java.util.*;
public class Main {
public static void main(String[] args) throws Exception {
// ArrayList は連続アドレス空間に保存してくれる可変長配列
// ランダムアクセスをする場合に向いている
ArrayList<Integer> array = new ArrayList<Integer>() ;
array.add( 11 ) ;
array.add( 2 ) ;
array.add( 333 ) ;
for( Integer i : array ) {
System.out.println( i ) ;
}
}
}
このような ArrayList のようなデータ構造の仕組みを考えるために、最も単純な配列でプログラムを作ってみる。
末尾に追加
import java.util.*;
public class Main {
static int[] array = new int[ 10 ] ;
static int size = 0 ;
public static void add( int x ) {
array[ size ] = x ;
size++ ;
}
public static void main(String[] args) throws Exception {
add( 11 ) ;
add( 2 ) ;
add( 333 ) ;
for( int i = 0 ; i < size ; i++ )
System.out.println( array[i] ) ;
}
}
同じ処理をC言語で書いてみる。
#include <stdio.h>
int array[ 10 ] ;
int size = 0 ;
void add( int x ) { // if ( size < array.length ) ... の判定が必要かも
array[ size ] = x ;
size++ ;
}
int main() {
add( 11 ) ;
add( 2 ) ;
add( 333 ) ;
for( int i = 0 ; i < size ; i++ )
printf( "%d\n" , array[ i ] ) ;
return 0 ;
}
しかし、このプログラムでは、最初に宣言した要素数10個を越えてデータを保存できないし、配列溢れさせないためには要素数の上限チェックも必要となるだろう。
昇順に並べながら途中に要素を追加
前述のプログラムでは、配列の末尾の場所を size で覚えておき、末尾にデータを追加していた。でも、配列に保存されている値の中から目的の値が含まれているか検索したいのであれば、配列に要素を昇順に保存しておいて2分探索法を使うのが一般的であろう。では、前述のプログラムを昇順で保存するにはどうすべきか?
最も簡単な方法で書くのであれば、下記のようなコードになるかもしれない。
public static void add( int x ) {
int i ;
for( i = 0 ; i < size ; i++ ) { // ここは2分探索で書けば O( log N ) にできるかも
if ( array[ i ] > x )
break ;
}
// for( int j = i ; j < size ; j++ ) // 途中に挿入は、コレじゃダメ?
// array[ j + 1 ] = array[ j ] ;
for( int j = size - 1 ; j >= i ; j-- ) // 途中にデータを入れるために要素を1つ後ろに移動
array[ j + 1 ] = array[ j ] ;
array[ i ] = x ;
size++ ;
}
void add( int x ) {
int i ;
for( i = 0 ; i < size ; i++ ) {
if ( array[ i ] > x )
break ;
}
// for( int j = i ; j < size ; j++ )
// array[ j + 1 ] = array[ j ] ;
for( int j = size - 1 ; j >= i ; j-- )
array[ j + 1 ] = array[ j ] ;
array[ i ] = x ;
size++ ;
}
このプログラムでは、for( i … ) の処理でデータを挿入すべき場所を見つけ、for( int j … ) の繰り返しでデータを1つ後ろにずらしてから要素を加えている。
for( i … ) の処理は、このプログラムでは O( N ) となっているが、2分探索法を用いれば O( log N ) に改善ができるかもしれない。しかし、for( int j… ) の処理は、データを1つ後ろにずらす必要があるため O( N ) の処理が必要となる。
ここで、途中にデータを追加する処理の効率を改善することを考える。
リスト構造の導入
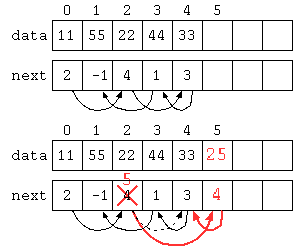
以下のデータ構造では、配列にデータと次のデータの場所を覚えることで、一見デタラメな順序に保存されているようにみえるが、next[] に次の値の保存されている場所が入っている。
import java.util.*;
public class Main { // 0 1 2 3 4 5
static int[] data = new int[] { 11 , 55 , 22 , 44 , 33 , 0 , 0 , 0 , 0 , 0 } ;
static int[] next = new int[] { 2 , -1 , 4 , 1 , 3 , 0 , 0 , 0 , 0 , 0 } ;
static int size = 5 ;
static int top = 0 ;
static void insert( int n , int x ) {
data[ size ] = x ;
next[ size ] = next[ n ] ;
next[ n ] = size ;
size++ ;
}
public static void main(String[] args) throws Exception {
for( int idx = top ; idx >= 0 ; idx = next[ idx ] )
System.out.println( data[ idx ] ) ;
insert( 2 , 25 ) ;
for( int idx = top ; idx >= 0 ; idx = next[ idx ] )
System.out.println( data[ idx ] ) ;
}
}
#include <stdio.h>
int data[ 10 ] = { 11 , 55 , 22 , 44 , 33 , 0 , 0 , 0 , 0 , 0 } ;
int next[ 10 ] = { 2 , -1 , 4 , 1 , 3 , 0 , 0 , 0 , 0 , 0 } ;
int size = 5 ;
int top = 0 ;
void insert( int n , int x ) {
data[ size ] = x ;
next[ size ] = next[ n ] ;
next[ n ] = size ;
size++ ;
}
int main() {
for( int idx = top ; idx >= 0 ; idx = next[ idx ] )
printf( "%d\n" , data[ idx ] ) ;
insert( 2 , 25 ) ;
for( int idx = top ; idx >= 0 ; idx = next[ idx ] )
printf( "%d\n" , data[ idx ] ) ;
return 0 ;
}
このようなデータ構造であれば、データ自体は末尾に保存しているが、次の値が入っている場所を修正することで途中にデータを挿入することができる。この方法であれば、途中にデータを入れる場合でもデータを後ろにずらすような処理が不要であり、O(1)で途中にデータを挿入できる。
同じプログラムを、データと次のデータの配列番号のオブジェクトで記述してみた。
import java.util.*;
class DataNext {
public int data ;
public int next ;
DataNext( int d , int n ) {
this.data = d ;
this.next = n ;
}
}
public class Main {
public static DataNext[] table = {
new DataNext( 11 , 2 ) ,
new DataNext( 55 , -1 ) ,
new DataNext( 22 , 4 ) ,
new DataNext( 44 , 1 ) ,
new DataNext( 33 , 3 ) ,
null ,
null ,
null ,
null ,
null ,
} ;
public static int size = 5 ;
public static void insert( int n , int x ) {
table[ size ] = new DataNext( x , table[ n ].next ) ;
table[ n ].next = size ;
size++ ;
}
public static void main(String[] args) throws Exception {
for( int idx = 0 ; idx >= 0 ; idx = table[ idx ].next )
System.out.println( table[ idx ].data ) ;
insert( 2 , 25 ) ;
for( int idx = 0 ; idx >= 0 ; idx = table[ idx ].next )
System.out.println( table[ idx ].data ) ;
}
}
- オブジェクトで途中に挿入(Paiza.io)
このプログラムでは、配列の当初の長さを超えてデータを格納することはできない。
リスト構造 ListNode
前述の data と next で次々とデータを続けて保存するために、リスト構造(連結リスト)を定義する。
import java.util.*;
class ListNode {
int data ;
ListNode next ;
ListNode( int d , ListNode nx ) {
this.data = d ;
this.next = nx ;
}
} ;
public class Main {
public static void main(String[] args) throws Exception {
ListNode top = new ListNode( 11 , new ListNode( 22 , new ListNode( 33 , null ) ) ) ;
for( ListNode p = top ; p != null ; p = p.next )
System.out.println( p.data ) ;
top.next = new ListNode( 15 , top.next ) ;
for( ListNode p = top ; p != null ; p = p.next )
System.out.println( p.data ) ;
}
}
#include <stdio.h>
#include <stdlib.h>
struct ListNode {
int data ;
ListNode* next ;
} ;
ListNode* newListNode( int d , ListNode* nx ) {
ListNode* _this = new ListNode() ;
if ( _this != NULL ) {
_this->data = d ;
_this->next = nx ;
}
return _this ;
}
int main() {
ListNode* top = newListNode( 11 , newListNode( 22 , newListNode( 33 , NULL ) ) ) ;
for( ListNode* p = top ; p != NULL ; p = p->next )
printf( "%d\n" , p->data ) ;
top->next = newListNode( 15 , top->next ) ;
for( ListNode* p = top ; p != NULL ; p = p->next )
printf( "%d\n" , p->data ) ;
return 0 ;
}
Javaのジェネリクス
Javaのジェネリクス(C++のテンプレート)を使って書いてみた。ジェネリクスは、クラスやメソッドにおいて、特定の型を指定することなく動作するコードを記述することができる機能。これにより、型安全性を保ちながら、コードの再利用性と柔軟性を向上させることがでる。
import java.util.*; class ListNode<T> { T data ; ListNode<T> next ; ListNode( T d , ListNode<T> n ) { this.data = d ; this.next = n ; } } ; public class Main { public static void main(String[] args) throws Exception { // var 宣言は型推論で、右辺のデータ型を自動的に選択してくれる。 // itop は整数型のリスト var itop = new ListNode<Integer>( 11 , new ListNode<Integer>( 22 , new ListNode<Integer>( 33 , null ) ) ) ; // new List<int>( 11 , ... ) と書くと、<>の中は reference しか使えないと言われる。 for( var p = itop ; p != null ; p = p.next ) System.out.println( p.data ) ; // stop は文字列型のリスト var stop = new ListNode<String>( "aa" , new ListNode<String>( "bb" , new ListNode<String>( "cc" , null ) ) ) ; for( var p = stop ; p != null ; p = p.next ) System.out.println( p.data ) ; } }前述のプログラムをJavaのジェネリッククラスで記述
import java.util.*; public class Main { public static void main(String[] args) throws Exception { // LinkedList は上記のリスト構造で保存される。 // 途中に要素の追加削除を行ったり、シーケンシャルアクセスに向いたデータ構造 var top = new LinkedList<Integer>() ; top.add( 11 ) ; top.add( 22 ) ; top.add( 33 ) ; for( int i : top ) // 11 22 33 System.out.println( i ) ; top.add( 1 , 15 ) ; for( int i : top ) // 11 15 22 33 System.out.println( i ) ; } }
クラスの宣言とコンストラクタ・メソッド
import java.util.*;
// クラス宣言
class Person {
// データ構造
String name ;
int age ;
// コンストラクタ(データ構造を初期化する関数)
Person( String n , int x ) {
this.name = n ; // this は対象となるデータそのものを指す
this.age = x ; // 対象が明言されていれば、this は省略可能
}
// データを扱うメソッド
void print() { // データを表示
System.out.println( this.name + "," + this.age ) ;
}
boolean sameAge( Person x ) { // 同じ年齢か判断するメソッド
return this.age == x.age ;
}
} ;
public class Main {
public static void main(String[] args) throws Exception {
Person tsaitoh = new Person( "Tohru Saitoh" , 59 ) ;
Person tomoko = new Person( "Tomoko Saitoh" , 48 ) ;
tsaitoh.print() ; // Tohru Saitoh, 59
tomoko.print() ; // Tomoko Saitoh,48
if ( tsaitoh.sameAge( tomoko ) ) {
// sameAge( Person x ) では、
// this = tsaitoh , x = tomoko となって呼び出される
System.out.println( "同じ年齢ですよ" ) ;
}
Person[] family = new Person[ 2 ] ;
family[0] = tsaitoh ;
family[1] = tomoko ;
for( int i = 0 ; i < 2 ; i++ )
family[ i ].print() ;
}
}こ
このプログラムのデータ構造は下記のような状態。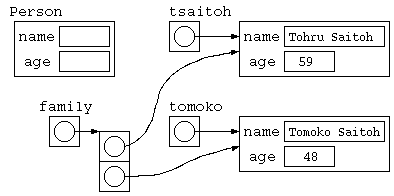
Javaのオブジェクト指向の基礎
前期中間前レポート課題(選択2)
4年の情報構造論で、リスト構造などの内容を進める前に、3年プログラミング応用でクラスなどに自信がない人向けの簡単レクチャ。
クラスは、データ構造と手続き
例えば、名前と年齢のデータをクラスで扱うのであれば、以下のようなコードが基本となるだろう。
import java.util.*;
class NameAge {
String name ; // インスタンス変数
int age ; // インスタンス変数
static int count = 0 ; // クラス変数
// コンストラクタ
NameAge( String s , int a ) {
this.name = s ;
this.age = a ;
count++ ;
}
// メソッド
void print() {
System.out.println( this.name + "," + this.age ) ;
System.out.println( "member = " + count ) ;
}
} ;
public class Main {
public static void main(String[] args) throws Exception {
NameAge tsaitoh = new NameAge( "tsaitoh" , 59 ) ;
tsaitoh.print() ;
System.out.println( "age = " + tsaitoh.age ) ;
NameAge tomoko = new NameAge( "tomoko" , 48 ) ;
tomoko.print() ;
}
}
実行結果
tsaitoh,59
member = 1
age = 59
tomoko,48
member = 2
- オブジェクト指向の基礎(Paiza.io)
クラスとは、データ構造(オブジェクト)とそのデータ構造を扱うための関数(メソッド)をまとめて扱う。
クラス NameAge の中で宣言されている、NameAge() の関数は、オブジェクトを初期化するための関数(メソッド)であり、特にコンストラクタと呼ばれる。
実際にデータを保存するための tsaitoh や tomoko とよばれる変数に NameAge オブジェクトの実体(インスタンス)を作る時には 「new クラス名」 とやることで、初期化ができる。
イメージでは、下図のようなデータ構造ができあがる。
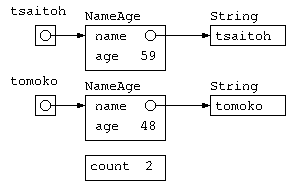
でも、年齢の覚え方は、将来的に誕生日を覚えるように変化するかもしれない。この際に、Main 関数の中で age を使うと後で混乱の元になるかもしれない。こういう時は、NameAge クラス以外では中身を勝手に使わせないために、インスタンス変数などに public / private といったアクセス制限を加える。
import java.util.*;
class NameAge {
private String name ; // インスタンス変数
private int age ; // インスタンス変数
public static int count = 0 ; // クラス変数
// コンストラクタ
public NameAge( String s , int a ) {
this.name = s ;
this.age = a ;
count++ ;
}
// メソッド
public void print() {
System.out.println( this.name + "," + this.age ) ;
System.out.println( "member = " + count ) ;
}
} ;
public class Main {
public static void main(String[] args) throws Exception {
NameAge tsaitoh = new NameAge( "tsaitoh" , 59 ) ;
tsaitoh.print() ;
System.out.println( "age = " + tsaitoh.age ) ;
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ここがエラーになる。NameAge::age は private
NameAge tomoko = new NameAge( "tomoko" , 48 ) ;
tomoko.print() ;
}
}
クラス自体も、public class NameAge … のように宣言することもあるが、public なクラスは 1つ の *.java ファイルの中に1つしか書けないというルールがあるので要注意。
練習問題
科目(Subject)と学生(Student)の情報があり、科目を受講した成績(Result)で成績を管理している。
このデータを管理するためのクラスを宣言し、下に示すようなデータSubject,Result,Studentの配列を作り、下に示したような出力が得られるプログラムを作成せよ。
科目: Subject
id name teacher // Subject[] subject_table = {
10010 情報構造論 t-saitoh // new Subject( 10010 , "情報構造論" , "t-saitoh" ) ,
10020 電気磁気学 takaku // new Subject( ....
10030 電気回路 komatsu // } ;
成績: Result
s_id id point // Result[] result_table = {
58563 10020 83 // new Result( 16213 , 10020 , 83 ) ,
58564 10010 95 // new Result( ...
58573 10030 64 // } ;
58563 10010 89
学生: Student
s_id name age // Student[] student_table = {
58563 斉藤太郎 18 // new Student( 16213 , "斉藤太郎" , 18 ) ,
58564 山田次郎 19 // new Student( ...
58573 渡辺花子 18 // } ;
以下のようなデータが出力されること
斉藤太郎 電気磁気学 83
渡辺花子 情報構造論 95
山田次郎 電気回路 64
斉藤太郎 情報構造論 89
- 課題のひな形(Paiza.io)
処理速度を計測
前期中間前レポート課題(選択1)
例年であれば、プログラム作成中心のレポート課題をやってもらっているけど、前期中間試験は今回早めに行われるので、プログラム作成か、処理速度のオーダを実際に計測実験のいずれかとする。
現在時間を ミリ秒の精度で求める System.currentTimeMills() を使って、様々なプログラムの処理時間を計測してみよう。ただし、OS によって 100ミリ秒未満はあまり正確に測れない。このため、処理時間は繰り返し処理などを入れることで、10秒程度になるようにすること。また、動作例で示した Paiza.io では、長い処理時間のプログラムは、途中で強制終了させられるので、自分のパソコンにインストールしてある環境で動作させること。また、並列処理しているプログラムの影響を受ける可能性もあることから、他の処理の影響がでないように工夫すること。
様々なプログラムの実行時間を計測してみよう
import java.util.*;
public class Main {
// 乱数を配列にセット
public static void array_set_random( int[] array ) {
Random rnd = new Random() ;
for( int i = 0 ; i < array.length ; i++ )
array[ i ] = rnd.nextInt( array.length ) ;
}
// 配列を選択法でソート
public static void array_sort( int[] array ) {
for( int i = 0 ; i < array.length - 1 ; i++ ) {
int min = i , j ;
for( j = i + 1 ; j < array.length ; j++ ) {
if ( array[ min ] > array[ j ] )
min = j ;
}
int tmp = array[ i ] ;
array[ i ] = array[ min ] ;
array[ min ] = tmp ;
}
}
public static void main(String[] args) throws Exception {
// 変化させるデータ件数
int[] data_n = {
2500 ,
5000 ,
7500 ,
10000
} ;
for( int i = 0 ; i < data_n.length ; i++ ) {
int[] array = new int[ data_n[ i ] ] ;
// 配列を乱数で埋める時間は測りたくない
array_set_random( array ) ;
long start = System.currentTimeMillis() ;
array_sort( array ) ;
// ソート結果の表示時間は測りたくない
//for( int x = 0 ; x < array.length ; x++ )
// System.out.print( array[ x ] + " " ) ;
//System.out.println() ;
long end = System.currentTimeMillis() ;
System.out.println( "Time = " + (end - start) ) ;
}
}
}
- データ件数と処理時間の計測(Paiza.io)

プログラムによっては、処理時間が短すぎる場合があるので、下記のように 1000 回ループさせるなどで、一定時間以上の処理となるように工夫すること。
public static int fact( int x ) {
if ( x == 1 )
return 1 ;
else
return x * fact( x - 1 ) ;
}
public static void main(String[] args) throws Exception {
int[] data_n = { 2 , 4 , 6 , 8 , 10 } ;
for( int i = 0 ; i < data_n.length ; i++ ) {
long start = System.currentTimeMillis() ;
for( int j = 0 ; j < 1000 ; j++ ) {
int ans = fact( data_n[ i ] ) ;
}
long end = System.currentTimeMillis() ;
System.out.println( "Time = " + ( end - start ) ) ;
}
}
レポート内容
データ件数や 引数に与える数によって、処理時間が変化するプログラムを記述し、そのプログラムを N を変化させながら上記のプログラムなどを参考に処理時間を計測する。時間計測には誤差が大きく含まれる可能性があることから、複数回実行して平均をとるなどの工夫もすること。
授業中に示したプログラムなどの計測を行う場合は、ループのプログラムの変化と、別プログラムの再帰の場合の変化の2つについて結果を示すこと。創造工学演習の再帰問題の課題の整数比の直角三角形探索、辺の組み合わせ問題、N Queen、ハノイの塔など、自分で興味のあるテーマを選んだ場合は1つでも良い。
この上で、(1) プログラムリスト, (2) 時間計測にあたり工夫したこと, (3) 実際の実行結果のグラフ, (4) その結果の考察した結果をレポートにまとめて提出せよ。
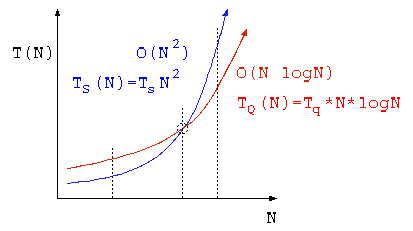
クイックソートと選択ソート
データ数 N = 10 件でソート処理の時間を計測したら、選択ソートで 10msec 、クイックソートで 20msec であった。
- データ件数 N= 100 件では、選択法,クイックソートは、それぞれどの程度の時間がかかるか答えよ。
- TS(10)=Ts x 100 = 10msec よって Ts = 0.1msec
- 0.1msec * 100 * 100 = 1000 msec
- TQ(10)=Tq x 10 x log10 10 = 20msec よって Tq=2msec
- 2msec * 100 * log10 100 = 400 msec
- TS(10)=Ts x 100 = 10msec よって Ts = 0.1msec
- データ件数何件以上なら、クイックソートの方が高速になるか答えよ。
-
- 2025-05-01-qsort-sel.xlsx より 30件以上
設問2 は、通常の関数電卓では求まらないので、数値的に方程式を解く機能を持った電卓が必要。
上記の計算時間は、計算しやすい値を例に示したが、一般的なプロセッサであれば、10件~30件程度で選択ソートとクイックソートの処理時間が入れ替わる。
これらを踏まえ、ライブラリとして使われるクイックソートプログラムでは、データ件数が20件ほど未満になったら、ソート方法を選択ソートに切り替えるように作られている。
ハノイの塔と再帰を使った並び替え
ハノイの塔
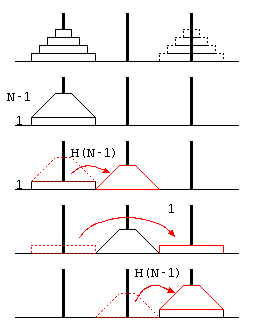 ここまでは、簡単な再帰呼び出しのプログラムを例にして再帰方程式などの説明を行った。次に「ハノイの塔」の処理時間を例題に、プログラムの処理時間について分析を行う。
ここまでは、簡単な再帰呼び出しのプログラムを例にして再帰方程式などの説明を行った。次に「ハノイの塔」の処理時間を例題に、プログラムの処理時間について分析を行う。
ハノイの塔は、3本の塔にN枚のディスクを積み、(1)1回の移動ではディスクを1枚しか動かせない、(2)ディスクの上により大きいディスクを積まない…という条件で、山積みのディスクを目的の山に移動させるパズル。
一般解の予想
ハノイの塔の移動回数を とした場合、 少ない枚数での回数の考察から、 以下の一般式で表せることが予想できる。
… ①
この予想が常に正しいことを証明するために、ハノイの塔の処理を、 最も下のディスク1枚への操作と、その上の(N-1)枚のディスクへの操作に分けて考える。
再帰方程式
上記右の図より、N枚の移動をするためには、上に重なるN-1枚を移動させる必要があるので、
… ②
… ③
ということが言える。(これがハノイの塔の移動回数の再帰方程式)
ディスクが枚の時、予想①が正しいのは明らか①,②。
ディスクが 枚で、予想が正しいと仮定すると、
枚では、
… ③より
… ①を代入
… ①の
の場合
となり、 枚でも、予想が正しいことが証明された。 よって数学的帰納法により、1枚以上で予想が常に成り立つことが証明できた。
これらのことから、ハノイの塔の処理時間は、で表せる。
再帰を用いた並び替え
データを並び替えるプログラムとして、繰り返し処理の分析では「選択法」について説明した。
選択法は、 のアルゴリズムで、あまり速い並び替え手法ではない。
| アルゴリズム | 処理時間のオーダー | ||
|---|---|---|---|
| バブルソート | |||
| 選択ソート | |||
| クイックソート, マージソート |
ここで、最も高速なアルゴリズムとしては、クイックソートが有名である。クイックソートプログラムは、処理時間のオーダはで表せる。
本当であれば、クイックソートのプログラムの処理時間の分析を説明したいけど、イメージがわかりにくいので、同じオーダ式であらわせるマージソートで説明を行う。
(マージソートのオーダは、クイックソートと同じだけど、計算途中のデータを一時的に覚える場所を確保する処理が必要で、その処理に手間がかかるため、効率はクイックソートに比べ遅くなる。)
import java.util.*;
// マージソートは、リスト構造を使っているので、
// クイックソートより効率が悪い。
// でもオーダーとしては、O( N log N ) のアルゴリズム
public class Main {
public static LinkedList merge_sort( LinkedList list ) {
// データ件数が1件ならソート不要
if ( list.size() <= 1 ) {
return list;
}
// 左右2つに分割
int mid = list.size() / 2 ;
LinkedList<Integer> left = new LinkedList<>( list.subList( 0 , mid ) ) ;
LinkedList<Integer> right = new LinkedList<>( list.subList( mid , list.size() ) ) ;
// 左右をそれぞれマージソート
LinkedList<Integer> sorted_left = merge_sort( left ) ;
LinkedList<Integer> sorted_right = merge_sort( right ) ;
// 左右のリストをマージする。
LinkedList merged = new LinkedList<>() ; // 初期状態は空っぽ
// 左右のリストの小さい方を取り出して答えに追加していく
while( !sorted_left.isEmpty() && !sorted_right.isEmpty() ) {
int left_top = sorted_left.get( 0 ) ;
int right_top = sorted_right.get( 0 ) ;
if ( left_top > right_top ) {
merged.add( sorted_right.removeFirst() ) ;
} else {
merged.add( sorted_left.removeFirst() ) ;
}
}
// 残ったリストを追加
while( !sorted_left.isEmpty() )
merged.add( sorted_left.removeFirst() ) ;
while( !sorted_right.isEmpty() )
merged.add( sorted_right.removeFirst() ) ;
return merged ;
}
public static void main( String[] args ) {
// ソート対象のデータ
LinkedList<Integer> data = new LinkedList<>() ;
data.add( 38 ) ;
data.add( 27 ) ;
data.add( 43 ) ;
data.add( 3 ) ;
data.add( 9 ) ;
data.add( 82 ) ;
data.add( 10 ) ;
System.out.println( "ソート前: " + data ) ;
LinkedList<Integer> sorted_data = merge_sort( data ) ;
System.out.println( "ソート後: " + sorted_data ) ;
}
}
- LinkedListを用いたマージソート(Paiza.io)
マージソートの分析
マージソートは、与えられたデータを2分割し、 その2つの山をそれぞれマージソートを行う。 この結果の2つの山の頂上から、大きい方を取り出す…という処理を繰り返すことで、 ソートを行う。
このことから、再帰方程式は、以下のようになる。
この再帰方程式を、N=1,2,4,8…と代入を繰り返していくと、 最終的に処理時間のオーダが、 となる。
:
よって、
選択法とクイックソートの処理時間の比較
データ数 N = 10 件でソート処理の時間を計測したら、選択法で 10msec 、クイックソートで 20msec であった。
- データ件数 N= 100 件では、選択法,クイックソートは、それぞれどの程度の時間がかかるか答えよ。
- データ件数何件以上なら、クイックソートの方が高速になるか答えよ。
設問2 は、通常の関数電卓では求まらないので、数値的に方程式を解く機能を持った電卓が必要。
再帰呼び出しと処理時間の見積もり
再帰呼び出しの基本
次に、再帰呼び出しを含むような処理の処理時間見積もりについて解説をおこなう。そのまえに、再帰呼出しと簡単な処理の例を説明する。
再帰関数は、自分自身の処理の中に「問題を小さくした」自分自身の呼び出しを含む関数。プログラムには問題が最小となった時の処理があることで、再帰の繰り返しが止まる。
// 階乗 (末尾再帰)
int fact( int x ) {
if ( x <= 1 )
return 1 ;
else
return x * fact( x-1 ) ;
}
// ピラミッド体積 (末尾再帰)
int pyra( int x ) {
if ( x <= 1 )
return 1 ;
else
return x*x + pyra( x-1 ) ;
}
// フィボナッチ数列 (非末尾再帰)
int fib( int x ) {
if ( x <= 2 )
return 1 ;
else
return fib( x-1 ) + fib( x-2 ) ;
}
import java.util.*;
public class Main {
// 階乗(末尾再帰)
public static int fact( int x ) {
if ( x <= 1 )
return 1 ;
else
return x * fact( x - 1 ) ;
}
// ピラミッド体積(末尾再帰)
public static int pyra( int x ) {
if ( x <= 1 )
return 1 ;
else
return x * x + pyra( x - 1 ) ;
}
// フィボナッチ数列 (非末尾再帰)
public static int fib( int x ) {
if ( x <= 2 )
return 1 ;
else
return fib( x - 1 ) + fib( x - 2 ) ;
}
public static void main(String[] args) throws Exception {
System.out.println( "fib(5)=" + fib( 5 ) ) ;
System.out.println( "pyra(5)=" + pyra( 5 ) ) ;
System.out.println( "fib(5)=" + fib( 5 ) ) ;
}
}
- 単純な再帰関数(Paiza.io)
階乗 fact(N) を求める処理は、以下の様に再帰が進む。

また、フィボナッチ数列 fib(N) を求める処理は以下の様に再帰が進む。

再帰呼び出しの処理時間
次に、この再帰処理の処理時間を説明する。 最初のfact(),pyra()については、 x=1の時は、関数呼び出し,x<=1,return といった一定の処理時間を要し、T(1)=Ta で表せる。 x>1の時は、関数呼び出し,x<=1,*,x-1,returnの処理(Tb)に加え、x-1の値で再帰を実行する処理時間T(N-1)がかかる。 このことから、 T(N)=Tb=T(N-1)で表せる。
} 再帰方程式
このような、式の定義自体を再帰を使って表した式は再帰方程式と呼ばれる。これを以下のような代入の繰り返しによって解けば、一般式 が得られる。
T(1)=Ta
T(2)=Tb+T(1)=Tb+Ta
T(3)=Tb+T(2)=2×Tb+Ta
:
T(N)=Tb+T(N-1)=Tb + (N-2)×Tb+Ta
一般的に、再帰呼び出しプログラムは(考え方に慣れれば)分かりやすくプログラムが書けるが、プログラムを実行する時には、局所変数や関数の戻り先を覚える必要があり、深い再帰ではメモリ使用量が多くなる。
ただし、fact() や pyra() のような関数は、プログラムの末端で再帰が行われている。(fib()は、再帰の一方が末尾ではない)
このような再帰は、末尾再帰(tail recursion) と呼ばれ、関数呼び出しの return を、再帰処理の先頭への goto 文に書き換えるといった最適化が可能である。言い換えるならば、末尾再帰の処理は繰り返し処理に書き換えが可能である。このため、末尾再帰の処理をループにすれば再帰のメモリ使用量の問題を克服できる。
ここで、フィボナッチ数列のプログラムは、末尾再帰ではない。この fib( intx ) の処理時間を表す再帰方程式は、どのような式で表せるだろうか?
再帰を含む一般的なプログラム例
ここまでのfact()やpyra()のような処理の再帰方程式は、再帰の度にNの値が1減るものばかりであった。もう少し一般的な再帰呼び出しのプログラムを、再帰方程式で表現し、処理時間を分析してみよう。
以下のプログラムを実行したらどんな値になるであろうか?それを踏まえ、処理時間はどのように表現できるであろうか?
int array[ 8 ] = {
3 , 6 , 9 , 1 , 8 , 2 , 4 , 5 ,
} ;
int sum( int a[] , int L , int R ) { // 非末尾再帰
if ( R - L == 1 ) {
return a[ L ] ;
} else {
int M = (L + R) / 2 ;
return sum( a , L , M ) + sum( a , M , R ) ;
}
}
int main() {
printf( "%d¥n" , sum( array , 0 , 8 ) ) ;
return 0 ;
}
import java.util.*;
public class Main {
public static int[] array = {
3 , 6 , 9 , 1 , 8 , 2 , 4 , 5 ,
} ;
public static int sum( int[] a , int L , int R ) {
if ( R - L == 1 ) {
return a[ L ] ;
} else {
int M = (L + R) / 2 ;
return sum( a , L , M ) + sum( a , M , R ) ;
}
}
public static void main(String[] args) throws Exception {
System.out.println( "sum()=" + sum( array , 0 , array.length ) ) ;
}
}
- 再帰による配列の合計(分割統治法?)(Paiza.io)
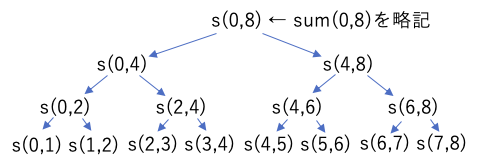
このプログラムでは、配列の合計を計算しているが、引数の L,R は、合計範囲の 左端(左端のデータのある場所)・右端(右端のデータのある場所+1)を表している。そして、再帰のたびに2つに分割して解いている。
このような、処理を(この例では半分に)分割し、分割したそれぞれを再帰で計算し、その処理結果を組み合わせて最終的な結果を求めるような処理方法を、分割統治法と呼ぶ。
このプログラムでは、対象となるデータ件数(R-L)をNとおいた場合、実行される命令からsum()の処理時間Ts(N)は次の再帰方程式で表せる。
← Tβ + (L〜M)の処理時間 + (M〜R)の処理時間
これを代入の繰り返しで解いていくと、
ということで、このプログラムの処理時間は、 で表せる。
ハノイの塔
 ここまでは、簡単な再帰呼び出しのプログラムを例にして再帰方程式などの説明を行った。次に「ハノイの塔」の処理時間を例題に、プログラムの処理時間について分析を行う。
ここまでは、簡単な再帰呼び出しのプログラムを例にして再帰方程式などの説明を行った。次に「ハノイの塔」の処理時間を例題に、プログラムの処理時間について分析を行う。
ハノイの塔は、3本の塔にN枚のディスクを積み、(1)1回の移動ではディスクを1枚しか動かせない、(2)ディスクの上により大きいディスクを積まない…という条件で、山積みのディスクを目的の山に移動させるパズル。
一般解の予想
ハノイの塔の移動回数を とした場合、 少ない枚数での回数の考察から、 以下の一般式で表せることが予想できる。
… ①
この予想が常に正しいことを証明するために、ハノイの塔の処理を、 最も下のディスク1枚への操作と、その上の(N-1)枚のディスクへの操作に分けて考える。
再帰方程式
上記右の図より、N枚の移動をするためには、上に重なるN-1枚を移動させる必要があるので、
… ②
… ③
ということが言える。(これがハノイの塔の移動回数の再帰方程式)
ディスクが枚の時、予想①が正しいのは明らか①,②。
ディスクが 枚で、予想が正しいと仮定すると、
枚では、
… ③より
… ①を代入
… ①の
の場合
となり、 枚でも、予想が正しいことが証明された。 よって数学的帰納法により、1枚以上で予想が常に成り立つことが証明できた。
これらのことから、ハノイの塔の処理時間は、で表せる。