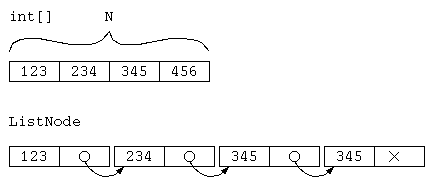
プログラムのバージョン管理とオープンソース
プログラムを複数人で開発する場合のバージョン管理と、オープンソースプログラムを使う場合の注意を説明する。
バージョン管理システム
プログラムを学校や自宅のパソコンで開発する場合、そのソースコードはどのように持ち運び管理修正すべきだろうか? また、そのソースコードを複数人で開発する場合は、どのように管理修正すべきだろうか?
最も原始的な方法は、常に全部を持ち歩く方法かもしれない。しかし、プログラムが巨大になってくるとコピーに時間がかかる。またコピーを取る時に、どれが最新なのか正しく把握する必要がある。
- 同期方式 – 2つのディレクトリのファイルの古い日付のファイルを、新しい日付のファイルで上書きするようなディレクトリ同期ソフトを使って管理
- 圧縮保管 – ファイル全体だと容量も多いため、複数のファイルを1つのファイルにまとめて圧縮を行う tar コマンドを使うことも多い。(tar ball管理)
diffとpatch
プログラムの修正を記録し、必要最小限で修正箇所の情報を共有する方式に patch がある。これには、2つのファイルの差異を表示する diff コマンドの出力結果(通称patch)を用る。diff コマンドでは、変更のある場所の前後数行の差異を !(入替) +(追加) -(削除) の目印をつけて出力する。patch コマンドに diff の出力を与えると、!,+,- の情報を元に修正を加えることができる。(通称「patchをあてる」)
((( helloworld-old.c )))
#include <stdio.h>
void main() {
printf( "Hello World\n" ) ;
}
((( helloworld.c )))
#include <stdio.h>
int main( void ) {
printf( "Hello World\n" ) ;
return 0 ;
}
((( diff の実行 )))
$ diff -c helloworld-old.c helloworld.c
((( 生成された patch 情報 )))
*** helloworld-old.c 2022-07-25 10:09:10.694442400 +0900
--- helloworld.c 2022-07-25 10:09:26.136433100 +0900
***************
*** 1,5 ****
#include <stdio.h>
! void main() {
printf( "Hello World\n" ) ;
}
--- 1,6 ----
#include <stdio.h>
! int main( void ) {
printf( "Hello World\n" ) ;
+ return 0 ;
}
インターネットの初期の頃には、他の人のプログラムに対して間違いを見つけると、作者に対してこのpatch(diff出力)をメールなどで送付し、patchコマンドでプログラムの修正が行われた。
広く世界で使われている Web サーバ apache は、オープンソースで開発されてきた。当初はプログラム公開後に間違いや機能追加の情報(patch)が世界中のボランティア開発者から送られてきながら改良が加えられていった。このため、”a too many patches”「つぎはぎだらけ」という自虐的皮肉を込めて apache と名付けられたと言われている。
初期のバージョン管理システム
バージョン管理システムは、複数人で少しづつテキストファイルに修正を加えながら改良を行うような際に、誰がどのような修正を行ったかという修正履歴を管理するためのツール。unix などのプログラム管理では rcs (revision control system) が使われていたが、その改良版として cvs (concurrent version system) が使われるようになっていった。(現在は後に紹介する Git などが主流)
- ci コマンド(check in) – ファイルをバージョン管理の対象として登録する。
- co コマンド(check out) – ファイルを編集対象とする(必要に応じて書き込みロックなども可能)。co されたファイルは、編集した人が ci して戻すまで ci することができない。
- 修正結果を ci する際には、新しい編集のバージョン番号などをつけて保存される。
- co コマンドでは、バージョン番号を指定してファイルを取り出すことも可能。
[Bさんの修正] /check out \check in ファイルver1.0-----→ver1.1------→ver1.2 \check out /check in [Aさんの修正]
集中管理型バージョン管理システム
rcs,cvs では、ファイルのバージョンは各ファイルを対象としているため、ファイルやディレクトリの移動や削除は管理が困難であった。これらの問題を解決するために、集中管理を行うサーバを基点として、対象ファイルのディレクトリ全体(ソースツリー)に対してバージョン番号を振って管理を行う。subversion はサーバに ssh などのネットワークコマンドを介して、保存・改変を行うことができる。
しかし、複数の人の修正のマージ作業の処理効率が悪く、処理速度が遅いため使われなくなっていった。同様のバージョン管理システムが企業により有償開発されていた(BitKeeperなど)が製品のライセンス問題が発生し、業を煮やした Linux 開発の Linus が Git のベースを開発・公開している。
分散型バージョン管理システム
Gitは、プログラムのソースコードなどの変更履歴を記録・追跡するための分散型バージョン管理システムである。Linus によって開発され、ほかの多くのプロジェクトで採用されている。(以下wikipedia記事を抜粋加筆)
Gitは分散型のソースコード管理システムであるため、リモートサーバ等にある中心リポジトリの完全なコピーを手元(ローカル環境)に作成して、そのローカルリポジトリを使って作業を行う。
一般的な開発スタイルでは、大雑把に言えば、以下のようなステップの繰り返しで作業が行なわれる:
- git clone – リモートサーバ等にある中心リポジトリをローカルに複製する。
- git commit – ローカルでコンテンツの修正・追加・削除を行い、ローカルリポジトリに変更履歴を記録する。
- 必要に応じて過去の状態の閲覧や復元などを行う。場合によってはこのステップを何度か繰り返す。
- git push – ローカルの変更内容を中心リポジトリに反映させる。
- git merge – git push の段階で、作業者ごとの変更内容が衝突することもある。Gitが自動で解決できる場合もあれば、手動での解決する。
- git pull – 更新された中心リポジトリ(他者の作業内容も統合されている)をローカルの複製にも反映する。これによりローカル環境のコードも最新の内容になるので、改めてステップ2の作業を行う。
ローカルリポジトリ(Aさん) ver1.0a1 ver1.0a2 ver1.1a1 修正--(git commit)--修正--(git commit) 修正--(git commit) /git clone \git push /git pull Bさんの修正 中心リポジトリver1.0-----------------ver1.1 も含まれる \git clone /git push 修正--(git commit)--修正--(git commit) 編集の衝突が発生すると ver1.0b1 ver1.0b2 git merge が必要かも ローカルリポジトリ(Bさん)
GitHub
Git での中心リポジトリを保存・管理(ホスティング)するためのソフトウェア開発のプラットフォーム。コードの管理には Git を利用し GitHub 社によって保守されている。2018年よりマイクロソフトの傘下企業となっている。
GitHub では単なるホスティングだけでなく、プルリクエストやWiki機能(ドキュメントの編集・閲覧機能)といった、開発をスムーズに行うための機能も豊富である。(個人的な例:github.com/tohrusaitoh/)
GitHub で管理されているリポジトリには、公開リポジトリと非公開リポジトリがあり、非公開リポジトリはその管理者からの招待をうけないとリポジトリ改変に参加できない。
企業でのプログラム開発で GitHub を内々で使っている事例なども多いが、間違って公開リポジトリと設定されていて企業の開発中のプログラムが漏洩してしまった…との事例もあるので、企業での利用では注意が必要。
オープンソースとライセンス
オープンソースプログラムは、プログラムのソースコードをインターネットで公開されたものである。しかし、元となったプログラムの開発者がその利用に対していくつかの制約を決めていることが多い。これらのオープンソースプログラムでのソフトウェア開発手法の概念として「伽藍とバザール」を紹介する。
伽藍とバザール
伽藍(がらん)とは、優美で壮大な寺院のことであり、その設計・開発は、優れた設計・優れた技術者により作られた完璧な実装を意味している。バザールは有象無象の人の集まりの中で作られていくものを意味している。
たとえば、伽藍方式の代表格である Microsoft の製品は、優秀なプロダクトだが、中身の設計情報などを普通の人は見ることはできない。このため潜在的なバグが見つかりにくいと言われている。
これに対しバザール方式では明確な方針が決められないまま、インターネットで公開されているプログラムをボランティアを中心とした開発者を中心に開発していく手法である。
代表格の Linux は、インターネット上にソースコードが公開され、誰もがソースコードに触れプログラムを改良してもいい(オープンソース)。その中で、新しい便利な機能を追加しインターネットに公開されれば、良いコードは生き残り、悪いコードは自然淘汰されていく。このオープンソースを支えているツールとしては、前に述べた git が有名。
オープンソース・ライセンス
ソースコードを公開している開発者の多くは、ソフトウェア開発が公開することで発展することを期待する一方で、乱用をふせぐために何らかの制約をつけていることが多い。最初の頃は、開発者に敬意を示す意味で、プログラムのソースコードに開発者の名前を残すこと、プログラムを起動した時に開発者の名前が参照できること…といった条件の場合もあったが、最近ではソフトウェアが広く普及・発展することを願って条件をつけることも多い。
こういったオープンライセンスの元となったのは、Emacs(エディタ),gcc(コンパイラ)の開発者のストールマンであり、「ユーザーが自由にソフトウェアを実行し、(コピーや配布により)共有し、研究し、そして修正するための権利に基づいたソフトウェアを開発し提供することにより、ユーザーにそのような自由な権利を与えた上でコンピュータやコンピューティングデバイスの制御をユーザーに与えること」を目標に掲げた GNU プロジェクトがある。linux を触る際のコマンドで、g で始まるプログラムの多くは GNU プロジェクトのソフトウェア。
GNU プロジェクトが掲げる GNU ライセンス(GPL)では、GPLが適用されていれば、改良したソフトウェアはインターネットに公開する義務を引き継ぐ。オープンソースライセンスとして公開の義務の範囲の違いにより、BSD ライセンス、Apacheライセンスなどがある。
| コピーレフト型 | GNU ライセンス(GPL) | 改変したソースコードは公開義務, 組み合わせて利用では対応箇所の開示が必要。 |
| 準コピーレフト型 | LGPL, Mozilla Public License | 改変したソースコードは公開義務。 |
| 非コピーレフト型 | BSDライセンス Apacheライセンス |
ソースコードを改変しても公開しなくてもいい。 |
GPLライセンス違反
GPLライセンスのソフトウェアを組み込んで製品を開発した場合に、ソースコード開示を行わないとGPL違反となる。大企業でこういったGPL違反が発生すると、大きな風評被害による損害をもたらす場合がある。
- SwitchBot 社製品のGPL違反の注意喚起 – といっても2年間放置されてたの?
- SwitchBot 社が、この2023年7月に、GPL違反の注意喚起を受け、ようやく対応したようだ
最近のライセンスが関連する話題を1つ紹介:GitHub を使った AI プログラミング機能「Copilot」というサービスが提供されている。Copilot のプラグインをインストールした vscode(エディタ) では、編集している関数名や変数名などの情報と GitHub で公開されているプログラムの 学習結果を使って、関数名を数文字タイプするだけで関数名・引数・処理内容などの候補を表示してくれる。しかし、Copilot を使うと非オープンライセンスで開発していたプログラムに、オープンソースのプログラムが紛れ込む可能性があり、非オープンソースプロジェクトが GPL で訴えられる可能性を心配し「Copilot は使うべきでない」という意見の開発者も出ている。Copilot だけでなく、生成系 AI によるプログラムでも、同様の問題が指摘されている。
理解度確認
D/A・A/D変換回路と誤差
小型コンピュータを使った制御では、外部回路に指定した電圧を出力(D/A変換)したり、外部の電圧を入力(A/D変換)したりすることが多い。以下にその為の回路と動作について説明する。
D/A変換回路
ラダー抵抗回路によるD/A変換の仕組みを引用
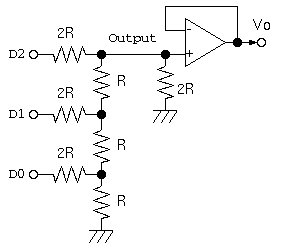
このような回路で、D0,D1,D2 は、デジタル値の0=0[V] , 1=5[V] であった場合、Output 部分の電圧は、(D0,D1,D2)の値が、(0,0,0),(0,0,1),…(1,1,1)と変化するにつれ、5/8[V]づつ増え、(1,1,1)で 5*(7/8)=4.4[V]に近づいていく。最後に、Output が出力によって電圧が変化しないように、アンプ回路を通す。
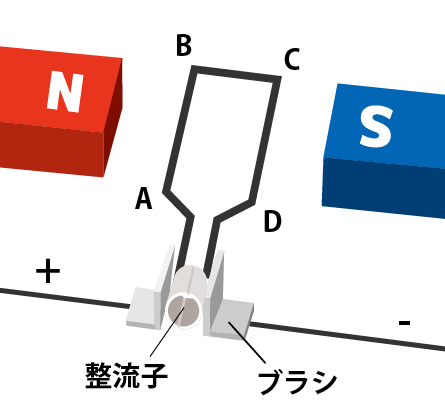
DCモータをアナログ量で制御しないこと
このように、電圧をコンピュータから制御するようになると、ロボットで模型用の直流モータの回転速度をこれで制御したい…と考えるかもしれない。
しかし、直流モータは、ブラシとコイル(電磁石)を組み合わせたものだが、モーターが回転しだす瞬間でみれば、コイルは単なる導線である。このため、小さい電流でゆっくりモータを回転させようとすると、たとえ小さい電圧でも導線(抵抗はほぼ0[Ω])には大量の電流が流れ、モータをスイッチングする回路は焼き切れるかもしれない。
PWM変調
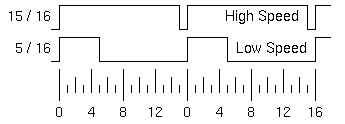
こういう場合には、PWM変調(Pulse Width Modulation) を行う。電圧の高さは一定で、高速回転させるときは長時間電圧をONにするが、低速回転させるときはONとOFFを繰り返し信号でONの時間を短くする。
このような波形であれば、低速度でも電流が流れる時間が短く、大量の電流消費は避けられ、モーターをまわす力も安定する。
A/D変換回路
D/A変換とは逆に、アナログ量をデジタル値に変換するには、どのようにするか?
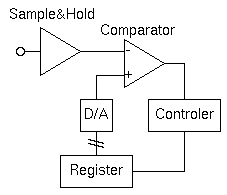
このような場合には、A/D変換回路を用いる。一般的な回路では、以下のような逐次比較型A/D変換を用いる。
この回路では、変換開始と共に入力値をサンプル保持回路でアナログ量を保存する。
その後、Registerの中のデジタル値を、D/A 変換回路でアナログ量に変換した結果を、比較器(Comparator)でどちらが大きいか判断し、その結果に応じて2分探索法とかハイアンドローの方式のように、比較を繰り返しながらデジタル値を入力値に近づけていく。
ハイアンドロー(数あてゲーム)
数あてゲームで、デタラメな0〜127までの整数を決めて、ヒントを元にその数字を当てる。回答者は、数字を伝えると、決めた数よりHighかLowのヒントをもらえる。
最も速い回答方法は…例えば決めた数が55だとすると
・初期状態 2進数 0..127 ・64 - Low 0?????? 0..63 ・32 - High 01????? 32..63 ・48 - High 011???? 48..63 ・56 - Low 0110??? 48..55 ・52 - High 01101?? 52..55 ・54 - High 011011? 54..55 ・55 - Bingo 0110111 55確定どんな値でも、7回(27=127)までで当てることができる。
逐次比較型A/D変換回路は、High&Lowゲームように値を求めることから、桁数に応じた変換時間を要する。
量子化と量子化誤差
アナログデータ(連続量)をデジタルデータなどの離散的な値で近似的に表すことを、量子化という。
量子化誤差とは、信号をアナログからデジタルに変換する際に生じる誤差のことをいう。
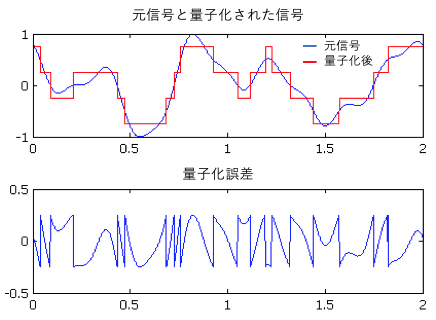
アナログ信号からデジタル信号への変換を行う際、誤差は避けられない。アナログ信号は連続的で無限の正確さを伴うが、デジタル信号の正確さは量子化の解像度やアナログ-デジタル変換回路のビット数に依存する。
偶然誤差
アナログ信号がA/D変換回路に入るまでに、アナログ部品の電気的変動(ノイズ)が原因で値が変動することもある。ノイズが時間的に不規則に発生し、値が増えてしまったり減ってしまったり偶然に発生するものは偶然誤差という。偶然誤差を加えると相殺されてほぼ0になるのであれば、統計的な手法で誤差の影響を減らすことができる。
系統誤差
ある特定の原因によって測定値が偏る誤差は、系統誤差と呼ぶ。例として、測定機器が持つ精度である器差によるもの、温度や湿度、気圧などが影響して発生するもの、測定方法の癖で値が偏るものなどがある。系統誤差は、誤差の要因が解ればその偏ったズレの量を調べて、測定した値からズレを引き算すれば補正することができる。
なぜデジタル信号を使うのか
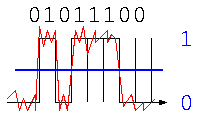
コンピュータが信号処理でなぜ使われるのか?例えば、下の信号のように、電圧の低い/高いで0/1を表現したとする。
ノイズが混入しづらい
このデータ”01011100″を通信相手に送る場合、通信の途中でノイズ(図中の赤)のような信号が加わった場合、アナログ信号では、どれがノイズなのか判別することはできない。しかしデジタル信号であれば、真ん中青線より上/下か?で判別すれば、小さいノイズの影響は無視して、元どおりの”01011100″を取り出せる。この0か1かを判別するための区切り(図中青線)は、しきい値と呼ばれる。
ノイズを見つける・治す
また、”01011100″のデータを送る通信の途中で、しきい値を越えるような大きなノイズが混ざって、受信したとする。この場合、単純に受け取るだけであれば、”01010100″で間違った値を受け取っても判別できない。しかし、データを送る際にパリティビット(偶数パリティであれば全データの1の数が偶数になるように)1ビットのデータを加える。このデータを受け取った際に、ノイズで1ビット反転した場合、1の数が奇数(3個)なので、ノイズでビット反転が発生したことがわかる。これをパリティチェックと言う。
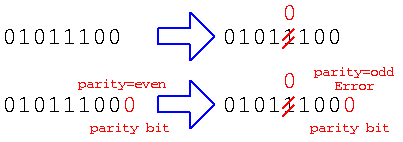
このように、デジタル信号を使えば、しきい値を越えない程度のノイズならノイズの影響を無視できるし、たとえ大きなノイズでデータに間違いがあっても、パリティチェックのような方法を使えば間違って伝わったことを判別できる。
パリティチェックは、元のデータに1bitの信号を追加することで誤り検出ができるが、2bit同時に変化してしまうと誤りを見つけられない。そこで、元データにさらに多くのbit情報を追加すると、1bitの間違いを元に戻すようにもできる。誤り検出・訂正
電子回路で制御するかコンピュータで制御するか
これ以外にも、デジタル信号にする理由がある。
アナログ回路(電子回路)で制御しようとすると、抵抗やコイルやコンデンサといった受動素子が必要となるが、その中でもコイルは小型化がしづらい部品で、制御回路全体の小型化が難しい。大量生産ができるような回路なら小型化ができるかもしれないが、多品種少量の生産物では小型化のための開発費用の元がとれない。しかし、大量生産された安価な小型コンピュータで制御すれば、制御回路全体の小型化も可能となる。
また、電子回路の特性を調整するには、抵抗などの部品をはんだ付けをしながら部品を交換することになるかもしれない。しかしながら、アナログ信号をデジタル信号にしてしまえば、ノイズを減らすための平均化処理などは計算で実現できるし、特性を変化させるための調整もプログラムの数値を変更するだけで可能となる。
Hook(フック)とは
卒研で汎用的な物を作っていく中で、本来の処理とは別に、この対象の時は、特別な処理をしたいということが出てくる。しかし、この処理を if ( … ) で管理するとプログラムのコードが煩雑となることも多い。この時のターゲットに応じた特別な処理は、Hook(フック)と呼ぶ。
「Hook(フック)」は、プログラミングにおいて、既存のプログラムの特定の処理の途中に、別のカスタムな処理を差し込む(「引っ掛ける」)ための仕組みを指します。まるでプログラムの実行の流れに「釣り針」を引っ掛けて、自分のコードを実行するようなイメージです。(Geminiより)
struct Target{
int id ; // 識別用のID
:
} ;
void action_Target( Target* t ) {
if ( t.id == T_FOO ) {
// 特別前処理_FOO
} else if ( t.id == T_BAR ) {
// 特別前処理_BAR
}
// 通常処理
:
if ( t.id == T_FOO ) {
// 特別後処理_FOO
} else if ( t.id == T_BAR ) {
// 特別後処理_BAR
}
}
このようなプログラムでは、action_Target() が、どんどん肥大化して、メンテナンスが面倒になる。
C言語であれば、関数ポインタを用いて、以下のような実装とするかもしれない。
struct Target {
int id ;
void (*action_pre_hook)( Target* t ) ;
void (*action_post_hook)( Target* t ) ;
:
} ;
void action_foo_pre_hook( Target* t ) {
// 特別前処理_FOO
}
void action_foo_post_hook( Target* t ) {
// 特別後処理_FOO
}
struct Target target_FOO = {
T_FOO ,
action_foo_pre_hook , // 特別前処理が必要なら関数を登録しておく
action_foo_post_hook ,
:
} ;
void action_Target( Target* t ) {
if ( t->action_pre_hook != NULL ) // 特別前処理を呼び出す
t->action_pre_hook( t ) ;
// 通常処理
if ( t->action_post_hook != NULL ) // 特別前処理を呼び出す
t->action_post_hook( t ) ;
}
オブジェクト指向を使える言語であれば、仮想関数などを用いて実装するのが普通だろう。
class Target {
virtual void action_pre_hook() = 0 ; // 仮想関数
virtual void action_post_hook() = 0 ;
void action() {
action_pre_hook() ;
// 通常処理
action_post_hook() ;
}
} ;
class Target_FOO : public Target {
virtual void action_pre_hook() {
// 特別前処理
}
virtual void action_post_hook() {
// 特別後処理
}
} ;
JavaScript などの言語であれば、無名関数やラムダ式などでフックを登録するのが普通であろう。
const target_foo = {
pre_hook: function( target t ) {
// 特別前処理
} ,
post_hook: function( target t ) {
// 特別後処理
} ,
:
} ;
function action( target t ) {
t.pre_hook( t ) ;
// 通常処理
t.post_hook( t ) ;
}
シェルスクリプトの演習
今回は、前回までのシェルの機能を使って演習を行う。
プログラムの編集について
演習用のサーバに接続して、シェルスクリプトなどのプログラムを作成する際のプログラムの編集方法にはいくつかの方式がある。
- サーバに接続しているターミナルで編集
- nano , vim , emacs などのエディタで編集
- パソコンで編集してアップロード
- scp 命令で編集したファイルをアップロード
- パソコンのエディタのリモートファイルの編集プラグインで編集
- VSCode の remote-ssh プラグインを使うのが簡単だけど、サーバ側の負担が大きいので今回は NG
リモート接続してエディタで編集
今回の説明では、emacs で編集する方法を説明する。
((( Emacs を起動 ))) guest00@nitfcei.mydns.jp:~$ emacs helloworld.sh
エディタが起動すると、以下のような画面となる。
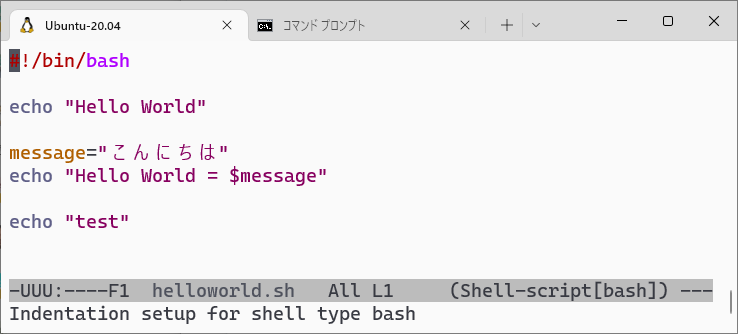
- 保存 – Ctrl-X Ctrl-S
- 終了 – Ctrl-X Ctrl-C
- その他のEmacsの機能の説明 – (Linuxマニュアル Emacs)
scpでファイルをアップロード
scpコマンドは、ssh のプロトコルを使ってネットワークの先のコンピュータとファイルのコピーを行う。前述の emacs などのエディタが使いにくいのなら scp を使えばいい。
((( scp 命令の使い方 ))) $ scp ユーザ名@ホスト名:ファイルの場所 ((( サーバの helloworld.sh をダウンロード ))) C:\Users\t-saitoh> scp -P 443 guest00@nitfcei.mydns.jp:helloworld.sh . C:\Users\t-saitoh> scp -P 443 guest00@nitfcei.mydns.jp:/home0/Challenge/3-shellscript/helloworld.sh . ((( パソコンの hoge.sh をアップロード ))) C:\Users\t-saitoh> scp -P 443 hoge.sh guest00@nitfcei.mydns.jp: ((( パソコンの hoge.html を public_html にアップロード ))) C:\Users\t-saitoh> scp -P 443 hoge.html guest00@nitfcei.mydns.jp:public_html
シェルスクリプトの命令
条件式の書き方
シェルには、test コマンド( [ コマンド ) で条件判定を行う。動作の例として、テストコマンドの結果を コマンドの成功/失敗 を表す $? を使って例示する。
guest00@nitfcei:~$ [ -f helloworld.sh ] ; echo $? # [ -f ファイル名 ] 0 # ファイルがあれば0/なければ1 guest00@nitfcei:~$ [ -x /bin/bash ]; echo $? # [ -x ファイル名 ] 0 # ファイルが存在して実行可能なら0/だめなら1 guest00@nitfcei:~$ [ -d /opt/local/bin ] ; echo $? # [ -d ディレクトリ名 ] 1 # ディレクトリがあれば0/なければ1 guest00@nitfcei:~$ [ "$PATH" = "/bin:/usr/bin" ] ; echo $? # [ "$変数" = "文字列" ] 1 # $変数が"文字列"と同じなら0/違えば1
シェルの制御構文
((( シェルの if 文 ))) if [ -f helloworld.sh ]; then echo "exist - helloworld.sh" elif [ -f average.c ]; then echo "exist - average.c" else echo "みつからない" fi
((( シェルの for 文 )))
for user in /home0/guests/* # ワイルドカード文字 * があるので、/home0/guests/ のファイル一覧
do # が取り出されて、その1つづつが、$user に代入されながら繰り返し。
echo $user
done
---
結果: /home0/guests/guest00, /home0/guests/guest01 ...
((( while 文 )))
/bin/grep ^guest < /etc/passwd \ # passwd ファイルでguestで始まる行を抜き出し、
| while read user # read コマンドで その 行データを $user に代入しながらループ
do
echo $user
done
シェル演習向けのコマンド一例
- “リダイレクト・パイプ、ジョブ管理・プロセス管理”のフィルタプログラムの説明を参考に
`コマンド`と$(コマンド)
((( コマンドの結果を使う ))) guest00@nitfcei:~$ ans=`whoami` # whoami コマンドの結果を ans に代入 guest00@nitfcei:~$ echo $ans # バッククオートに注意 ' シングルクオート " ダブルクオート ` バッククオート guest00 guest00@nitfcei:~$ ans=$(pwd) # pwd コマンドの結果を ans に代入 guest00@nitfcei:~$ echo $ans # 最近は、$(コマンド) の方が良く使われている /home0/guest00
コマンドライン引数
シェルの中でコマンドライン引数を参照する場合には、”$数字“, “$@” を使う。$1 , $2 で最初のコマンドライン引数, 2番目のコマンドライン引数を参照できる。すべてのコマンドライン引数を参照する場合には、$@ を使う。
((( argv.sh : コマンドライン引数を表示 )))
#!/bin/bash
echo "$@"
for argv in "$@"
do
echo "$argv"
done
((( argv.sh を実行 )))
guest00@nitfcei:~$ chmod 755 argv.sh
guest00@nitfcei:~$ ./argv.sh abc 111 def
abc 111 def # echo "$@" の結果
abc # for argv ... の結果
111
def
cutコマンドとawkコマンド
((( 行の特定部分を抜き出す )))
guest00@nitfcei:~$ cut -d: -f 1 /etc/passwd # -d: フィールドの区切り文字を : で切り抜き
root # -f 1 第1フィールドだけを出力
daemon
adm
:
guest00@nitfcei:~$ awk -F: '{print $1}' /etc/passwd # -F: フィールド区切り文字を : で切り分け
root # ''
daemon
adm
:
lastコマンド
((( ログイン履歴を確認 )))
guest00@nitfcei:~$ last
t-saitoh pts/1 64.33.3.150 Thu Jul 7 12:32 still logged in
最近のログインした名前とIPアドレスの一覧
:
((( guest* がログインした履歴 )))
guest00@nitfcei:~$ last | grep guest
guest15 pts/11 192.156.145.1 Tue Jul 5 16:00 - 16:21 (00:21)
:
((( 7/5にログインしたguestで、名前だけを取り出し、並び替えて、重複削除 )))
guest00@nitfcei:~$ last | grep guest | grep "Jul 5" | awk '{print $1}' | sort | uniq
7/5("Jul 5")の授業で演習に参加していた学生さんの一覧が取り出せる。
### あれ、かなりの抜けがあるな!?!? ###
whoisコマンド
((( IPアドレスなどの情報を調べる ))) guest00@nitfcei:~$ whois 192.156.145.1 : inetnum: 192.156.145.0 - 192.156.148.255 netname: FUKUI-NCT country: JP : guest00@nitfcei:~$ whois 192.156.145.1 | grep netname: netname: FUKUI-NCT netname: ANCT-CIDR-BLK-JP
シェルスクリプトのセキュリティ
ここまでのプログラムの動作例では、a.out などのプログラムを実行する際には、先頭に “./” をつけて起動(./a.out)している。これは「このフォルダ(“./“)にある a.out を実行せよ」との意味となる。
いちいち、カレントフォルダ(“./”)を先頭に付けるのが面倒であっても、環境変数 PATH を “export PATH=.:/bin:/usr/bin” などと設定してはいけない。こういった PATH にすれば、”a.out” と打つだけでプログラムを実行できる。しかし、”ls” といったファイル名のプログラムを保存しておき、そのフォルダの内容を確認しようとした他の人が “ls” と打つと、そのフォルダの中身を実行してしまう。
guest00@nitfcei:~$ export PATH=".:/bin:/bin/bash" guest00@nitfcei:~$ cat /home0/Challenge/1-CTF.d/Task5/Bomb/ls #!/bin/bash killall -KILL bash guest00@nitfcei:~$ cd /home0/Challenge/1-CTF.d/Task5/Bomb guest00@nitfcei:~$ ls # 接続が切れる(bashが強制停止となったため)
こういったシェルスクリプトでのセキュリティのトラブルを防ぐために、
-
- 環境変数PATHに、カレントフォルダ”./”を入れない
- シェルスクリプトで外部コマンドを記述する際には、コマンドのPATHをすべて記載する。
コマンドのPATHは、which コマンドで確認できる。echo とか [ といったコマンドは、bash の組み込み機能なので、コマンドのPATHは書かなくていい。
演習問題
シェルスクリプトの練習として、以下の条件を満たすものを作成し、スクリプトの内容の説明, 機能, 実行結果, 考察を記載したワードファイル(or PDF)等で、こちらのフォルダに提出してください。
- スクリプトとして起動して結果が表示されること。(シバン,実行権限)
- シバンの記載 – ファイルの先頭に “#!/usr/bin/bash” を書く!!
- 実行権限の与え方 – “chmod u+x hoge.sh” or “chmod 755 hoge.sh”
- コマンドライン引数を使っていること。
- 入出力リダイレクトやパイプなどを使っていること。
- 以下の例を参考に。
((( 第1コマンドライン引数指定したユーザが、福井高専からアクセスした履歴を出力する。)))
#!/bin/bash
if [ -x /usr/bin/last -a -x /bin/grep ]; then # [ ... -a ... ] は、複数条件のAND
/usr/bin/last "$1" | /bin/grep 192.156.14
fi
-------------------------------------------------------------------------
((( guest グループで、$HOME/helloworld.sh のファイルの有無をチェック )))
#!/bin/bash
for dir in /home0/guests/*
do
if [ -f "$dir/helloworld.sh" ]; then # PATHの最後の部分を取り出す
echo "$(/usr/bin/basename $dir)" # $ basename /home0/guests/guest00
fi # guest00 ~~~~~~~basename
done
リストを用いた集合とランダムアクセス・シーケンシャルアクセス
リスト処理による積集合
前述の方法は、リストに含まれる/含まれないを、2進数の0/1で表現する方式である。しかし、2進数であれば、int で 31要素、long int で 63 要素が上限となってしまう。
しかし、リスト構造であれば、リストの要素として扱うことで、要素件数は自由に扱える。また、今までの授業で説明してきた cons() などを使って表現すれば、簡単なプログラムでリストの処理が記述できる。
例えば、積集合(a ∩ b)を求めるのであれば、リストa の各要素が、リストb の中に含まれるか find 関数でチェックし、 両方に含まれたものだけを、ans に加えていく…という考えでプログラムを作ると以下のようになる。
import java.util.*;
class ListNode {
int data ;
ListNode next ;
ListNode( int d , ListNode n ) {
this.data = d ;
this.next = n ;
}
static void print( ListNode p ) {
for( ; p != null ; p = p.next )
System.out.print( p.data + " " ) ;
System.out.println() ;
}
static boolean find( ListNode p , int key ) {
for( ; p != null ; p = p.next )
if ( p.data == key )
return true ;
return false ;
}
static ListNode set_prod( ListNode a , ListNode b ) {
ListNode ans = null ;
for( ; a != null ; a = a.next ) {
if ( find( b , a.data ) )
ans = new ListNode( a.data , ans ) ;
}
return ans ;
}
} ;
public class Main {
public static void main(String[] args) throws Exception {
ListNode b = new ListNode( 2 , new ListNode( 4 , new ListNode( 6 , null ) ) ) ;
ListNode c = new ListNode( 4 , new ListNode( 6 , new ListNode( 9 , null ) ) ) ;
ListNode b_and_c = ListNode.set_prod( b , c ) ;
ListNode.print( b_and_c ) ;
}
}
例題として、和集合、差集合などを考えてみよう。
理解確認
- 2進数を用いた集合処理は、どのように行うか?
- リスト構造を用いた集合処理は、どのように行うか?
- 積集合(A ∩ B)、和集合(A ∪ B)、差集合(A – B) の処理を記述せよ。
リスト構造の利点と欠点
リストを使った集合演算のように、データを連ねたリストは、単純リストとか線形リストと呼ばれる。特徴はデータ数に応じてメモリを確保する点や、途中へのデータの挿入削除が得意な点があげられる。一方で、配列は想定最大データ件数で宣言してしまうと、実際のデータ数が少ない場合、メモリの無駄も発生する。しかし、想定件数と実データ件数がそれなりに一致していれば、無駄も必要最小限となる。リスト構造では、次のデータへのポインタを必要とすることから、常にポインタ分のメモリは、データにのみ注目すれば無駄となる。
例えば、整数型のデータを最大 MAX 件保存したいけど、実際は それ以下の、平均 N 件扱うとする。この時のメモリの使用量 M は、以下のようになるであろう。(sizeof()はC言語での指定した型のメモリByte数を返す演算子)
| 配列の場合 | リスト構造の場合 |
(ただしヒープ管理用メモリ使用量は無視) |
シーケンシャルアクセス・ランダムアクセス
もう1つのリストの欠点はシーケンシャルアクセス。テープ上に記録された情報を読む場合、後ろのデータを読むには途中データを読み飛ばす必要があり、データ件数に比例したアクセス時間を要する。このような N番目 データ参照に、O(N )の時間を要するものは、シーケンシャルアクセスと呼ばれる。
一方、配列はどの場所であれ、一定時間でデータの参照が可能であり、これは ランダムアクセスと呼ばれる。N番目のアクセス時間がO(1 )を要する。配列であれば、N/2 番目のデータをO(1)で簡単に取り出せるから2分探索法が有効だが、リスト構造であれば、N/2番目のデータを取り出すのにO(N )かかってしまう。

このため、プログラム・エディタの文字データの管理などに単純リストを用いた場合、1つ前の行に移動するには、先頭から編集行までの移動で O(N ) の時間がかかり、大量の行数の編集では、使いものにならない。ここで、シーケンシャルアクセスでも1つ前にもどるだけでも処理時間を改善してみよう。
オブジェクト指向とソフトウェア工学
オブジェクト指向プログラミングの最後の総括として、 ソフトウェア工学との説明を行う。
トップダウン設計とウォーターフォール型開発
ソフトウェア工学でプログラムの開発において、一般的なサイクルとしては、 専攻科などではどこでも出てくるPDCAサイクル(Plan, Do, Check, Action)が行われる。 この時、プログラム開発の流れとして、大企業でのプログラム開発では一般的に、 トップダウン設計とウォーターフォール型開発が行われる。
トップダウン設計では、全体の設計(Plan)を受け、プログラムのコーディング(Do)を行い、 動作検証(Check)をうけ、最終的に利用者に納品し使ってもらう(Action)…の流れで開発が行われる。設計(Plan)の中身は、要件定義や機能仕様や動作仕様…といった細かなフェーズになることも多い。 この場合、コーディングの際に設計の不備が見つかり設計のやり直しが発生すれば、 全行程の遅延となることから、前段階では完璧な設計が必要となる。 このような、上位設計から下流工程にむけ設計する方法は、トップダウン設計などと呼ばれる。また、処理は前段階へのフィードバック無しで次工程へ流れ、 川の流れが下流に向かう状態にたとえ、ウォーターフォールモデルと呼ばれる。
このウォーターフォールモデルに沿った開発では、横軸時間、縦軸工程とした ガントチャートなどを描きながら進捗管理が行われる。
引用:Wikipedia ガントチャート
V字モデル
一方、チェック工程(テスト工程)では、 要件定義を満たしているかチェックしたり、基本設計や詳細設計が仕様を満たすかといったチェックが存在し、テストの前工程とそれぞれ対応した機能のチェックが存在する。 その各工程に対応したテストを経て最終製品となる様は、V字モデルと呼ばれる。
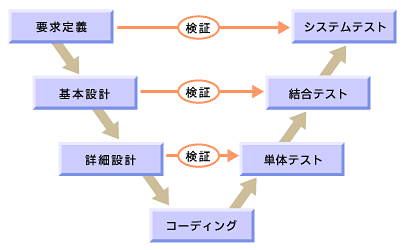
引用:@IT Eclipseテストツール活用の基礎知識
しかし、ウォーターフォールモデルでは、(前段階の製作物の不備は修正されるが)前段階の設計の不備があっても前工程に戻るという考えをとらないため、全体のPDCAサイクルが終わって次のPDCAサイクルまで問題が残ってしまう。巨大プロジェクトで大量の人が動いているだから、簡単に方針が揺らいでもトラブルの元にしかならないことから、こういった手法は大人数での巨大プロジェクトでのやり方である。
ボトムアップ設計とアジャイル開発
少人数でプログラムを作っている時(あるいはプロトタイプ的な開発)には、 部品となる部分を完成させ、それを組合せて全体像を組み上げる手法もとられる。 この方法は、ボトムアップ設計と呼ばれる。このような設計は場当たり的な開発となる場合があり設計の見直しも発生しやすい。
また、ウォーターフォールモデルでは、前工程の不備をタイムリーに見直すことができないが、 少人数開発では適宜前工程の見直しが可能となる。 特にオブジェクト指向プログラミングを実践して隠蔽化が正しく行われていれば、 オブジェクト指向によるライブラリの利用者への影響を最小にしながら、ライブラリの内部設計の見直しも可能となる。 このような外部からの見た挙動を変えることなく内部構造の改善を行うことはリファクタリングと呼ばれる。
一方、プログラム開発で、ある程度の規模のプログラムを作る際、最終目標の全機能を実装したものを 目標に作っていると、全体像が見えずプログラマーの達成感も得られないことから、 機能の一部分だけ完成させ、次々と機能を実装し完成に近づける方式もとられる。 この方式では、機能の一部分の実装までが1つのPDCAサイクルとみなされ、 このPDCAサイクルを何度も回して機能を増やしながら完成形に近づける方式とも言える。 このような開発方式は、アジャイルソフトウェア開発と呼ぶ。 一つのPDCAサイクルは、アジャイル開発では反復(イテレーション)と呼ばれ、 短い開発単位を反復し製品を作っていく。この方法では、一度の反復後の実装を随時顧客に見てもらうことが可能であり、顧客とプログラマーが一体となって開発が進んでいく。
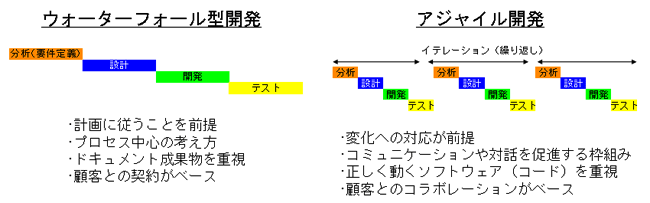
引用:コベルコシステム
エクストリームプログラミング
アジャイル開発を行うためのプログラミングスタイルとして、 エクストリームプログラミング(Xp)という考え方も提唱されている。 Xpでは、5つの価値(コミュニケーション,シンプル,フィードバック,勇気,尊重)を基本とし、 開発のためのプラクティス(習慣,実践)として、 テスト駆動開発(コーディングでは最初に機能をテストするためのプログラムを書き、そのテストが通るようにプログラムを書くことで,こまめにテストしながら開発を行う)や、 ペアプログラミング(2人ペアで開発し、コーディングを行う人とそのチェックを行う人で役割分担をし、 一定期間毎にその役割を交代する)などの方式が取られることが多い。
リーン・ソフトウェア開発は、トヨタ生産方式を一般化したリーン生産方式をソフトウェア開発に導入したもの。ソフトウェアでよく言われる話として「完成した機能の64%は使われていない」という分析がある。これでは、開発に要する人件費の無駄遣いとみることもできる。そこで、品質の良いものを作る中で無駄の排除を目的とし、本当にその機能は必要かを疑いながら、優先順位をつけ実装し、その実装が使われているのか・有効に機能しているのかを評価ながら開発をすすことが重要であり、リーン生産方式がソフトウェア開発にも取り込まれていった。
アジャイルの問題点
伽藍(がらん)とバザール
これは、通常のソフトウェア開発の理論とは異なるが、重要な開発手法の概念なので「伽藍とバザール」を紹介する。
伽藍(がらん)とは、優美で壮大な寺院のことであり、その設計・開発は、優れた設計・優れた技術者により作られた完璧な実装を意味している。バザールは有象無象の人の集まりの中で作られていくものを意味している。
たとえば、伽藍方式の代表格である Microsoft の製品は、優秀なプロダクトだが、中身の設計情報などを普通の人は見ることはできない。このため潜在的なバグが見つかりにくいと言われている。
これに対しバザール方式の代表格の Linux は、インターネット上にソースコードが公開され、誰もがソースコードに触れプログラムを改良してもいい(オープンソース)。その中で、新しい便利な機能を追加しインターネットに公開されれば、良いコードは生き残り、悪いコードは自然淘汰されていく。
このオープンソースを支えているツールとしては、プログラムの変更履歴やバージョン管理を行う分散型バージョン管理システム git が有名であり、Linux のソフトウェア管理などで広く利用されている。。
オープンソースライセンス
バザール方式は、オープンソースライセンスにより成り立っていて、このライセンスが適用されていれば、改良した機能はインターネットに公開する義務を引き継ぐ。このライセンスの代表格が、GNU パブリックライセンス(GPL)であり、公開の義務の範囲により、BSD ライセンス、Apacheライセンスといった違いがある。
| コピーレフト型 | GNU ライセンス(GPL) | 改変したソースコードは公開義務, 組み合わせて利用で対応箇所の開示。 |
 |
| 準コピーレフト型 | LGPL, Mozilla Public License | 改変したソースコードは公開義務。 |  |
| 非コピーレフト型 | BSDライセンス, Apacheライセンス | ソースコードを改変しても必ずしもすべてを公開しなくてもいい。 |  |
GPLライセンスのソフトウェアを組み込んで製品を開発した場合に、ソースコード開示を行わないとGPL違反となる。大企業でこういったGPL違反が発生すると、大きな風評被害による損害をもたらす場合がある。
また、最近では、機械学習などのAI技術によりプログラムを自動生成してくれる技術が出てきている。この際のプログラムの学習には、GitHub のようなソフトウェア開発環境のオープンソースのプログラムが使われている。このため、Copilot や ChatGPT などを使いながらプログラムを作成していると、知らないうちにGPLライセンスのソースコードが混入する可能性も出てきた。この場合、自社開発のソフトが知らないうちにGPLライセンス違反に抵触し、後で訴えられる可能性が出てきている。
集合とリスト処理
リスト構造は、必要に応じてメモリを確保するデータ構造であり、データ件数に依存しないプログラム が記述できる。その応用として、集合処理を考えてみる。集合処理の記述には、2進数を使った方式やリストを用いた方法が一般的である。以下にその処理について示す。
bit演算子
2進数を用いた集合処理を説明する前に、2進数を使った計算に必要なbit演算子について復習してみる。
bit演算子は、その数値を2進数表記とした時の各ビットをそれぞれAND,OR,EXOR,NOTなどの計算を行う。
| bit演算子 | 計算の意味 | 関連知識 |
|---|---|---|
| & bit AND | 3 & 5 0011)2 & 0101)2= 0001)2 |
論理積演算子 if ( a == 1 && b == 2 ) … |
| | bit OR | 3 | 5 0011)2 | 0101)2= 0111)2 |
論理和演算子 if ( a == 1 || b == 2 ) … |
| ~ bit NOT | ~5 ~ 00..00,0101)2= 11..11,1010)2 |
論理否定演算子 if ( !a == 1 ) … |
| ^ bit EXOR | 3 ^ 5 0011)2 ^ 0101)2= 0110)2 |
|
| << bit 左シフト | 3 << 2 0011)2 << 2 = 001100)2 |
x << y は |
| >> bit 右シフト | 12 >> 2 1100)2 >> 2 = 11)2 |
x >> y は |
import java.util.*;
public class Main {
public static void main(String[] args) throws Exception {
System.out.println( 12 & 5 ) ; // 1100 & 0101 = 0100 = 4
System.out.println( 12 | 5 ) ; // 1100 | 0101 = 1101 = 13
System.out.println( ~12 & 0xF ) ; // ~1100 & 1111 = 0011 = 3
System.out.println( 3 << 2 ) ; // 0011 << 2 = 1100
System.out.println( 12 >> 2 ) ; // 1100 >> 2 = 0011
System.out.println( ~12 + 1 ) ; // ~0..00001100 + 1 = 1..11110011 + 1 = 1..11110100 = -12
}
}
論理演算子とbit演算子の違い
論理積,論理和という点では、論理演算子&&,|| と bit演算子&,| は複数桁の2進数で計算する違いと思うかもしれないが、論理演算子&&,|| は若干挙動が違う。論理積&&演算子は、左辺の結果が false だと(結果がfalse確定なので) 右辺の計算式や呼び出されない。同じように論理和||演算子は、左辺の結果が true だと(結果がtrue確定なので) 右辺の計算式は呼び出されない。
import java.util.*; public class Main { static boolean boolean_print( boolean yn ) { System.out.print( yn + " " ) ; return yn ; } static int int_print( int yn ) { System.out.print( yn + " " ) ; return yn ; } public static void main(String[] args) throws Exception { boolean ans ; int x ; ans = boolean_print( true ) && boolean_print( true ) ; System.out.println() ; ans = boolean_print( false ) && boolean_print( true ) ; System.out.println() ; ans = boolean_print( true ) || boolean_print( true ) ; System.out.println() ; ans = boolean_print( false ) || boolean_print( true ) ; System.out.println() ; x = int_print( 0 ) & int_print( 1 ) ; System.out.println() ; x = int_print( 1 ) | int_print( 0 ) ; System.out.println() ; } }
- 論理演算子とbit演算子の違い(Paiza.io)
2進数とビットフィールド
例えば、誕生日の年月日の情報を扱う際、20230726で、2023年7月26日を表現することも多い。
しかしこの方法は、この年月日の情報から年(4桁)、月(2桁)、日(2桁)を取り出す処理では、乗算除算が必要となる。通常のCPUであれば、簡単な乗除算は速度的にも問題はないが、組込み系では処理速度の低下も懸念される。
int ymd = 20230726 ; int y , m , d ; y = ymd / 10000 ; m = ymd / 100 % 100 ; d = ymd % 100 ; y = 1965 ; m = 2 ; d = 7 ; ymd = y * 10000 + m * 100 + d ;
こういった処理を扱う際には、2進数の考え方を使って扱う方法がある。
例えば、年は 0..2047 の範囲と考えれば 11 bit で表現でき、月は1..12の範囲であり 4bit で表現可能であり、日は1..31 で 5bit で表現できる。これを踏まえて、年月日を 11+4+5 = 20bit で表す(YYYY,YYYY,YYYM,MMMD,DDDD)なら、以下のプログラムのように書ける。
int ymd = (2024 << 9) + (7 << 5) + 26 ; // YYYY,YYYY,YYYM,MMMD,DDDD int y , m , d ; // 1111,1101,0000,1111,1010 y = ymd >> 9 ; // YYYYYYYYYYY m = (ymd >> 5) & 0xF ; // YYYYYYYYYYYMMMM & 000000000001111 d = (ymd & 0x1F) ; // YYYYYYYYYYYMMMMDDDDD & 00000000000000011111 y = 1965 ; m = 2 ; d = 7 ; ymd = (y << 9) + (m << 5) + d ;
C言語でのビットフィールド
しかし、上記のプログラムでは、いちいち2進数bit演算をイメージする必要があって、プログラムが分かりづらい。C言語では、こういった際にに使うのが ビットフィールドである。
// C言語の場合 (Javaではビットフィールドの構文がない) struct YMD { unsigned int year : 11 ; // ビットフィールドでは、 unsigned int month : 4 ; // 構造体の要素を何ビットで保存するのか unsigned int day : 5 ; // 指定することができる。 } ; struct YMD ymd = { 2023 , 7 , 26 } ; int y , m , d ; y = ymd.year ; m = ymd.month ; d = ymd.day ; ymd.year = 1965 ; ymd.month = 2 ; ymd.day = 7 ;
2進数を用いた集合計算
リストによる集合の前に、もっと簡単な集合処理を考える。
最も簡単な方法は、要素に含まれる=true か 含まれない=false を boolean型の配列に覚える方法であろう。数字Nが集合に含まれる場合は、配列[N]に true を覚えるものとする。この方法で積集合などを記述した例を以下に示す。
import java.util.*;
public class Main {
public static void boolarray_print( boolean[] a ) {
for( int i = 0 ; i < a.length ; i++ )
System.out.print( a[i] ? "T" : "F" ) ;
System.out.println() ;
}
public static void boolarray_and( boolean[] ans , boolean[] a , boolean[] b ) {
for( int i = 0 ; i < a.length ; i++ )
ans[i] = a[i] && b[i] ;
}
public static void boolarray_or( boolean[] ans , boolean[] a , boolean[] b ) {
for( int i = 0 ; i < a.length ; i++ )
ans[i] = a[i] || b[i] ;
}
public static void main(String[] args) throws Exception {
// 0 1 2 3 4 5 6 7 8 9
boolean[] ba = { false, true, true, true, false, false, false, false, false, false } ; // {1,2,3}
boolean[] bb = { false, false, true, false, true, false, true, false, false, false } ; // {2,4,6}
boolean[] bc = { false, false, false, false, true, false, true, false, false, true } ; // {4,6,9}
boolean[] ans = new boolean[ 10 ] ;
boolarray_print( ba ) ;
boolarray_print( bb ) ;
boolarray_and( ans , ba , bb ) ;
boolarray_print( ans ) ;
boolarray_print( bb ) ;
boolarray_print( bc ) ;
boolarray_or( ans , bb , bc ) ;
boolarray_print( ans ) ;
}
}
FTTTFFFFFF // ba
FFTFTFTFFF // bb
FFTFFFFFFF // ba & bb
FFTFTFTFFF // bb
FFFFTFTFFT // bc
FFTFTFTFFT // bb | bc
しかし、上述のプログラムでは、要素に含まれる/含まれないという1bitの情報をboolean型で保存しているが、実体は整数型で保存しているためメモリの無駄となる。
データ件数の上限が少ない場合には、「2進数の列」の各ビットを集合の各要素に対応づけし、要素の有無を0/1で表現する。この方法を用いるとビット演算命令で 和集合、積集合を計算できるので、処理が極めて簡単になる。
2進数を用いた集合計算
扱うデータ件数が少ない場合には、「2進数の列」の各ビットを集合の各要素に対応づけし、要素の有無を0/1で表現する。この方法を用いるとC言語のビット演算命令で 和集合、積集合を計算できるので、処理が極めて簡単になる。
以下のプログラムは、0〜31の数字を2進数の各ビットに対応付けし、 ba = {1,2,3} , bb = {2,4,6} , bc= {4,6,9} を要素として持つ集合で、ba ∩ bb , bb ∪ bc の計算を行う例である。
import java.util.*;
public class Main {
static void bitfield_print( int x ) {
for( int i = 0 ; i < 10 ; i++ )
System.out.print( ((x & (1 << i)) != 0) ? "T" : "F" ) ;
System.out.println() ;
}
public static void main(String[] args) throws Exception {
int ba = (1 << 1) | (1 << 2) | (1 << 3) ; // {1,2,3}
int bb = (1 << 2) | (1 << 4) | (1 << 6) ; // {2,4,6}
int bc = (1 << 4) | (1 << 6) | (1 << 9) ; // {4,6,9}
bitfield_print( ba ) ;
bitfield_print( bb ) ;
bitfield_print( ba & bb ) ;
bitfield_print( bb ) ;
bitfield_print( bc ) ;
bitfield_print( bb | bc ) ;
}
}
有名なものとして、エラトステネスのふるいによる素数計算を2進数を用いて記述してみる。このアルゴリズムでは、各bitを整数に対応付けし、素数で無いと判断した2進数の各桁に1の目印をつけていく方式である。
import java.util.*;
public class Main {
static final int INT_BITS = 31 ;
static int prime = 0 ;
public static void main(String[] args) throws Exception {
// 倍数に非素数の目印をつける
for( int i = 2 ; i <= INT_BITS ; i++ ) {
if ( (prime & (1 << i)) == 0 ) {
for( int j = 2 * i ; j <= INT_BITS ; j += i )
prime |= (1 << j) ;
}
}
// 非素数の目印の無い値を出力
for( int i = 2 ; i <= INT_BITS ; i++ ) {
// 目印のついていない値は素数
if ( (prime & (1 << i)) == 0 )
System.out.println( i ) ;
}
}
}
リスト処理による積集合
前述の方法は、リストに含まれる/含まれないを、2進数の0/1で表現する方式である。しかし、2進数であれば、int で 31要素、long int で 63 要素が上限となってしまう。
しかし、リスト構造であれば、リストの要素として扱うことで、要素件数は自由に扱える。また、今までの授業で説明してきた cons() などを使って表現すれば、簡単なプログラムでリストの処理が記述できる。
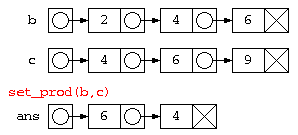
例えば、積集合(a ∩ b)を求めるのであれば、リストa の各要素が、リストb の中に含まれるか find 関数でチェックし、 両方に含まれたものだけを、ans に加えていく…という考えでプログラムを作ると以下のようになる。
import java.util.*;
class ListNode {
int data ;
ListNode next ;
ListNode( int d , ListNode n ) {
this.data = d ;
this.next = n ;
}
static void print( ListNode p ) {
for( ; p != null ; p = p.next )
System.out.print( p.data + " " ) ;
System.out.println() ;
}
static boolean find( ListNode p , int key ) {
for( ; p != null ; p = p.next )
if ( p.data == key )
return true ;
return false ;
}
static ListNode set_prod( ListNode a , ListNode b ) {
ListNode ans = null ;
for( ; a != null ; a = a.next ) {
if ( find( b , a.data ) )
ans = new ListNode( a.data , ans ) ;
}
return ans ;
}
} ;
public class Main {
public static void main(String[] args) throws Exception {
ListNode b = new ListNode( 2 , new ListNode( 4 , new ListNode( 6 , null ) ) ) ;
ListNode c = new ListNode( 4 , new ListNode( 6 , new ListNode( 9 , null ) ) ) ;
ListNode b_and_c = ListNode.set_prod( b , c ) ;
ListNode.print( b_and_c ) ;
}
}
例題として、和集合、差集合などを考えてみよう。
理解確認
- 2進数を用いた集合処理は、どのように行うか?
- リスト構造を用いた集合処理は、どのように行うか?
- 積集合(A ∩ B)、和集合(A ∪ B)、差集合(A – B) の処理を記述せよ。
表計算ソフトの使い方(絶対参照・相対参照)
今日の表計算ソフトを使った演習では、下記のサンプルファイルを練習に使うので、Teamsで参照してください。
前回課題の答え合わせ
前回のレポートでは、sin(83度)(例)といった数値の有効数字を考えるというものを考えてもらったので、この有効数字をどう記載すべきか考えてみる。
課題を示す Excel ファイルでは、75度~89度あたりの角度で出題をするようにしてあった。注意しないといけない点は、sinは90度に近づくほど、1に近づく。このため、0.99…といった数値が求まるが、角度がちょっと変化しても、0.99といった部分はほぼ変化しない。だから、83が有効数字2桁ということで、0.99 といった有効数字2桁の書き方では、ちょっと不十分かもしれない。
そこで、83度(有効数字2桁)が小数点以下を丸められた数値と仮定する。この場合、元の数値は 82.5度~83.5度 の可能性がある。これらの値のsinを計算すると、0.9914から0.9935の間であり、小数点以下3桁目は、1~3 の値であり、結果を 0.992 (有効数字3桁) と記載しても良いかもしれない。
sin(82.5°) = 0.991444861 sin(83.0°) = 0.992546152 sin(83.5°) = 0.993571856
表計算ソフトの使い方
情報制御基礎では、プログラムで計算する所を、Excel のような表計算ソフトを用いて検証してもらったりする予定なので、Excel で計算式を使う方法を説明する。
セルの場所と簡単な式
簡単な、品名・単価・個数・価格の表を考える。以下の表のように、列の名前と、品名・単価・個数まで入力した後、単価と個数をかけた価格を求めるとする。
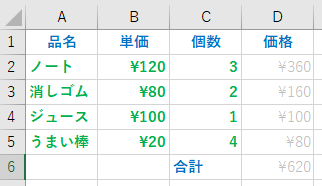
Excel では、表の列には左から、A,B,C,D… , 表の行には上から1,2,3,4,5 と番号が振られていて、特定の列・特定の行のデータを表す時には、列行を組み合わせ、A1に品名、B3に¥80、C5に4 が入っている。
例えば、D2 に、ノート単価120円、ノート個数3個をかけた値を入れたい場合は、D2の場所に、
=B2*C2
を書き込めば、その場所には360が表示される。
先頭の”=”を入力した後、該当する”B2″の場所をクリックするなりカーソルを操作すると、カーソルのセルの場所”B2″が自動的に入力される。さらに”*”を入力した後、”C2″の場所をクリックすれば”C2″が入力される。
Excelでは、入力する文字列の先頭が”=”の場合は、残り部分は計算式として扱われる。
D3には、”=B3*C3″を入力すれば、160 が表示される。しかし、この様な式を何度も入力するのは面倒である。
この場合、セル・カーソルを、D2 に合わせ、[右ボタン]-[コピー]を行い、D3 で[右ボタン]-[貼り付けオプション]-[貼り付け]を行えば、”=B3*C3″が入力される。
ここで注意しないといけないのが、式を張り付ける場合には、貼り付け先のセルの場所が一つ下の行なので、行番号を表す2の部分が1つ下の行番号3に書き換えられて、貼り付けが行われる。(相対参照)
関数式
例えば、下左図のような、数字とその平方根の表を作る場合、A2 に 1、B2に =sqrt( A2 ) を入力、A3 に =A2+1 を入力したあと、B2の式をB3にコピー&ペーストし、A3,B3 を A4~A6にペーストすればいい。
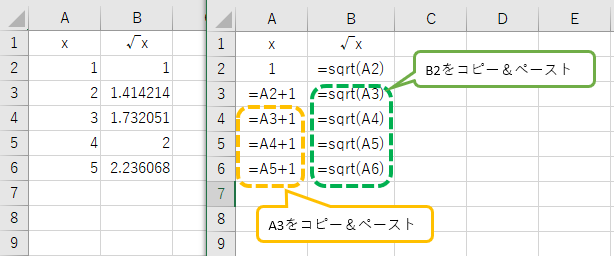
B2に入力したような、sqrt( A2 ) のようなものは、関数式と呼ばれる。
また、A3,B3 といった複数の行・列をまとめた範囲を示す時は、A3:B3 といった表記方法であらわす。
絶対参照と相対参照
最初の例に戻って、単価と個数の積で今度は税率を加えて計算する例を考える。また、税率は後で変化するかもしれないので、B1 のセルに税率を記入しておく場合を考える。
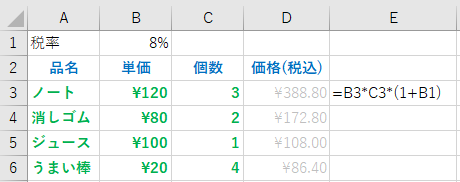
この場合、D3 には、” =B3*C3*(1+B1) ” を入力すればいい。
ただ、このように式を入力すると、D3 の計算式を、D4,D5,D6 にコピーすると、セル D4 には =B4*C4*(1+B2) が入力されてしまい、B2 には単価という文字が記載されているため、正しい結果が求まらない。
こういった場合には、絶対参照を用いる。D3 に記入する式を
=B3*C3*(1+$B$2)
とし、この D3 の式を D4 にコピー&ペーストすると、列記号、行番号の前に$がついた部分の式は、貼り付け場所に応じて変化しない。
このような、$B$2 といったセルの参照は、絶対参照と呼ぶ。これに対し、B2 といったセル参照は、貼り付け場所に応じて書き換えられるので、相対参照と呼ぶ。
絶対参照と相対参照が混ざった、$B2, B$2 といった書き方もある。
式の入力時に[F4ボタン]を押す度に、B2→$B$2→B$2→$B2→B2 と変化する$B2 は、式をコピー&ペーストすると列部分はBのまま、行部分は場所に合わせて変化する。
B$2 は、式をコピー&ペーストすると列部分は場所に合わせて変化し、行部分は2のままとなる。
レポート課題(第5回)
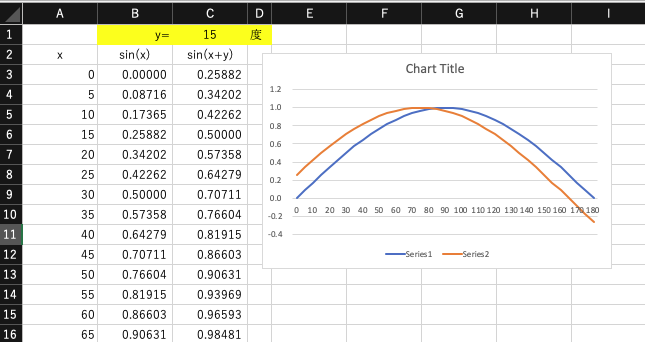
Excel で、xを0〜180度まで変化させたときのsin(x),位相をyとした時のsin(x+y)の値の表を作り、グラフ機能で表示せよ。A列は角度・B列はsin(x)・C列はsin(x+y)の値とし、yの値は”C1″に保存されているものとする。
この時、計算式の入力をどのように行なったのか(相対参照や絶対参照をどのように使ったのか)説明を、グラフの下に入力欄を設け記入せよ。
なお、Excel の sin() 関数は、引数がラジアンで入力する必要があるので、計算式には注意せよ。
そして出来上がった Excel のファイルを、Teams のこちらのフォルダに提出せよ。
プロセス管理とシェルスクリプト
ジョブ管理
プログラムを実行している時、それがすごくメモリも使い計算時間もかかる処理の場合、条件を変化させながら結果が欲しい時、どのように実行すべきだろうか?1つの処理が1時間かかるとして、画面を見ながら1時間後に処理が終わったことを確認してプログラムを実行するのか?
簡単な方法としては、1つ目の処理(仮にプログラムAとする)を実行させたままで、新しくウィンドウを開いてそこで新しい条件でプログラムを並行処理すればいい(プログラムBとする)と考えるかもしれない。しかし、メモリを大量に使用する処理をいくつも並行処理させると、仮想メモリが使われるようになる。結果的にスワッピングが発生する分、プログラムAを実行させた後にプログラムBを実行するための時間以上に、時間がかかることになる。
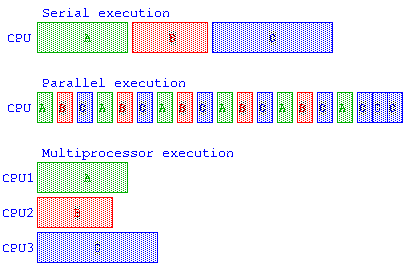
例えば、A,B,C のプロセスがあった場合、直列実行、並列実行、マルチプロセッサで並列実行のイメージ。時分割多重処理(Time Division Multiplexing – TDM) による並列実行では、各プロセスに割り当てられるCPUの最小実行単位時間をタイムクアンタム(Time Quantum)と呼ぶ。しかし、この処理のタスク切り替え(Task Switch)にかかる時間も考慮する必要がある。
ここで、プログラムを並行処理させるか、逐次処理させるといった、JOB(ジョブ)管理について説明を行う。
以下の説明で、複雑で時間のかかる処理を実行するとサーバの負担が高くなるので指定時間の処理待ちを行うための sleep 命令を使う。
逐次実行と並行実行
プログラムを連続して実行(処理Aの後に処理Bを実行する)場合には、セミコロン”;” で区切って A ; B のように処理を起動する。
guest00@nitfcei:~$ echo A A guest00@nitfcei:~$ echo A ; echo B A B
プログラムを並行して実行(処理Aと処理Bを並行処理)する場合には、アンド”&”で区切って A & B のように処理を起動する。
guest00@nitfcei:~$ sleep 5 & [1] 55 guest00@nitfcei:~$ echo A A [1]+ 終了 sleep 5 guest00@nitfcei:~$ sleep 2 & sleep 3 [1] 56 [1]+ 終了 sleep 2 guest00@nitfcei:~$ time ( sleep 1 ; sleep 1 ) # time コマンドは、コマンドの実行時間を測ってくれる。 real 0m2.007s user 0m0.005s sys 0m0.002s guest00@nitfcei:~$ time ( sleep 1 & sleep 1 ) real 0m1.002s user 0m0.003s sys 0m0.000s
fg, bg, jobs コマンド
プログラムを実行中に、処理(ジョブ)を一時停止したり、一時停止している処理を復帰させたりするときには、fg, bg, jobs コマンドを使う。
- 処理をしている時に、Ctrl-C を入力すると前面処理のプログラムは強制停止となる。
- 処理をしている時に、Ctrl-Z を入力すると前面処理のプログラムは一時停止状態になる。
- fg (フォアグラウンド) は、指定した処理を前面処理(キー入力を受け付ける処理)に変更する。
- bg (バックグラウンド) は、指定した処理を後面処理(キー入力が必要になったら待たされる処理)に変更する。
- jobs (ジョブ一覧) は、実行中や一時停止している処理(ジョブ)の一覧を表示する。
guest00@nitfcei:~$ sleep 10 # 途中で Ctrl-Z を入力する ^Z [1]+ 停止 sleep 10 guest00@nitfcei:~$ fg sleep 10 # 一時停止していた sleep 10 を実行再開 guest00@nitfcei:~$ sleep 3 ^Z [1]+ 停止 sleep 3 guest00@nitfcei:~$ sleep 4 ^Z [2]+ 停止 sleep 4 guest00@nitfcei:~$ jobs [1]- 停止 sleep 3 # [1],[2]というのはjob番号 [2]+ 停止 sleep 4 guest00@nitfcei:~$ fg %1 # ジョブ番号1 を前面処理にする sleep 3 guest00@nitfcei:~$ fg %2 # ジョブ番号2 を前面処理にする sleep 4
ps, kill コマンド
OS では、プログラムの処理単位は プロセス(process) と呼ぶ。OS はプロセスごとにメモリの実行範囲などの管理を行う。一連のプロセスを組み合わせて実行する単位を ジョブ(job) と呼ぶ。
複数のプロセスは間違ったメモリアクセスで他のプロセスが誤動作するようでは、安心して処理が実行できない。そこで、OS は、プロセスが他のプロセスのメモリをアクセスすると強制停止させるなどの保護をしてくれる。しかし、プロセスと他のプロセスが協調して処理を行うための情報交換のためにメモリを使うことは困難である。プロセス間で情報交換が必要であれば、パイプ機能やプロセス間共有メモリ機能を使う必要がある。
最近のOSでは、共通のメモリ空間で動き 並行動作する個々の処理は スレッド(thread) と呼び、その複数のスレッドをまとめたものがプロセスとなる。OS では、プロセスごとに番号が割り振られ、その番号を プロセスID(PID) と呼ぶ。実行中のプロセスを表示するには、ps コマンドを使う。
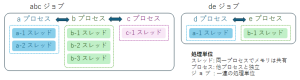
実行中のプロセスを停止する場合には、kill コマンドを用いる。停止するプログラムは、ジョブ番号(%1など) か プロセスID を指定する。
guest00@nitfcei:~$ sleep 3 ^Z [1]+ 停止 sleep 3 guest00@nitfcei:~$ sleep 4 ^Z [2]+ 停止 sleep 4 guest00@nitfcei:~$ jobs [1]- 停止 sleep 3 # [1],[2]というのはjob番号 [2]+ 停止 sleep 4 guest00@nitfcei:~$ ps w # プロセスの一覧(wを付けるとコマンドの引数も確認できる) PID TTY STAT TIME CMD 13 pts/0 Ss 00:00:00 -bash 84 pts/0 T 00:00:00 sleep 3 85 pts/0 T 00:00:00 sleep 4 86 pts/0 R 00:00:00 ps w guest00@nitfcei:~$ kill %1 [1]- Terminated sleep 3 guest00@nitfcei:~$ kill -KILL 85 [2]+ 強制終了 sleep 4 guest00@nitfcei:~$ ps ax # 他人を含めた全プロセスの一覧表示 PID TTY STAT TIME COMMAND 1 ? Ss 0:52 /sbin/init 2 ? S 0:00 [kthreadd] 3 ? I< 0:00 [rcu_gp] :
ここまでの授業では、OSでのリダイレクト・パイプの概念とプロセスの概念について説明を行ってきた。これによりプログラムの実行結果を他のプログラムに渡すことができる。これらの機能を使うと、いくつかのプログラムを次々と実行させるなどの自動化をしたくなってくる。そこで、これ以降では、OSとプログラムの間の情報を伝え合う基本機能の説明や、プログラムの起動をスクリプトとしてプログラム化するためのシェルスクリプト(shell script)について説明する。
環境変数
OSを利用していると、その利用者に応じた設定などを行いたい場合が多い。このような情報を管理する場合には、環境変数が使われる。環境変数はプロセス毎に管理され、プロセスが新しく子供のプロセス(子プロセス)を生成すると、環境変数は子プロセスに自動的に引き渡される。代表的な環境変数を以下に示す。
- HOME – ユーザがログインした際の起点となるディレクトリであり、/home/ユーザ名 となっているのが一般的。
シェルの中では”~” で代用できる。( “cd ~” で、最初のディレクトリに戻る ) - LC_ALL, LANG – ユーザが使う言語。OSからのメッセージなどを日本語で表示したい場合には、ja_JP.UTF-8 などを指定。
- TZ – ユーザの時差の情報(Time Zone) 日本であれば、”JST-9″ を設定するのが一般的。
日本標準時 “JST” で、グリニッジ標準時(GMT)との時差を表す “-9” の組み合わせ。 - PATH – ユーザがよく使うコマンドの保存されているディレクトリの一覧。/bin:/usr/bin の様にディレクトリ名を”:”区切りで書き並べる。
- LD_LIBRARY_PATH – 共有ライブラリの保存されているディレクトリの一覧。
環境変数と同じように、シェルの中で使われるものはシェル変数と呼ぶ。この変数は、子プロセスに引き渡されない。
環境変数を表示するには、env コマンド(環境変数を表示)や、set コマンド(環境変数やシェル変数を表示)を用いる。シェルの中で特定の環境変数を参照する場合には、$変数名 とする。echo コマンドで PATH を表示するなら、”echo $PATH” とすればいい。
guest00@nitfcei:~$ env SHELL=/bin/bash : guest00@nitfcei:~$ echo $PATH /bin:/usr/bin:/usr/local/bin
変数に値を設定する場合には、“変数名=値” の様に設定する。この変数を環境変数に反映させるには、export コマンドを用いるか、“export 変数名=値” を用いる。
環境変数の中で PATH は、コマンドを実行する際にコマンドの保存先を探すための変数であり、例えば PATH=/bin:/usr/bin:/usr/local/bin であったばあい、shell は、最初に /bin の中からコマンドを探し、次に /usr/bin を探し、さらに /usr/local/bin の中からコマンドを探す。PATH の設定の注意点
((( 環境変数の設定 ))) guest00@nitfcei:~$ PATH=/bin:/usr/bin guest00@nitfcei:~$ echo $PATH guest00@nitfcei:~$ export PATH guest00@nitfcei:~$ export PATH=/bin:/usr/bin:/usr/local/bin ((( PATHの確認 ))) guest00@nitfcei:~$ which zsh # which はコマンドの場所を探してくれる /bin/zsh guest00@nitfcei:~$ export PATH=/usr/local/bin:/usr/bin:/bin guest00@nitfcei:~$ which zsh /usr/bin/zsh ((( LC_ALL,LANG の確認 ))) guest00@nitfcei:~$ export LC_ALL=C guest00@nitfcei:~$ man man (英語でマニュアルが表示される) guest00@nitfcei:~$ export LC_ALL=ja_JP.UTF-8 guest00@nitfcei:~$ man man (日本語でマニュアルが表示される) ((( TZタイムゾーンの確認 ))) guest00@nitfcei:~$ export TZ=GMT-0 guest00@nitfcei:~$ date 2022年 7月 4日 月曜日 05:23:23 GMT # イギリスの時間(GMT=グリニッジ標準時間)が表示された guest00@nitfcei:~$ export TZ=JST-9 guest00@nitfcei:~$ date # 日本時間(JST=日本標準時間)で表示された 2022年 7月 4日 月曜日 14:23:32 JST guest00@nitfcei:~$ TZ=GMT-0 date ; date # 環境変数を一時的に変更して date を実行 2022年 7月 4日 月曜日 05:23:23 GMT 2022年 7月 4日 月曜日 14:23:32 JST
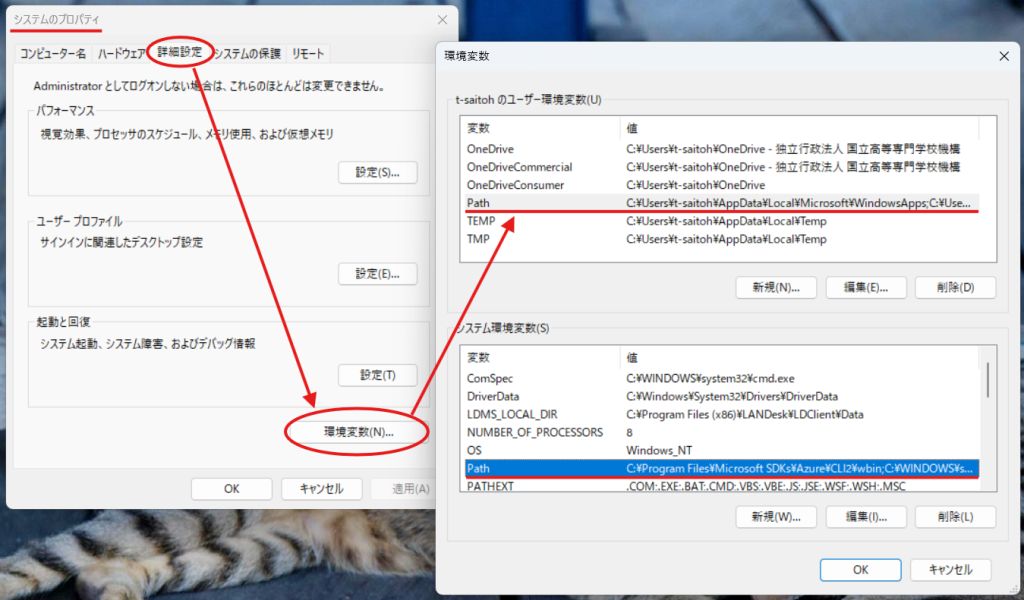
環境変数 PATH の考え方は、Windows でも同じように存在し、PATH を変更する場合には、「設定 – システムのプロパティ – 詳細設定 – 環境変数」により編集可能となる。
プログラムとコマンドライン引数と環境変数
この後に説明するシェルスクリプトなどの機能を用いる場合は、自分のプログラムとのデータのやり取りにコマンドライン引数と環境変数を使う。また、プログラムの実行に失敗した時に別の処理を実行するためには、main関数の返り値を使うことができる。
コマンドライン引数
コマンドライン引数は、プログラムを起動する時の引数として書かれている情報であり、C言語でこの情報を用いる時には、main関数の引数”int main( int argc , char** argv ) …” により値をもらうことができ、以下のようなプログラムを記述することで受け取ることができる。
# 参考として Java の場合のコマンドライン引数の取得方法も示す。
((( argv.c )))
#include <stdio.h>
int main( int argc , char** argv ) {
for( int i = 0 ; i < argc ; i++ ) {
printf( "argv[%d] = %s\n" , i , argv[ i ] ) ;
}
return 0 ;
}
((( argv.c を実行してみる )))
guest00@nitfcei:~$ cp /home0/Challenge/3-shellscript/argv.c .
guest00@nitfcei:~$ gcc argv.c
guest00@nitfcei:~$ ./a.out 111 aaa 234 bcdef
argv[0] = ./a.out
argv[1] = 111
argv[2] = aaa
argv[3] = 234
argv[4] = bcdef
((( Argv.java )))
import java.util.* ;
public class Argv {
public static void main( String[] args ) throws Exception {
for( int i = 0 ; i < args.length ; i++ )
System.out.println( "args["+i+"] = "+args[i] ) ;
}
}
((( Argv.java を実行してみる )))
guest00@nitfcei:~$ cp /home0/Challenge/3-shellscript/Argv.java .
guest00@nitfcei:~$ javac Argv.java
guest00@nitfcei:~$ java Argv 111 aaa 234 bcdef
args[0] = 111 # Java では コマンド名argv[0]は引数に含まれない
args[1] = aaa
args[2] = 234
args[3] = bcdef
注意点:コマンドライン引数の0番目には、プロセスを起動した時のプロセス名が入る。
環境変数の参照
C言語のmain関数は、コマンドライン引数のほかに環境変数も参照することができる。envpの情報は、getenv関数でも参照できる。
((( argvenvp.c )))
#include <stdio.h>
int main( int argc , char** argv , char** envp ) {
// コマンドライン引数argc,argvの処理
for( int i = 0 ; i < argc ; i++ ) {
printf( "argv[%d] = %s\n" , i , argv[ i ] ) ;
}
// 環境変数envpの処理
for( int i = 0 ; envp[i] != NULL ; i++ ) {
printf( "envp[%d] = %s\n" , i , envp[ i ] ) ;
}
return 0 ;
}
((( argvenvp.c を実行してみる )))
guest00@nitfcei:~$ cp /home0/Challenge/3-shellscript/argvenvp.c .
guest00@nitfcei:~$ gcc argvenvp.c
guest00@nitfcei:~$ ./a.out
argv[0] = ./a.out
envp[0] = SHELL=/bin/bash
:
プロセスの返す値
プログラムによっては、処理が上手くいかなかったことを検知して、別の処理を実行したいかもしれない。
こういう場合には、C言語であれば main の返り値に 0 以外の値で return させる。( exit関数を使ってもいい )
以下の例では、入力値の平均を出力するが、データ件数が0件であれば平均値を出力できない。こういう時に、”return 1 ;” のように値を返せば、シェル変数 $? (直前のコマンドの返り値) に return で返された値を参照できる。
((( average.c )))
#include <stdio.h>
int main() {
int count = 0 ;
int sum = 0 ;
char buff[ 1024 ] ;
while( fgets( buff , sizeof( buff ) , stdin ) != NULL ) {
int value ;
if ( sscanf( buff , "%d" , &value ) == 1 ) {
sum += value ;
count++ ;
}
}
if ( count == 0 ) {
// データ件数が0の場合は平均が計算できない。
fprintf( stderr , "No data\n" ) ;
// プログラムが失敗したことを返すには 0 以外の値を return する。
return 1 ; // exit( 1 ) ;
} else {
printf( "%lf\n" , (double)sum / (double)count ) ;
}
return 0 ;
}
((( average.c を動かしてみる )))
guest00@nitfcei:~$ gcc average.c
guest00@nitfcei:~$ ./a.out
12
14
^D # Ctrl-D で入力を終わらせる
13.00000
guest00@nitfcei:~$ echo $? # プロセスの実行結果の値を参照するためのシェル変数 $?
0
guest00@nitfcei:~$ ./a.out
^D # データを入力せずにすぐに終了させる。
No data
guest00@nitfcei:~$ echo $?
1
シェルスクリプト
今まで、コマンドラインで命令の入力をしてきたが、こういったキーボードと対話的処理を行うプログラムは shell (シェル) と呼ばれ、今回の演習では、/bin/bash を用いている。 shell は、キーボードとの対話的処理だけでなく、shell で入力するような処理をファイルに記録しておき、そのファイルに記載されている順に処理を実行することができる。
guest00@nitfcei:~$ cp /home0/Challenge/3-shellscript/helloworld.sh . guest00@nitfcei:~$ cat helloworld.sh #!/bin/bash echo "Hello World" message="こんにちは" # シェル変数への代入 echo "Hello World = $message" # シェル変数の参照 guest00@nitfcei:~$ bash helloworld.sh # bash で helloworld.sh を実行する Hello World Hello World = こんにちは
シェルスクリプトの基本は、キー入力で実行するようなコマンドを書き並べればいい。
しかし、プログラムを実行する度に、bash ファイル名 と入力するのは面倒。こういう時には以下の2つの設定を行う。
- シェルスクリプトの先頭行に 実行させる shell の名前の前に “#!” をつける。
この行は、通称”シバン shebang (シェバン)“と呼ばれ、bashで実行させたいのなら”#!/bin/bash“、プログラミング言語 Perl で実行させたいのなら “#!/usr/bin/perl” とか、Python で実行させたいのなら、”#!/usr/bin/python” のようにすればいい。(今回のサンプルはすでに記入済み) - 保存したスクリプトに対して、実行権限を与える。
“ls -al “で “rw-r–r–” のようなファイルの書き込みパーミッションが表示されるが、通常ファイルの場合は、“x”の表示があると、プログラムとして実行可能となる。(フォルダであれば、rwxr-xr-x のように”x”の表示があると、フォルダの中に入ることができる)
((( 実効権限の設定 ))) guest00@nitfcei:~$ chmod 755 helloworld.sh guest00@nitfcei:~$ ./helloworld.sh Hello World Hello World = こんにちは
$HOME/.bashrc
シェルスクリプトは、Linux の環境設定を行うためのプログラム言語として使われている。
例えば、ユーザがログインする際には、そのユーザがどういった言語を使うのか(LC_LANG,LANG)や、どういったプログラムをよく使うのか(PATH,LD_LIBRARY_PATH)などは、そのユーザの好みの設定を行いたい。こういう時に、shell に bash を使っているのであれば、$HOME/.bashrc に、shell を使う際の自分好みの設定を記載すればいい。
((( $HOME/.bashrc の例 )))
#!/bin/bash
# PATHの設定
export PATH=/usr/local/bin:/usr/bin:/bin
# MacOS でインストールされているソフトで PATH を切り替える
if [ -d /opt/homebrew/bin ]; then # /opt/homebrew/bin のディレクトリがあるならば...
# HomeBrew
export PATH=/opt/homebrew/bin:$PATH
elif [ -d /opt/local/bin ]; then # /opt/local/bin のディレクトリがあるならば...
# MacPorts
export PATH="/opt/local/bin:$PATH"
fi
ユーザ固有の設定以外にも、OSが起動する時に、起動しておくべきプログラムの初期化作業などにもシェルスクリプトが使われている。
例えば、/etc/init.d/ フォルダには、Webサーバ(apache2)やsshサーバ(ssh) といったサーバを起動や停止をするための処理が、シェルスクリプトで記載してあり、OS 起動時に必要に応じてこれらのシェルスクリプトを使ってサーバソフトを起動する。(ただし最近は systemd が使われるようになってきた)