表計算ソフトの使い方(絶対参照・相対参照)
今日の表計算ソフトを使った演習では、下記のサンプルファイルを練習に使うので、Teamsで参照してください。
前回課題の答え合わせ
前回のレポートでは、sin(83度)(例)といった数値の有効数字を考えるというものを考えてもらったので、この有効数字をどう記載すべきか考えてみる。
課題を示す Excel ファイルでは、75度~89度あたりの角度で出題をするようにしてあった。注意しないといけない点は、sinは90度に近づくほど、1に近づく。このため、0.99…といった数値が求まるが、角度がちょっと変化しても、0.99といった部分はほぼ変化しない。だから、83が有効数字2桁ということで、0.99 といった有効数字2桁の書き方では、ちょっと不十分かもしれない。
そこで、83度(有効数字2桁)が小数点以下を丸められた数値と仮定する。この場合、元の数値は 82.5度~83.5度 の可能性がある。これらの値のsinを計算すると、0.9914から0.9935の間であり、小数点以下3桁目は、1~3 の値であり、結果を 0.992 (有効数字3桁) と記載しても良いかもしれない。
sin(82.5°) = 0.991444861 sin(83.0°) = 0.992546152 sin(83.5°) = 0.993571856
表計算ソフトの使い方
情報制御基礎では、プログラムで計算する所を、Excel のような表計算ソフトを用いて検証してもらったりする予定なので、Excel で計算式を使う方法を説明する。
セルの場所と簡単な式
簡単な、品名・単価・個数・価格の表を考える。以下の表のように、列の名前と、品名・単価・個数まで入力した後、単価と個数をかけた価格を求めるとする。
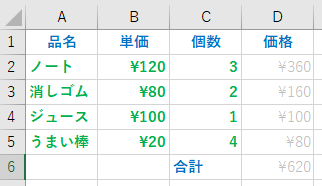
Excel では、表の列には左から、A,B,C,D… , 表の行には上から1,2,3,4,5 と番号が振られていて、特定の列・特定の行のデータを表す時には、列行を組み合わせ、A1に品名、B3に¥80、C5に4 が入っている。
例えば、D2 に、ノート単価120円、ノート個数3個をかけた値を入れたい場合は、D2の場所に、
=B2*C2
を書き込めば、その場所には360が表示される。
先頭の”=”を入力した後、該当する”B2″の場所をクリックするなりカーソルを操作すると、カーソルのセルの場所”B2″が自動的に入力される。さらに”*”を入力した後、”C2″の場所をクリックすれば”C2″が入力される。
Excelでは、入力する文字列の先頭が”=”の場合は、残り部分は計算式として扱われる。
D3には、”=B3*C3″を入力すれば、160 が表示される。しかし、この様な式を何度も入力するのは面倒である。
この場合、セル・カーソルを、D2 に合わせ、[右ボタン]-[コピー]を行い、D3 で[右ボタン]-[貼り付けオプション]-[貼り付け]を行えば、”=B3*C3″が入力される。
ここで注意しないといけないのが、式を張り付ける場合には、貼り付け先のセルの場所が一つ下の行なので、行番号を表す2の部分が1つ下の行番号3に書き換えられて、貼り付けが行われる。(相対参照)
関数式
例えば、下左図のような、数字とその平方根の表を作る場合、A2 に 1、B2に =sqrt( A2 ) を入力、A3 に =A2+1 を入力したあと、B2の式をB3にコピー&ペーストし、A3,B3 を A4~A6にペーストすればいい。
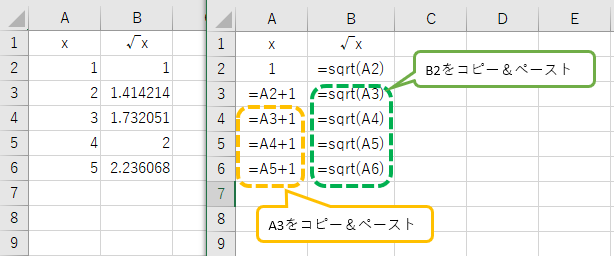
B2に入力したような、sqrt( A2 ) のようなものは、関数式と呼ばれる。
また、A3,B3 といった複数の行・列をまとめた範囲を示す時は、A3:B3 といった表記方法であらわす。
絶対参照と相対参照
最初の例に戻って、単価と個数の積で今度は税率を加えて計算する例を考える。また、税率は後で変化するかもしれないので、B1 のセルに税率を記入しておく場合を考える。
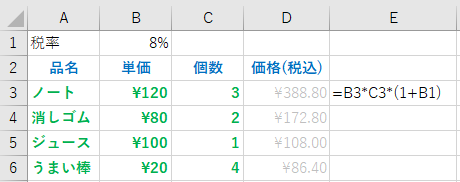
この場合、D3 には、” =B3*C3*(1+B1) ” を入力すればいい。
ただ、このように式を入力すると、D3 の計算式を、D4,D5,D6 にコピーすると、セル D4 には =B4*C4*(1+B2) が入力されてしまい、B2 には単価という文字が記載されているため、正しい結果が求まらない。
こういった場合には、絶対参照を用いる。D3 に記入する式を
=B3*C3*(1+$B$2)
とし、この D3 の式を D4 にコピー&ペーストすると、列記号、行番号の前に$がついた部分の式は、貼り付け場所に応じて変化しない。
このような、$B$2 といったセルの参照は、絶対参照と呼ぶ。これに対し、B2 といったセル参照は、貼り付け場所に応じて書き換えられるので、相対参照と呼ぶ。
絶対参照と相対参照が混ざった、$B2, B$2 といった書き方もある。
式の入力時に[F4ボタン]を押す度に、B2→$B$2→B$2→$B2→B2 と変化する$B2 は、式をコピーすると列部分はBのまま、行部分は場所に合わせて変化する。
B$2 は、式をコピーすると列部分は場所に合わせて変化し、行部分は2のままとなる。
レポート課題(第5回)
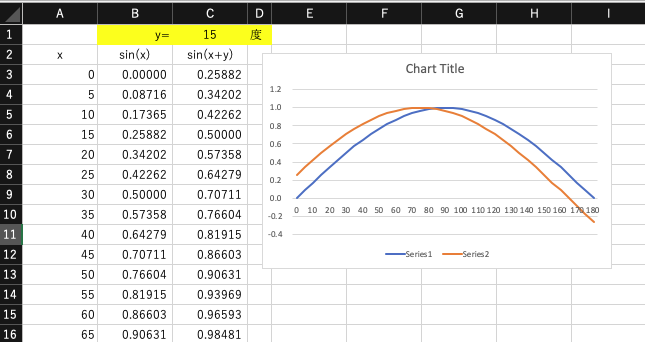
Excel で、xを0〜180度まで変化させたときのsin(x),位相をyとした時のsin(x+y)の値の表を作り、グラフ機能で表示せよ。A列は角度・B列はsin(x)・C列はsin(x+y)の値とし、yの値は”C1″に保存されているものとする。
この時、計算式の入力をどのように行なったのか(相対参照や絶対参照をどのように使ったのか)説明を、グラフの下に入力欄を設け記入せよ。
なお、Excel の sin() 関数は、引数がラジアンで入力する必要があるので、計算式には注意せよ。
そして出来上がった Excel のファイルを、Teams のこちらのフォルダに提出せよ。
プロセス管理とシェルスクリプト
ジョブ管理
プログラムを実行している時、それがすごくメモリも使い計算時間もかかる処理の場合、条件を変化させながら結果が欲しい時、どのように実行すべきだろうか?1つの処理が1時間かかるとして、画面を見ながら1時間後に処理が終わったことを確認してプログラムを実行するのか?
簡単な方法としては、1つ目の処理(仮にプログラムAとする)を実行させたままで、新しくウィンドウを開いてそこで新しい条件でプログラムを並行処理すればいい(プログラムBとする)と考えるかもしれない。しかし、メモリを大量に使用する処理をいくつも並行処理させると、仮想メモリが使われるようになる。結果的にスワッピングが発生する分、プログラムAを実行させた後にプログラムBを実行するための時間以上に、時間がかかることになる。
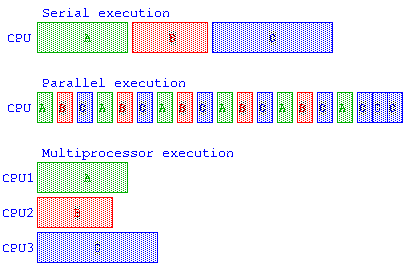
例えば、A,B,C のプロセスがあった場合、直列実行、並列実行、マルチプロセッサで並列実行のイメージ。時分割多重処理(Time Division Multiplexing – TDM) による並列実行では、各プロセスに割り当てられるCPUの最小実行単位時間をタイムクアンタム(Time Quantum)と呼ぶ。しかし、この処理のタスク切り替え(Task Switch)にかかる時間も考慮する必要がある。
ここで、プログラムを並行処理させるか、逐次処理させるといった、JOB(ジョブ)管理について説明を行う。
以下の説明で、複雑で時間のかかる処理を実行するとサーバの負担が高くなるので指定時間の処理待ちを行うための sleep 命令を使う。
逐次実行と並行実行
プログラムを連続して実行(処理Aの後に処理Bを実行する)場合には、セミコロン”;” で区切って A ; B のように処理を起動する。
guest00@nitfcei:~$ echo A A guest00@nitfcei:~$ echo A ; echo B A B
プログラムを並行して実行(処理Aと処理Bを並行処理)する場合には、アンド”&”で区切って A & B のように処理を起動する。
guest00@nitfcei:~$ sleep 5 & [1] 55 guest00@nitfcei:~$ echo A A [1]+ 終了 sleep 5 guest00@nitfcei:~$ sleep 2 & sleep 3 [1] 56 [1]+ 終了 sleep 2 guest00@nitfcei:~$ time ( sleep 1 ; sleep 1 ) # time コマンドは、コマンドの実行時間を測ってくれる。 real 0m2.007s user 0m0.005s sys 0m0.002s guest00@nitfcei:~$ time ( sleep 1 & sleep 1 ) real 0m1.002s user 0m0.003s sys 0m0.000s
fg, bg, jobs コマンド
プログラムを実行中に、処理(ジョブ)を一時停止したり、一時停止している処理を復帰させたりするときには、fg, bg, jobs コマンドを使う。
- 処理をしている時に、Ctrl-C を入力すると前面処理のプログラムは強制停止となる。
- 処理をしている時に、Ctrl-Z を入力すると前面処理のプログラムは一時停止状態になる。
- fg (フォアグラウンド) は、指定した処理を前面処理(キー入力を受け付ける処理)に変更する。
- bg (バックグラウンド) は、指定した処理を後面処理(キー入力が必要になったら待たされる処理)に変更する。
- jobs (ジョブ一覧) は、実行中や一時停止している処理(ジョブ)の一覧を表示する。
guest00@nitfcei:~$ sleep 10 # 途中で Ctrl-Z を入力する ^Z [1]+ 停止 sleep 10 guest00@nitfcei:~$ fg sleep 10 # 一時停止していた sleep 10 を実行再開 guest00@nitfcei:~$ sleep 3 ^Z [1]+ 停止 sleep 3 guest00@nitfcei:~$ sleep 4 ^Z [2]+ 停止 sleep 4 guest00@nitfcei:~$ jobs [1]- 停止 sleep 3 # [1],[2]というのはjob番号 [2]+ 停止 sleep 4 guest00@nitfcei:~$ fg %1 # ジョブ番号1 を前面処理にする sleep 3 guest00@nitfcei:~$ fg %2 # ジョブ番号2 を前面処理にする sleep 4
ps, kill コマンド
OS では、プログラムの処理単位は プロセス(process) と呼ぶ。OS はプロセスごとにメモリの実行範囲などの管理を行う。一連のプロセスを組み合わせて実行する単位を ジョブ(job) と呼ぶ。
複数のプロセスは間違ったメモリアクセスで他のプロセスが誤動作するようでは、安心して処理が実行できない。そこで、OS は、プロセスが他のプロセスのメモリをアクセスすると強制停止させるなどの保護をしてくれる。しかし、プロセスと他のプロセスが協調して処理を行うための情報交換のためにメモリを使うことは困難である。プロセス間で情報交換が必要であれば、パイプ機能やプロセス間共有メモリ機能を使う必要がある。
最近のOSでは、共通のメモリ空間で動き 並行動作する個々の処理は スレッド(thread) と呼び、その複数のスレッドをまとめたものがプロセスとなる。OS では、プロセスごとに番号が割り振られ、その番号を プロセスID(PID) と呼ぶ。実行中のプロセスを表示するには、ps コマンドを使う。
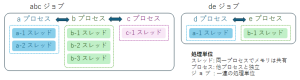
実行中のプロセスを停止する場合には、kill コマンドを用いる。停止するプログラムは、ジョブ番号(%1など) か プロセスID を指定する。
guest00@nitfcei:~$ sleep 3 ^Z [1]+ 停止 sleep 3 guest00@nitfcei:~$ sleep 4 ^Z [2]+ 停止 sleep 4 guest00@nitfcei:~$ jobs [1]- 停止 sleep 3 # [1],[2]というのはjob番号 [2]+ 停止 sleep 4 guest00@nitfcei:~$ ps w # プロセスの一覧(wを付けるとコマンドの引数も確認できる) PID TTY STAT TIME CMD 13 pts/0 Ss 00:00:00 -bash 84 pts/0 T 00:00:00 sleep 3 85 pts/0 T 00:00:00 sleep 4 86 pts/0 R 00:00:00 ps w guest00@nitfcei:~$ kill %1 [1]- Terminated sleep 3 guest00@nitfcei:~$ kill -KILL 85 [2]+ 強制終了 sleep 4 guest00@nitfcei:~$ ps ax # 他人を含めた全プロセスの一覧表示 PID TTY STAT TIME COMMAND 1 ? Ss 0:52 /sbin/init 2 ? S 0:00 [kthreadd] 3 ? I< 0:00 [rcu_gp] :
ここまでの授業では、OSでのリダイレクト・パイプの概念とプロセスの概念について説明を行ってきた。これによりプログラムの実行結果を他のプログラムに渡すことができる。これらの機能を使うと、いくつかのプログラムを次々と実行させるなどの自動化をしたくなってくる。そこで、これ以降では、OSとプログラムの間の情報を伝え合う基本機能の説明や、プログラムの起動をスクリプトとしてプログラム化するためのシェルスクリプト(shell script)について説明する。
環境変数
OSを利用していると、その利用者に応じた設定などを行いたい場合が多い。このような情報を管理する場合には、環境変数が使われる。環境変数はプロセス毎に管理され、プロセスが新しく子供のプロセス(子プロセス)を生成すると、環境変数は子プロセスに自動的に引き渡される。代表的な環境変数を以下に示す。
- HOME – ユーザがログインした際の起点となるディレクトリであり、/home/ユーザ名 となっているのが一般的。
シェルの中では”~” で代用できる。( “cd ~” で、最初のディレクトリに戻る ) - LC_ALL, LANG – ユーザが使う言語。OSからのメッセージなどを日本語で表示したい場合には、ja_JP.UTF-8 などを指定。
- TZ – ユーザの時差の情報(Time Zone) 日本であれば、”JST-9″ を設定するのが一般的。
日本標準時 “JST” で、グリニッジ標準時(GMT)との時差を表す “-9” の組み合わせ。 - PATH – ユーザがよく使うコマンドの保存されているディレクトリの一覧。/bin:/usr/bin の様にディレクトリ名を”:”区切りで書き並べる。
- LD_LIBRARY_PATH – 共有ライブラリの保存されているディレクトリの一覧。
環境変数と同じように、シェルの中で使われるものはシェル変数と呼ぶ。この変数は、子プロセスに引き渡されない。
環境変数を表示するには、env コマンド(環境変数を表示)や、set コマンド(環境変数やシェル変数を表示)を用いる。シェルの中で特定の環境変数を参照する場合には、$変数名 とする。echo コマンドで PATH を表示するなら、”echo $PATH” とすればいい。
guest00@nitfcei:~$ env SHELL=/bin/bash : guest00@nitfcei:~$ echo $PATH /bin:/usr/bin:/usr/local/bin
変数に値を設定する場合には、“変数名=値” の様に設定する。この変数を環境変数に反映させるには、export コマンドを用いるか、“export 変数名=値” を用いる。
環境変数の中で PATH は、コマンドを実行する際にコマンドの保存先を探すための変数であり、例えば PATH=/bin:/usr/bin:/usr/local/bin であったばあい、shell は、最初に /bin の中からコマンドを探し、次に /usr/bin を探し、さらに /usr/local/bin の中からコマンドを探す。PATH の設定の注意点
((( 環境変数の設定 ))) guest00@nitfcei:~$ PATH=/bin:/usr/bin guest00@nitfcei:~$ echo $PATH guest00@nitfcei:~$ export PATH guest00@nitfcei:~$ export PATH=/bin:/usr/bin:/usr/local/bin ((( PATHの確認 ))) guest00@nitfcei:~$ which zsh # which はコマンドの場所を探してくれる /bin/zsh guest00@nitfcei:~$ export PATH=/usr/local/bin:/usr/bin:/bin guest00@nitfcei:~$ which zsh /usr/bin/zsh ((( LC_ALL,LANG の確認 ))) guest00@nitfcei:~$ export LC_ALL=C guest00@nitfcei:~$ man man (英語でマニュアルが表示される) guest00@nitfcei:~$ export LC_ALL=ja_JP.UTF-8 guest00@nitfcei:~$ man man (日本語でマニュアルが表示される) ((( TZタイムゾーンの確認 ))) guest00@nitfcei:~$ export TZ=GMT-0 guest00@nitfcei:~$ date 2022年 7月 4日 月曜日 05:23:23 GMT # イギリスの時間(GMT=グリニッジ標準時間)が表示された guest00@nitfcei:~$ export TZ=JST-9 guest00@nitfcei:~$ date # 日本時間(JST=日本標準時間)で表示された 2022年 7月 4日 月曜日 14:23:32 JST guest00@nitfcei:~$ TZ=GMT-0 date ; date # 環境変数を一時的に変更して date を実行 2022年 7月 4日 月曜日 05:23:23 GMT 2022年 7月 4日 月曜日 14:23:32 JST
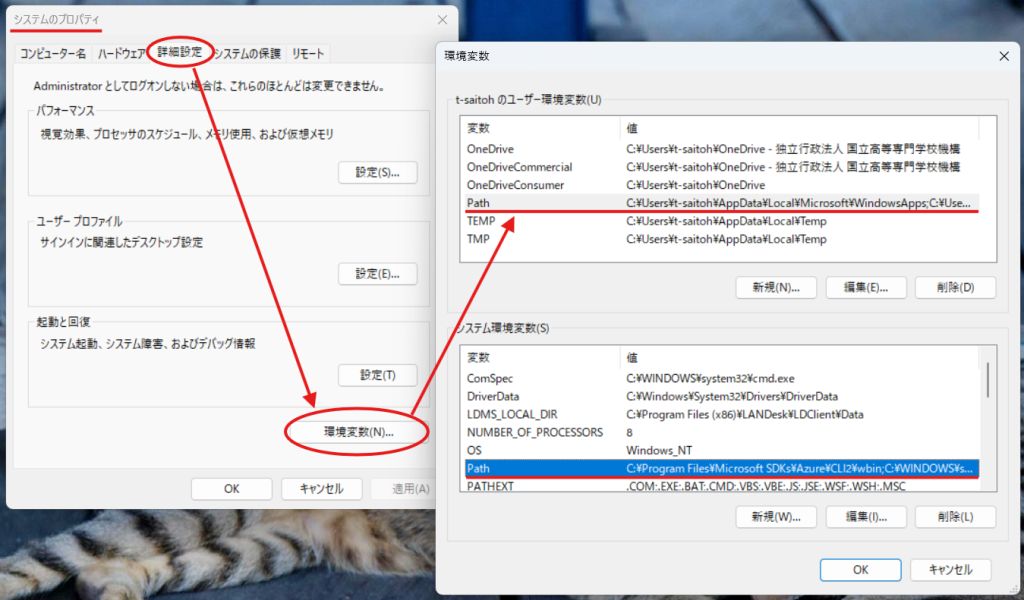
環境変数 PATH の考え方は、Windows でも同じように存在し、PATH を変更する場合には、「設定 – システムのプロパティ – 詳細設定 – 環境変数」により編集可能となる。
プログラムとコマンドライン引数と環境変数
この後に説明するシェルスクリプトなどの機能を用いる場合は、自分のプログラムとのデータのやり取りにコマンドライン引数と環境変数を使う。また、プログラムの実行に失敗した時に別の処理を実行するためには、main関数の返り値を使うことができる。
コマンドライン引数
コマンドライン引数は、プログラムを起動する時の引数として書かれている情報であり、C言語でこの情報を用いる時には、main関数の引数”int main( int argc , char** argv ) …” により値をもらうことができ、以下のようなプログラムを記述することで受け取ることができる。
# 参考として Java の場合のコマンドライン引数の取得方法も示す。
((( argv.c )))
#include <stdio.h>
int main( int argc , char** argv ) {
for( int i = 0 ; i < argc ; i++ ) {
printf( "argv[%d] = %s\n" , i , argv[ i ] ) ;
}
return 0 ;
}
((( argv.c を実行してみる )))
guest00@nitfcei:~$ cp /home0/Challenge/3-shellscript/argv.c .
guest00@nitfcei:~$ gcc argv.c
guest00@nitfcei:~$ ./a.out 111 aaa 234 bcdef
argv[0] = ./a.out
argv[1] = 111
argv[2] = aaa
argv[3] = 234
argv[4] = bcdef
((( Argv.java )))
import java.util.* ;
public class Argv {
public static void main( String[] args ) throws Exception {
for( int i = 0 ; i < args.length ; i++ )
System.out.println( "args["+i+"] = "+args[i] ) ;
}
}
((( Argv.java を実行してみる )))
guest00@nitfcei:~$ cp /home0/Challenge/3-shellscript/Argv.java .
guest00@nitfcei:~$ javac Argv.java
guest00@nitfcei:~$ java Argv 111 aaa 234 bcdef
args[0] = 111 # Java では コマンド名argv[0]は引数に含まれない
args[1] = aaa
args[2] = 234
args[3] = bcdef
注意点:コマンドライン引数の0番目には、プロセスを起動した時のプロセス名が入る。
環境変数の参照
C言語のmain関数は、コマンドライン引数のほかに環境変数も参照することができる。envpの情報は、getenv関数でも参照できる。
((( argvenvp.c )))
#include <stdio.h>
int main( int argc , char** argv , char** envp ) {
// コマンドライン引数argc,argvの処理
for( int i = 0 ; i < argc ; i++ ) {
printf( "argv[%d] = %s\n" , i , argv[ i ] ) ;
}
// 環境変数envpの処理
for( int i = 0 ; envp[i] != NULL ; i++ ) {
printf( "envp[%d] = %s\n" , i , envp[ i ] ) ;
}
return 0 ;
}
((( argvenvp.c を実行してみる )))
guest00@nitfcei:~$ cp /home0/Challenge/3-shellscript/argvenvp.c .
guest00@nitfcei:~$ gcc argvenvp.c
guest00@nitfcei:~$ ./a.out
argv[0] = ./a.out
envp[0] = SHELL=/bin/bash
:
プロセスの返す値
プログラムによっては、処理が上手くいかなかったことを検知して、別の処理を実行したいかもしれない。
こういう場合には、C言語であれば main の返り値に 0 以外の値で return させる。( exit関数を使ってもいい )
以下の例では、入力値の平均を出力するが、データ件数が0件であれば平均値を出力できない。こういう時に、”return 1 ;” のように値を返せば、シェル変数 $? (直前のコマンドの返り値) に return で返された値を参照できる。
((( average.c )))
#include <stdio.h>
int main() {
int count = 0 ;
int sum = 0 ;
char buff[ 1024 ] ;
while( fgets( buff , sizeof( buff ) , stdin ) != NULL ) {
int value ;
if ( sscanf( buff , "%d" , &value ) == 1 ) {
sum += value ;
count++ ;
}
}
if ( count == 0 ) {
// データ件数が0の場合は平均が計算できない。
fprintf( stderr , "No data\n" ) ;
// プログラムが失敗したことを返すには 0 以外の値を return する。
return 1 ; // exit( 1 ) ;
} else {
printf( "%lf\n" , (double)sum / (double)count ) ;
}
return 0 ;
}
((( average.c を動かしてみる )))
guest00@nitfcei:~$ gcc average.c
guest00@nitfcei:~$ ./a.out
12
14
^D # Ctrl-D で入力を終わらせる
13.00000
guest00@nitfcei:~$ echo $? # プロセスの実行結果の値を参照するためのシェル変数 $?
0
guest00@nitfcei:~$ ./a.out
^D # データを入力せずにすぐに終了させる。
No data
guest00@nitfcei:~$ echo $?
1
シェルスクリプト
今まで、コマンドラインで命令の入力をしてきたが、こういったキーボードと対話的処理を行うプログラムは shell (シェル) と呼ばれ、今回の演習では、/bin/bash を用いている。 shell は、キーボードとの対話的処理だけでなく、shell で入力するような処理をファイルに記録しておき、そのファイルに記載されている順に処理を実行することができる。
guest00@nitfcei:~$ cp /home0/Challenge/3-shellscript/helloworld.sh . guest00@nitfcei:~$ cat helloworld.sh #!/bin/bash echo "Hello World" message="こんにちは" # シェル変数への代入 echo "Hello World = $message" # シェル変数の参照 guest00@nitfcei:~$ bash helloworld.sh # bash で helloworld.sh を実行する Hello World Hello World = こんにちは
シェルスクリプトの基本は、キー入力で実行するようなコマンドを書き並べればいい。
しかし、プログラムを実行する度に、bash ファイル名 と入力するのは面倒。こういう時には以下の2つの設定を行う。
- シェルスクリプトの先頭行に 実行させる shell の名前の前に “#!” をつける。
この行は、通称”シバン shebang (シェバン)“と呼ばれ、bashで実行させたいのなら”#!/bin/bash“、プログラミング言語 Perl で実行させたいのなら “#!/usr/bin/perl” とか、Python で実行させたいのなら、”#!/usr/bin/python” のようにすればいい。(今回のサンプルはすでに記入済み) - 保存したスクリプトに対して、実行権限を与える。
“ls -al “で “rw-r–r–” のようなファイルの書き込みパーミッションが表示されるが、通常ファイルの場合は、“x”の表示があると、プログラムとして実行可能となる。(フォルダであれば、rwxr-xr-x のように”x”の表示があると、フォルダの中に入ることができる)
((( 実効権限の設定 ))) guest00@nitfcei:~$ chmod 755 helloworld.sh guest00@nitfcei:~$ ./helloworld.sh Hello World Hello World = こんにちは
$HOME/.bashrc
シェルスクリプトは、Linux の環境設定を行うためのプログラム言語として使われている。
例えば、ユーザがログインする際には、そのユーザがどういった言語を使うのか(LC_LANG,LANG)や、どういったプログラムをよく使うのか(PATH,LD_LIBRARY_PATH)などは、そのユーザの好みの設定を行いたい。こういう時に、shell に bash を使っているのであれば、$HOME/.bashrc に、shell を使う際の自分好みの設定を記載すればいい。
((( $HOME/.bashrc の例 )))
#!/bin/bash
# PATHの設定
export PATH=/usr/local/bin:/usr/bin:/bin
# MacOS でインストールされているソフトで PATH を切り替える
if [ -d /opt/homebrew/bin ]; then # /opt/homebrew/bin のディレクトリがあるならば...
# HomeBrew
export PATH=/opt/homebrew/bin:$PATH
elif [ -d /opt/local/bin ]; then # /opt/local/bin のディレクトリがあるならば...
# MacPorts
export PATH="/opt/local/bin:$PATH"
fi
ユーザ固有の設定以外にも、OSが起動する時に、起動しておくべきプログラムの初期化作業などにもシェルスクリプトが使われている。
例えば、/etc/init.d/ フォルダには、Webサーバ(apache2)やsshサーバ(ssh) といったサーバを起動や停止をするための処理が、シェルスクリプトで記載してあり、OS 起動時に必要に応じてこれらのシェルスクリプトを使ってサーバソフトを起動する。(ただし最近は systemd が使われるようになってきた)
理解度確認
UMLと振る舞い図
前回の講義で説明した構造図に続いて、処理の流れを説明するための振る舞い図の説明。
講義の後半は、UML作成のレポートの課題時間とする。
振る舞い図
参考資料をもとに振る舞い図の説明を行う。
ユースケース図
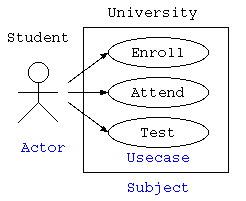
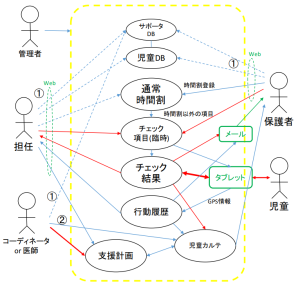
ユーザなど外部からの要求に対する、システムの振る舞いを表現するための活用事例や機能を表す図がユースケース図。 システムを構築する際に、最初に記述するUMLであり、システムに対する処理要件の全体像や機能を理解するために記述する。 ユーザや外部のシステムは、アクターとよび人形の絵で示す。楕円でシステムに対する具体的な処理をユースケースとして楕円で記述する。 関連する複数のユースケースをまとめて、サブジェクトとして示す場合もある。
上記の例は、学生が受講登録をして、授業に参加し、テストを受けるという様を表現したユースケース図である。また、下記の例にて、私自身が児童の保護システムを構築した際のユースケース図を示す。このように、システムの機能がどういったものがあるのかを網羅的に説明する際にユースケース図がよく使われる。
アクティビティ図
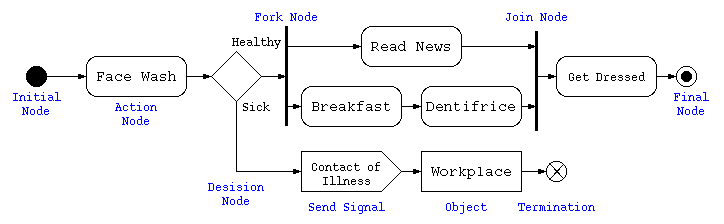
処理順序を記述するための図にはフローチャートがあるが、上から下に処理順序を記述するため、縦長の図になりやすい。また、四角枠の中に複雑なことを書けないので、UMLではアクティビティ図を用いる。
上記のアクティビティ図は、朝起きて出勤するまでの処理の流れを記述したものである。フローチャートと違い上から下に延びる図に限らず左右に広げて記載してある。
初期状態●から、終了状態◉までの手順を示すためのものがアクティビティ図。 フローチャートに無い表現として、複数の処理を並行処理する場合には、フォークノードで複数の処理を併記し、最終的に1つの処理になる部分をジョインノードで示す。 通常の処理は、角丸の長方形で示し、条件分岐(デシジョンノード)や合流(マージノード)はひし形で示す。
ステートチャート図(状態遷移図)
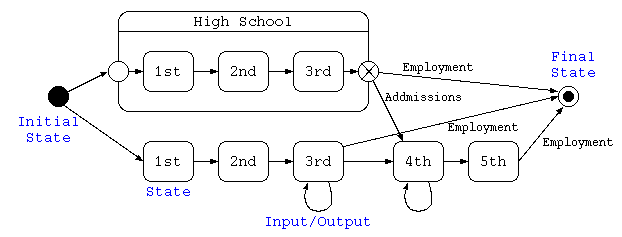
ステートチャート図は、処理内部での状態遷移を示すための図。 1つの状態を長丸長方形で示し、初期状態●から終了状態◉までを結ぶ。 1つの状態から、なんらかの状態で他の状態に遷移する場合は、分岐条件となる契機(タイミング)とその条件、およびその効果(出力)を「契機[条件]/効果」で矢印に併記する。 複数の状態をグループ化して表す場合もある。
上記のステートチャート図は、普通高校と高専の入学から卒業就職までを記載したものである。
シーケンス図
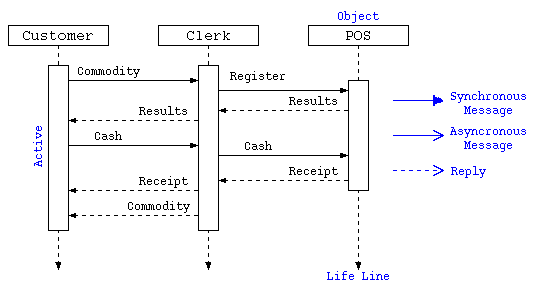
複数のオブジェクトが相互にやり取りをしながら処理が進むようなもののタイミングを記述するためのものがシーケンス図という。 上部の長方形にクラス/オブジェクトを示し、その下に縦軸にて時系列の処理の流れの線(Life Line)を描く。 オブジェクトがアクティブな状態は、縦長の長方形で示し、そのLife Line間を、やり取り(メッセージ)の線で相互に結ぶ。 メッセージは、相手側からの返答を待つような同期メッセージは、黒塗り三角矢印で示す。 返答を待たない非同期メッセージは矢印で示し、返答は破線で示す。
上のシーケンス図は、顧客が店員と対応しながらPOS端末でお金の出し入れをする様を表現したものとなっている。
コミュニケーション図
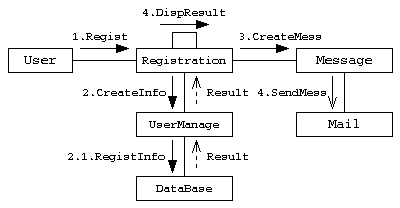
クラスやオブジェクトの間の処理とその応答(相互作用)と関連の両方を表現する図。
応答を待つ同期メッセージは -▶︎、非同期メッセージは→で表す。複数のオブジェクト間のやりとりの相互作用を表現する。
タイミング図
タイミング図は、クラスやオブジェクトの時間と共に状態がどのように遷移するのかを表現する図。
状態変化の発生するタイミングや、時間的な遅れや時間的な制約を図で明記するために使われる。
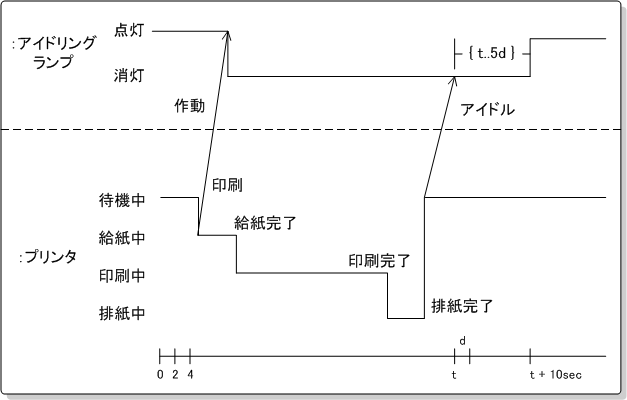
IT専科・UML入門より引用
UMLで人に説明する図の書き方として紹介してきたけど、よく現場で使われる図としては、ポンチ絵も名前だけは紹介したい。
ポンチ絵
ポンチ絵は、元々は風刺画のような漫画のことをであったが、最近ではビジネススの世界では「構想図」の意味で使われる。 製図の下書きとして作成するものや、イラストや図を使って概要をまとめた企画書などのことを言う。UMLのような書式のルールがある訳ではなく、相手に如何に印象付けるかが基本であり、ポンチ絵1つで企画の是非がきまったりもする。
- かっこいいポンチ絵の描き方 (アーキテクチャ図)
# プレゼンで文字密度の高いポンチ絵で説明されると、時として細かい所が読めずにイライラすることもある。
製図の下書きとしてのポンチ絵

イラストや図で概要をまとめた企画書としてのポンチ絵
実数の取り扱いと誤差
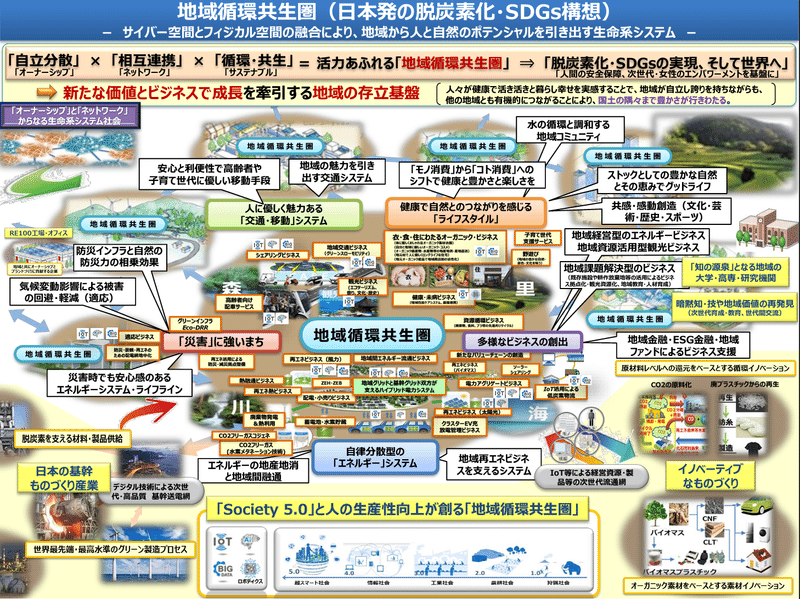
実数型(float / double)
実数型は、単精度実数(float型)と、倍精度実数(double型)があり、それぞれ32bit,64bitでデータを扱う。
指数表現は、大きい値や小さい値を表現する場合に使われ、物理などで1.2345×10-4といった、仮数×基数指数で表現する方法。数学や物理では基数に10を用いるが、コンピュータの世界では基数を2とすることが多い。
単精度型(float)では、符号1bit,指数部8bit,仮数部23bitで値を覚え、数値としては、以下の値を意味する。
符号✕ 1.仮数部 ✕ 2(指数数部-127)
符号部は、正の値なら0, 負の値なら1 を用いる。
仮数部が23bitなので、有効桁(正しい桁の幅)は10進数で約7桁となる。(1.2345678 と 1.2345679 は区別できない)
例えば、float型で扱える最大数は、以下のようになる。
0,1111,1110,111,1111,1111,1111,1111,1111 = 1.1111…×2127 ≒ 2128 ≒ 1038
指数部が1111,1111は、桁あふれで無限大になった値を表す特殊な数字として扱われるので、値として有効な指数部は1111,1110 となっている。
float 型は、計算精度が低いので 通常の数値計算のプログラミングではあまり使われることはない。一方で、ゲームなどの3次元座標計算などでは、精度は必要もないことから、GPU(グラフィックス専用のプロセッサ)では float 型を使うことも多い。また、最近の機械学習のプログラミングでは、神経の動きをまねた計算(ニューラルネットワークプログラミング)が行われるが、これも精度はあまり高くなくてもいいので float 型を使うことも多く、グラフィックス用の GPU で float 型で機械学習の計算を行うことも多い。
倍精度型(double)では、符号1bit,指数部11bit,仮数部52bitで値を覚え、数値としては、以下の意味を持つ。
符号✕ 1.仮数部 ✕ 2(指数部-1023)

これらの実数で計算を行うときには、0.00000001011×210といった値の時に、仮数部に0が並んだ状態を覚えると、計算の精度が低くなるので、1.01100000000×22のように指数部の値を調整して小数点の位置を補正しながら行われる。
double型の場合、52bit=10進数16桁相当の有効桁、最大数で、1.1111…×21023≒10308
倍精度型を使えば、正しく計算できるようになるかもしれないが、実数型はただの加算でも仮数部の小数点の位置を合わせたりする処理が必要で、浮動小数点専用の計算機能を持っていないような、ワンチップコンピュータでは整数型にくらべると10倍以上遅い場合もある。
実数の注意点
C言語でプログラムを作成していて、簡単な数値計算のプログラムでも動かないと悩んだことはないだろうか?解らなくて友達のプログラムを真似したら動いたけど、なぜ自分のプログラムは動かなかったのか深く考えたことはあるだろうか?
単純な合計と平均
整数を入力し、最後に合計と平均を出力するプログラムを以下に示す。
しかし、C言語でこのプログラムを動かすと、10,10,20,-1 と入力すると、合計(sum)40,件数(cnt)3で、平均は13と表示され、13.33333 とはならない。
小数点以下も正しく表示するには、どうすればいいだろうか?
ただし、変数の型宣言を “double data,sum,cnt ;” に変更しないものとする。
// 入力値の合計と平均を求める。
#include <stdio.h>
int main() {
int data ;
int sum = 0 ;
int cnt = 0 ;
for(;;) {
printf( "数字を入力せよ。-1で終了¥n" ) ;
scanf( "%d" , &data ) ;
if ( data < 0 )
break ;
cnt = cnt + 1 ;
sum = sum + data ;
}
printf( "合計 %d¥n" , sum ) ;
printf( "平均 %d¥n" , sum / cnt ) ;
}
C言語では、int型のsum / int型のcnt の計算は、int 型で計算を行う(小数点以下は切り捨てられる)。このため、割り算だけ実数で行いたい場合は、以下のように書かないといけない。
printf( "平均 %lf¥n" , (double)sum / (double)cnt ) ;
// (double)式 は、sum を一時的に実数型にするための型キャスト
まずは動く例
以下のプログラムは、見れば判るけど、th を 0度〜360度まで5度刻みで変化させながら、y = sin(th) の値を表示するプログラム。
// sin の値を出力
#include <stdio.h>
#include <math.h>
int main() {
double th , y ;
for( th = 0.0 ; th <= 360.0 ; th += 5.0 ) {
y = sin( th / 180.0 * 3.1415926535 ) ;
printf( "%lf %lf¥n" , th , y ) ;
}
return 0 ;
}
動かないプログラム
では、以下のプログラムはどうだろうか?
// case-1 ---- プログラムが止まらない
#define PI 3.1415926535
int main() {
double th , y ;
// 0〜πまで100分割でsinを求める
for( th = 0.0 ; th != PI ; th += PI / 100.0 ) {
y = sin( th ) ;
printf( "%lf %lf¥n" , th , y ) ;
}
return 0 ;
}
// case-2 ---- y の値が全てゼロ
int main() {
int th ;
double y ;
for( th = 0 ; th <= 360 ; th += 5 ) {
y = sin( th / 180 * 3.1415926535 ) ;
printf( "%d %lf¥n" , th , y ) ;
}
return 0 ;
}
どちらも、何気なく読んでいると、動かない理由が判らないと思う。そして、元のプログラムと見比べながら、case-1 では、「!=」を「<=」に書き換えたり、case-2 では、「int th ;」を「double th ;」に書き換えたら動き出す。
では何が悪かったのか…
回答編
数値と誤差
コンピュータで計算すると、計算結果はすべて正しいと勘違いをしている人も多い。ここで、改めて誤差について考える。特に、計器で測定した値であれば、測定値自体に誤差が含まれている。
こういった誤差が含まれる数字を扱う場合注意が必要である。例えば実験値を手書きで記録する場合、12.3 と 12.300 では意味が異なる。測定値であやふやな桁を丸めたのであれば、前者は 12.2500〜12.3499… の間の値であり有効数字3桁である。後者は、12.2995〜12.300499… の間の値であり、有効数字5桁である。このため、誤差が含まれる数字の加算・減算・乗算・除算では注意が必要である。
加減乗除算の場合
加減算であれば小数点の位置を揃え、誤差が含まれる桁は有効桁に含めてはいけない。

上記の計算では、0.4567の0.0567の部分は意味がないデータとなる。(情報落ち)
乗除算であれば、有効桁の少ない値と有効桁の多い値の計算では、有効桁の少ない方の誤差の影響が計算結果に出てくるため、通常は、有効桁5桁と2桁の計算であれば、乗除算結果は少ない2桁で書くべきである。

桁落ち
有効桁が大きい結果でも、減算が含まれる場合は注意が必要である。
例えば、以下のような計算では、有効桁7桁どうしでも、計算結果の有効桁は3桁となる。

このような現象は、桁落ちと呼ばれる。
演習問題(4回目)
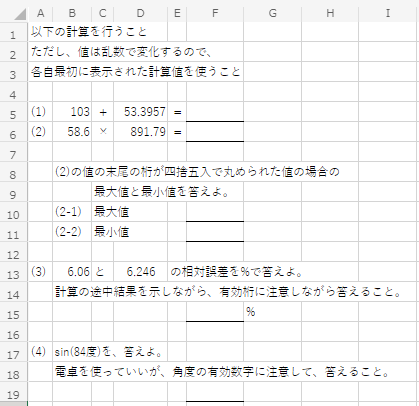
こちらのフォルダに示す、Excel の表で、有効桁を考えてもらうための演習問題(ランダムに値が作られます)を有効数字を考えながら計算し、答えをレポートにまとめてください。例を以下に示す。
レポートは、こちらのひな型をベースに作成し(手書きノートをキャプチャした資料でもOKです)、同じフォルダに提出してください。
LOG解析のおまけ
ログ解析のレポートを早々に提出してくれたものの中に、64.124.8.135 からのアクセスが沢山あった…との結果だけど、
$ grep 2025-06-24-access.log 64.124.8.135 | head -1 64.124.8.135 - - [24/Jun/2025:04:07:08 +0900] "GET /~t-saitoh/etc/2013/1301191410-1_640x480.jpg HTTP/1.1" 404 501 "-" "Mozilla/5.0 (compatible; ImagesiftBot; +imagesift.com)"
この結果を見ると、LOGの履歴の最後は、”Mozilla/5.0 (compatible; ImagesiftBot; +imagesift.com)” となっている。この欄は、ユーザエージェント欄で、相手がどんなブラウザでアクセスしているかなどが分かる欄。でも、注目すべきなのは、 ImagesiftBot という項目がある。これは、ブラウザではなくデータ検索ロボット(Bot)だと思われる。名前からして、画像に特化したロボットが、いくつかの画像ファイルをまとめて取っていったのだろう。
パイプとフィルタ
フィルタプログラム
パイプを使うと、標準入力からデータをもらい・標準出力に結果を出力するような簡単なプログラムを組み合わせて、様々な処理が簡単にできる。こういったプログラムは、フィルタと呼ぶ。
簡単な例として、入力をすべて大文字に変換するプログラム(toupper)、入力文字をすべて小文字に変換するプログラム(tolower)が、下記の例のように保存してあるので動作を確かめよ。
guest00@nitfcei:~$ cp /home0/Challenge/2.1-RedirectPipe.d/toupper.c .
guest00@nitfcei:~$ gcc -o toupper toupper.c .
guest00@nitfcei:~$ cat toupper.c | ./toupper
#INCLUDE <STDIO.H>
#INCLUDE <CTYPE.H>
INT MAIN() {
INT C ;
WHILE( (C = GETCHAR()) != EOF )
PUTCHAR( TOUPPER( C ) ) ;
RETURN 0 ;
}
guest00@nitfcei:~$ cp /home0/Challenge/2.1-RedirectPipe.d/tolower.c .
guest00@nitfcei:~$ gcc -o tolower tolower.c
guest00@nitfcei:~$ cat tolower.c | ./tolower
(((何が出力されるか答えよ)))
よく使われるフィルタのまとめ
| 文字パターンを含む行だけ出力 | grep 文字パターン |
| 文字パターンを含まない行を出力 文字パターンを正規表現でマッチングし該当行を出力 大文字小文字を区別しない |
grep -v 文字パターン grep -e 正規表現 grep -i 文字パターン |
| 入力文字数・単語数・行数をカウント(word counter) | wc |
| 入力行数をカウント | wc -l |
| データを昇順に並べる | sort |
| データを降順に並べる 先頭を数字と見なしてソート(-gなしの場合、文字とみなしてソート) |
sort -r sort -g |
| 同じ行データが連続したら1つにまとめる | uniq |
| 同じ行が連続したら1つにまとめ、連続した数を出力 | uniq -c |
| 空白区切りで指定した場所(1番目)を抽出 | awk ‘{print$1;}’ |
| 入力の先頭複数行を表示(10行) | head |
| 入力の末尾複数行を表示(10行) | tail |
| 指定した行数だけ、先頭/末尾を表示 | head -行数 tail -行数 |
| 入力したデータを1画面分表示した所で一時停止する(ページャ) more は、最も単純なページャで、SPACE で1画面送り、ENTER で1行送り、”q”で終了。 lv は前後に移動できるページャで、カーソルキー↑(b)↓(f) で行を前後に移動できる。 |
more lv |
LOG解析
Linux は利用者に様々なサービスを提供するサーバで広く利用されている。しかし、幅広いサービス提供となると、中にはウィルス拡散や個人情報収集のための悪意のあるアクセスも増えてくる。
このためサーバでは、アクセスを受けた時の状況を記録し保存する。このような情報はアクセス履歴、ログと呼ぶ。
ログの中には、以下のような情報が混在することになるが、大量の 1. や 2. 目的のアクセスの中に、3. や 4. といったアクセスが混ざることになるが、これを見逃すとシステムに不正侵入を受ける可能性もある。
- 本来の利用者からのアクセス
- 検索システムの情報収集(クローラーからのアクセス)
- 不正な情報収集のためのアクセス
- システムの不備を探して不正侵入などを試みるアクセス
今回の演習では、電子情報の web サーバのとある1日のアクセス履歴ファイルを用い、パイプ機能を使い様々なフィルタを使い LOG解析の練習を行う。
アクセス履歴の解析
Webサーバのアクセス履歴が、/home0/Challenge/2.2-LOG.d/access.log に置いてある。このファイルで簡単な確認をしてみよう。
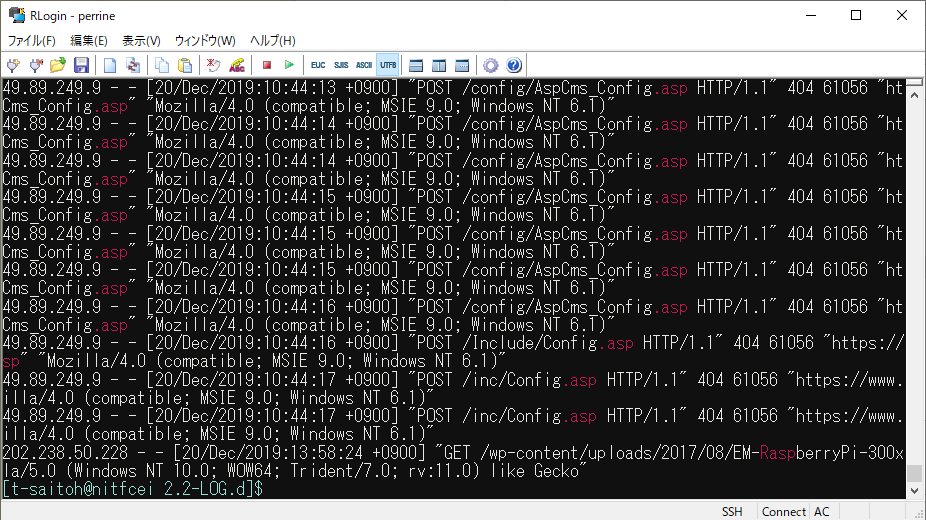
(( ファイルの場所に移動 )) $ cd /home0/Challenge/2.2-LOG.d/ (( .asp という文字を含む行を表示 )) $ grep .asp access.log
電子情報のWebサーバには、.asp (WindowsのWebサーバで動かすプログラムの拡張子) など存在しない。明らかに設定不備を探すための攻撃である。
これを見ると、grep で .asp を含む行が抜粋され、.asp の部分が強調されていることで、攻撃を簡単に確認できる。しかしこれは画面行数で10件程度が確認できるが、本当は何回攻撃を受けたのだろうか?この場合は、行数をカウントする”wc -l” を使えばいい。
(( アクセス回数を数える )) $ grep .asp access.log | wc -l 37
access.log の各項目の意味
電子情報のWebサーバの access.log に記録されている各項目の意味は以下の通り。
| 項目 | log項目 | 内容 |
|---|---|---|
| 1 | %h | リモートホスト。WebサーバにアクセスしてきたクライアントのIPアドレス |
| 2 | %l | リモートログ名。説明略。通常は “-“ |
| 3 | %u | ログインして操作するページでのユーザ名。通常は “-“ |
| 4 | %t | アクセスを受けた時刻 |
| 5 | %r | 読み込むページ。アクセス方法(GET/POSTなど)と、アクセスした場所。 |
| 6 | %>s | ステータスコード。(200成功,403閲覧禁止,404Not Found) |
| 7 | %b | 通信したデータのバイト数。 |
| 8 | %{Referer}i | Referer どのページからアクセスが発生したのか |
| 9 | %{User-Agent}i | User-Agent ブラウザ種別(どういったブラウザからアクセスされたのか) |
以下に、フィルタプログラムを活用して、色々な情報を探す例を示す。実際にコマンドを打って何が表示されるか確認しながら、フィルタプログラムの意味を調べながら、何をしているか考えよう。
.asp を使った攻撃を探す
(( .asp を試す最初の履歴を探す )) $ grep "\.asp" access.log | head -1 49.89.249.9 - - [20/Dec/2019:09:19:06 +0900] "POST /Include/md5.asp HTTP/1.1" 404 64344 "https://www.ei.fukui-nct.ac.jp/Include/md5.asp" "Mozilla/4.0 (compatible; MSIE 9.0; Windows NT 6.1)" (( 49.89.249.9 がどんなアクセスを試みているのか探す )) $ grep ^49.89.249.9 access.log | head 49.89.249.9 - - [20/Dec/2019:09:19:06 +0900] "POST /Include/md5.asp HTTP/1.1" 404 64344 "https://www.ei.fukui-nct.ac.jp/Include/md5.asp" "Mozilla/4.0 (compatible; MSIE 9.0; Windows NT 6.1)" 49.89.249.9 - - [20/Dec/2019:09:19:06 +0900] "POST /inc/md5.asp HTTP/1.1" 404 61056 "https://www.ei.fukui-nct.ac.jp/inc/md5.asp" "Mozilla/4.0 (compatible; MSIE 9.0; Windows NT 6.1)"せ
- 正規表現とは
- \.asp と先頭に \ がついているのは、ピリオドだけだと「ワイルドカード文字の任意の1文字の意味」になるため、ワイルドカードをエスケープしている。
- ^49.89…. の先頭に ^ がついているのは、行頭にマッチングさせるため。
- ステータスコードが404は”Not Found”なので、読み出しに失敗している。
- IPアドレス検索で、49.89.249.9 がどこのコンピュータか調べよう。
攻撃の時間を確認
(( 49.89.249.9 がどんな時間にアクセスを試みているのか探す ))
$ grep ^49.89.249.9 access.log | awk '{print $4;}'
[20/Dec/2019:09:19:06
[20/Dec/2019:09:19:06
[20/Dec/2019:09:19:07
:
- 不正アクセスを試みている時間を調べると、そのアクセス元の09:00~17:00に攻撃していることがわかる場合がある。どういうこと?
ページの閲覧頻度を確認
(( /~t-saitoh/ 見たIPアドレスと頻度 ))
$ grep "/~t-saitoh/" access.log | awk '{print $1;}' | sort | uniq -c | sort -g -r | head
38 151.80.39.78
35 151.80.39.209
32 203.104.143.206
31 5.196.87.138
:
- grep – “/~t-saitoh/”のページをアクセスしているデータを抽出
- awk – 項目の先頭(IPアドレス)だけ抽出
- sort – IPアドレス順に並べる(同じIPアドレスならその数だけ重複した行になる)
- uniq – 重複している行数を数える
- sort -g -r – 先頭の重複数で大きい順にソート
- head – 先頭10行だけ抽出
(( /~t-saitoh/ 見たIPアドレスと頻度 )) (( t-saitoh のテスト問題のページを誰が見ているのか? )) $ grep "/~t-saitoh/exam/" access.log 5.196.87.156 - - [20/Dec/2019:06:36:02 +0900] "GET /~t-saitoh/exam/db2009/ex2009-5-1.pdf HTTP/1.1" 200 20152 "-" "Mozilla/5.0 (compatible; AhrefsBot/6.1; +http://ahrefs.com/robot/)" : (( クローラーのアクセスが多くてよくわからないので bot を含まない行を抽出 )) $ grep "/~t-saitoh/exam/" access.log | grep -v -i bot | lv 213.242.6.61 - - [20/Dec/2019:06:33:12 +0900] "GET /%7Et-saitoh/exam/ HTTP/1.0" 200 19117 "http://www.ei.fukui-nct.ac.jp/%7Et-saitoh/exam/" "Mozilla/5.0 (Windows NT 6.1; WOW64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/67.0.3396.87 Safari/537.36 OPR/54.0.2952.64 (Edition Yx)" 188.163.109.153 - - [20/Dec/2019:06:43:04 +0900] "GET /%7Et-saitoh/exam/ HTTP/1.0" 200 19117 "http://www.ei.fukui-nct.ac.jp/%7Et-saitoh/exam/" "Mozilla/5.0 (Windows NT 6.1; WOW64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/66.0.3359.170 Safari/537.36 OPR/53.0.2907.99" 188.163.109.153 - - [20/Dec/2019:06:43:05 +0900] "POST /cgi-bin/movabletype/mt-comments.cgi HTTP/1.0" 404 432 "http://www.ei.fukui-nct.ac.jp/%7Et-saitoh/exam/" "Mozilla/5.0 (Windows NT 6.1; WOW64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/66.0.3359.170 Safari/537.36 OPR/53.0.2907.99" 45.32.193.50 - - [20/Dec/2019:07:06:15 +0900] "GET /~t-saitoh/exam/apply-prog.html HTTP/1.0" 200 5317 "http://www.ei.fukui-nct.ac.jp/" "Mozilla/5.0 (Windows NT 5.2) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/63.0.3239.132 Safari/537.36"
- この結果を見ると mt-comments.cgi というアクセスが見つかる。どうも コメントスパム(ブログのコメント欄に広告を勝手に書き込む迷惑行為)をしようとしている。
ネットワーク攻撃への対処
今回の access.log のアクセス履歴解析は、Webサーバへのアクセスへの基本的な対処となる。しかし、もっと違うネットワーク接続ではどのような対処を行うべきであろうか?
一般的には、
- サーバにネットワークアクセスの記録ソフトを使う(例ネットワークプロトコルアナライザーWireShark)
- ファイアウォールのアクセス履歴を解析
授業内レポート
- ここまでのLOG解析の例の1つについて、どういう考え方でフィルタを使っているのか、自分の言葉で説明せよ。
- LOG 解析のためのコマンドを考え、その実行結果を示し、それから何が判るか説明せよ。
(例) 自分で考えたコマンドの実行結果をつけたうえで、「コメントスパムを何度も試す危ないアクセス元は〇〇である。」 - レポート提出先フォルダ ファイル名は、出席番号2桁-名前-レポート名.docx (ファイル形式は pdf などでも良い) とする。
UMLと構造図
UMLの構造図の書き方の説明。 詳しくは、参考ページのUML入門などが、分かりやすい。
クラス図
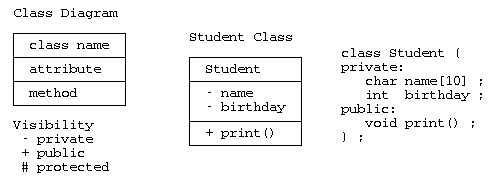
クラス図は、構造図の中の基本的な図で、 枠の中に、上段:クラス名、中段:属性(要素)、下段:メソッド(関数)を記載する。 属性やメソッドの可視性を示す場合は、”-“:private、”+”:public、”#”:protected 可視性に応じて、”+-#”などを記載する。
関連
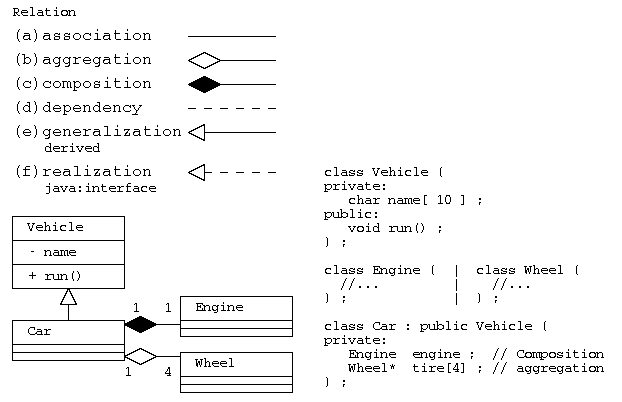
クラスが他のクラスと関係がある場合には、その関係の意味に応じて、直線や矢印で結ぶ。
(a)関連(association):単純に関係がある場合、
(b)集約(aggregation):部品として持つが、弱い結びつき。関係先が消滅しても別に存在可能。(has-a)
(c)コンポジション(composition):部品として持つが強い結びつき。関係先と一緒に消滅。(has-a)
(d)依存(dependency):依存関係にあるだけ
(e)派生(generalization):派生・継承した関係(is-a)
(f)実現(realization): Javaでのinterfaceによる多重継承
上図の例では、乗り物クラスVehicleから自動車Carが派生し(CarからVehicleへの三角矢印―▷)、 自動車は、エンジン(Engine)を部品として持つ(EngineからCarへのひし形矢印―◆)。エンジンは車体と一緒に廃棄なら、コンポジション(C++であれば部品の実体を持つ)で実装する。
自動車は、同じく車輪(Wheel)を4つ持つが、自動車を廃棄してもタイヤは別に使うかもしれないので、集約(部品への参照を持つ)で実装する(WheelからCarへのひし形矢印―◇)。 集約で実装する場合は、C++などであれば、ポインタで部品を持ち、部品の廃棄(delete)は、別に行うことになる。
Javaなどのプログラム言語では、オブジェクトはデータの実体へのポインタで扱われるため、コンポジションと集約を区別して表現することは少ない。
is-a 、has-a の関係
前の課題でのカモノハシクラスで、羽や足の情報をどう扱うべきかで、悩んだ場合と同じように、 クラスの設計を行う場合には、部品として持つのか、継承として機能を持つのか悩む場合がある。 この場合には、“is-a”の関係、“has-a”の関係で考えると、部品なのか継承なのか判断しやすい。
たとえば、上の乗り物(Vehicle)クラスと、車(Car)のクラスは、”Car is-a Vehicle” といえるので、is-a の関係。 “Car is-a Engine”と表現すると、おかしいことが判る。 車(Car)とエンジン(Engine)のクラスは、”Car has-a Engine”といえるので、has-a の関係となる。 このことから、CarはVehicleからの派生であり、Carの属性としてEngineを部品として持つ設計となる。
ER図
UMLではないが、オブジェクト図に近いものとしてER図がある。これはリレーショナルデータベースの設計が正しいか確認しながら設計するための図で、Entity(実体)とRelation(関連)を相互に線で結んだもので、最近のER図の書き方は、かなりクラス図の書き方に似ている。
オブジェクト図
クラス図だけで表現すると、複雑なクラス関係では、イメージが分かりづらい場合がでてくる。 この場合、具体的な値を図に書き込んだオブジェクトで表現すると、説明がしやすい場合がある。 このように具体的な値で記述するクラス図は、オブジェクト図と言う。 書き方としては、クラス名の下に下線を引き、中段の属性の所には具体的な値を書き込んで示す。
その他の構造図
パッケージ図
パッケージ図は、クラス図をパッケージ毎に分類して記載する図。 パッケージのグループを、フォルダのような図で記載する。

IT専科から引用
コンポーネント図とコンポジット構造図
コンポジット構造図は、クラスやコンポーネントの内部構造を示すもので、コンポーネント図は、複数のクラスで構成される処理に、 インタフェースを用意し、あたかも1つのクラスのように扱ったもの。 接続するインタフェースを飴玉と飴玉を受けるクチのイメージで、提供側を◯───で表し、要求側を⊃──で表す。
IT専科から引用
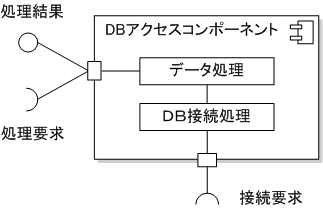
配置図
配置図は、システムのハードウェア構成や通信経路などを表現するための図。 ハードウェアは直方体の絵で表現し、 デバイスの説明は、”≪device≫”などを示し、実行環境には、”≪executionEnvironment≫” などの目印で表現する。
IT専科から引用
スタックと待ち行列
前回の授業では、リストの先頭にデータを挿入する処理と、末尾に追加する処理について説明したが、この応用について説明する。
計算処理中に一時的なデータの保存として、スタック(stack)と待ち行列・キュー(queue)がよく利用される。それを配列を使って記述したり、任意の大きさにできるリストを用いて記述することを示す。
スタック
配列を用いたスタック
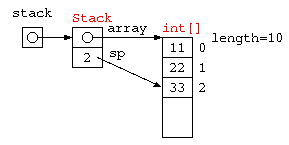
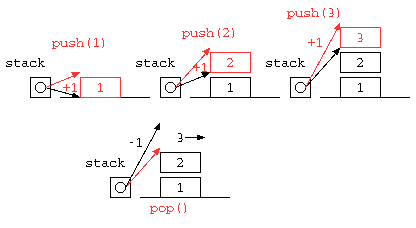
一時的な値の記憶によく利用されるスタック(stack)は、データの覚え方の特徴からLIFO( Last In First out )とも呼ばれる。配列を使って記述すると以下のようになるであろう。
import java.util.*;
public class Main {
static final int STACK_SIZE = 10 ;
static int[] stack = new int[ STACK_SIZE ] ;
static int sp = 0 ;
static void push( int x ) {
stack[ sp++ ] = x ;
}
static int pop() {
return stack[ --sp ] ;
}
public static void main(String[] args) throws Exception {
push( 11 ) ;
push( 22 ) ;
push( 33 ) ;
System.out.println( pop() ) ;
System.out.println( pop() ) ;
System.out.println( pop() ) ;
}
}
配列を使った Stack をオブジェクト指向で記述するなら、以下のように書ける。
import java.util.*;
class Stack {
static final int STACK_SIZE = 10 ;
int[] array ;
int sp ;
Stack() {
this.array = new int[ STACK_SIZE ] ;
this.sp = 0 ;
}
void push( int x ) {
array[ sp++ ] = x ;
}
int pop() {
return array[ --sp ] ;
}
} ;
public class Main {
public static void main(String[] args) throws Exception {
Stack stack = new Stack() ;
stack.push( 11 ) ;
stack.push( 22 ) ;
stack.push( 33 ) ;
System.out.println( stack.pop() ) ;
System.out.println( stack.pop() ) ;
System.out.println( stack.pop() ) ;
}
}
C言語で書いた場合
#define STACK_SIZE 32
int stack[ STACK_SIZE ] ;
int sp = 0 ;
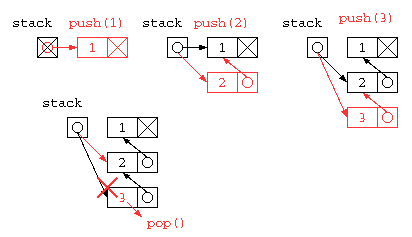
void push( int x ) { // データをスタックの一番上に積む
stack[ sp++ ] = x ;
}
int pop() { // スタックの一番うえのデータを取り出す
return stack[ --sp ] ;
}
void main() {
push( 1 ) ; push( 2 ) ; push( 3 ) ;
printf( "%d\n" , pop() ) ; // 3
printf( "%d\n" , pop() ) ; // 2
printf( "%d\n" , pop() ) ; // 1
}

++,–の前置型と後置型の違い
// 後置インクリメント演算子 int i = 100 ; printf( "%d" , i++ ) ; // これは、 printf( "%d" , i ) ; i++ ; // と同じ。100が表示された後、101になる。 // 前置インクリメント演算子 int i = 100 ; printf( "%d" , ++i ) ; // これは、 i++ ; printf( "%d" , i ) ; // と同じ。101になった後、101を表示。
リスト構造を用いたスタック
しかし、この中にSTACK_SIZE以上のデータは貯えられない。同じ処理をリストを使って記述すれば、配列サイズの上限を気にすることなく使うことができるだろう。では、リスト構造を使ってスタックの処理を記述してみる。
import java.util.*;
class ListNode {
int data ;
ListNode next ;
ListNode( int d , ListNode n ) {
this.data = d ;
this.next = n ;
}
}
public class Main {
static ListNode stack = null ;
static void push( int x ) {
stack = new ListNode( x , stack ) ;
}
static int pop() {
int ans = stack.data ;
stack = stack.next ;
return ans ;
}
public static void main(String[] args) throws Exception {
push( 1 ) ;
push( 2 ) ;
push( 3 ) ;
System.out.println( pop() ) ;
System.out.println( pop() ) ;
System.out.println( pop() ) ;
}
}
struct List* stack = NULL ;
void push( int x ) { // リスト先頭に挿入
stack = cons( x , stack ) ;
}
int pop() { // リスト先頭を取り出す
int ans = stack->data ;
struct List* d = stack ;
stack = stack->next ; // データ 0 件で pop() した場合のエラー対策は省略
free( d ) ;
return ans ;
}
オブジェクト指向っぽく書くならば、下記のようになるだろう。初期状態で stack = null にしておくと、stack.push() ができないので、stack の先頭には、ダミーデータを入れるようにプログラムを書くと以下のようになるだろう。
import java.util.*;
class ListNode {
int data ;
ListNode next ;
ListNode( int d , ListNode n ) {
this.data = d ;
this.next = n ;
}
ListNode() { // stack初期化用のコンストラクタ
this.data = -1 ;
this.next = null ;
}
void push( int x ) {
this.next = new ListNode( x , this.next ) ;
}
int pop() {
int ans = this.next.data ;
this.next = this.next.next ;
return ans ;
}
} ;
public class Main {
public static void main(String[] args) throws Exception {
ListNode stack = new ListNode() ; // stack初期化用のコンストラクタを使う
stack.push( 1 ) ;
stack.push( 2 ) ;
System.out.println( stack.pop() ) ;
System.out.println( stack.pop() ) ;
}
}
キュー(QUEUE)
2つの処理の間でデータを受け渡す際に、その間に入って一時的にデータを蓄えるためには、待ち行列(キュー:queue)がよく利用される。 データの覚え方の特徴からFIFO(First In First Out)とも呼ばれる。
配列を用いたQUEUE / リングバッファ
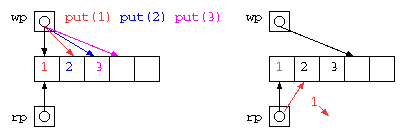
配列にデータを入れる場所(wp)と取り出す場所のポインタ(rp)を使って蓄えれば良いが、配列サイズを超えることができないので、データを取り出したあとの場所を循環して用いるリングバッファは以下のようなコードで示される。
import java.util.*;
public class Main {
static final int QUEUE_SIZE = 32 ;
static int[] queue = new int[ QUEUE_SIZE ] ;
static int wp = 0 ;
static int rp = 0 ;
static void put( int x ) {
queue[ wp++ ] = x ;
if ( wp >= QUEUE_SIZE ) // wp = wp % QUEUE_SIZE ; or wp = wp & (QUEUE_SIZE - 1) ;
wp = 0 ;
}
static int get() {
int ans = queue[ rp++ ] ;
if ( rp >= QUEUE_SIZE ) // rp = rp % QUEUE_SIZE ; or rp = rp & (QUEUE_SIZE - 1) ;
rp = 0 ;
return ans ;
}
public static void main(String[] args) throws Exception {
// Your code here!
put( 1 ) ;
put( 2 ) ;
put( 3 ) ;
System.out.println( get() ) ;
System.out.println( get() ) ;
System.out.println( get() ) ;
}
}
#define QUEUE_SIZE 32
int queue[ QUEUE_SIZE ] ;
int wp = 0 ; // write pointer(書き込み用)
int rp = 0 ; // read pointer(読み出し用)
void put( int x ) { // 書き込んで後ろ(次)に移動
queue[ wp++ ] = x ;
if ( wp >= QUEUE_SIZE ) // 末尾なら先頭に戻る
wp = 0 ;
}
int get() { // 読み出して後ろ(次)に移動
int ans = queue[ rp++ ] ;
if ( rp >= QUEUE_SIZE ) // 末尾なら先頭に戻る
rp = 0 ;
return ans ;
}
void main() {
put( 1 ) ; put( 2 ) ; put( 3 ) ;
printf( "%d\n" , get() ) ; // 1
printf( "%d\n" , get() ) ; // 2
printf( "%d\n" , get() ) ; // 3
}

このようなデータ構造も、get() の実行が滞るようであれば、wp が rp に循環して追いついてしまう。このため、上記コードはまだエラー対策としては不十分である。どのようにすべきか?
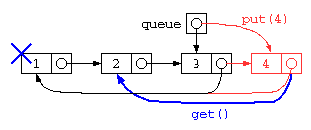
リスト構造を用いたQUEUE
前述のリングバッファもget()しないまま、配列上限を越えてput()を続けることはできない。
この配列サイズの上限問題を解決したいのであれば、リスト構造を使って解決することもできる。この場合のプログラムは、以下のようになるだろう。
import java.util.*;
class ListNode {
int data ;
ListNode next ;
ListNode( int d , ListNode n ) {
this.data = d ;
this.next = n ;
}
} ;
public class Main {
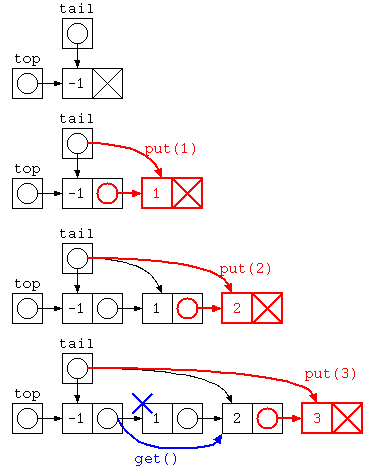
static ListNode top = new ListNode( -1 , null ) ;
static ListNode tail = top ;
static void put( int x ) {
tail.next = new ListNode( x , null ) ;
tail = tail.next ;
}
static int get() {
int ans = top.next.data ;
top.next = top.next.next ;
return ans ;
}
public static void main(String[] args) throws Exception {
put( 1 ) ;
put( 2 ) ;
put( 3 ) ;
System.out.println( get() ) ;
System.out.println( get() ) ;
System.out.println( get() ) ;
}
}
Javaで書かれた ListNode を用いた待ち行列のイメージ図は下記のように示される。
struct List* queue = NULL ;
struct List** tail = &queue ;
void put( int x ) { // リスト末尾に追加
*tail = cons( x , NULL ) ;
tail = &( (*tail)->next ) ;
}
int get() { // リスト先頭から取り出す
int ans = queue->data ;
struct List* d = queue ;
queue = queue->next ;
free( d ) ;
return ans ;
}
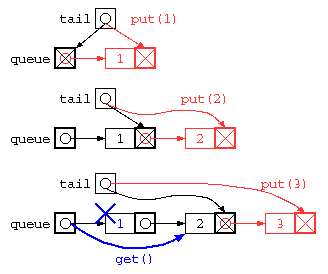
ただし、上記のプログラムは、データ格納後にget()で全データを取り出してしまうと、tail ポインタが正しい位置になっていないため、おかしな状態になってしまう。
また、このプログラムでは、rp,wp の2つのポインタで管理することになるが、 2重管理を防ぐために、リストの先頭と末尾を1つのセルで管理する循環リストが使われることが多い。
理解確認
- 配列を用いたスタック・待ち行列は、どのような処理か?図などを用いて説明せよ。
- リスト構造を用いたスタック・待ち行列について、図などを用いて説明せよ。
- スタックや待ち行列を、配列でなくリスト構造を用いることで、どういう利点があるか?欠点があるか説明せよ。
- 配列を用いたリングバッファが用いられている身近な例にはどのようなものがあるか?
- 配列を用いたリングバッファを実装する場合配列サイズには 2n 個を用いることが多いのはなぜだろうか?
リスト処理のレポート課題(前期期末)
プログラムは書いて・動かして・間違って・直す が重要ということで、以下に前期期末試験前までに取り組むレポート課題をしめす。
レポート課題(プログラム例)
Java を用いて、後に示すデータ処理をするためのリスト構造を定義し、与えられたデータを追加していく処理を作成せよ。
課題の説明用に、複素数のリスト構造を定義し、指定した絶対値以下の複素数を抜き出す関数をつくった例を示す。
import java.util.* ;
class ComplexListNode {
double re ;
double im ;
ComplexListNode next ;
ComplexListNode( double r , double i , ComplexListNode n ) {
this.re = r ;
this.im = i ;
this.next = n ;
}
} ;
public class Main {
// 先頭からデータを挿入する方式
static ComplexListNode top = null ;
// 全リストを表示する処理
static void print( ComplexListNode p ) {
for( ; p != null ; p = p.next ) {
System.out.println( "(" + p.re + ")+j(" + p.im + ")" ) ;
}
}
// top に要素を追加する処理(先頭に入れる)
static void add( double r , double i ) {
top = new ComplexListNode( r , i , top ) ;
}
// 特定のデータを対象にした処理の例
static ComplexListNode filter_lessthan( ComplexListNode p , double v_abs ) {
ComplexListNode ans = null ;
for( ; p != null ; p = p.next ) {
if ( Math.sqrt( p.re * p.re + p.im * p.im ) <= v_abs )
ans = new ComplexListNode( p.re , p.im , ans ) ;
}
return ans ;
}
public static void main(String[] args) throws Exception {
add( 1.0 , 2.0 ) ;
add( -1.0 , -1.0 ) ;
add( 2.0 , -1.0 ) ;
add( 1.0 , 0 ) ;
print( top ) ;
ComplexListNode less_than_2 = filter_lessthan( top , 2 ) ;
System.out.println( "less than 2" ) ;
print( less_than_2 ) ;
}
}
((( 実行結果の例 )))
(1.0)+j(0.0)
(2.0)+j(-1.0)
(-1.0)+j(-1.0)
(1.0)+j(2.0)
less than 2
(-1.0)+j(-1.0)
(1.0)+j(0.0)
レポート内容
上記のプログラムをまねて、以下のレポート課題を作成すること。テーマは ((出席番号-1)%3+1) を選択すること。
- 年号のデータが、年号の名称と年号の始まりの年月日がYYYYMMDD形式で
- “Meiji”,18681023
- “Taisho”,19120730
- “Showa”,19261225
- “Heisei”,19890108
- “Reiwa”,20190501
の様に与えられる。このデータ構造を覚えるリスト構造を作成せよ。また ListNode のデータで、西暦の日付のリストが seireki_list = new ListNode( 19650207, new ListNode( 20030903 , null ) ) ; のように与えられたら、そのデータを和暦で表示するプログラムを作成せよ。 (参考2023年前期期末)
- 市町村名,月,日,最高気温,最低気温のデータが、
- “fukui”,8月,4日,27.6℃,22.3℃
- “fukui”,8月,5日,31.5℃,23.3℃
- “fukui”,8月,7日,34.7℃,25.9℃
- “obama”,8月,6日,34.2℃,23.9℃
の様に与えられる。このデータ構造で覚えるリスト構造を作成せよ。また、この中から真夏日(最高気温が30℃以上)でかつ熱帯夜(最低気温が25℃以上)の日のリストを抽出し表示するプログラムを作成せよ。(参考2022年前期期末)
- ホスト名と、IPアドレス(0~255までの8bitの値✕4個で与えるものとする)のデータ構造で、
- “www.fukui-nct.ac.jp”,104,215,54,205
- “perrine.tsaitoh.net”,192,168,11,2
- “dns.fukui-nct.ac.jp”,10,10,21,51
- “dns.google.com”,8,8,8,8
の様に与えられる。このデータ構造をリスト構造で覚えるプログラムを作成せよ。また、この中からプライベートアドレスのリストを抽出し表示するプログラムを作成せよ。プライベートアドレスは 10.x.x.x, 172.16~31.x.x,192.168.x.x とする。(参考2019年前期期末)
プログラムを作るにあたり、リスト構造には add( 与えられたデータ… ) のように呼び出してリストに追加すること。この時、生成されるリストが、登録の逆順になるか(先頭に挿入)、登録順(末尾に追加)になるかは、自分の理解度に応じて選択すること。抽出する処理を書く場合も登録順序どおりにするかは自分の理解度に応じて選べばよい。
また、理解度に自信がある人は、add() などの処理を「オブジェクト指向」のように記述する方法を検討すること。
あくまで、リスト構造の理解を目的とするため、ArrayList<型> , LinkedList<型> のようなクラスは使わないこと。(ただし考察にて記述性の対比の対象として使うのはOK。複素数の場合の LinkedList を使った例を以下に示す。)
import java.util.* ;
import java.util.stream.Collectors ;
class Complex {
double re ;
double im ;
Complex( double r , double i ) {
this.re = r ;
this.im = i ;
}
public double abs() {
return Math.sqrt( re * re + im * im ) ;
}
@Override
public String toString() {
return "(" + re + ")+j(" + im + ")" ;
}
} ;
public class Main {
public static LinkedList<Complex> top = new LinkedList<Complex>() ;
// 絶対値が指定した値以下の要素だけを集める関数
public static LinkedList<Complex> filter_lessthan(
LinkedList<Complex> list , double v_abs ) {
var ans = new LinkedList() ;
for( var c : list ) {
if ( Math.sqrt( c.re * c.re + c.im * c.im ) <= v_abs )
ans.add( c ) ;
}
return ans ;
}
public static void main( String[] args ) throws Exception {
// リストに複素数を追加
top.add( new Complex( 1.0 , 2.0 ) ) ;
top.add( new Complex( -1.0 , -1.0 ) ) ;
top.add( new Complex( 2.0 , -1.0 ) ) ;
top.add( new Complex( 1.0 , 0 ) ) ;
for( var c : top ) {
System.out.println( c ) ;
}
System.out.println( "---" ) ;
// static な関数でフィルタリング
for( var c : filter_lessthan( top , 2.0 ) ) {
System.out.println( c ) ;
}
/* Stream API を使ってフィルタリング
for( var c : top.stream() // LinkedList を Stream に変換
.filter( c->c.abs() < 2.0 ) // filter条件をラムダ式で渡す
.collect( Collectors.toList() ) // Collectorsで結果を集める
) {
System.out.println( c ) ;
}
*/
}
}
- LinkedListを使ったプログラム例(Paiza.io)
syslog とは
syslog とは
- OSからトラブルなどの履歴を残すためにLOGファイルに残す機能。
- Linuxのsyslogでは、rsyslog などにより、1つのサーバに履歴をネットワーク経由でまとめることができる。
- トラブルなどの原因などの種別ごとにファシリティが定義されている。
- kernel, user, daemon, mail, ….
- ファシリティ毎に出力ファイルを指定することができる。
- /etc/(r)syslog.conf , /etc/(r)syslog.d
- /var/log/syslog, dmesg, user.log , auth.log, mail.log
- syslog に出力するには
- logger コマンド
- syslog(3) – ライブラリ関数
- printk – カーネル内でメッセージ出力
システムコールとは
- ユーザーモードからカーネルモードを呼び出す
- カーネルモード
- すべてのハードウェアに直接アクセスでき、メモリ管理、プロセス管理、ファイルシステム管理など、システムの基本的な機能を制御する特権を持っています。
- カーネルモードを呼び出す関数はシステムコールと呼ぶ
システム監視ツール
- モニタリング
- Nagios – システムやネットワークの異常を検知し、管理者にアラートを送信
- Zabbix , Munin – 詳細なデータ収集と可視化機能を提供。
- 不正侵入検知システム(IDS)
- ホスト型 IDS
- rkhunter – ルートキット、バックドア、およびローカルエクスプロイトの可能性をスキャンして検出する
- ホスト型 IDS
FIreWall 管理ソフト
- iptables – 低レベルだけど柔軟な設定が可能。設定が複雑。
- firewalld – ゾーンベースの管理や動的な設定変更を可能にした高機能なツール。GUI ツールが充実。
- ufw – 初心者向け。iptablesのラッパーで、より簡単にファイアウォールを管理。