ホーム » t-saitoh の投稿 (ページ 2)

作者アーカイブ: t-saitoh

2025年7月
日 月 火 水 木 金 土
 12345
6789101112
13141516171819
20212223242526
2728293031  

リンク集

検索・リンク

Google Office 365

リダイレクトとパイプ

2025年6月17日

Linux/unixを使う上で、キーボードでコマンドを入力しているが、こういうコマンドの管理を行うプログラムを shell と呼ぶ。shell には、色々なものがある(sh, csh, bash, zsh)が、広く使われている bash( born-again shell )について説明する。最初に、コマンドの入出力を組み合わせるために重要となるリダイレクトとパイプについて説明する。

標準入出力とリダイレクト

出力リダイレクト

C言語のプログラミングで、プログラムの実行結果をレポートに張り付ける時はどのように行っているだろうか？多くの人は、実行画面を PrintScreen でキャプチャした画像を張り付けているかもしれない。しかし、数十行にわたる結果であれば何度もキャプチャが必要となる。
そこで、今日の最初はリダイレクト機能について説明する。

“gcc ファイル.c” は、C言語のプログラムをコンパイルし、a.out という実行ファイルを生成する。”./a.out” にてプログラムを実行する。実行する命令に、“> ファイル名” と書くと、通常の出力画面(標準出力) をファイル名に記録してくれる。これを出力リダイレクトと呼ぶ。また、“>> ファイル名” と書くと、既存ファイルの後ろに追記してくれる。

guest00@nitfcei:~$ cat helloworld.c
#include <stdio.h>
int main() {
    printf( "Hello World\n" ) ;
    return 0 ;
}

guest00@nitfcei:~$ gcc helloworld.c
guest00@nitfcei:~$ ./a.out
Hello World

guest00@nitfcei:~$ ./a.out > helloworld.txt

guest00@nitfcei:~$ cat helloworld.txt
Hello World

guest00@nitfcei:~$ ./a.out >> helloworld.txt

guest00@nitfcei:~$ cat helloworld.txt 
Hello World
Hello World 

入力リダイレクト

次に、1行に名前と3教科の点数が書いてある複数行に渡るデータの各人の平均点を求めるプログラムを考える。

guest00@nitfcei:~$ cp /home0/Challenge/2.1-RedirectPipe.d/avg-each-low.c .
guest00@nitfcei:~$ cat avg-each-low.c
#include <stdio.h>
// ((input))           ((output))
// saitoh  43  54 82   saitoh 59.67
// tomoko  89 100 32   tomoko 73.67
// mitsuki 79  68 93   mitsuki 80.00
int main() {
   char name[ 100 ] ;
   int point[ 3 ] ;
   while( scanf( "%s%d%d%d" ,
                 name , &point[0] , &point[1] , &point[2] ) == 4 ) {
      double sum = 0.0 ;
      for( int i = 0 ; i < 3 ; i++ )
         sum += point[i] ;
      printf( "%s %6.2f\n" , name , sum / 3.0 ) ;
   }
   return 0 ;
}

guest00@nitfcei:~$ gcc avg-each-low.c
guest00@nitfcei:~$ ./a.out
saitoh 43  54 82    入力
saitoh 59.67        出力
tomoko 89 100 32    入力
tomoko 73.67        出力
^D             ← Ctrl-D を押すとファイル入力を終了

しかし、プログラムの書き方を間違えてプログラムを修正していると、動作確認のたびに何度も同じデータを入力するかもしれないが、面倒ではないだろうか？

プログラムを実行する時に、“< ファイル名” をつけると、通常はキーボードから入力する所を、ファイルからの入力に切り替えて実行することができる。このようなscanf()を使う時のようなプログラムの入力を標準入力といい、それをファイルに切り替えることを入力リダイレクトと呼ぶ。

guest00@nitfcei:~$ cp /home0/Challenge/2.1-RedirectPipe.d/name-point3.txt .

guest00@nitfcei:~$ cat name-point3.txt
saitoh  43  54 82
tomoko  89 100 32
mitsuki 79  68 93 

guest00@nitfcei:~$ ./a.out < name-point3.txt
saitoh  59.67
tomoko  73.67
mitsuki 80.00

この入力リダイレクトと出力リダイレクトを合わせて使うこともできる。

guest00@nitfcei:~$ ./a.out < name-point3.txt > name-avg.txt

guest00@nitfcei:~$ cat name-avg.txt
saitoh  59.67
tomoko  73.67
mitsuki 80.00

パイプ

先の名前と3教科のプログラムの結果から、全員の平均点をも計算したい場合、どのようなプログラムを作るだろうか？C言語だけの知識なら、各人の行のデータを計算するループの中に、全員の合計と人数を求めるプログラムを書いて、最後に平均点を出力するだろう。

一方で、複数人の名前と平均点のデータから平均点を求めるプログラムを書いて、前述のプログラムの実行結果を使う人もいるだろう。

以下の例では、“gcc -o avg-each-row avg-each-row.c” で、avg-each-row という実行ファイル、“gcc -o avg-all avg-all.c” で、avg-all という実行ファイルを生成し、avg-each-row で入力リダイレクト・出力リダイレクトを使って、name-avg.txt を作り、avg-all を入力リダイレクトで、最終結果を表示している。

guest00@nitfcei:~$ cp /home0/Challenge/2.1-RedirectPipe.d/avg-all.c .
guest00@nitfcei:~$ cat avg-all.c
#include <stdio.h>
// ((input))      ((output))
// saitoh  59.67  73.11
// tomoko  73.67
// mitsuki 80.00
int main() {
   char name[ 100 ] ;
   double point ;
   double sum = 0 ;
   int count = 0 ;
   while( scanf( "%s%lf" , name , &point ) == 2 ) {
      sum += point ;
      count++ ;
   }
   printf( "%6.2f\n" , sum / (double)count ) ;
   return 0 ;
}

guest00@nitfcei:~$ gcc -o avg-each-low avg-each-low.c
guest00@nitfcei:~$ gcc -o avg-all avg-all.c

guest00@nitfcei:~$ ./avg-each-low < name-point3.txt > name-avg.txt

guest00@nitfcei:~$ ./avg-all < name-avg.txt
71.11

しかし、いちいち入出力の結果を name-avg.txt を作るのは面倒である。であれば、以下の様なイメージで処理をすれば答えが求まる。

name-point3.txt→(avg-each-row)→name-avg.txt→(avg-all)→結果

これは、パイプ機能を使って以下の様に動かすことができる。

guest00@nitfcei:~$ ./avg-each-low < name-point3.txt | ./avg-all
71.11

guest00@nitfcei:~$ cat name-point3.txt | ./avg-each-low | ./avg-all
71.11

プログラムを実行する時に、“A | B” ように書くと、プログラムA の標準出力結果を、プログラムB の標準入力に接続させて、2つのプログラムを実行できる。このような機能を、パイプと呼ぶ。上記例の2つめ “cat… | ./avg-each-low | ./avg-all” では3つのプログラムをパイプでつないでいる。

リダイレクトのまとめ

 

入力リダイレクト(標準入力) 実行コマンド < 入力ファイル
出力リダイレクト(標準出力) 実行コマンド > 出力ファイル
　出力リダイレクト(標準出力の追記) 実行コマンド >> 出力ファイル
　標準エラー出力のリダイレクト 実行コマンド 2> 出力ファイル
パイプ
コマンドAの標準出力をコマンドBの標準入力に接続		 コマンドA | コマンドB

標準エラー出力,/dev/null, /dev/zero デバイス

パイプやリダイレクトを使っていると、出力をファイルに保存する場合、途中で異常を伝える目的で出力メッセージを出力するものが見逃すかもしれない。こういった際に、計算結果などを出力する標準出力(stdout)とは別に標準エラー出力(stderr)がある。ファイルを使う際には、デバイスを区別するためのデバイス番号(ファイルディスクリプタ)を使う。この際に、標準入力(stdin) = 0, 標準出力(stdout) = 1, 標準エラー出力(stderr) = 2 という番号を使うことになっている。

#include <stdio.h>
int main() {
   int x , y ;
   scanf( "%d%d" , &x , &y ) ;
   if ( y == 0 )
      fprintf( stderr , "zero divide\n" ) ;
   else
      printf( "%f\n" , (double)x / (double)y ) ;
}

Unix のシステムでは、特殊なデバイスとして、/dev/null, /dev/zero というのがある。

/dev/null は、入力リダイレクトに使うと ファイルサイズ 0 byte のデータが得られるし、出力リダイレクトに使うと 書き込んだデータは捨てられる。 /dev/zero は、入力リダイレクトに使うと、’\0′ のデータを延々と取り出すことができ、ファイルをゼロで埋めるなどの用途で使う。

/dev/null の使い方の例としては、例えば標準エラー出力が不要なときは、コマンドラインで以下のようにすれば、標準エラー出力(デバイス番号2番)の内容を捨てることができる。

$ command 2> /dev/null





C言語のコンパイルまとめ


 






C言語のコンパイル(実行ファイルはa.out)
gcc ソースファイル




　実行ファイル名を指定してコンパイル
gcc -o 実行ファイル ソースファイル






 


理解度確認





Windows における PRN デバイス, AUX デバイス


/dev/null といった特殊デバイスの一例として、昔の Windows では PRN デバイス、AUX デバイスというのがあった。


C:< command > PRN



昔の文字印刷しかできないプリンタが普通だったころは、PRN という特殊デバイスがあって、このデバイスにリダイレクトをすれば、出力をプリンタに出力することができた。同じように AUX というデバイスは、通信ポートにつながっていて ” command > AUX ” と入力すれば、通信先にデータを送ることができた。最近のプリンタや通信デバイスはもっと複雑になっているためにこういった機能は使えなくなっているが、このデバイス名の名残りで、Windows では PRN とか AUX という名前のファイルを作ることはできない。









	
UMLの概要

	

		2025年6月17日 	

	
巨大なプロジェクトでプログラムを作成する場合、設計の考え方を図で示すことは、直感的な理解となるため重要であり、このために UML がある。以下にその考え方と記述方法を説明していく。


プログラムの考え方の説明


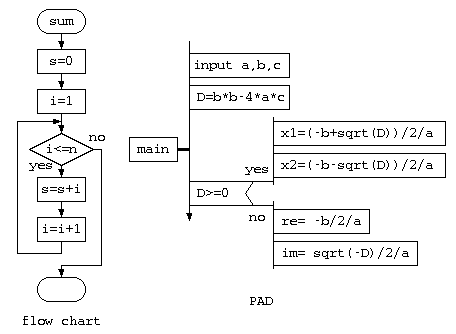
今まで、プログラムを人に説明する場合には、初心者向けの方式としてフローチャートを使うのが一般的であろう。しかし、フローチャートは四角の枠の中に説明を書ききれないことがあり、使い勝手が悪い。他には、PAD と呼ばれる記述法もある。この方法は、一連の処理を表す縦棒の横に、処理を表す旗を並べるようなイメージで記載する。




しかし、これらの記法は、手順を記載するためのものであり、オブジェクト指向ではデータ構造の理解も重要でありデータ構造を説明するための図が必要となってきた。


個人的な経験では、企業にてプログラムを作っていた頃(1990年頃)、UML などの考え方は普及していなかった。処理を説明するためのフローチャートでも、通信関係のプログラムでは、送信側と受信側の相互関係を説明する場合、フローチャートでは相互のタイミングなどの説明は困難であった。また、通信では、リトライ・タイムアウトといった状態も発生するが、その場合だと状態遷移図なども併記する必要があり、フローチャートの限界を感じていた。


また、データ構造については、オブジェクト指向も普及前であればデータ要素の一覧表が中心であった。プログラム書式(コーディングスタイル)などの統一もされていないので、同じチーム内で誤解などを解消するための意思統一が重要であった。


ドキュメントを残す技術


学生のみなさんは、プログラムの説明の文書はどのように残しているだろうか？


私が仕事をしていた頃は、プログラムと別にドキュメントをワープロで残そうとすると、プログラム変更に合わせて編集することが難しく、プログラムとドキュメントの乖離が発生する。このため、プログラムの中にコメントの形で残すことが重要であった。特にデータ構造の説明は、ヘッダファイルの中に大量のコメントで残すことが多かった。


企業であれば、関数宣言の前には、コーディングスタイルとして決められた書式のコメントで、引数や返り値などを明記することが求められるのが一般的。


文芸的プログラミング TeX


TeX(LaTeX)を改発した Knuth は、文芸的プログラミングとして、プログラム中にドキュメントを併記するための WEB(注記:Internetの意味のWebではない) を同時に開発している。このシステムでは、プログラムとドキュメントを併記したソースプログラムから、ドキュメントを取り出すプログラムと、ソースコードを取り出すプログラムがあり、情報の一体性を高めている。


手っ取り早くドキュメント Markdown


最近では、プログラムのエディタで Markdown という、マークアップ言語でドキュメントを残す場合も多いだろう。これであれば、プレーンテキストで書いたドキュメントを、HTMLやLaTeXといったWeb形式・論文形式といったドキュメントに変換も容易である。




このような方法で、ドキュメントとプログラムの乖離を防ぐことが重要となる。


github では、ドキュメントとして README.md といったファイル名で Markdown によるドキュメントを残すのが一般的。




UML記法が生まれるまで


巨大なプロジェクトでプログラムを作る場合、対象となるシステムを表現する場合、オブジェクト指向分析(Object Oriented Analysis)やオブジェクト指向設計(Object Oriented Design)とよばれるソフトウェア開発方法が重要となる。(総称して OOAD – Object Oriented Analysis and Design)


これらの開発方法をとる場合、(1)自分自身で考えを整理したり、(2)グループで設計を検討したり、(3)ユーザに仕様を説明したりといった作業が行われる。この時に、自分自身あるいはチームメンバーあるいはクライアントに直感的に図を用いて説明する。この時の図の書き方を標準化したものが UML であり、(a)処理の流れを説明するための振る舞い図(フローチャートやPAD)と、(b)データ構造を説明するための構造図を用いる。


UMLは、ランボーによるOMT(Object Modeling Technique どちらかというとOOA(Object Oriented Anarisys)中心)と、 ヤコブソンによるオブジェクト指向ソフトウェア工学(OOSE/Object Oriented Software Engineering)を元に1990年頃に 発生し、ブーチのBooch法(どちらかというとOOD(Object Oriented Design)中心)の考えをまとめ、 UML(Unified Modeling Language)としてでてきた。


UMLでよく使われる図を列記すると、以下の物が挙げられる。


    

  • 構造図

      

    • クラス図
      • 

    • コンポーネント図
      • 

    • 配置図
      • 

    • オブジェクト図
      • 

    • パッケージ図
      • 

    

    • 

  • 振る舞い図

      

    • アクティビティ図
      • 

    • ユースケース図
      • 

    • ステートチャート図(状態遷移図)
      • 

    • 相互作用図
      • 

    • シーケンス図
      • 

    • コミュニケーション図(コラボレーション図)
      • 

    

    • 



その他の関連雑談のためのリンク



 









	
Linux環境の使い方

	

		2025年6月13日 	

	
unixにおけるセキュリティ


    

  • /etc/passwd , /etc/group , /etc/shadow

      

    • デバイスファイルとグループアクセス権

        

      • ls -al /dev/ttyUSB0
        • 

      • crw-rw—- 1 root dialout 188, 0  6月 13 04:00 ttyUSB0
        • 

      • sudo adduser user dialout
        • 

      

      • 

    

    • 

  • sudo

      

    • 元々は su コマンドを使うことが多かった
      • 

    • システム管理者になって作業

        

      • sudo bash で作業は危険
        • 

      

      • 

    • /etc/sudoers , sudoers.d

        

      • sudo adduser user sudo # sudoグループに user を追加
        • 

      • sudo vi /etc/sudoers
        
%sudo ALL=(ALL:ALL) NOPASSWD: ALL
        

          

        • sudoers ファイルを書き間違えると、sudo 自体が使えなくなるので要注意
          • 

        

        • 

      

      • 

    

    • 

  • suid

      

    • ファイル所有者権限でコマンドを実行
      • 

    • sudo chown root /usr/local/bin/foobar
      • 

    • sudo chmod u+s /usr/local/bin/foobar
      • 

    

    • 



リモートシステムの使い方


    

  • ssh

      

    • ssh-keygen 秘密鍵・公開鍵を作る
      • 

    • ssh-copy-id user@remoteserver 公開鍵をリモートサーバにコピー

        

      • パスワードなしでログインできる。
        • 

      

      • 

    • $HOME/.ssh ディレクトリは rwx,—,— になっていること
      • 

    • ssh remoteserver ls   # リモートサーバで ls を実行
      • 

    

    • 

  • ssh X11 foward

      

    • ssh 経由で GUI を利用することができる
      • 

    • Windows であれば WSL2 , macOS であれば XQuartz をインストールしておくこと

        

      • WSL2 Ubuntu 24 LTS が無難
        • 

      

      • 

    • local$ slogin -X remoteserver  # X11forward つきでログイン
      • 

    • remote$ echo $DISPLAY
      • 

    • remote$ xeyes   # X11経由で local の X11 に
      • 

    

    • 



管理コマンド


    

  • sudo apt update
    • 

  • sudo apt upgrade
    • 

  • apt search パッケージを探す
    • 

  • sudo apt install パッケージ名

      

    • sudo apt install nodejs
      • 

    • npm install JavaScriptパッケージ
      • 

    • sudo apt install python3
      • 

    • pip install Pythonパッケージ
      • 

    

    • 



VSCode


    

  • Japanese Language Pack for Visual Studio Code
    • 

  • Remote – SSH
    • 










	
Webプログラミングとセキュリティ

	

		2025年6月10日 	

	
ここまでの授業では、Webを使った情報公開で使われる、HTML , JavaScirpt , PHP , SQL などの解説を行ってきたが、これらを組み合わせたシステムを構築する場合には、セキュリティについても配慮が必要である。


今回は、初心者向けの情報セキュリティの講習で使われるCTFという競技の練習問題をつかって、ここまで説明してきた Web の仕組みを使ったセキュリティの問題について解説を行う。











	
派生や集約と多重継承

	

		2025年6月10日 	

	
派生や継承について、一通りの説明が終わったので、データ構造(クラスの構造)の定義の方法にも様々な考え方があり、どのように実装すべきかの問題点を考えるための説明を行う。その中で特殊な継承の問題についても解説する。


動物・鳥類・哺乳類クラス


派生や継承を使うと、親子関係のあるデータ構造をうまく表現できることを、ここまでの授業で示してきた。


しかしながら、以下に述べるような例では、問題が発生する。


// 動物クラス
class Animal {
private:
  char name[ 10 ] ;
public:
  Animal( const char s[] ) {
    strcpy( name , s ) ;
  }
  const char* get_name() const { return name ; }
  virtual void move() = 0 ;
  virtual void birth() = 0 ;
} ;

// 鳥類クラス
class Bird : public Animal {
public:
  Bird( const char s[] ) : Animal( s ) {}
  virtual void move() {
    printf( "%s fry.\n" , get_name() ) ;
  }
  virtual void birth() {
    printf( "%s lay egg.\n" , get_name() ) ;
  }
} ;

// 哺乳類クラス
class Mammal : public Animal {
public:
  Mammal( const char s[] ) : Animal( s ) {}
  virtual void move() {
    printf( "%s walk.\n" , get_name() ) ;
  }
  virtual void birth() {
    printf( "%s lay baby.\n" , get_name() ) ;
  }
} ;

int main() {
  Bird chiken( "piyo" ) ;
  chiken.move() ;
  chiken.birth() ;
  Mammal cat( "tama" ) ;
  cat.move() ;
  cat.birth() ;
  return 0 ;
}



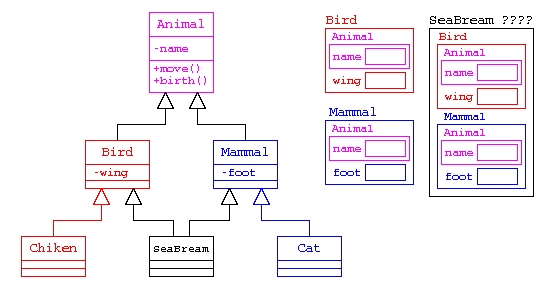
ここで、カモノハシを作るのであれば、どうすれば良いだろうか？


鳥類・哺乳類とは別にカモノハシを作る(いちばん無難な方法)


class SeaBream : public Animal {
public:
  Mammal( const char s[] ) : Animal( s ) {}
  virtual void move() {
    printf( "%s walk.\n" , get_name() ) ;
  }
  virtual void birth() {
    printf( "%s lay egg.\n" , get_name() ) ;
  }
} ;



この例では、簡単な処理だが、move() の中身が複雑であれば、改めて move() を宣言するのではなく、継承するだけの書き方ができないだろうか？


多重継承を使う方法(ダイヤモンド型継承が発生する)


C++ には、複数のクラスから、派生する多重継承という機能がある。であれば、鳥類と哺乳類から進化したのだから、以下のように書きたい。


// 多重継承 鳥(Bird)と哺乳類(Mammal) から SeaBeam を作る
class SeaBream : public Bird , public Mammal {
   //
} ;



しかし、カモノハシに move() を呼び出すと、鳥類の move() と哺乳類の move() のどちらを動かすか曖昧になる。


また「派生」は、基底クラスと派生クラスの両方のデータを持つデータ構造を作る。このため、単純に多重継承を行うと、カモノハシのクラスでは、派生クラスは親クラスのデータ領域と、派生クラスのデータ領域を持つため、鳥類の name[] と、哺乳類の name[] を二つ持つことになる。多重継承による”ダイヤモンド型継承”の問題




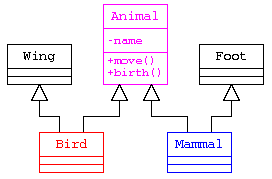
足と羽のクラスを作る場合(本来は多重継承で実装すべきではない)


以下に、足と羽のクラスを作ったうえで、多重継承を行うプログラム例を示す。


しかし、この例では、相変わらずカモノハシのクラスを多重継承で実装すると、ダイヤモンド型継承の問題が残る。


class Animal {
private:
  char name[ 10 ] ;
public:
  Animal( const char s[] ) {
    strcpy( name , s ) ;
  }
  const char* get_name() const { return name ; }
  virtual void move() = 0 ;
} ;
// 羽
class Wing {
public:
   const char* move_method() { return "fly" ; }
} ;
// 
class Leg {
public:
   const char* move_method() { return "walk" ; }
} ;
class Bird : public Animal , public Wind {
public:
  Bird( const char s[] ) : Animal( s ) {}
  virtual void move() {
    printf( "%s %s.\n" , get_name() , move_method() ) ;
  }
} ;
class Mammal : public Animal , public Leg {
public:
  Mammal( const char s[] ) : Animal( s ) {}
  virtual void move() {
    printf( "%s %s.\n" , get_name() , move_method() ) ;
  }
} ;






継承を使うべきか、部品として持つべきか


ただし、ここで述べた方式は、UML による設計の際に改めて説明を行うが、is-a , has-a の関係でいうなら、


    

  • Bird is a Animal. – 鳥は動物である。

      

    • “Bird has a Animal” はおかしい。
      • 

    • 鳥は、動物から派生させるのが正しい。
      • 

    

    • 

  • Bird has a Wing. – 鳥は羽をもつ。

      

    • “Bird is a Wing” はおかしい。
      • 

    • 鳥は、羽を部品として持つべき。
      • 

    

    • 



であることから、Wing は 継承で実装するのではなく、集約もしくはコンポジションのような部品として実装すべきである。


このカモノハシ問題をどうしても多重継承で実装したいのなら、C++では、以下のような方法で、ダイヤモンド型の継承問題を解決できる。


class Animal {
private:
   char name[ 10 ] ;
public:
   Animal( const char s[] ) {
      strcpy( name , s ) ;
   }
   const char* get_name() const { return name ; }
   virtual void move() = 0 ;
   virtual void birth() = 0 ;
} ;

// 鳥類クラス
class Bird : public virtual Animal {
public:
   Bird( const char s[] ) : Animal( s ) {}
   virtual void move() {
      printf( "%s fry.\n" , get_name() ) ;
   }
   virtual void birth() {
      printf( "%s lay egg.\n" , get_name() ) ;
   }
} ;

// 哺乳類クラス
class Mammal : public virtual Animal {
public:
   Mammal( const char s[] ) : Animal( s ) {}
   virtual void move() {
      printf( "%s walk.\n" , get_name() ) ;
   }
   virtual void birth() {
      printf( "%s lay baby.\n" , get_name() ) ;
   }
} ;

class SeaBream : public virtual Bird , virtual Mammal {
public:
   SeaBream( const char s[] ) : Animal( s ) {}
   void move() {
      Mammal::move() ;
   }
   void birth() {
      Bird::birth() ;
   }
} ;



ただし、多重継承は親クラスの情報と、メソッドを継承する。この場合、通常だと name[] を二つ持つことになるので、問題が発生する。そこで、親クラスの継承に virtual を指定することで、ダイヤモンド型継承の ２つの属性をうまく処理してくれるようになる。


しかし、多重継承は処理の曖昧さや効率の悪さもあることから、採用されていないオブジェクト指向言語も多い。特に Java は、多重継承を使えない。その代わりに interface という機能が使えるようになっている。


多重継承を使える CLOS や Python では、適用するメソッドやインスタンス変数の曖昧さについては親クラスへの優先度を明確にできる機能がある。曖昧さの問題を避けるのであればクラス限定子”::”を使うべきである。









	
Javaでリスト構造

	

		2025年6月9日 	

	
テスト前のリスト導入の復習


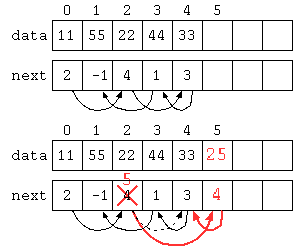
前回のリスト構造の導入では、配列のデータに次のデータの入っている番号を添えることで途中にデータを挿入できるデータ構造の説明をした。


また、それをクラスを用いたプログラムを示した。


ヒープメモリとは


Javaでは、すべてのオブジェクトはヒープメモリに保存する。


ヒープメモリとは、一時的なデータの保管場所であり、new 演算子でデータを保存する場所を確保する。


Javaでは、分かり難いのでC言語で説明を行う。malloc() は、指定されたバイト数のメモリをヒープ領域に確保する命令。malloc() に失敗すると、NULL が返ってくる。また、使い終わったら malloc() の領域は free() 命令で返却が必要となる。


((( 配列をヒープメモリで確保 )))
#include <stdio.h>
#include <stdlib.h>

int main() {
   int a[ 5 ] = { 1 , 2 , 3 , 4 , 5 } ;
   int* b ;
   if ( (b = (int*)malloc( sizeof( int ) * 5 )) != NULL ) {
      for( int i = 0 ; i < 5 ; i++ )
         b[ i ] = i + 1 ;
      free( b ) ;    // malloc() で確保したメモリ領域は返却が必要
   }
   return 0 ;
}

((( オブジェクトをヒープメモリに確保 )))
struct Complex {
   double re ;
   double im ;
} ;
int main() {
   struct Complex* c ;
   if ( (c = (struct Complex*)malloc( sizeof( struct Complex ) )) != NULL ) {
      c->re = 1.23 ;
      c->im = 2.34 ;
      free( c ) ;
      return 0 ;
   } else {
      printf( "No heap memory\n" ) ;
      return 1 ;
   }
}

((( 上記C言語をJavaで書くと )))
class Complex {
   double re ;
   double im ;
   Complex( double r , double i ) {
      this.re = r ;
      this.im = i ;
   }
}

public class Main {
   public static void main( String[] args ) {
      try {
         Complex c = new Complex( 1.23 , 2.34 ) ;
                    // Javaではヒープメモリが確保に失敗したら、
                    // OutOfMemoryErrorの例外が発生する。

         c = null ; // free()はJavaでは不要
                    // nullを代入してもいい。
      } catch( OutOfMemoryError e ) {
         System.out.println( "No heap memory" ) ;
         System.exit( 1 ) ;
      }
   }
}


リスト構造 ListNode


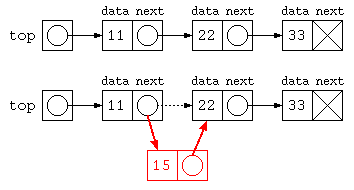
前述の data と next で次々とデータを続けて保存する方法を、next の部分を次のデータへの参照を用いるように、リスト構造(連結リスト)を定義する。


import java.util.*;

class ListNode {
    int      data ;   // データ部分
    ListNode next ;   // 次のデータへの参照
    // コンストラクタ
    ListNode( int d , ListNode nx ) {
        this.data = d ;
        this.next = nx ;
    }
} ;

public class Main {
    public static void main(String[] args) throws Exception {
        ListNode top = new ListNode( 11 , new ListNode( 22 , new ListNode( 33 , null ) ) ) ;

        for( ListNode p = top ; p != null ; p = p.next )
            System.out.println( p.data ) ;
        // 途中にデータを入れる
        top.next = new ListNode( 15 , top.next ) ;

        for( ListNode p = top ; p != null ; p = p.next )
            System.out.println( p.data ) ;
    }
}





リスト操作


リスト構造に慣れるために簡単な練習をしてみよう。リスト構造のデータに対するメソッドをいくつか作ってみよう。print() や sum() を参考に、データ数を求める count() , 最大値を求める max() , データを検索する find() を完成させてみよう。


class ListNode {
    (略)
} ;

public class Main {
    static void print( ListNode p ) {   // リストを表示
        for( ; p != null ; p = p.next )
            System.out.print( p.data + " " ) ;
        System.out.println() ;
    }

    static int sum( ListNode p ) {      // リストの合計を求める
        int s = 0 ;
        for( ; p != null ; p = p.next )
            s += p.data ;
        return s ;
    }

    static int count( ListNode p ) {    // データ件数を数える

    }

    static int max( ListNode p ) {      // データの最大値を求める

    }

    static boolean find( ListNode p , int key ) { // データ列の中から特定のデータを探す
                                                  //   見つかったら true , 見つからなければ false
    }
    public static void main(String[] args) throws Exception {
        ListNode top = new ListNode( 11 , new ListNode( 22 , new ListNode( 33 , null ) ) ) ;
        print( top ) ;
        System.out.println( "合計:" + sum( top ) ) ;
        System.out.println( "件数:" + count( top ) ) ;
        System.out.println( "最大:" + max( top ) ) ;
        System.out.println( "検索:" + (find( top , 22 )
                                       ? "みつかった" : "みつからない" ) ) ;
    }
}



オブジェクト指向っぽく書いてみる


前述のプログラムでは、print( top ) のように使う static な関数としてプログラムを書いていた。しかし、オブジェクト指向であれば、オブジェクトに対するメソッドだと top.print() のように書きたい。この場合だと、以下のように書くかもしれない。


import java.util.*;

class ListNode {
    int data ;
    ListNode next ;
    ListNode( int d , ListNode n ) {
        this.data = d ;
        this.next = n ;
    }
    void print() {   // リストの全データを表示
        for( ListNode p = this ; p != null ; p = p.next )
            System.out.print( p.data + " " ) ;
        System.out.println() ;
    }
    int sum() {    // リストの合計を求める
        int  s = 0 ;
        for( ListNode p = this ; p != null ; p = p.next )
            s += p.data ;
        return s ;
    }
} ;

public class Main {
    public static void main(String[] args) throws Exception {
        ListNode top = new ListNode( 11 , new ListNode( 22 , new ListNode( 33 , null ) ) ) ;
        top.print() ;
        System.out.println( "合計: " + top.sum() ) ;

        ListNode list_empty = null ;
        list_empty.print() ;  // 実行時エラー java.lang.NullPointerException ぬるぽ！
    }
}



しかし、データ件数 0件 に対してメソッドを呼び出せない。


ListNode と List というクラスで書いてみる


ひとつの方法として、リストの先頭だけのデータ構造を宣言する方法もある。


class ListNode {
    int   data ;
    ListNode next ;
    ListNode( int d , ListNode n ) {
        this.data = d ;
        this.next = n ;
    }
} ;

class List {
    ListNode top ;
    List( ListNode p ) {
        this.top = p ;
    }
    void print() {
        for( ListNode p = top ; p != null ; p = p.next )
            System.out.print( p.data + " " ) ;
        System.out.println() ;
    }
} ;

public class Main {
    public static void main(String[] args) throws Exception {
        List list = new List( new ListNode( 11 , new ListNode( 22 , new ListNode( 33 , null ) ) ) ) ;
        list.print() ;
        
        List list_empty = new List( null ) ;
        list_empty.print() ;
    }
}





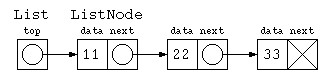
しかし、List と ListNode の2つのデータの型でプログラムを書くのは面倒くさい。


授業ではシンプルに説明したいので、今後はこの方法は極力避けていく。


先頭にダミーデータを入れる


複数のクラス宣言するぐらいなら、リストデータの先頭は必ずダミーにしておく方法もあるだろう。


import java.util.*;

class ListNode {
    int data ;
    ListNode next ;
    ListNode( int d , ListNode n ) {
        this.data = d ;
        this.next = n ;
    }
    void print() {   // リストの全データを表示
        for( ListNode p = this.next ; p != null ; p = p.next )
            System.out.print( p.data + " " ) ;
        System.out.println() ;
    }
} ;

public class Main {
    public static void main(String[] args) throws Exception {
        ListNode list = new ListNode( -1 , null ) ;
        list.next = new ListNode( 11 , new ListNode( 22 , new ListNode( 33 , null ) ) ) ;
        top.print() ;
        System.out.println( "合計: " + top.sum() ) ;

        ListNode list_empty = new ListNode( -1 , null ) ;
        list_empty.print() ;
    }
}





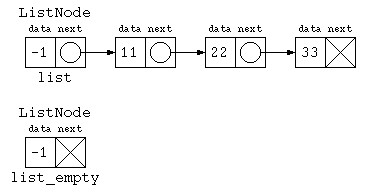
以降、必要に応じて、先頭にダミーを入れる手法も取り混ぜながらプログラムを書くこととする。


入力データをリストに追加


入力しながらデータをリストに格納する処理を考えてみる。


リストでデータを追加保存するのであれば、一番簡単なプログラムは、以下のように先頭にデータを入れていく方法だろう。


class ListNode {
    (略)
    void print() {
        for( ListNode p = this ; p != null ; p = p.next )
            System.out.print( p.data ) ;
        System.out.println() ;
    }
} ;
    
public class Main {
    public static void main(String[] args) throws Exception {
        int[] inputs = { 11 , 22 , 33 } ;
        ListNode top = null ;

        for( int datum : inputs )
            top = new ListNode( datum , top ) ;
        top.print() ;
    }
}





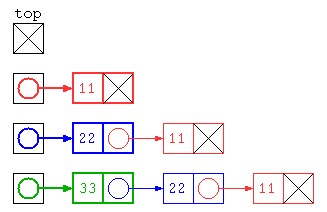
でもこの方法だと、先頭にデータを入れていくため、保存されたデータは逆順になってしまう。


末尾にデータを入れる


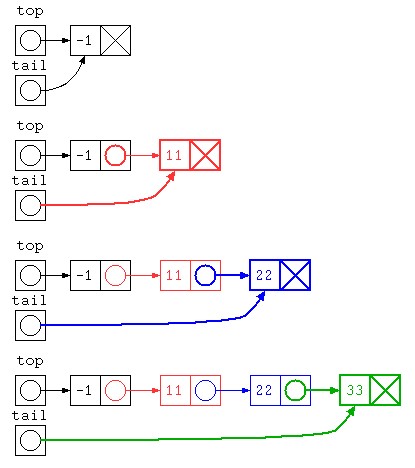
逆順になるのを避けるのであれば、データを末尾に追加する方法があるだろう。ただし初期状態でデータが0件だと処理が書きづらいので、先頭にダミーを入れておく方法で書いてみる。


public class Main {
    public static void main(String[] args) throws Exception {
        int[] test_data = { 11 , 22 , 33 } ;

        ListNode top = new ListNode( -1 , null ) ; // ダミー
        ListNode tail = top ;
        for( int x : test_data ) {
            tail.next = new ListNode( x , null ) ;
            tail = tail.next ;
        }
        top.print() ; // -1   11  22  33
    }                 // ダミー
}












	
バックエンドと所有権の設定

	

		2025年6月3日 	

	
前回の講義でファイルのパーミッション(読み書き権限)について確認したが、バックエンドプログラミングで必要となるファイルの所有権の設定を通して、演習を行う。これに合わせ、サーバ上のファイルの編集作業なども体験する。


サーバ上のファイルの編集


以前のバックエンドのプログラムの演習ではサーバの設定などの体験もできていないため、フロントエンドの処理でサーバ上に送られたデータは、最終的な書き込み処理は行っていなかった。今回は、サーバ上でデータをサーバ上のバックエンドプログラムの PHP ファイルを修正し、データが書き込めるようにプログラムの修正を行う。


サーバ上のファイルを編集するには、色々な方法がある。




サーバ上のエディタで直接編集


unix のシステムで直接ファイルを編集するのであれば、vim や emacs を利用するのが一般的であろう。これらのエディタはリモートサーバにsshなどでログインしている時は、端末ソフトの文字表示機能だけで動作し、GUI 機能を使わない。vim や emacs は、古くから使われ、Windows で動く vim や emacs もある。


システム管理者権限で編集する必要があるファイルの場合は、以下に紹介するような方法は煩雑であり、サーバ上で直接編集も知っておくべき。


プログラムをローカルPCで編集しアップロード(今回はコレ)


前回の演習では、リモートサーバに接続する際には ssh コマンドを用いたが、ssh にはファイル転送のための scp コマンドも用意されている。


scp コマンドは、通常の cp 命令 ( cp コピー元 コピー先 ) を ssh のプロトコルでリモートする機能を拡張したものであり、リモートのコンピュータをコピー元やコピー先として指定する場合は、 ユーザ名@リモートホスト:ファイル場所 と記載する。




# remotehostのファイル helloworld.c をローカルホストのカレントディレクトリ.にダウンロード
C:\Users\tsaitoh> scp tsaitoh@remotehost:helloworld.c .  
# ローカルホストの foobar.php を remotehostの/home/tsaitoh/public_html/ フォルダにアップロード
C:\Users\tsaitoh> scp foobar.php tsaitoh@remotehost:/home/tsaitoh/public_html/





VSCode でリモートファイルを編集


最近のエディタでは、前述のローカルPCで編集しアップロードといった作業を、自動的に行う機能が利用できる。emacs の tramp-mode や、VS Code の Remote ssh プラグインなどがこれにあたる。利用する演習用のサーバが高機能であれば、vscode + remote-ssh が一番便利と思われるが、remote-ssh はサーバで大きな node.js を動かすため、サーバ負担が大きいので今回はこの方式は使わない。




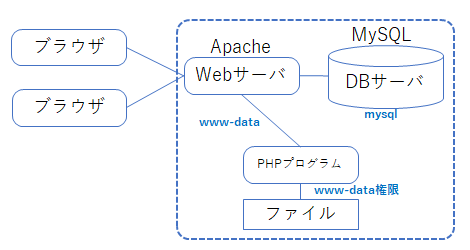
Webアプリと所有権の問題


PHPで書かれたバックエンドでのプログラムにおいて、Webサーバは www-data(uid),www-data(groupid) というユーザ権限で動作している。そして、webサーバと連動して動く PHP のプログラムも www-data の権限で動作する。一方で、通常ユーザが開発しているプログラムが置かれる $HOME/public_html フォルダは、何もしなければそのユーザのものである。このため、PHP のプログラムがユーザのフォルダ内にアクセスする際には、www-data に対してのアクセス権限が必要となる。


Windows ユーザが Web プログラミングの体験をする際には、XAMPP などのパッケージを利用することも多いだろう。しかし XAMPP などは、中身のWebサーバ(apache), DBサーバ(MySQL)などすべてがインストールしたユーザ権限で動いたりするため、所有権の設定の知識が無くても簡単に利用することができる(あるいはユーザ自身が管理者権限を持っているため設定が無くてもアクセス権問題が発生しない)。このため Linux 環境での Web プログラミングに移行する際に、ユーザ権限の設定を忘れ、プログラムが動かず戸惑うことも多い。


今回の演習では、管理者権限で動いている自分のパソコンの中のXAMPPを使わず、複数のユーザで動いている演習用サーバを用いる。


データベースサーバの場合


また、データの保存でデータベースを利用する場合、Oracle や MySQL といった、ネットワーク型のデータベースでは、Webサーバとは別にデータベースのサーバプログラムが動作している。ネットワーク型のデータベースでは、様々なユーザ・アプリケーションがデータの読み書きを行うため、SQL の create user 命令でユーザを割り当て、grant 命令でユーザのデータへのアクセス権限を指定する。




Webアプリは、データベースのサーバに接続する際には、ユーザ名とパスワードが必要となる。


簡易データベースSQLiteの場合


簡単なデータベースシステムの SQLite は、PHP の SQLite プラグインを経由してディレクトリ内のファイルにアクセスする。このため、データベースファイルやデータベースのファイルが置かれているフォルダへのアクセス権限が必要となる。今回の演習用サーバでは、ゲストアカウントは www-data グループに所属しているので、データベースファイルやフォルダに対し、www-data グループへの書き込み権限を与える。


chown , chgrp , chmod コマンド


ファイル所有者やグループを変更する場合には、chown (change owner) 命令や chgrp (change group) 命令を使用する。ただし、chown はシステム管理者権限(root)でなければ使えない。chgrp も自分が所有してかつ変更後のグループに加入していなければ使えない。


chown ユーザID ファイル
　例： $ chown tsaitoh helloworld.c
chgrp グループID ファイル
　例： $ chgrp www-data public_html



ファイルに対するパーミッション(利用権限)を変更するには、chmod (change mode) 命令を用いる。

chmod 命令では、読み書きの権限は2進数3桁の組み合わせで扱う。読書可 “rw-“ = 6, 読出可 = “r–“ = 4 , ディレクトリの読み書き可 “rwx” = 7 など。ファイルには、所有者,グループ,その他の3つに分けて、読み書きの権限を割り当てる。2進数3桁=8進数1桁で表現できることから、一般的なファイルの “rw-,r–,r–“ は、8進数3桁 で 644 , ディレクトリなら “rwx,r-x,r-x” は 755 といった値で表現する。


chmod 権限 ファイル
　例： $ chmod 664 helloworld.c
       $ ls -al
       -rw-rw-r-- tsaitoh ei        123 5月20 12:34 helloworld.c
       $ chmod 775 public_html
       drwxrwxr-x tsaitoh www-data 4096 5月20 12:34 public_html
  8進数表現を使わない場合
       $ chmod u+w,g+w helloworld.c
               ユーザ(u)への書き込み権限,グループ(g)への書き込み権限の追加(+)
       $ chmod g-w,o-rw helloworld.c
               グループ(g)書き込み権限を消す、その他(o)の読み書き権限を消す(-)
       $ chmod u=rw,g=r,o=r helloworld.c
               ユーザ(u)への読み書き,グループ(g),その他(o)への読み出し権限を設定(=)


演習内容


前回の演習と同じ方法でサーバにログインし、サーバ上で直接ファイル編集をしてみよう。


C:\Users\tsaitoh> ssh -P 443 guest00@nitfcei.mydns.jp
$ ls -al
-rw-r--r-- 1 guest00 root 76 Mar 8 12:06 helloworld.c
$ vi helloworld.c
もしくは
$ emacs helloworld.c




vim の使い方


挿入 iテキストESC

削除 x

ファイルの保存 :w

エディタの修了 ZZ






emacs の使い方


ファイルの保存 Ctrl-X Ctrl-S

エディタの修了 Ctrl-X Ctrl-C




GitHubから演習ファイルを複製


GitHub は、複数の開発者が共同でプログラムを開発するための環境で、プログラムの情報共有などに広く使われている。ファイルは、git コマンドで複製や更新ができる。


(( public_html の中に演習用ファイルを github からダウンロード ))
$ cd ~/public_html
public_html$ git clone https://github.com/tohrusaitoh/recp.git
public_html/recp$ cd recp/
public_html/recp$ ls -al
-rw-r--r-- 1 t-saitoh home 870 11月 10 2021 Makefile
-rw-r--r-- 1 t-saitoh home 1152 10月 8 2021 README.md
 :


サーバ上のファイルをパソコンにコピーして編集


(( サーバ上のファイル sampleI.php (sample-アイ.php) をダウンロード ))
C:\Users\tsaitoh> scp -P 443 guest00@nitfcei.mydns.jp:public_html/recp/sampleI.php .

VSCode などのエディタで編集

(( 編集した sampleI.php をサーバにアップロード ))
C:\Users\tsaitoh> scp -P 443 sampleI.php guest00@nitfcei.mydns.jp:public_html/recp/




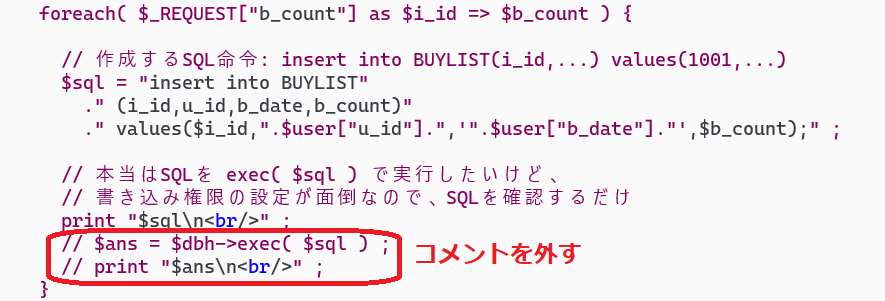
Webサーバで書き込みができるように設定


(( public_html のデータベースファイル shopping.db を書き込み可能にする ))
$ chgrp www-data ~guest00/public_html/recp/shopping.db
$ chmod g+w ~guest00/public_html/recp/shopping.db

(( public_html/recp フォルダを書き込み可能にする ))
$ chgrp www-data ~guest00/public_html/recp
$ chmod g+w ~guest00/public_html/recp


バックエンドプログラムを実行してみる


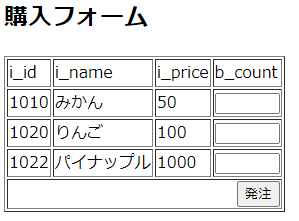
パソコンのブラウザで、http://nitfcei.mydns.jp/~guest00/recp/sampleI.php を開く。


  


書き込み結果を確認してみる


(( データベースファイル shopping.db の書込み結果を確認 ))
$ cd ~guest00/public_html/recp
public_html/recp$ sqlite3 shopping.db
SQLite version 3.31.1 2020-01-27 19:55:54
Enter ".help" for usage hints.
sqlite> select * from BUYLIST ;
1010|10001|2021-11-05|1
1020|10001|2021-11-05|2
1022|10001|2021-11-05|3
  :
sqlite> [Ctrl-D] コントロールDで sqlite3 を抜ける
public_html/recp$










	
テスト返却と追加説明

	

		2025年6月2日 	

	
前期中間試験の返却に伴い、補足説明。


C言語,Javaにおける文の定義


テストの時に、下記のようなプログラムで piyo() は、for の範囲？みたいな質問があったので、補足説明


for( ... ; ... ; ... )
   if ( ... )
      foo = bar ;
   else {
      baz() ;
      hoge() ;
   }
piyo() ;



C言語やJavaにおける文の定義は、以下の通り


文 ::= 式 ;    // 単文
     | ;       // 空文
     | { 文 文 ... }        // 複文
     | for( .. ; .. ; .. ) 文   // 制御構文
     | do 文 while( 式 ) ;
     | if ( 式 ) 文 [ else 文 ]
     ;


こういった文の範囲の誤解を避けるためのものが、インデント。


正しいインデントをつける習慣が重要。



Javaにおけるクラスとデータ構造のイメージ


この後のリスト構造の説明でもオブジェクトがどのように保存されるかを理解するのは重要なので、オブジェクトの説明。


Java では、class 宣言されたデータ構造は、ヒープメモリと呼ばれるデータ領域に保存されている。


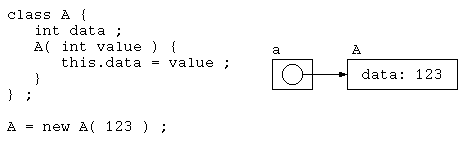
class A {
   int data ;
   A( int value ) {
      this.data = value ;
   }
} ;

public class Main {
   public static void main( String[] args ) {
      A a = new A( 123 ) ;
   }
}



ここで、new 演算子は、指定されたオブジェクトをヒープメモリ上に確保する。そして、そのデータの入っている領域アドレスを、インスタンスの変数 a に代入している。




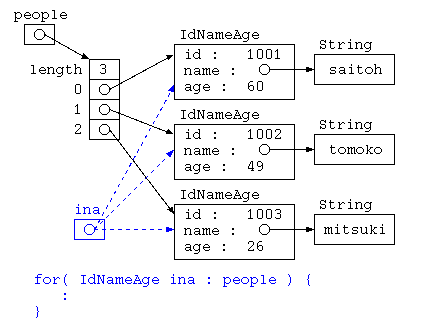
テストで出題した例であれば、


class IdNameAge {
   int    id ;
   String name ;
   Age    age ;
   IdNameAge( int i , String n , int a ) {
      this.id   = i ;
      this.name = n ;
      this.age  = a ;
   }
} ;

IdNameAge[] = people = {
   new IdNameAge( 1001 , "saitoh" ,  60 ) ,
   new IdNameAge( 1002 , "tomoko" ,  49 ) ,
   new IdNameAge( 1003 , "mitsuki" , 26 ) ,
} ;





Integer 型も、整数データを記憶するけど、オブジェクト型である。




ただし、Integer 型を常にヒープメモリに保存するのは、効率が悪いので、-128～127までの値ではIntegerオブジェクトは内部でキャッシュされる。Integer y = 123 ; 書いてはいるけど本来であれば、Integer y = new Integer( 123 ) ;  と書く必要があった。しかしJava5以降に、オートボクシングと呼ばれる機能があるため Integer y = 123 のように書けるし、こう書く方が推奨されている。


public class Main {
    public static void main(String[] args) {
        // Your code here!
        Integer sx = 123 ;
        Integer sy = 123 ;
        System.out.println( sx == sy ) ; // true
        Integer fx = 12345 ;
        Integer fy = 12345 ;
        System.out.println( fx == fy ) ; // false
    }
}










	
寮生が地区体育祭に参加

	

		2025年6月2日 	

	
学寮のある鯖江市・豊地区の地区体育祭に、青武台チームにて参加しました。




手伝ってくれた寮生は、体育祭を盛り上げるような声出しもしながら、リレーや大縄跳びに参加し、青武台の方たちとの交流のいい機会となりました。参加してくれた3人の寮生の皆さん、感謝ですぅ。私も、玉入れ(じぃさん枠競技)に参加して、すこしばかり貢献した…か…な…。


{CAPTION}









	
白詰草の冠

	

		2025年5月30日 	

	
学生♂が作った白詰草の冠で、何故か写真を撮られるジジィ。


{CAPTION}








	

		投稿ナビゲーション	

	← 過去の投稿	 新しい投稿 →	




	


	

		
システム




最新の投稿(電子情報)

	



アーカイブ
		
		

			

カテゴリー