Error Establishing a Database Connection
びびった。
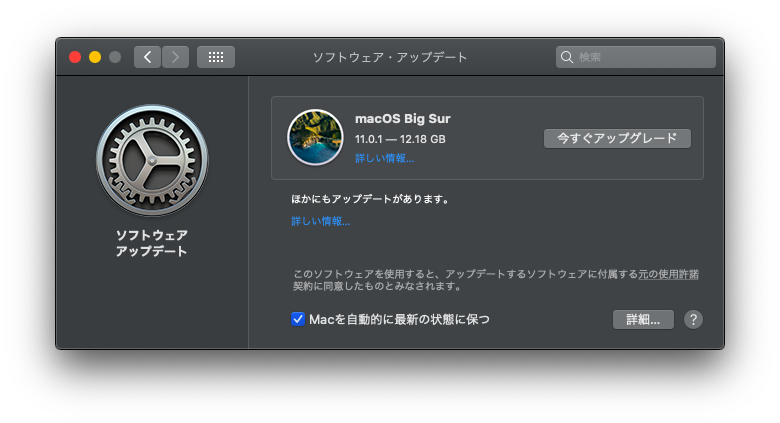
この WordPress で、特に何もしていないのに、「データベース接続の確立エラー」(Error Establishing a Database Connection)
が表示された。コレが出ると、データベースファイルが壊れたとかの場合が多くて、復旧に手間取る可能性が高い。
今回は、サーバに login して、MySQL の Restart だけで復帰した。
オブジェクト指向プログラミング2020全講義録
専攻科2年オブジェクト指向プログラミングの2020年度の講義録の一覧
情報制御基礎2020全講義録
3年学際科目・情報制御基礎の2020年度の講義録の一覧
2020年度前期授業アンケート
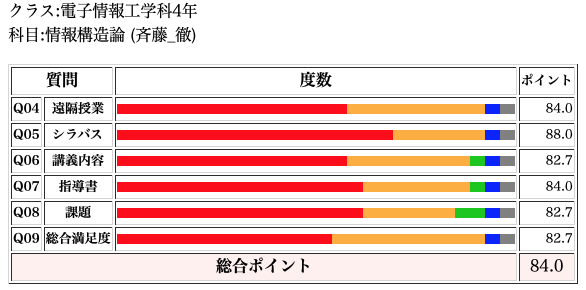
情報構造論
情報構造論は通年科目なので、中間状況だけど、ひとまず80ポイント越え。1件だけ最低評価が並んでいるのが気がかり。不満のある人が積極的に質問してくれるといいのだが。
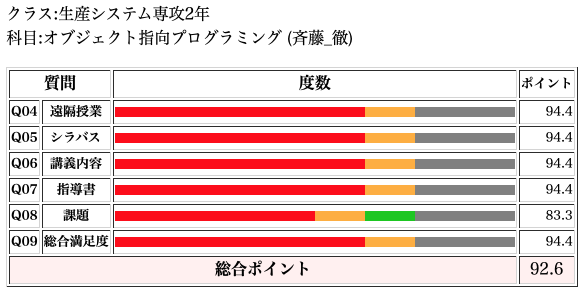
オブジェクト指向プログラミング
オブジェクト指向は、専攻科2年相手の前期科目。課題でやや不満が1件あるけど、難しかったのだろうか。設定が曖昧だったのだろうか。
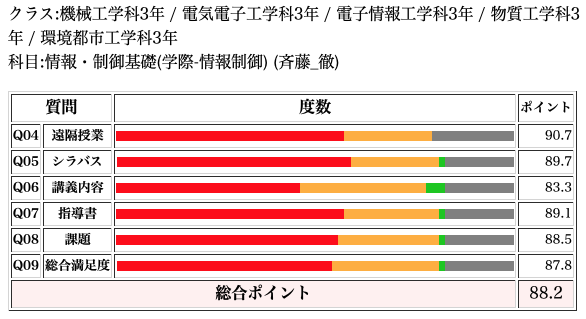
情報制御基礎
情報制御基礎は、3年生の学際科目で全学科対象の授業。「テストの過去問題がWebに掲載してあり勉強しやすかった」といった趣旨の意見もあり、評価も高かった。
どの授業も、コロナによる遠隔授業であったが、例年 Web に掲載している講義資料をそのまま使い、Teams のWeb会議でMicrosoft Edge のペン書き機能を使いながら補足説明を書き込みしながら行なった。Web会議は録画しておき、オンデマンドで視聴できるようにしておいたので、コロナ遠隔授業といいながらも、授業の進め方は今まで通りにすすめたつもり。
AVLと2分ヒープ
前回、2分探索木へのデータ追加の説明と、演習課題を行っていたが、演習時間としては短いので、今日も前半講義で残り時間は演習とする。
2分探索木へのデータ追加と不均一な木の成長
先週の講義で説明していた、entry() では、データを追加すべき末端を探し、追加する処理であった。
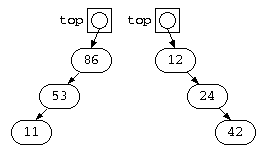
しかし、前回のプログラムで、以下のような順序でデータを与えたら、どのような木が出来上がるであろうか?
- 86, 53, 11 – 降順のデータ
- 12, 24, 42 – 昇順のデータ
この順序でデータが与えられると、以下のような木が出来上がってしまう。このような木では、データを探しても1回の比較でもデータ件数が1つ減るだけで、O(N)となってしまう。通常のデタラメな順序でデータが与えられれば、木はほぼ左右均等に成長するはずである。
AVL木
このような、不均一な木が出来上がっても、ポインタの繋ぎ変えで検索回数を改善できる。例えば、以下のような木では、赤の左側に偏っている。
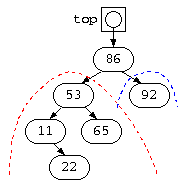
このような場合でも、最初、青の状態であっても、不均一な部分で赤のようなポインタの繋ぎ変えを行えば、木の段数を均一に近づけることができる。この例では、11,65,92の木が、右回転して 11 の木の位置が上がっている。(右回転)
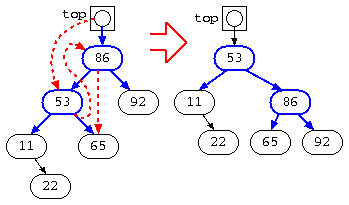
この様に、左右の枝の大きさが不均一な場所を見つけ、右回転や左回転を行う処理を繰り返すことで、段数が均一な2分探索木に修正ができる。この様な処理でバランスの良い木に修正された木は、AVL木と呼ばれる。
理解確認
- 木の根からの段数を求める関数 tree_depth() を作成せよ。
例えば、上のAVL木の説明の図であれば、4段なので4を返すこと。
// 木の段数を数える関数
_____ tree_depth( _______________ p ) {
if ( p == NULL ) {
return _____ ;
} else {
int d_L = ______________ ;
int d_R = ______________ ;
if ( d_L > d_R )
return _____ ;
else
return _____ :
}
}
// pをつなぎ替え上部を返り値で返す。
struct Tree*rot_right( struct Tree* p ) {
// p
// / \
// pl
// / \
// pr
struct Tree* pl = p->left ;
struct Tree* pr = pl->right ;
pl->right = p ;
p->left = pr ;
return pl ;
}
int main() {
printf( "%d¥n" , tree_depth( top ) ) ;
top = rot_right( top ) ;
return 0 ;
}
2分ヒープ(binary heap)
2分探索木では、1つのノードにつき2つのポインタを持ち、データ1件あたりのメモリの使用量が多い。通常の「配列の先頭から昇順にデータを並べる2分探索法」では、途中にデータを挿入する場合、データを後ろにずらす必要があるため、O(N)の処理時間を要する。
これらの問題の解決法の1つとして、2分ヒープがある。左右に均一に成長している2分探索木で、上から番号を以下の様に振ると、i番目のデータの左の枝は 2×i+1 番目、右の枝は 2×i+2 番目であることが判る。(自分の親のノードは、(i-1)/2 番目)
このような順序で配列にデータを保存する方法が2分ヒープである。この方式ならアルゴリズムの説明は省略するが、O(log(N))で挿入が可能となる。
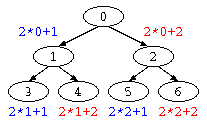
int a[ 7 ] = { 53 , 11 , 86 , 10 , 22 , 65 , 92 } ;
// 2分ヒープを表示
void print_heap( int array[] , int idx , int size ) {
if ( idx < size ) {
// 左の枝を表示
print_heap( array , 2*idx + 1 , size ) ;
// 真ん中の枝を表示
printf( "%d " , array[ idx ] ) ;
// 右の枝を表示
print_heap( array , 2*idx + 2 , size ) ;
}
}
// 2分ヒープから key を検索
int find_heap( int array[] , int idx , int size , int key ) {
while( idx < size ) {
if ( array[ idx ] == key )
return idx ; // 見つかったら配列の番号を返す
else if ( array[ idx ] _____ key ) // 何が入るか考えよう
idx = ________________ ;
else
idx = ________________ ;
}
return -1 ; // 見つからなかったら、-1 を返す
}
int main() {
print_heap( a , 0 , 7 ) ;
if ( find_heap( a , 0 , 7 , 65 ) >= 0 )
printf( "Find!!¥n" ) ;
return 0 ;
}
SQLと結合
前半にSQLの説明の後、後半はSQL実験環境を用いた演習時間とした。
SQLの基礎
前回の講義で、データベースでは、記録されているデータの読み書きは、SQL で行われ、射影・結合・選択を表す処理で構成されることを示した。SQL の機能を理解するために、同じ処理を C 言語で書いたらどうなるのかを示す。
SELECT S.業者番号 -- 必要とされるデータを抽出する射影 --
FROM S -- 複数のテーブルを組合せる結合 --
WHERE S.優良度 >= 20 ; -- 対象となるデータを選び出す選択 --
// 配列の個数を求める #define 文
#define sizeofarray(ARY) (sizeof(ARY) / sizeof(ARY[0]))
// C言語なら... S のデータを構造体宣言で書いてみる。
struct Table_S {
char 業者番号[ 6 ] ; // 当然、C言語では要素名を
char 業者名[ 22 ] ; // 漢字で宣言はできない。
int 優良度 ;
char 所在[ 16 ] ;
} S[] = {
{ "S1" , "ABC社" , 20 , "福井" } ,
:
} ;
// SELECT...をC言語で書いた場合の命令のイメージ
// 結合
for( int i = 0 ; i < sizeofarray( S ) ; i++ ) {
// 選択
if ( S[i].優良度 >= 20 )
// 射影
printf( "%d¥n" , S[i].業者番号 ) ;
}
Sは、テーブル名であり、文脈上対象テーブルが明らかな場合、フィールド名の前の テーブルは省略可能である。
SELECT 業者番号 FROM S WHERE 優良度 >= 20 ;
WHERE 節で記述できる条件式では、= , <>(not equal) , < , > , <= , >= の比較演算子が使える。
# これ以外の演算機能は、次週にて紹介予定。
直積と結合処理
ここで、SQLの最も便利な機能は、直積による結合処理。複数の表を組み合わせる処理。単純な表形式の関係データベースで、複雑なデータを表現できる基本機能となっている。
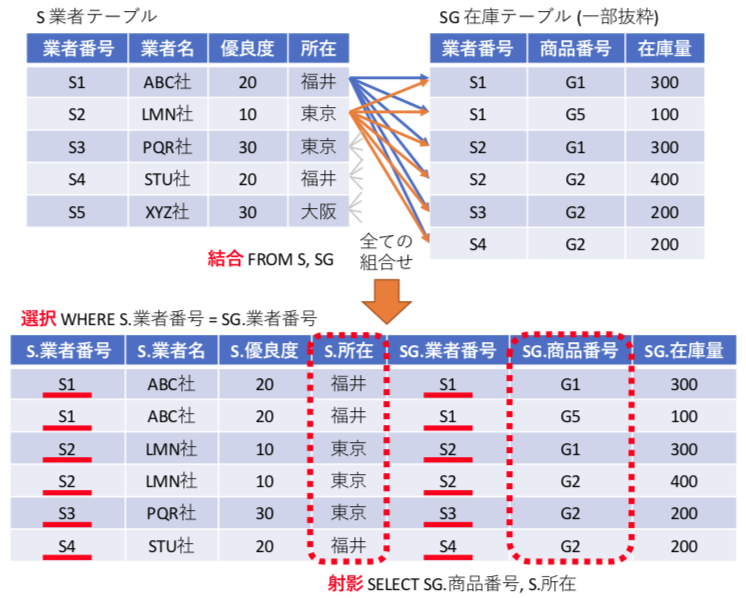
SELECT SG.商品番号 , S.所在 FROM S , SG WHERE SG.業者番号 = S.業者番号
- 実験環境で直積と結合処理(学内のみ)
上記の様に FROM 節に複数のテーブルを書くと、それぞれのテーブルの直積(要素の全ての組み合わせ)を生成する処理が行われる。この機能が結合となる。しかし、これだけでは意味がないので、通常は外部キーが一致するレコードでのみ処理を行うように、WHERE SG.業者番号 = S.業者番号 のような選択を記載する。最後に、結果として欲しいデータを抽出する射影を記載する。
// C言語なら
struct Table_S {
char 業者番号[ 6 ] ;
char 業者名[ 22 ] ;
int 優良度 ;
char 所在[ 16 ] ;
} S[] = {
{ "S1" , "ABC社" , 20 , "福井" } ,
:
} ;
struct Table_SG {
char 業者番号[ 6 ] ;
char 商品番号[ 6 ] ;
int 在庫量 ;
} = SG[] {
{ "S1" , "G1" , 300 } ,
:
} ;
// FROM S
for( int i = 0 ; i < sizeofarray( S ) ; i++ ) {
// FROM SG
for( int j = 0 ; j < sizeofarray( SG ) ; j++ ) {
// WHERE S.業者番号 = SG.業者番号
if ( strcmp( S[i].業者番号 , SG[j].業者番号 ) == 0 ) {
// SELECT SG.商品番号 , S.所在
printf( "%s %s¥n" , SG[j].商品番号 , S[i].所在 ) ;
}
}
}
(1) i,jの2重forループが、FROM節の結合に相当し、(2) ループ内のif文がWHERE節の選択に相当し、(3) printfの表示内容が射影に相当している。
射影の処理では、データの一部分を抽出することから、1件の抽出レコードが同じになることもある。この際の重複したデータを1つにまとめる場合には、DISTINCT を指定する。
SELECT DISTINCT SG.商品番号, S.所在 FROM S, SG WHERE SG.業者番号 = S.業者番号 ;
- 実験環境で結合/重複削除(学内のみ)
上記のプログラムでは、データの検索は単純 for ループで記載しているが、内部で HASH などが使われていると、昇順に処理が行われない場合も多い。出力されるデータの順序を指定したい場合には、ORDER BY … ASC (or DESC) を用いる
SELECT SG.商品番号, S.所在 FROM S, SG WHERE SG.業者番号 = S.業者番号 ORDER BY S.所在 ASC ; -- ASC:昇順 , DESC:降順 --
- 実験環境で結合/並び替え(学内のみ)
表型のデータと串刺し
FROM に記載する直積のための結合では、2つ以上のテーブルを指定しても良い。
SELECT S.業者名, G.商品名, SG.在庫量
FROM S, G, SG
WHERE S.業者番号 = SG.業者番号 -- 外部キー業者番号の対応付け --
AND SG.商品番号 = G.商品番号 -- 外部キー商品番号の対応付け --
// 上記の処理をC言語で書いたら
struct Table_G {
char 商品番号[ 6 ] ;
char 商品名[ 22 ] ;
char 色[ 4 ] ;
int 価格 ;
char 所在[ 12 ] ;
} = G[] = {
{ "G1" , "赤鉛筆" , "青" , 120 , "福井" } ,
:
} ;
// [結合] S,G,SGのすべての組み合わせ
// FROM S -- 結合
for( int i = 0 ; i < sizeofarray( S ) ; i++ ) {
// FROM G -- 結合
for( int j = 0 ; j < sizeofarray( G ) ; j++ ) {
// FROM SG -- 結合
for( int k = 0 ; k < sizeofarray( SG ) ; k++ ) {
// [選択] 条件でレコードを選び出す
// WHERE S.業者番号 = SG.業者番号
// AND SG.商品番号 = G.商品番号
if ( strcmp( S[i].業者番号 , SG[k].業者番号 ) == 0
&& strcmp( SG[k].商品番号 , G[j].商品番号 ) == 0 ) {
// [射影] 使用するフィールドを出力
printf( "%s %s %d\n" ,
S[i].業者名 , G[j].商品名 , SG[k].在庫量 ) ;
}
}
}
}
- 実験環境で結合/3つのTABLEの串刺し(学内のみ)
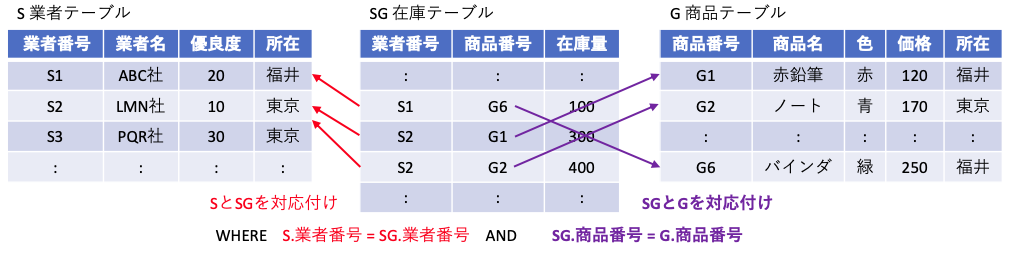 ここで結合と選択で実行している内容は、外部キーである業者番号を S から探す、商品番号を G から探している。この、外部キー対応しているものを探すという視点で、上記 C 言語のプログラムを書き換えると、以下のように表せる。
ここで結合と選択で実行している内容は、外部キーである業者番号を S から探す、商品番号を G から探している。この、外部キー対応しているものを探すという視点で、上記 C 言語のプログラムを書き換えると、以下のように表せる。
// FROM SG
for( int k = 0 ; k < sizeofarray( SG ) ; k++ ) {
// 外部キー SG.業者番号に対応するものを S から探す
for( int i = 0 ; i < sizeofarray( S ) ; i++ ) {
if ( strcmp( S[i].業者番号 , SG[k].業者番号 ) == 0 ) {
// 外部キー SG.商品番号に対応するものを G から探す
for( int j = 0 ; j < sizeofarray( G ) ; j++ ) {
if ( strcmp(SG[k].商品番号,G[j].商品番号) == 0 ) {
printf( "%s %s %d\n" ,
S[i].業者名,G[j].商品名,SG[k].在庫量 ) ;
}
}
}
}
}
このような、複数の表の実体と関係を対応付けた検索を、データベースの専門の人は「データを串刺しにする」という言い方をすることも多い。
また、SQL では、このようなイメージの繰り返し処理を、数行で分かりやすく記述できている。このプログラム例では、キーに対応するものを単純 for ループで説明しているが、SQL ではプライマリキーなら、B木やハッシュなどを用いた検索が行われるが、SQLの記述するときにはあまり考えなくて良い。
CTFのためのLinuxメモ
- WSL2 のインストール
- Linux環境を使う場合が多いので、WSL2(Windows Subsystem for Linux)をインストールしておきましょう。
ファイル関連
- データ形式 encode / decode
- MIME – メールで、テキストを文字コードを考慮して変換
- base64 – バイナリファイルの変換
- URL encode – WebアクセスでURLに情報を埋め込む
- file – ファイルの種別判断
- zip, unzip, gzip, gunzip – ファイルの圧縮解凍コマンド
- strings – ファイルの中の文字として読める部分の抽出
- more, less, lv – ページャ(ファイルビューア)
- grep – 指定した特定パターンの行だけ出力
- パイプ
- hexcurse – バイナリエディタ
- 4EI学生によると VSCode のプラグインで同等のものがあるらしい。
- big endian, little endian, network byte order
ネットワーク関連
- telnet – 特定のIPアドレス, ポートに接続して通信
- nc – telnet より特化したもの
- nslookup – DNS情報の参照
- dig – nslookup をより汎用にしたもの
- traceroute – ネットワーク経路
- ping – ネットワーク死活確認
- テキストブラウザ
- wget – どちらかというと、ダウンローダ?
- w3m – テキストブラウザ
- curl – 様々なプロトコルで通信できる。
- wireshark – パケットキャプチャ
OS関連
- gdb – デバッガ
- nm – オブジェクトファイルのシンボル情報出力
- objdump – 逆アセンブラ