ホーム » 2020
年別アーカイブ: 2020
sizeof(long int)
C言語のプログラミングで、型によってどの程度の数を記憶できるのかを説明することが多い。
注意して欲しい点としては、int型(32bit) = -231〜0〜231-1のあと、64bit を扱う場合はどう宣言するか。
今までは、long int は 実装により 32bit かもしれないし、64bit かもしれないので、64bit を使いたい場合は「gcc なら long long int 型を使って…」と説明していた。
しかし、説明資料を作っていたら、long int=32bit と思っていたけど、64bitだった。
改めて、最近の状況を確認したら、
- OSが “x86” なら long int = 32bit , long long int = 64bit
- OSが “x86_64” なら long int = 64bit , long long int = 64bit
なのね。
size_t 型
ちなみに、C言語では、malloc( ) に渡すメモリサイズなどは、2GB(231)を超える場合も想定する必要がある。このため、int で不具合が出る場合/出ない場合でプログラムを書き換えることがないように、size_t 型が定義されている。
実際には、以下のような typedef が #include <stdio.h>などの中で宣言されている。
((32bit)) typedef int size_t ; ((64bit)) typedef long long int size_t ;
ハッシュ法
ここまでの授業では、配列(データ検索は、登録順保存ならO(N)、2分探索ならO(log N)となる)、単純リスト(データ検索(シーケンシャルアクセスしかできないのでO(N)となる)、2分探索木( O(log N) ) といった手法を説明してきた。しかし、もっと高速なデータ検索はできないのであろうか?
究極のシンプルなやり方(メモリの無駄)
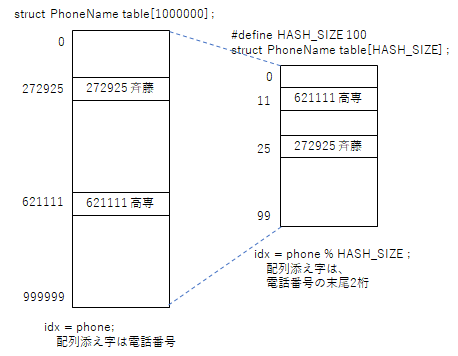
最も簡単なアルゴリズムは、電話番号から名前を求めるようなデータベースであれば、電話番号自身を配列添え字番号とする方法がある。しかしながら、この方法は大量のメモリを必要とする。
// メモリ無駄遣いな超高速方法
struct PhoneName {
int phone ;
char name[ 20 ] ;
} ;
// 電話番号は6桁とする。
struct PhoneName table[ 1000000 ] ; // 携帯電話番号ならどーなる!?!?
// 配列に電話番号と名前を保存
void entry( int phone , char* name ) {
table[ phone ].phone = phone ;
strcpy( table[ phone ].name , name ) ;
}
// 電話番号から名前を調べる
char* search( int phone ) {
return table[ phone ].name ;
}
しかし、50人程度のデータであれば、電話番号の末尾2桁を取り出した場合、同じ数値の人がいることは少ないであろう。であれば、電話番号の末尾2桁の値を配列の添え字番号として、データを保存すれば、配列サイズは100件となり、メモリの無駄を減らすことができる。
ハッシュ法
先に述べたように、データの一部を取り出して、それを配列の添え字番号として保存することで、高速にデータを読み書きできるようにするアルゴリズムはハッシュ法と呼ばれる。データを格納する表をハッシュ表、データの一部を取り出した添え字番号はハッシュ値、ハッシュ値を得るための関数がハッシュ関数と呼ばれる。
// ハッシュ衝突を考えないハッシュ法
#define HASH_SIZE 100 ;
struct PhoneName table[ HASH_SIZE ] ;
// ハッシュ関数
int hash_func( int phone ) {
return phone % HASH_SIZE ;
}
// 配列に電話番号と名前を保存
void entry( int phone , name ) {
int idx = hash_func( phone ) ;
table[ idx ].phone = phone ;
strcpy( table[ idx ].name , name ) ;
}
// 電話番号から名前を調べる
char* search( int phone ) {
int idx = hash_func( phone ) ;
return table[ idx ].name ;
}
ただし、上記のプログラムでは、電話番号の末尾2桁が偶然他の人と同じになることを考慮していない。
例えば、データ件数が100件あれば、同じ値の人も出てくるであろう。このように、異なるデータなのに同じハッシュ値が求まることを、ハッシュ衝突と呼ぶ。
たとえ話で言うなら、100個の椅子が連番付きで並んでいて、自分の電話番号末尾2桁の場所に座ろうとしたら、先に座っている人がいるような状態である。このような状態で、あなたなら何処に座るだろうか?
ハッシュ関数に求められる特性
ハッシュ関数は、できる限り同じような値が求まるものは、ハッシュ衝突が多発するので、避けなければならない。例えば、6桁の電話番号の先頭2桁であれば、電話番号の局番であり、同じ学校の人でデータを覚えたら、同じ地域の人でハッシュ衝突が発生してしまう。また、ハッシュ値を計算するのに、配列の空き場所を一つ一つ探すような方式では、データ件数に比例した時間がかかり、高速なアルゴリズムでなくなってしまう。このことから、ハッシュ関数には以下のような特徴が必要となる。
- 同じハッシュ値が発生しづらい(一見してデタラメのように見える値)
- 簡単な計算で求まること。
- 同じデータに対し常に、同じハッシュ値が求まること。
オープンアドレス法
先の椅子取りゲームの例え話であれば、先に座っている人がいた場合、最も簡単な椅子に座る方法は、隣が空いているか確認して空いていたらそこに座ればいい。
これをプログラムにしてみると、以下のようになる。このハッシュ法は、求まったアドレスの場所にこだわらない方式でオープンアドレス法と呼ばれる。
// オープンアドレス法
// table[] は大域変数で0で初期化されているものとする。
// 配列に電話番号と名前を保存
void entry( int phone , name ) {
int idx = hash_func( phone ) ;
while( table[ idx ].phone != 0 )
idx = (idx + 1) % HASH_SIZE ; // ひとつ後ろの席
} // idx++ でないのは何故?
table[ idx ].phone = phone ;
strcpy( table[ idx ].name , name ) ;
}
// 電話番号から名前を調べる
char* search( int phone ) {
int idx = hash_func( phone ) ;
while( table[ idx ].phone != 0 ) {
if ( table[ idx ].phone == phone )
return table[ idx ].name ;
idx = (idx + 1) % HASH_SIZE ; // ひとつ後ろの席
} // idx++ でないのは何故?
return NULL ; // 見つからなかった
}
注意:このプログラムは、ハッシュ表すべてにデータが埋まった場合、無限ループとなるので、実際にはもう少し改良が必要である。
この実装方法であれば、ハッシュ表にデータが少ない場合は、ハッシュ値を計算すれば終わり。よって、処理時間のオーダはO(1)となる。しかし、ハッシュ表がほぼ埋まっている状態だと、残りわずかな空き場所を探すようなもの。
チェイン法
前に述べたオープンアドレス法は、ハッシュ衝突が発生した場合、別のハッシュ値を求めそこに格納する。配列で実装した場合であれば、ハッシュ表のサイズ以上の データ件数を保存することはできない。
チェイン法は、同じハッシュ値のデータをグループ化して保存する方法。 同じハッシュ値のデータは、リスト構造とするのが一般的。
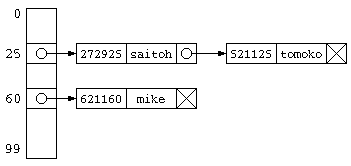
この処理にかかる時間は、データ件数が少なければ、O(1) となる。しかし、ハッシュ表のサイズよりかなり多いデータ件数が保存されているのであれば、ハッシュ表の先に平均「N/ハッシュ表サイズ」件のデータがリスト構造で並んでいることになるので、O(N) となってしまう。
#define SIZE 100
int hash_func( int ph ) {
return ph % SIZE ;
}
struct PhoneNameList {
int phone ;
char name[ 20 ] ;
struct PhoneNameList* next ;
} ;
struct PhoneNameList* hash[ SIZE ] ; // NULLで初期化
struct PhoneNameList* cons( int ph ,
char* nm ,
struct PhoneNameList* nx ) {
struct PhoneNameList* ans ;
ans = (struct PhoneNameList*)malloc(
sizeof( struct PhoneNameList ) ) ;
if ( ans != NULL ) {
ans->phone = ph ;
strcpy( ans->name , nm ) ;
ans->next = nx ;
}
return ans ;
}
void entry( int phone , char* name ) {
int idx = hash_func( phone ) ;
hash[ idx ] = cons( phone , name , hash[ idx ] ) ;
}
char* search( int phone ) {
int idx = hash_func( phone ) ;
struct PhoneNameList* p ;
for( p = hash[ idx ] ; p != NULL ; p = p->next ) {
if ( p->phone == phone )
return p->name ;
}
return NULL ;
}
文字列のハッシュ値
ここまでで説明した事例は、電話番号をキーとするものであり、余りを求めるだけといったような簡単な計算で、ハッシュ値が求められた。しかし、一般的には文字列といったような名前から、ハッシュ値が欲しいことが普通だろう。
ハッシュ値は、簡単な計算で、見た目デタラメな値が求まればいい。 (ただしく言えば、ハッシュ値の出現確率が極力一様であること)。一見規則性が解らない値として、文字であれば文字コードが考えられる。複数の文字で、これらの文字コードを加えるなどの計算をすれば、 偏りの少ない値を取り出すことができる。
int hash_func( char s[] ) {
int sum = 0 ;
for( int i = 0 ; s[i] != '¥0' ; i++ ) {
sum = sum + s[i] ;
}
return sum % SIZE ;
}
文字列順で異なる値となるように
前述のハッシュ関数は、”ABC”さんと”CBA”さんでは、同じハッシュ値が求まってしまう。文字列順で異なる値が求まるように改良してみる。
int hash_func( char s[] ) {
int sum = 0 ;
for( int i = 0 ; s[i] != '¥0' ; i++ ) {
sum = sum*2 + s[i] ;
// sum = (sum * 小さい素数 + s[i]) % 大きい素数 ;
}
return sum % SIZE ;
}
この後の授業の予定
- 共有のあるデータの取り扱い(参照カウンタ法,ガベージコレクタ) (1/14)
- 動的メモリ確保(malloc()とfreelist) (1/21)
- オブジェクト指向 (1/28)
- 予備 (2/4)
データベースの設計と正規形
データベースの設計において、重要な正規形についての説明
正規形
データベースにおいて、様々な不整合を防ぐために正しい設計が必要であることを 改めて説明し、それには正規形としての条件を満たしている必要があることを説明する。
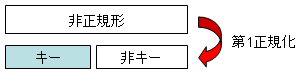
第一正規形は、すべての要素が原子値である条件を満たせばいい。 要素の中が複数の項目であったり表形式のデータがあると、 表構造のリレーショナルデータベースにはできない。
- 中央省庁のデータ表記を統一:河野太郎行政・規制改革担当相のTweet
データベースと直接関係しないけど、データは原子値じゃないと困るというお話。
キーの説明:超キー(スーパーキー)とは、データベースで1つのデータを 選び出すために必要なデータ項目であり、複数の項目で1データを指定 できる場合もある。
候補キーとは、必要最小限の項目となっているものを指す。 1項目が抜けても選別できなくなるようであれば、候補キーとは言わない。 主キーとは、候補キーのなかで管理の都合上便利なもの。
データ項目の値が決まると、他のデータ項目が自動的に決まるものは、 従属関係があるという。
 |
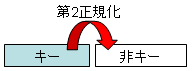 |
| 第1正規化 | 第2正規化 |
第二正規形は、部分従属がなく、すべての非キーデータ項目が、候補キーに 完全従属する場合をいう。
- 完全従属とは、候補キーを構成する全てのデータ項目に、非キーデータ項目が従属していること。
- 部分従属とは、候補キーを構成するデータ項目の一部のデータ項目に、非キー項目が従属していること。
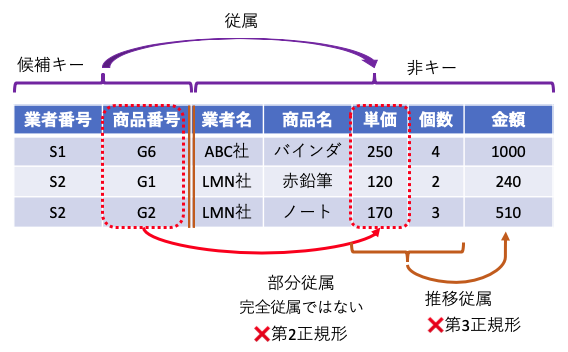 この例において、単価は商品が決まれば自動的に求まる情報。 (単価が日々変化することはないという条件で…) これは、部分従属となる。他に部分従属となっている属性は何か?
この例において、単価は商品が決まれば自動的に求まる情報。 (単価が日々変化することはないという条件で…) これは、部分従属となる。他に部分従属となっている属性は何か?
- 推移従属性とは、データ項目でA→B→Cと、次々と値が求められる関係を指す。
第三正規形とは、 候補キー以外の非キーデータ項目は、候補キーに完全従属し、 かつどの候補キーにも推移従属しない関係をいう。
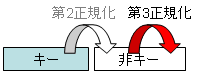 |
| 第3正規化 |
上記の例では、単価と個数が決まれば、金額が求まる推移従属の関係が含まれている。
おまけ:BC正規形,第4,5正規形
この他にも、 さらに非キーからキーに関数従属性がある場合にそれを取り除く、 ボイスコッド正規形(BC正規化)。 「対称性のある多値従属性(キーを決めると複数データが該当)」を分解して得られる第4正規形や、 「元になるテーブルの結合従属性を維持して分解することにより得られる第5正規形などがある。
トップダウン設計・ボトムアップ設計
データベースの設計にあたって、実際の設計手順の説明を行う。
トップダウン設計では、対象業務を記述し、その中から名詞となっている実体を抽出する。 さらに動詞や形容詞のように記載されている関連を抽出する。 抽出した実体・関連では、あいまいであったり冗長であったりするので、整理したうえで、 その実体・関連をER図に表す。
ボトムアップ設計では、対象業務で実際に使われている入力帳票や結果の出力などを 見ながら、第1正規形を満たすように表を作っていく作業からおこなう。
トップダウン設計やボトムアップ設計で、 ER図や第一正規形を満たすような表が出来上がったら、 その属性の中で従属性を確認しながら、第2正規形・第3正規形へと整理していく。
残りの授業の予定
- データベースの物理設計(1/13)
- トランザクション処理(1/20)
- B木とB+木とハッシュ法(1/27)
- 予備 (2/3)
CTF実験とobjdumpの使い方
CTF実験で、objdump を使う問題の解説。
元の問題は、https://tsaitoh.net/~t-saitoh/ctf/ の 問題6.1 use-the-strings 参照
機械語の知識が必要なCTF問題
use-the-strings の問題では、ダウンロードすると Linux 実行ファイルが得られる。
Linux の file コマンドでファイル種別を確認すると elf-x86-64 の実行ファイルであることがわかる。そこで、Linux の逆アセンブル命令でどのような命令か確認してみる。
$ file use-the-strings use-the-strings: ELF 64-bit LSB pie executable, x86-64, version 1 (SYSV)... $ sudo apt-get install binutils # binutilsはインストール済みかも $ objdump -d use-the-strings # use-the-stringsを逆アセンブル
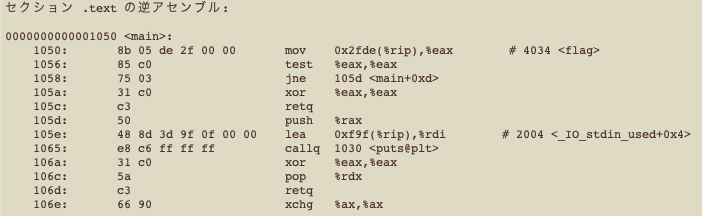
逆アセンブルにより出力されたプログラムの最も主要な部分を示す。
((2024/01/23追記))
サーバのOSのバージョンによっては、逆アセンブラ出力の関数の先頭に endbr64 という ”f3 0f 1e fa”の4byte命令が含まれているかもしれない。この命令が入っている場合は、この命令の分だけずれている。 endbr64 命令は、何らかの攻撃により不当な関数呼び出しがあった場合に強制的に終了させる命令らしい。
上記プログラムの機械語の逆アセンブラの結果を、C言語っぽく書くならば、以下のようになるだろう。
reg_eax = memory( 0x2fde+reg_rip ) ; // 大域変数flagを取り出す
if ( reg_eax != 0 ) goto label_105d ;
reg_eax = 0 ;
return ;
label_105d:
push( reg_rax ) ;
reg_rdi = 0xf9f+reg_rip ; // 出力文字の保存場所
puts() ; // 以下のputsを呼び出す。
reg_eax = 0 ;
pop( reg_rdx ) ;
return ;
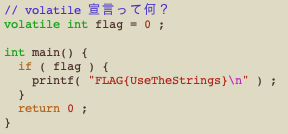
ちなみに、この use-the-strings の元プログラムは、以下のような内容である。
flag の変数に 0 以外の値が入っていれば、本来の出力処理が行われるはずだが、大域変数初期化にて通常であれば動かない。
このため printf を動かすには、以下の方法があるだろう。
- if 文(機械語ならば jne 命令の部分)を書き換えて、printf が実行されるようにする。
- if文を実行する前に、大域変数 flag を0以外の値に書き換える。
- 今回は、この方法の説明として、Cのソースプログラムとそのデバッガ情報を持った use-the-strings-gdb を使った方法を説明する。(ただし、Cのソースが手に入ったのなら答えもバレているはずだが…)
$ gdb use-the-strings-gdb GNU gdb (Debian 10.1-1+b1) 10.1 : (gdb) break main # ブレークポイントを設定 Breakpoint 1 at 0x1050: file use-the-strings.c, line 33. (gdb) run # プログラムを動かす Starting program: /home/t-saitoh/public_html/ctf/use-the-strings-gdb Breakpoint 1, main () at use-the-strings.c:33 33 if ( flag ) { # main() の先頭で一時停止 (gdb) set flag=1 # 変数 flag に 1 を代入 (gdb) continue # 続きを実行させる Continuing. FLAG{UseTheStrings} # 答えが表示された。 [Inferior 1 (process 767940) exited normally] (gdb) quit # デバッガを抜ける - gdb用のバイナリなしでも、gdbでプログラム動かせるな。
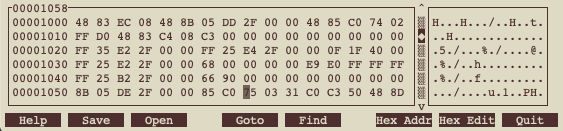
下記のように、gdb を起動して break main, run の状態で disassemble main を実行すると、参照しているメモリ(flag)が 0x555555558034 番地であることが確認できる。指定番地の内容参照の * を先頭につけて、set *0x555555558034=1 を実行すれば、flag に 1 を代入できる。$ gdb use-the-strings # デバッガの起動 (gdb) break main # mainにブレークポイントを設定 (gdb) run # ブレークポイントまで実行 (gdb) disassemble main # main以降を逆アセンブル (gdb) set *0x555555558034=1 # 逆アセンブル結果に記載された0x555555558034番地に1を書き込む (gdb) continue # 継続実行
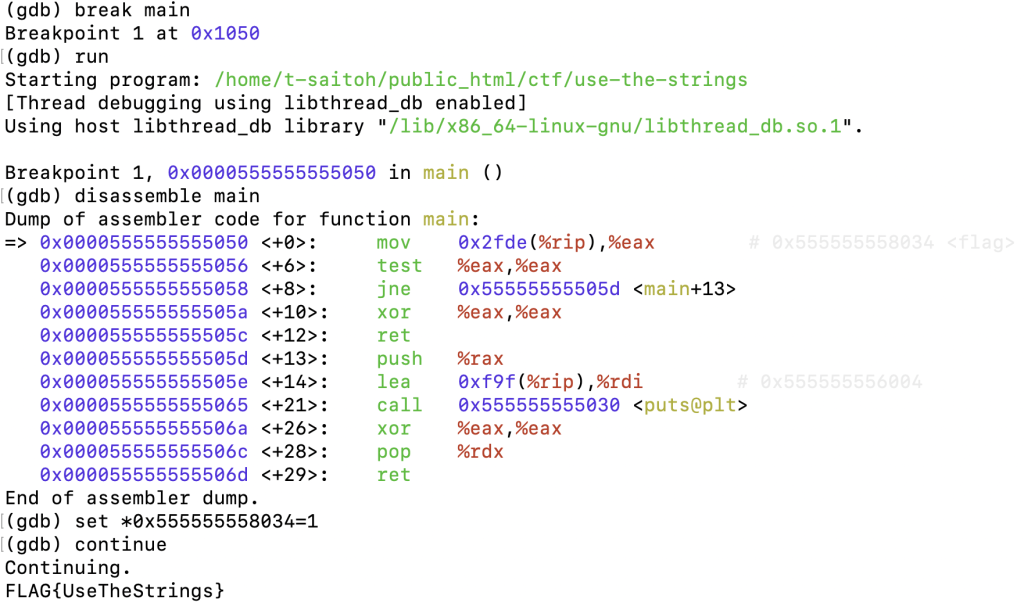
そもそももっと簡単な方法がある
機械語の知識に興味を持ってもらうために、あえて、上記のような説明をしたけど、本来はもっと簡単な手法がある。
strings コマンドは、ファイル中の英数字などで表示可能な文字部分を抽出して表示する。
$ strings use-the-strings
/lib64/ld-linux-x86-64.so.2
libc.so.6
puts
:
$ strings use-the-strings | grep FLAG # FLAGという文字を含むのが解っていれば
FLAG{UseTheStrings}
strings コマンドを使えばこの問題は極めて簡単に解けるが、ではCTFの難易度を高めるにはどうすればいいだろうか?
一般的に、ウィルス対策ソフトは、プログラム中の特定の機械語が、既知のウィルスの機械語パターンと一致しているかどうかで、ウィルスが含まれているか検知する。つまり、strings でバレない対策を考える…ということは、ウィルス作者が「如何にウィルス対策ソフトに見つからないウィルスを作るのか」ということに繋がる。
B木とデータベース
2分探索木の考え方を拡張したもので、B木がある。
B木の構造
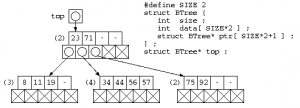
2分木では、データの増減で木の組換えの発生頻度が高い。そこで、1つのノード内に複数のデータを一定数覚える方法をとる。B木では、位数=Nに対し、最大2N個のデータd0..d2N-1と、2N+1本のポインタp0..p2Nから構成される。piの先には、di-1<x<di を満たすデータが入った B木のノードを配置する。ただし、データの充填率を下げないようにするため、データは最小でもN個、最大で2N個を保存する。
B木からデータの検索
データを探す場合は、ノード内のデータ diの中から探し、見つからない場合は、ポインタの先のデータを探す。位数がある程度大きい場合、ノード内の検索は2分探索法が使用できる。また、1つのノード内の検索が終われば、探索するデータ件数は、1/N〜1/2Nとなることから、指数的に対象件数が減っていく。よって、検索時間のオーダは、O(logN) となる。
B木へのデータの追加
B木にデータを追加する場合は、ノード内に空きがあれば、単純にデータの追加を行う。ノード内のデータが2N個を越える場合は、以下のような処理を行う。
ノード内のデータと追加データを並べ、その中央値を選ぶ。この中央値より大きいデータは、新たにつくられたノードに移す。中央値のデータは上のノードに追加処理を行う。このような方法を取ることで、2分木のような木の偏りが作られにくい構造となるようにする。
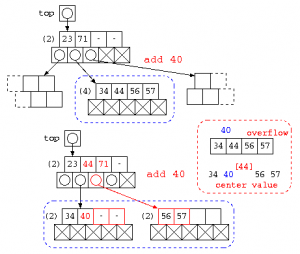
データを削除する場合も同様に、データ件数がN個を下回る場合は、隣接するノードからデータを取ってくることで、N個を下回らないようにする。
B木とデータベース
このB木の構造は、一般的にデータベースのデータを保存するために広く利用されている。
データベースシステムでは、データを効率よく保存するだけでなく、データの一貫性が保たれるように作られている。
例えば、データベースのシステムが途中でクラッシュした場合でも、データ更新履歴の情報を元にデータを元に戻し、データを再投入して復旧できなければならない。データを複数の所からアクセスした場合に、その順序から変な値にならないように、排他制御も行ってくれる。
データベースで最も使われているシステムは、データすべてを表形式で扱うリレーショナル・データベースである。
((リレーショナル・データベースの例)) STUDENT RESULT ID | name | grade | course ID | subject | point -----+----------+-------+-------- -----+---------+------- 1001 | t-saitoh | 5 | EI 1001 | math | 83 1002 | sakamoto | 4 | E 1001 | english | 65 1003 | aoyama | 4 | EI 1002 | english | 90 ((SQLの例)) select STUDENT.name, RESULT.subject, RESULT.point --射影-- from STUDENT , RESULT --結合-- where STUDENT.ID == RESULT.ID -- 串刺し -- --選択-- and RESULT.point >= 60 ; ((上記SQLをC言語で書いた場合)) for( st = 0 ; st < 3 ; st++ ) // 結合 for( re = 0 ; re < 3 ; re++ ) if ( student[ st ].ID == result[ re ].ID // 選択 && result[ re ].point >= 60 ) printf( "%s %s %d" , // 射影 student[ st ].name , result[ re ].subject , result[ re ].point ) ;
B+木
データベースの処理では、目的のデータを O(log N) で見つける以外にも、全データに対する処理も重要である。この場合、全てのデータに対する処理では、単純なB木では再帰呼び出しが必要となる。しかし、他の表でも再帰処理を伴うと、プログラムは複雑になってしまう。
そこで、B木のデータを横方向に並べて処理を行う場合に、その処理が簡単になるように B+木が用いられる。
この方法では、末端のノードは、隣接するノードへのポインタを持つ。

データベースの設計とER図
データベースの設計
リレーショナル・データベースでは、データは表形式であればなんでも良い訳ではない。
例えば、学生の成績データが以下のような構造であった場合、
ID | name | grade | subject | teacher ------+--------+-------+----------+--------- 20101 | aoyama | 1 | database | saitoh 20101 | aoyama | 1 | software | murata 20002 | suzuki | 2 | database | saitoh 20002 | suzuki | 2 | compiler | nomura 30203 | yamada | 3 | media | ogoshi
- 修正不整合: 授業担当が saitoh → sasaki のように変更になったら、複数のテーブルを修正しなければならない。大量のレコード修正は、時間がかかるし、その途中にシステムダウンしたらデータの整合性に問題が発生するかも。
- 挿入不整合: 新しい科目 internet を追加したいけど、受講学生が決まらないとデータを挿入できない。
- 削除不整合: yamada が受講を取りやめたら、科目 media も消えてしまう。
これらを考慮すると、以下のような3つの表で設計するべきである。
学生 受講 科目
ID | name | grade ID | SubID SubID | subject | teacher
------+--------+------- ------+------- ------+----------+--------
20101 | aoyama | 1 20101 | 1001 1001 | database | saitoh → sasaki
20002 | suzuki | 2 20101 | 1002 1002 | software | murata
30203 | yamada | 3 20002 | 1001 1003 | compiler | nomura
20002 | 1003 1004 | media | ogoshi
消す→ 30203 | 1004 1005 | internet | foobar → 追加
データベースの設計では、(1)概念設計、(2)論理設計、(3)物理設計が行われる。
- 概念設計:概念スキーマの決定(実体・関係モデルを使う)。上記の受講データベースの設計例
- 論理設計:論理スキーマの決定。関係データベースで実装?ほかのデータベース?
- 物理設計:物理スキーマの決定。データの格納方法や管理方法を決める。
実体関連モデル(ERモデル)
データベース設計では、実体関連モデル(ERモデル:Entity-Relation model)が使われる。 実体とは、モデル化しようとする対象で独立した存在となれるもの。 実体が持つ色々な特性は属性と呼ばれる。 属性の取りうる値の集合を定義域、同一種類の実体の集まりを実体集合と呼ぶ。 関連とは、実体同士の相互関係をモデル化したもの。
実体関連図(ER図)では、実体を長方形、関連をひし形、属性を楕円で表現する。 属性で、キーとなるものには下線をつけて表す。

ER図で調べると、実際にはもっと細かい規定で表現が行われている。 参考:IDEF1X表記とIE表記
デザコンAM部門に参加
今日は、高専のデザインコンテスト。
参加部門は3DプリンタのAMデザイン部門だけど、コロナでZoom開催です。例年盛り上がる「ぶっ壊れるまで」の構造デザイン部門はナシで、空間デザイン部門などが開催されています。
3Dプリンタを使ったデザインを提案するAMデザイン部門には、専攻科の創造デザイン演習の授業の中で取り組んだ3つの作品を応募し、その中で「補強にもおしゃれにも役立つネイルチップ」(専攻科1年,山本,西島,定兼,廣谷)が本戦参加となりました。
1日目のプレゼンテーション風景
本戦参加6チームのうち、当日朝のくじ引きで発表順は最後になりました。
2日目のディスカッション風景
2日目は、初日と逆順となり、最初にディスカッションとなりました。
基本アイデアについては、高く評価してもらえましたが、試作した3Dプリントで実現したいコンセプトの物を作ることができていなかったため、その点が残念だったとの講評をいただきました。
CTF実験: unix 系開発環境のインストール
CTFでは、様々な unix 系の開発環境のコマンドが用いられる。
これらの環境を構築するためのメモを記載。
Windows の場合
macOS の場合
macOS で unix 系の開発環境を使う場合には、homebrew や MacPorts を用いることが多い。
CTFでよく使われるunix系パッケージ
((ファイル系))
file - ファイルの種別判定
zip - zip,unzip(ファイル圧縮解凍)
gzip - gzip,gunzip(ファイル圧縮解凍-GNU)
nkf - nkf(日本語漢字フィルタ)
hexcurse - hexcurse(バイナリエディタ)
((OS系))
gcc - gcc(コンパイラ-GNU)
gdb - gdb(デバッガ-GNU)
binutils - objdump(逆アセンブラ) ,
- nm(オブジェクトファイルのシンボル出力) ,
- strings(文字部分の出力)
((ネットワーク系))
telnet - telnet(telnetクライアント)
netcat-openbsd - nc(TCP/IP 汎用ツール)
bind9-dnsutils - nslookup, dig(DNS参照ツール)
whois - whois(ディレクトリサービスクライアント)
((ブラウザ系))
w3m - w3m(テキストブラウザ)
wget - wget(テキストブラウザ+ダウンローダ)
curl - curl(ダウンローダ)
((使用上要注意))
nmap - nmap(ネットワーク調査ツール)
wireshark - wireshark(パケットキャプチャ)
- windows用とかmac用のバイナリの方が便利
各unix系のインストールコマンド
((WSL2の場合)) $ sudo apt-get install gcc binutils ((Homebrew の場合)) $ sudo brew install gcc binutils ((MacPorts の場合)) $ sudo port install gcc binutils