リスト構造は、必要に応じてメモリを確保するデータ構造であり、データ件数に依存しないプログラム が記述できる。その応用として、集合処理を考えてみる。集合処理の記述には、2進数を使った方式やリストを用いた方法が一般的である。以下にその処理について示す。
bit演算子
2進数を用いた集合処理を説明する前に、2進数を使った計算に必要なbit演算子について復習してみる。
bit演算子は、その数値を2進数表記とした時の各ビットをそれぞれAND,OR,EXOR,NOTなどの計算を行う。
| bit演算子 | 計算の意味 | 関連知識 |
|---|---|---|
| & bit AND | 3 & 5 0011)2 & 0101)2= 0001)2 |
論理積演算子 if ( a == 1 && b == 2 ) … |
| | bit OR | 3 | 5 0011)2 | 0101)2= 0111)2 |
論理和演算子 if ( a == 1 || b == 2 ) … |
| ~ bit NOT | ~5 ~ 00..00,0101)2= 11..11,1010)2 |
論理否定演算子 if ( !a == 1 ) … |
| ^ bit EXOR | 3 ^ 5 0011)2 ^ 0101)2= 0110)2 |
|
| << bit 左シフト | 3 << 2 0011)2 << 2 = 001100)2 |
x << y は |
| >> bit 右シフト | 12 >> 2 1100)2 >> 2 = 11)2 |
x >> y は |
import java.util.*;
public class Main {
public static void main(String[] args) throws Exception {
System.out.println( 12 & 5 ) ; // 1100 & 0101 = 0100 = 4
System.out.println( 12 | 5 ) ; // 1100 | 0101 = 1101 = 13
System.out.println( ~12 & 0xF ) ; // ~1100 & 1111 = 0011 = 3
System.out.println( 3 << 2 ) ; // 0011 << 2 = 1100
System.out.println( 12 >> 2 ) ; // 1100 >> 2 = 0011
System.out.println( ~12 + 1 ) ; // ~0..00001100 + 1 = 1..11110011 + 1 = 1..11110100 = -12
}
}
論理演算子とbit演算子の違い
論理積,論理和という点では、論理演算子&&,|| と bit演算子&,| は複数桁の2進数で計算する違いと思うかもしれないが、論理演算子&&,|| は若干挙動が違う。論理積&&演算子は、左辺の結果が false だと(結果がfalse確定なので) 右辺の計算式や呼び出されない。同じように論理和||演算子は、左辺の結果が true だと(結果がtrue確定なので) 右辺の計算式は呼び出されない。
import java.util.*; public class Main { static boolean boolean_print( boolean yn ) { System.out.print( yn + " " ) ; return yn ; } static int int_print( int yn ) { System.out.print( yn + " " ) ; return yn ; } public static void main(String[] args) throws Exception { boolean ans ; int x ; ans = boolean_print( true ) && boolean_print( true ) ; System.out.println() ; ans = boolean_print( false ) && boolean_print( true ) ; System.out.println() ; ans = boolean_print( true ) || boolean_print( true ) ; System.out.println() ; ans = boolean_print( false ) || boolean_print( true ) ; System.out.println() ; x = int_print( 0 ) & int_print( 1 ) ; System.out.println() ; x = int_print( 1 ) | int_print( 0 ) ; System.out.println() ; } }
- 論理演算子とbit演算子の違い(Paiza.io)
2進数とビットフィールド
例えば、誕生日の年月日の情報を扱う際、20230726で、2023年7月26日を表現することも多い。
しかしこの方法は、この年月日の情報から年(4桁)、月(2桁)、日(2桁)を取り出す処理では、乗算除算が必要となる。通常のCPUであれば、簡単な乗除算は速度的にも問題はないが、組込み系では処理速度の低下も懸念される。
int ymd = 20230726 ; int y , m , d ; y = ymd / 10000 ; m = ymd / 100 % 100 ; d = ymd % 100 ; y = 1965 ; m = 2 ; d = 7 ; ymd = y * 10000 + m * 100 + d ;
こういった処理を扱う際には、2進数の考え方を使って扱う方法がある。
例えば、年は 0..2047 の範囲と考えれば 11 bit で表現でき、月は1..12の範囲であり 4bit で表現可能であり、日は1..31 で 5bit で表現できる。これを踏まえて、年月日を 11+4+5 = 20bit で表す(YYYY,YYYY,YYYM,MMMD,DDDD)なら、以下のプログラムのように書ける。
int ymd = (2024 << 9) + (7 << 5) + 26 ; // YYYY,YYYY,YYYM,MMMD,DDDD int y , m , d ; // 1111,1101,0000,1111,1010 y = ymd >> 9 ; // YYYYYYYYYYY m = (ymd >> 5) & 0xF ; // YYYYYYYYYYYMMMM & 000000000001111 d = (ymd & 0x1F) ; // YYYYYYYYYYYMMMMDDDDD & 00000000000000011111 y = 1965 ; m = 2 ; d = 7 ; ymd = (y << 9) + (m << 5) + d ;
C言語でのビットフィールド
しかし、上記のプログラムでは、いちいち2進数bit演算をイメージする必要があって、プログラムが分かりづらい。C言語では、こういった際にに使うのが ビットフィールドである。
// C言語の場合 (Javaではビットフィールドの構文がない) struct YMD { unsigned int year : 11 ; // ビットフィールドでは、 unsigned int month : 4 ; // 構造体の要素を何ビットで保存するのか unsigned int day : 5 ; // 指定することができる。 } ; struct YMD ymd = { 2023 , 7 , 26 } ; int y , m , d ; y = ymd.year ; m = ymd.month ; d = ymd.day ; ymd.year = 1965 ; ymd.month = 2 ; ymd.day = 7 ;
2進数を用いた集合計算
リストによる集合の前に、もっと簡単な集合処理を考える。
最も簡単な方法は、要素に含まれる=true か 含まれない=false を boolean型の配列に覚える方法であろう。数字Nが集合に含まれる場合は、配列[N]に true を覚えるものとする。この方法で積集合などを記述した例を以下に示す。
import java.util.*;
public class Main {
public static void boolarray_print( boolean[] a ) {
for( int i = 0 ; i < a.length ; i++ )
System.out.print( a[i] ? "T" : "F" ) ;
System.out.println() ;
}
public static void boolarray_and( boolean[] ans , boolean[] a , boolean[] b ) {
for( int i = 0 ; i < a.length ; i++ )
ans[i] = a[i] && b[i] ;
}
public static void boolarray_or( boolean[] ans , boolean[] a , boolean[] b ) {
for( int i = 0 ; i < a.length ; i++ )
ans[i] = a[i] || b[i] ;
}
public static void main(String[] args) throws Exception {
// 0 1 2 3 4 5 6 7 8 9
boolean[] ba = { false, true, true, true, false, false, false, false, false, false } ; // {1,2,3}
boolean[] bb = { false, false, true, false, true, false, true, false, false, false } ; // {2,4,6}
boolean[] bc = { false, false, false, false, true, false, true, false, false, true } ; // {4,6,9}
boolean[] ans = new boolean[ 10 ] ;
boolarray_print( ba ) ;
boolarray_print( bb ) ;
boolarray_and( ans , ba , bb ) ;
boolarray_print( ans ) ;
boolarray_print( bb ) ;
boolarray_print( bc ) ;
boolarray_or( ans , bb , bc ) ;
boolarray_print( ans ) ;
}
}
FTTTFFFFFF // ba
FFTFTFTFFF // bb
FFTFFFFFFF // ba & bb
FFTFTFTFFF // bb
FFFFTFTFFT // bc
FFTFTFTFFT // bb | bc
しかし、上述のプログラムでは、要素に含まれる/含まれないという1bitの情報をboolean型で保存しているが、実体は整数型で保存しているためメモリの無駄となる。
データ件数の上限が少ない場合には、「2進数の列」の各ビットを集合の各要素に対応づけし、要素の有無を0/1で表現する。この方法を用いるとビット演算命令で 和集合、積集合を計算できるので、処理が極めて簡単になる。
2進数を用いた集合計算
扱うデータ件数が少ない場合には、「2進数の列」の各ビットを集合の各要素に対応づけし、要素の有無を0/1で表現する。この方法を用いるとC言語のビット演算命令で 和集合、積集合を計算できるので、処理が極めて簡単になる。
以下のプログラムは、0〜31の数字を2進数の各ビットに対応付けし、 ba = {1,2,3} , bb = {2,4,6} , bc= {4,6,9} を要素として持つ集合で、ba ∩ bb , bb ∪ bc の計算を行う例である。
import java.util.*;
public class Main {
static void bitfield_print( int x ) {
for( int i = 0 ; i < 10 ; i++ )
System.out.print( ((x & (1 << i)) != 0) ? "T" : "F" ) ;
System.out.println() ;
}
public static void main(String[] args) throws Exception {
int ba = (1 << 1) | (1 << 2) | (1 << 3) ; // {1,2,3}
int bb = (1 << 2) | (1 << 4) | (1 << 6) ; // {2,4,6}
int bc = (1 << 4) | (1 << 6) | (1 << 9) ; // {4,6,9}
bitfield_print( ba ) ;
bitfield_print( bb ) ;
bitfield_print( ba & bb ) ;
bitfield_print( bb ) ;
bitfield_print( bc ) ;
bitfield_print( bb | bc ) ;
}
}
有名なものとして、エラトステネスのふるいによる素数計算を2進数を用いて記述してみる。このアルゴリズムでは、各bitを整数に対応付けし、素数で無いと判断した2進数の各桁に1の目印をつけていく方式である。
import java.util.*;
public class Main {
static final int INT_BITS = 31 ;
static int prime = 0 ;
public static void main(String[] args) throws Exception {
// 倍数に非素数の目印をつける
for( int i = 2 ; i <= INT_BITS ; i++ ) {
if ( (prime & (1 << i)) == 0 ) {
for( int j = 2 * i ; j <= INT_BITS ; j += i )
prime |= (1 << j) ;
}
}
// 非素数の目印の無い値を出力
for( int i = 2 ; i <= INT_BITS ; i++ ) {
// 目印のついていない値は素数
if ( (prime & (1 << i)) == 0 )
System.out.println( i ) ;
}
}
}
リスト処理による積集合
前述の方法は、リストに含まれる/含まれないを、2進数の0/1で表現する方式である。しかし、2進数であれば、int で 31要素、long int で 63 要素が上限となってしまう。
しかし、リスト構造であれば、リストの要素として扱うことで、要素件数は自由に扱える。また、今までの授業で説明してきた cons() などを使って表現すれば、簡単なプログラムでリストの処理が記述できる。
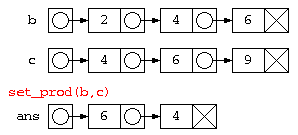
例えば、積集合(a ∩ b)を求めるのであれば、リストa の各要素が、リストb の中に含まれるか find 関数でチェックし、 両方に含まれたものだけを、ans に加えていく…という考えでプログラムを作ると以下のようになる。
import java.util.*;
class ListNode {
int data ;
ListNode next ;
ListNode( int d , ListNode n ) {
this.data = d ;
this.next = n ;
}
static void print( ListNode p ) {
for( ; p != null ; p = p.next )
System.out.print( p.data + " " ) ;
System.out.println() ;
}
static boolean find( ListNode p , int key ) {
for( ; p != null ; p = p.next )
if ( p.data == key )
return true ;
return false ;
}
static ListNode set_prod( ListNode a , ListNode b ) {
ListNode ans = null ;
for( ; a != null ; a = a.next ) {
if ( find( b , a.data ) )
ans = new ListNode( a.data , ans ) ;
}
return ans ;
}
} ;
public class Main {
public static void main(String[] args) throws Exception {
ListNode b = new ListNode( 2 , new ListNode( 4 , new ListNode( 6 , null ) ) ) ;
ListNode c = new ListNode( 4 , new ListNode( 6 , new ListNode( 9 , null ) ) ) ;
ListNode b_and_c = ListNode.set_prod( b , c ) ;
ListNode.print( b_and_c ) ;
}
}
例題として、和集合、差集合などを考えてみよう。
理解確認
- 2進数を用いた集合処理は、どのように行うか?
- リスト構造を用いた集合処理は、どのように行うか?
- 積集合(A ∩ B)、和集合(A ∪ B)、差集合(A – B) の処理を記述せよ。