前回の授業では、リストの先頭にデータを挿入する処理と、末尾に追加する処理について説明したが、この応用について説明する。

計算処理中に一時的なデータの保存として、スタック(stack)と待ち行列・キュー(queue)がよく利用される。それを配列を使って記述したり、任意の大きさにできるリストを用いて記述することを示す。

スタック

配列を用いたスタック

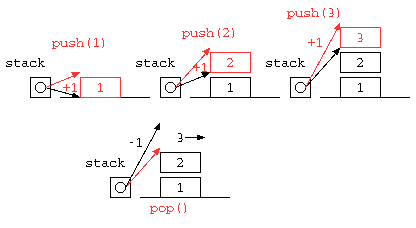
一時的な値の記憶によく利用されるスタック(stack)は、データの覚え方の特徴からLIFO( Last In First out )とも呼ばれる。配列を使って記述すると以下のようになるであろう。

import java.util.*;

public class Main {
    static final int STACK_SIZE = 10 ;
    static int[] stack = new int[ STACK_SIZE ] ;
    static int   sp    = 0 ;
    static void push( int x ) {
        stack[ sp++ ] = x ;
    }
    static int pop() {
        return stack[ --sp ] ;
    }
    public static void main(String[] args) throws Exception {
        push( 11 ) ;
        push( 22 ) ;
        push( 33 ) ;
        System.out.println( pop() ) ;
        System.out.println( pop() ) ;
        System.out.println( pop() ) ;
    }
}

配列を使った Stack をオブジェクト指向で記述するなら、以下のように書ける。

import java.util.*;

class Stack {
    static final int STACK_SIZE = 10 ;
    int[] array ;
    int   sp ;
    Stack() {
        this.array = new int[ STACK_SIZE ] ;
        this.sp    = 0 ;
    }
    void push( int x ) {
        array[ sp++ ] = x ;
    }
    int pop() {
        return array[ --sp ] ;
    }
} ;

public class Main {
    public static void main(String[] args) throws Exception {
        Stack stack = new Stack() ;
        stack.push( 11 ) ;
        stack.push( 22 ) ;
        stack.push( 33 ) ;
        System.out.println( stack.pop() ) ;
        System.out.println( stack.pop() ) ;
        System.out.println( stack.pop() ) ;
    }
}

C言語で書いた場合

#define STACK_SIZE 32
int stack[ STACK_SIZE ] ;
int sp = 0 ;

void push( int x ) { // データをスタックの一番上に積む
    stack[ sp++ ] = x ;
}
int pop() { // スタックの一番うえのデータを取り出す
    return stack[ --sp ] ;
}
void main() {
    push( 1 ) ; push( 2 ) ; push( 3 ) ;
    printf( "%d\n" , pop() ) ; // 3
    printf( "%d\n" , pop() ) ; // 2
    printf( "%d\n" , pop() ) ; // 1
}

++,–の前置型と後置型の違い

// 後置インクリメント演算子
int i = 100 ;
printf( "%d" , i++ ) ;
// これは、
printf( "%d" , i ) ;
i++ ;
// と同じ。100が表示された後、101になる。

// 前置インクリメント演算子
int i = 100 ;
printf( "%d" , ++i ) ;
//   これは、
i++ ;
printf( "%d" , i ) ;
// と同じ。101になった後、101を表示。

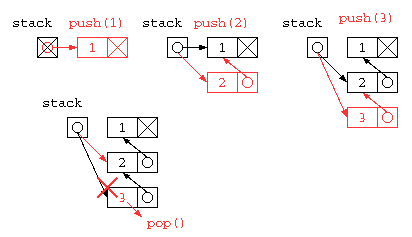
リスト構造を用いたスタック

しかし、この中にSTACK_SIZE以上のデータは貯えられない。同じ処理をリストを使って記述すれば、配列サイズの上限を気にすることなく使うことができるだろう。では、リスト構造を使ってスタックの処理を記述してみる。

import java.util.*;

class ListNode {
    int      data ;
    ListNode next ;
    ListNode( int d , ListNode n ) {
        this.data = d ;
        this.next = n ;
    }
}

public class Main {
    static ListNode stack = null ;
    static void push( int x ) {
        stack = new ListNode( x , stack ) ;
    }
    static int pop() {
        int ans = stack.data ;
        stack = stack.next ;
        return ans ;
    }
    public static void main(String[] args) throws Exception {
        push( 1 ) ;
        push( 2 ) ;
        push( 3 ) ;
        System.out.println( pop() ) ;
        System.out.println( pop() ) ;
        System.out.println( pop() ) ;
    }
}

struct List* stack = NULL ;

void push( int x ) { // リスト先頭に挿入
    stack = cons( x , stack ) ;
}
int pop() { // リスト先頭を取り出す
    int ans = stack->data ;
    struct List* d = stack ;
    stack = stack->next ;      // データ 0 件で pop() した場合のエラー対策は省略
    free( d ) ;
    return ans ;
}

オブジェクト指向っぽく書くならば、下記のようになるだろう。初期状態で stack = null にしておくと、stack.push() ができないので、stack の先頭には、ダミーデータを入れるようにプログラムを書くと以下のようになるだろう。

import java.util.*;

class ListNode {
    int      data ;
    ListNode next ;
    ListNode( int d , ListNode n ) {
        this.data = d ;
        this.next = n ;
    }
    ListNode() {   // stack初期化用のコンストラクタ
        this.data = -1 ;
        this.next = null ;
    }
    void push( int x ) {
        this.next = new ListNode( x , this.next ) ;
    }
    int pop() {
        int ans = this.next.data ;
        this.next = this.next.next ;
        return ans ;
    }
} ;

public class Main {
    public static void main(String[] args) throws Exception {
        ListNode stack = new ListNode() ; // stack初期化用のコンストラクタを使う
        stack.push( 1 ) ;
        stack.push( 2 ) ;
        System.out.println( stack.pop() ) ;
        System.out.println( stack.pop() ) ;
    }
}

キュー(QUEUE)

２つの処理の間でデータを受け渡す際に、その間に入って一時的にデータを蓄えるためには、待ち行列(キュー:queue)がよく利用される。 データの覚え方の特徴からFIFO(First In First Out)とも呼ばれる。

配列を用いたQUEUE / リングバッファ

配列にデータを入れる場所(wp)と取り出す場所のポインタ(rp)を使って蓄えれば良いが、配列サイズを超えることができないので、データを取り出したあとの場所を循環して用いるリングバッファは以下のようなコードで示される。

import java.util.*;

public class Main {
    static final int QUEUE_SIZE = 32 ;
    static int[] queue = new int[ QUEUE_SIZE ] ;
    static int wp = 0 ;
    static int rp = 0 ;
    static void put( int x ) {
        queue[ wp++ ] = x ;
        if ( wp >= QUEUE_SIZE ) // wp = wp % QUEUE_SIZE ; or wp = wp & (QUEUE_SIZE - 1) ;
            wp = 0 ;
    }
    static int get() {
        int ans = queue[ rp++ ] ;
        if ( rp >= QUEUE_SIZE ) // rp = rp % QUEUE_SIZE ; or rp = rp & (QUEUE_SIZE - 1) ;
            rp = 0 ;
        return ans ;
    }
    public static void main(String[] args) throws Exception {
        // Your code here!
        put( 1 ) ;
        put( 2 ) ;
        put( 3 ) ;
        System.out.println( get() ) ;
        System.out.println( get() ) ;
        System.out.println( get() ) ;
    }
}

#define QUEUE_SIZE 32
int queue[ QUEUE_SIZE ] ;
int wp = 0 ; // write pointer(書き込み用)
int rp = 0 ; // read  pointer(読み出し用)

void put( int x ) { // 書き込んで後ろ(次)に移動
    queue[ wp++ ] = x ;
    if ( wp >= QUEUE_SIZE )  // 末尾なら先頭に戻る
        wp = 0 ;
}
int get() { // 読み出して後ろ(次)に移動
    int ans = queue[ rp++ ] ;
    if ( rp >= QUEUE_SIZE )  // 末尾なら先頭に戻る
        rp = 0 ;
    return ans ;
}
void main() {
    put( 1 ) ; put( 2 ) ; put( 3 ) ;
    printf( "%d\n" , get() ) ; // 1
    printf( "%d\n" , get() ) ; // 2
    printf( "%d\n" , get() ) ; // 3
}

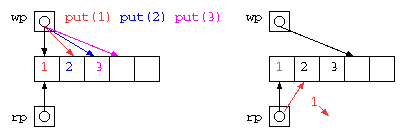
このようなデータ構造も、get() の実行が滞るようであれば、wp が rp に循環して追いついてしまう。このため、上記コードはまだエラー対策としては不十分である。どのようにすべきか？

 

リスト構造を用いたQUEUE

前述のリングバッファもget()しないまま、配列上限を越えてput()を続けることはできない。

この配列サイズの上限問題を解決したいのであれば、リスト構造を使って解決することもできる。この場合のプログラムは、以下のようになるだろう。

import java.util.*;

class ListNode {
   int      data ;
   ListNode next ;
   ListNode( int d , ListNode n ) {
       this.data = d ;
       this.next = n ;
   }
} ;

public class Main {
    static ListNode top = new ListNode( -1 , null ) ;
    static ListNode tail = top ;
    static void put( int x ) {
        tail.next = new ListNode( x , null ) ;
        tail = tail.next ;
    }
    static int get() {
        int ans = top.next.data ;
        top.next = top.next.next ;
        return ans ;
    }
    public static void main(String[] args) throws Exception {
        put( 1 ) ;
        put( 2 ) ;
        put( 3 ) ;
        System.out.println( get() ) ;
        System.out.println( get() ) ;
        System.out.println( get() ) ;
    }
}

Javaで書かれた ListNode を用いた待ち行列のイメージ図は下記のように示される。

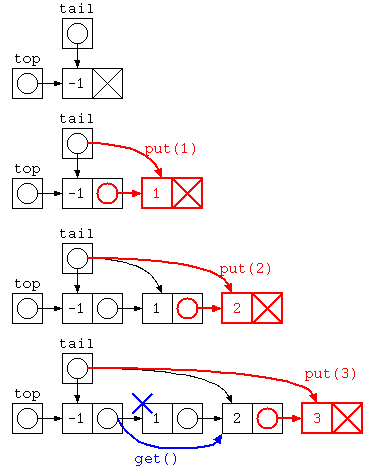
struct List* queue = NULL ;
struct List** tail = &queue ;

void put( int x ) { // リスト末尾に追加
    *tail = cons( x , NULL ) ;
    tail = &( (*tail)->next ) ;
}
int get() { // リスト先頭から取り出す
    int ans = queue->data ;
    struct List* d = queue ;
    queue = queue->next ;
    free( d ) ;
    return ans ;
}

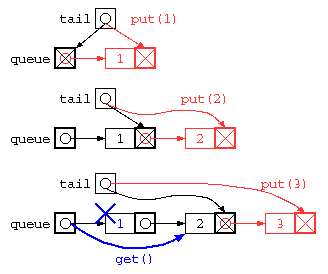
ただし、上記のプログラムは、データ格納後にget()で全データを取り出してしまうと、tail ポインタが正しい位置になっていないため、おかしな状態になってしまう。
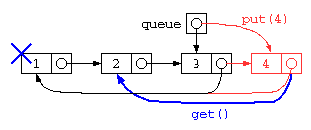
また、このプログラムでは、rp,wp の2つのポインタで管理することになるが、 2重管理を防ぐために、リストの先頭と末尾を1つのセルで管理する循環リストが使われることが多い。

理解確認

• 配列を用いたスタック・待ち行列は、どのような処理か？図などを用いて説明せよ。
• リスト構造を用いたスタック・待ち行列について、図などを用いて説明せよ。
• スタックや待ち行列を、配列でなくリスト構造を用いることで、どういう利点があるか？欠点があるか説明せよ。
• 配列を用いたリングバッファが用いられている身近な例にはどのようなものがあるか？
• 配列を用いたリングバッファを実装する場合配列サイズには 2ⁿ 個を用いることが多いのはなぜだろうか？