ライブラリと分割コンパイル
巨大なプログラムを作ってくると、プログラムのコンパイルに時間がかかる。こういった場合には、共有できる処理であればライブラリにまとめたり、分割コンパイルといった方法をとる。
C言語とライブラリ
C言語でプログラムを作っている時、printf() や scanf() といった関数を使うが、こういった組み込み関数のプログラムはどこに書かれているのだろうか?
ソースプログラムがコンパイルする際には、コンパイラ(compiler)によるコンパイル処理(compiler)、リンカ(linker or linkage editor)によるリンク処理(link)が行われる。この時に、printf()やscanf() の機械語(組み込み関数などのライブラリの内容)が実行プログラム a.out の中に埋め込まれる。通常は、コンパイルとリンク処理は一連の処理として実行される。
helloworld.c ソースプログラム ↓ compiler $ gcc -c helloworld.c (コンパイルだけ行う) ↓ ただしC言語では、コンパイルの前にプリプロセッサ処理 #include,#define の処理が行われる。 helloworld.o オブジェクトファイル(中間コード) ↓ linker $ gcc helloworld.o (リンク処理を行う) (+) ← libgcc.a ライブラリ(printf, scanf....) ↓ $ ./a.out a.out 実行プログラム
静的リンクライブラリと動的リンクライブラリ
しかし、printf() や scanf() のような組み込み関数の機械語が実行プログラムの中に単純に埋め込まれると、
- よく使われるprintf()やscanf()の処理は、沢山の実行プログラムの中に埋め込まれる。
そして、組み込み関数を使ったプログラムが複数実行されると、実行中のメモリに複数の組み込み関数の処理が配置されてメモリの無駄が発生する。 - その組み込み関数に間違いがあった場合、その組み込み関数を使った実行プログラムをすべて再コンパイルしないといけなくなる。
リンクされたプログラムの機械語が実行プログラムに埋め込まれる方式は、静的リンクライブラリと呼ぶ。
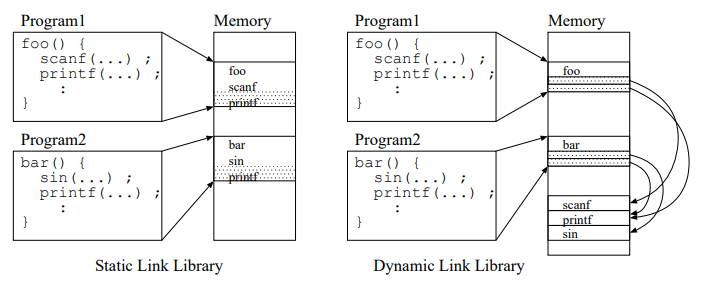
しかし、静的リンクライブラリの方式は、実行時の命令の領域のムダや、ライブラリに間違いがあった場合の再コンパイルの手間があるため、動的リンクライブラリ方式(共有ライブラリ方式)がとられる。
動的リンクライブラリでは、プログラム内には動的リンクを参照するための必要最小限の命令が埋め込まれ、命令の実体は OS が動的リンクライブラリとして管理する。
Linux では、静的リンクライブラリのファイルは、lib~.a といった名前で保存され、動的リンクライブラリは、lib~.so という名前で保存されている。 Windows であれば、拡張子が ~.DLL のファイルが動的リンクライブラリである。
OS にとって必須の動的リンクライブラリは /lib 配下に保存されるが、ユーザが独自にインストールするパッケージの場合 /lib のアクセス権限の都合で別の場所に保存されるかもしれない。この場合、その独自パッケージを起動する時に、動的リンクライブラリの保存場所を見つけ出す必要がある。Linux では 環境変数 LD_LIBRARY_PATH に自分が利用する動的リンクライブラリの保存場所を記載すれば、OS がプログラム起動時に動的リンクライブラリを見つけてくれる。
Javaのコンパイル と JIT と CLASSPATH
Java のプログラムを実行する場合は、以下のような流れで実行される。
Main.java ソースプログラム ↓ コンパイラ $ javac Main.java Main.class Javaバイトコード ↓ JVM実行 $ java Main (Main.classを実行) JIT (Just In Time コンパイラ) ↓ バイトコードを機械語に変換 機械語を実行
この場合、複数のファイルに分割された Java のプログラムであれば、以下のように分割、実行となる。
((( ListNode.java )))
import java.util.* ;
class ListNode {
int data ;
ListNode next ;
ListNode( int d , ListNode n ) {
this.data = d ;
this.next = n ;
}
static void print( ListNode p ) {
for( ; p != null ; p = p.next )
System.out.print( p.data + " " ) ;
System.out.println() ;
}
} ;
((( Main.java )))
import java.util.* ;
public class Main {
public static void main(String[] args) throws Exception {
ListNode a = new ListNode( 11 , new ListNode( 22 , new ListNode( 33 , null ) ) ) ;
ListNode.print( a ) ;
}
}
((( コンパイルと実行 )))
$ javac ListNode.java
$ javac Main.java
$ java Main
この時、ListNode.java , ListNode.class を別フォルダ(例えば module/ListNode.java に保存する場合、java Main にてプログラムを実行する際に、ListNode.class が見つからないといったエラーが出てくる。こういった場合には、javac –classpath module Main.java とか、java –classpath module Main といったように実行するか、環境変数 CLASSPATH に、export CLASSPATH=module:その他… といったように実行に必要な class ファイルが保存されている場所を登録しておく必要がある。
分割コンパイル
複数人でプログラムを開発する場合、1つのファイルを全員で編集するのは混乱してしまう。例えば、ちょうど情報構造論で説明している、リスト処理のようなプログラムであれば、List 構造の構造体、cons(),print() といったList 構造を操作する関数を作る人と、そのそれらの関数を利用するプログラムを書く人に分かれてプログラム開発をすれば混乱も減らせる。そして、それぞれ別のファイルになっている方が開発しやすい。
- list.h : ヘッダファイル – 構造体の宣言や関数のプロトタイプ宣言や変数のextern宣言などを記載
- list.c : リスト処理の cons,print などの処理内容を記載
- main.c : cons,print を使った処理を記載
#include “ヘッダファイル”
自作のヘッダファイルを読み込む場合は、#include “list.h“ のように記載する。
#include で、ヘッダファイルを < > で囲むと、/usr/include フォルダから探してくれる。” “ で囲むと、ソースプログラムと同じフォルダの中からヘッダファイルを探す。
プロトタイプ宣言と extern 宣言
ヘッダファイルには、list.c と main.c の両方で使われるデータ構造、関数、変数の宣言を記載する。関数は、引数の型や返り値の型を記載した struct List* cons( int , struct List*) ; といったプロトタイプ宣言を記載する。変数については、変数の型だけを宣言する extern struct List* stack ; といった extern 宣言を記載する。
// list.h -----------------------------
// リスト構造の宣言
struct List {
int data ;
struct List* next ;
} ;
// リスト操作の関数のプロトタイプ宣言
extern struct List* cons( int , struct List* ) ;
extern void print( struct List* ) ;
// stack の extern 宣言
extern struct List* stack ;
// スタック操作関数のプロトタイプ宣言
extern void push( int ) ;
extern int pop()
// list.c -----------------------------
#include <stdio.h>
#include <stdlib.h>
#include "list.hxx"
// リストの要素を作る
struct List* cons( int x , struct List* n ) {
struct List* ans = (struct List*)malloc( sizeof( struct List ) ) ;
if ( ans != NULL ) {
ans->data = x ;
ans->next = n ;
}
return ans ;
}
// 全要素の出力
void print( struct List* p ) {
for( ; p != NULL ; p = p->next )
printf( "%d " , p->data ) ;
printf( "\n" ) ;
}
// stack の実体
struct List* stack = NULL ;
// スタックに x を保存
void push( int x ) {
stack = cons( x , stack ) ;
}
// スタックの先頭を取り出す
int pop() {
int ans = stack->data ;
struct List* d = stack ;
stack = stack->next ;
free( d ) ;
return ans ;
}
// main.c -----------------------------
#include <stdio.h>
#include "list.hxx"
int main() {
struct List* top = cons( 1 , cons( 2 , cons( 3 , NULL ) ) ) ;
print( top ) ;
push( 11 ) ; push( 22 ) ; push( 33 ) ;
printf( "%d\n" , pop() ) ;
printf( "%d\n" , pop() ) ;
printf( "%d\n" , pop() ) ;
return 0 ;
}
分割コンパイルの作業を確認するために、以下のコマンドを実行してみよう。
((( 一度にコンパイルする方法 ))) guest00@nitfcei:~$ cp /home0/Challenge/seg-compile/* . guest00@nitfcei:~$ gcc list.c main.c guest00@nitfcei:~$ ./a.out # 正しく実行できる。 ((( 失敗するコンパイル ))) guest00@nitfcei:~$ gcc list.c /usr/bin/ld: /usr/lib/gcc/x86_64-linux-gnu/9/../../../x86_64-linux-gnu/Scrt1.o: in function `_start': (.text+0x24): undefined reference to `main' collect2: error: ld returned 1 exit status # list.c の中に main() が無いからエラー guest00@nitfcei:~$ gcc main.c /usr/bin/ld: /tmp/ccxr4Fif.o: in function `main': main.c:(.text+0x17): undefined reference to `cons' /usr/bin/ld: main.c:(.text+0x24): undefined reference to `cons' /usr/bin/ld: main.c:(.text+0x41): undefined reference to `print' : collect2: error: ld returned 1 exit status # main.c の中に、cons(),print(),push(),pop() が無いからエラー ((( プログラムをひとつづつコンパイル ))) guest00@nitfcei:~$ gcc -c list.c # list.o を作る guest00@nitfcei:~$ gcc -c main.c # main.o を作る guest00@nitfcei:~$ gcc list.o main.o # list.o と main.o から a.out を作る guest00@nitfcei:~$ ./a.out # 正しく実行できる。
make と Makefile
上記のように分割コンパイルのためにファイルを分割すると、実行プログラムを生成するには以下のコマンドを実行する必要がある。
- gcc -c list.c (list.o を作る)
- gcc -c main.c (main.o を作る)
- gcc list.o main.o (list.oとmain.oを使って a.out を作る)
また、プログラムのデバッグ作業中ですでに list.o , main.o , a.out が生成されている状態で、main.c の中に間違いを見つけて修正した場合、list.o を作るための 手順1 は不要となる。例えば list.c が巨大なプログラムであれば、手順1を省略できれば、コンパイル時間も短くできる。一方で、どのファイルを編集したから、どの手順は不要…といった判断をプログラマーが考えるのは面倒だったりする。
こういった一部の修正の場合に、必要最小限の手順で目的の実行プログラムを生成するためのツールが make であり、どのファイルを利用してどのファイルが作られるのかといった依存関係と、どういった手順を実行するのかといったことを記述するファイルが Makefile である。
### Makefile ###
# a.out を作るには list.o , main.o が必要
a.out: list.o main.o # 最終的に生成する a.out の依存関係を最初に書く
gcc list.o main.o
# list.o は list.c , list.h に依存
list.o: list.c list.h
gcc -c list.c
# main.o は main.c , list.h に依存
main.o: main.c list.h
gcc -c main.c
clean:; rm *.o a.out # 仮想ターゲット: make clean と打つと、rm *.o a.out を実行してくれる。
Makefile では、依存関係と処理を以下の様に記載する。make コマンドは、ディレクトリ内の Makefile を読み込み、ターゲットファイルのタイムスタンプと依存ファイルのタイムスタンプを比較し、依存ファイルの方が新しい場合(もしくはターゲットファイルが無い場合)、ターゲットを生成するための処理が行われる。
ターゲットファイル: 依存ファイル ...
ターゲットファイルを生成する処理 # 行の先頭の空白は"タブ"を使うこと
理解確認
集合とリスト処理
リスト構造は、必要に応じてメモリを確保するデータ構造であり、データ件数に依存しないプログラム が記述できる。その応用として、集合処理を考えてみる。集合処理の記述には、2進数を使った方式やリストを用いた方法が一般的である。以下にその処理について示す。
bit演算子
2進数を用いた集合処理を説明する前に、2進数を使った計算に必要なbit演算子について復習してみる。
bit演算子は、その数値を2進数表記とした時の各ビットをそれぞれAND,OR,EXOR,NOTなどの計算を行う。
| bit演算子 | 計算の意味 | 関連知識 |
|---|---|---|
| & bit AND | 3 & 5 0011)2 & 0101)2= 0001)2 |
論理積演算子 if ( a == 1 && b == 2 ) … |
| | bit OR | 3 | 5 0011)2 | 0101)2= 0111)2 |
論理和演算子 if ( a == 1 || b == 2 ) … |
| ~ bit NOT | ~5 ~ 00..00,0101)2= 11..11,1010)2 |
論理否定演算子 if ( !a == 1 ) … |
| ^ bit EXOR | 3 ^ 5 0011)2 ^ 0101)2= 0110)2 |
|
| << bit 左シフト | 3 << 2 0011)2 << 2 = 001100)2 |
x << y は |
| >> bit 右シフト | 12 >> 2 1100)2 >> 2 = 11)2 |
x >> y は |
import java.util.*;
public class Main {
public static void main(String[] args) throws Exception {
System.out.println( 12 & 5 ) ; // 1100 & 0101 = 0100 = 4
System.out.println( 12 | 5 ) ; // 1100 | 0101 = 1101 = 13
System.out.println( ~12 & 0xF ) ; // ~1100 & 1111 = 0011 = 3
System.out.println( 3 << 2 ) ; // 0011 << 2 = 1100
System.out.println( 12 >> 2 ) ; // 1100 >> 2 = 0011
System.out.println( ~12 + 1 ) ; // ~0..00001100 + 1 = 1..11110011 + 1 = 1..11110100 = -12
}
}
論理演算子とbit演算子の違い
論理積,論理和という点では、論理演算子&&,|| と bit演算子&,| は複数桁の2進数で計算する違いと思うかもしれないが、論理演算子&&,|| は若干挙動が違う。論理積&&演算子は、左辺の結果が false だと(結果がfalse確定なので) 右辺の計算式や呼び出されない。同じように論理和||演算子は、左辺の結果が true だと(結果がtrue確定なので) 右辺の計算式は呼び出されない。
import java.util.*; public class Main { static boolean boolean_print( boolean yn ) { System.out.print( yn + " " ) ; return yn ; } static int int_print( int yn ) { System.out.print( yn + " " ) ; return yn ; } public static void main(String[] args) throws Exception { boolean ans ; int x ; ans = boolean_print( true ) && boolean_print( true ) ; System.out.println() ; ans = boolean_print( false ) && boolean_print( true ) ; System.out.println() ; ans = boolean_print( true ) || boolean_print( true ) ; System.out.println() ; ans = boolean_print( false ) || boolean_print( true ) ; System.out.println() ; x = int_print( 0 ) & int_print( 1 ) ; System.out.println() ; x = int_print( 1 ) | int_print( 0 ) ; System.out.println() ; } }
- 論理演算子とbit演算子の違い(Paiza.io)
2進数とビットフィールド
例えば、誕生日の年月日の情報を扱う際、20230726で、2023年7月26日を表現することも多い。
しかしこの方法は、この年月日の情報から年(4桁)、月(2桁)、日(2桁)を取り出す処理では、乗算除算が必要となる。通常のCPUであれば、簡単な乗除算は速度的にも問題はないが、組込み系では処理速度の低下も懸念される。
int ymd = 20230726 ; int y , m , d ; y = ymd / 10000 ; m = ymd / 100 % 100 ; d = ymd % 100 ; y = 1965 ; m = 2 ; d = 7 ; ymd = y * 10000 + m * 100 + d ;
こういった処理を扱う際には、2進数の考え方を使って扱う方法がある。
例えば、年は 0..2047 の範囲と考えれば 11 bit で表現でき、月は1..12の範囲であり 4bit で表現可能であり、日は1..31 で 5bit で表現できる。これを踏まえて、年月日を 11+4+5 = 20bit で表す(YYYY,YYYY,YYYM,MMMD,DDDD)なら、以下のプログラムのように書ける。
int ymd = (2024 << 9) + (7 << 5) + 26 ; // YYYY,YYYY,YYYM,MMMD,DDDD int y , m , d ; // 1111,1101,0000,1111,1010 y = ymd >> 9 ; // YYYYYYYYYYY m = (ymd >> 5) & 0xF ; // YYYYYYYYYYYMMMM & 000000000001111 d = (ymd & 0x1F) ; // YYYYYYYYYYYMMMMDDDDD & 00000000000000011111 y = 1965 ; m = 2 ; d = 7 ; ymd = (y << 9) + (m << 5) + d ;
C言語でのビットフィールド
しかし、上記のプログラムでは、いちいち2進数bit演算をイメージする必要があって、プログラムが分かりづらい。C言語では、こういった際にに使うのが ビットフィールドである。
// C言語の場合 (Javaではビットフィールドの構文がない) struct YMD { unsigned int year : 11 ; // ビットフィールドでは、 unsigned int month : 4 ; // 構造体の要素を何ビットで保存するのか unsigned int day : 5 ; // 指定することができる。 } ; struct YMD ymd = { 2023 , 7 , 26 } ; int y , m , d ; y = ymd.year ; m = ymd.month ; d = ymd.day ; ymd.year = 1965 ; ymd.month = 2 ; ymd.day = 7 ;
2進数を用いた集合計算
リストによる集合の前に、もっと簡単な集合処理を考える。
最も簡単な方法は、要素に含まれる=true か 含まれない=false を boolean型の配列に覚える方法であろう。数字Nが集合に含まれる場合は、配列[N]に true を覚えるものとする。この方法で積集合などを記述した例を以下に示す。
import java.util.*;
public class Main {
public static void boolarray_print( boolean[] a ) {
for( int i = 0 ; i < a.length ; i++ )
System.out.print( a[i] ? "T" : "F" ) ;
System.out.println() ;
}
public static void boolarray_and( boolean[] ans , boolean[] a , boolean[] b ) {
for( int i = 0 ; i < a.length ; i++ )
ans[i] = a[i] && b[i] ;
}
public static void boolarray_or( boolean[] ans , boolean[] a , boolean[] b ) {
for( int i = 0 ; i < a.length ; i++ )
ans[i] = a[i] || b[i] ;
}
public static void main(String[] args) throws Exception {
// 0 1 2 3 4 5 6 7 8 9
boolean[] ba = { false, true, true, true, false, false, false, false, false, false } ; // {1,2,3}
boolean[] bb = { false, false, true, false, true, false, true, false, false, false } ; // {2,4,6}
boolean[] bc = { false, false, false, false, true, false, true, false, false, true } ; // {4,6,9}
boolean[] ans = new boolean[ 10 ] ;
boolarray_print( ba ) ;
boolarray_print( bb ) ;
boolarray_and( ans , ba , bb ) ;
boolarray_print( ans ) ;
boolarray_print( bb ) ;
boolarray_print( bc ) ;
boolarray_or( ans , bb , bc ) ;
boolarray_print( ans ) ;
}
}
FTTTFFFFFF // ba
FFTFTFTFFF // bb
FFTFFFFFFF // ba & bb
FFTFTFTFFF // bb
FFFFTFTFFT // bc
FFTFTFTFFT // bb | bc
しかし、上述のプログラムでは、要素に含まれる/含まれないという1bitの情報をboolean型で保存しているが、実体は整数型で保存しているためメモリの無駄となる。
データ件数の上限が少ない場合には、「2進数の列」の各ビットを集合の各要素に対応づけし、要素の有無を0/1で表現する。この方法を用いるとビット演算命令で 和集合、積集合を計算できるので、処理が極めて簡単になる。
2進数を用いた集合計算
扱うデータ件数が少ない場合には、「2進数の列」の各ビットを集合の各要素に対応づけし、要素の有無を0/1で表現する。この方法を用いるとC言語のビット演算命令で 和集合、積集合を計算できるので、処理が極めて簡単になる。
以下のプログラムは、0〜31の数字を2進数の各ビットに対応付けし、 ba = {1,2,3} , bb = {2,4,6} , bc= {4,6,9} を要素として持つ集合で、ba ∩ bb , bb ∪ bc の計算を行う例である。
import java.util.*;
public class Main {
static void bitfield_print( int x ) {
for( int i = 0 ; i < 10 ; i++ )
System.out.print( ((x & (1 << i)) != 0) ? "T" : "F" ) ;
System.out.println() ;
}
public static void main(String[] args) throws Exception {
int ba = (1 << 1) | (1 << 2) | (1 << 3) ; // {1,2,3}
int bb = (1 << 2) | (1 << 4) | (1 << 6) ; // {2,4,6}
int bc = (1 << 4) | (1 << 6) | (1 << 9) ; // {4,6,9}
bitfield_print( ba ) ;
bitfield_print( bb ) ;
bitfield_print( ba & bb ) ;
bitfield_print( bb ) ;
bitfield_print( bc ) ;
bitfield_print( bb | bc ) ;
}
}
有名なものとして、エラトステネスのふるいによる素数計算を2進数を用いて記述してみる。このアルゴリズムでは、各bitを整数に対応付けし、素数で無いと判断した2進数の各桁に1の目印をつけていく方式である。
import java.util.*;
public class Main {
static final int INT_BITS = 31 ;
static int prime = 0 ;
public static void main(String[] args) throws Exception {
// 倍数に非素数の目印をつける
for( int i = 2 ; i <= INT_BITS ; i++ ) {
if ( (prime & (1 << i)) == 0 ) {
for( int j = 2 * i ; j <= INT_BITS ; j += i )
prime |= (1 << j) ;
}
}
// 非素数の目印の無い値を出力
for( int i = 2 ; i <= INT_BITS ; i++ ) {
// 目印のついていない値は素数
if ( (prime & (1 << i)) == 0 )
System.out.println( i ) ;
}
}
}
リスト処理による積集合
前述の方法は、リストに含まれる/含まれないを、2進数の0/1で表現する方式である。しかし、2進数であれば、int で 31要素、long int で 63 要素が上限となってしまう。
しかし、リスト構造であれば、リストの要素として扱うことで、要素件数は自由に扱える。また、今までの授業で説明してきた cons() などを使って表現すれば、簡単なプログラムでリストの処理が記述できる。
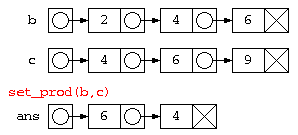
例えば、積集合(a ∩ b)を求めるのであれば、リストa の各要素が、リストb の中に含まれるか find 関数でチェックし、 両方に含まれたものだけを、ans に加えていく…という考えでプログラムを作ると以下のようになる。
import java.util.*;
class ListNode {
int data ;
ListNode next ;
ListNode( int d , ListNode n ) {
this.data = d ;
this.next = n ;
}
static void print( ListNode p ) {
for( ; p != null ; p = p.next )
System.out.print( p.data + " " ) ;
System.out.println() ;
}
static boolean find( ListNode p , int key ) {
for( ; p != null ; p = p.next )
if ( p.data == key )
return true ;
return false ;
}
static ListNode set_prod( ListNode a , ListNode b ) {
ListNode ans = null ;
for( ; a != null ; a = a.next ) {
if ( find( b , a.data ) )
ans = new ListNode( a.data , ans ) ;
}
return ans ;
}
} ;
public class Main {
public static void main(String[] args) throws Exception {
ListNode b = new ListNode( 2 , new ListNode( 4 , new ListNode( 6 , null ) ) ) ;
ListNode c = new ListNode( 4 , new ListNode( 6 , new ListNode( 9 , null ) ) ) ;
ListNode b_and_c = ListNode.set_prod( b , c ) ;
ListNode.print( b_and_c ) ;
}
}
例題として、和集合、差集合などを考えてみよう。
理解確認
- 2進数を用いた集合処理は、どのように行うか?
- リスト構造を用いた集合処理は、どのように行うか?
- 積集合(A ∩ B)、和集合(A ∪ B)、差集合(A – B) の処理を記述せよ。