データ処理において、配列は基本的データ構造だが、動的メモリ確保の説明で述べたように、基本の配列では大きさを変更することができない。これ以外にも、配列は途中にデータを挿入・削除を行う場合、の処理時間を伴う。以下にその問題点を整理し、その解決策であるリスト構造について説明する。
配列の利点と欠点
今までデータの保存には、配列を使ってきたが、配列は添字で場所を指定すれば、その場所のデータを簡単に取り出すことができる。配列には苦手な処理がある。
例えば、配列の中から目的のデータを高速に探す方式として、2分探索法を用いる。処理に要する時間としては となる。
// この関数は見つかったら、見つかった場所、見つからない場合は -1 を返す。
int find( int array[] , int left , int right , int key ) {
// データは left から right-1までに入っているとする。
while( left < right ) {
int mid = (left + right) / 2 ; // 中央の場所
if ( array[ mid ] == key )
return mid ; // 見つかった
else if ( array[ mid ] > key )
right = mid ; // 左半分にある
else
left = mid + 1 ; // 右半分にある
}
return -1 ; // 見つからない
}
int a[] = { 12 , 34 , 41 , 53 , 62 , 79 , 80 } ;
int main() {
int ans = find( a , 0 , 7 , 62 ) ; // 配列 a[] から 62 を探す
printf( "%d¥n" , ans ) ; // 4が表示される
return 0 ;
}
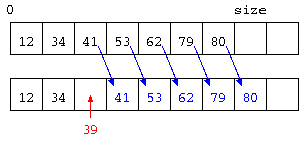
しかし、この配列の中に新たに要素を追加しようとするならば、データは昇順に並んでいる必要があることから、以下のようになるだろう。
void entry( int array[] , int* psize , int key ) {
// データを入れるべき場所を探す処理
for( int i = 0 ; i < *psize ; i++ ) // O(N) の処理だけど、
if ( array[ i ] > key ) // O(log N) でも書けるけど
break ; // 今回は単純に記載する。
if ( i < *psize ) {
// 要素を1つ後ろにずらす処理(A)
for( int j = *psize ; j > i ; j-- ) // O(N)の処理
array[ j ] = array[ j - 1 ] ;
array[ i ] = key ;
} else {
array[ *psize ] = key ;
}
(*psize)++ ;
}
/// よくある間違い ///
/// 上記処理の(A)の部分を以下のように記載した ///
/// 問題点はなにか答えよ ///
// for( int j = i ; j < size ; j++ )
// array[ j + 1 ] = array[ j ] ;
// array[ i ] = key ;
int main() {
int a[ 100 ] ;
int size = 0 ;
int x ;
// 入力された値を登録していく繰り返し処理
while( scanf( "%d" , &x ) == 1 ) {
// x を追加する。
entry( a , &size , x ) ;
}
return 0 ;
}
これで判るように、昇順に並んだ配列にデータを追加する場合、途中にデータを入れる際にデータを後ろにずらす処理が発生する。
この例は、データを追加する場合であったが、不要となったデータを取り除く場合にも、データの場所の移動が必要である。
このことから、昇順に並べられた配列は、データの追加処理の発生頻度が少ない場合は、2分探索法で効率が良いが、データの追加や削除が頻繁に発生する時はあまり効率が良くない。
順序が重要なデータ列で途中へのデータ挿入削除を高速化
例えば、アパート入居者に回覧板を回すことを考える。この中で、入居者が増えたり・減ったりした場合、どうすれば良いか考える。
以下の説明のような方法であれば、自分の所に回覧板が回ってきたら、次の入居者の部屋番号さえわかっていれば、スムーズに回覧板を回すことができる。
101 102 103 104 105 106 アパートの番号 [ 105 | 106 | -1 | 102 | 104 | 103 ] 回覧板を回す次の人の部屋番号 101号室の次は、105号室、 105号室の次は、104号室、 : 106号室の次は、103号室、 103号室の次は、おしまい(-1)
このように「次のデータの場所」という概念を使うと、データの順序を持って扱うことができる。これをプログラムにしてみよう。
struct LIST {
int data ; // 実際のデータ
int next ; // 次のデータの配列の添字
} ;
struct LIST array[] = {
/*0*/ { 11 , 2 } ,
/*1*/ { 67 , 3 } , // 末尾にデータ34を加える
/*2*/ { 23 , 4 } , // { 23 , 5 } ,
/*3*/ { 89 , -1 } , // 末尾データの目印
/*4*/ { 45 , 1 } ,
/*5*/ { 0 , 0 } , // { 34 , 4 } ,
} ;
int main() {
for( int idx = 0 ; idx >= 0 ; idx = array[ idx ].next ) {
printf( "%d¥n" , array[ idx ].data ) ;
}
return 0 ;
}
この方法を取れば、途中にデータ入れたり、抜いたりする場合に、データの移動を伴わない。(O(N)の処理が発生しない)
しかし、配列をベースにしているため、配列の上限サイズを超えて格納することはできない。そこで、必要に応じてメモリを確保するテクニックを導入する。
リスト構造
リスト構造は、データと次のデータへのポインタで構成され、必要に応じてメモリを確保することで、配列を使わない。また、次のデータへのポインタでつなげているため、途中へのデータ挿入が簡単にできるようにする。
struct List {
int data ; // データ
struct List* next ; // 次のデータへのポインタ
} ;
int main() {
struct List* top ; // 配列の先頭のデータ
struct List* p ;
top = (struct List*)malloc( sizeof( struct List ) ) ;
top->data = 111 ;
top->next = (struct List*)malloc( sizeof( struct List ) ) ;
top->next->data = 222 ;
top->next->next = (struct List*)malloc( sizeof( struct List ) ) ;
top->next->next->data = 333 ;
top->next->next->next = NULL ; // 必ず、末尾データの目印をつける!
for( p = top ; p != NULL ; p = p->next ) {
printf( "%d¥n" , p->data ) ;
}
return 0 ;
}
補助関数
上記のプログラムでは、(struct…)malloc(sizeof(…))を何度も記載し、プログラムが分かりにくいので、以下に示す補助関数を使うと、シンプルに記載できる。
struct List* cons( int x , struct List* n ) {
struct List* ans ;
ans = (struct List*)malloc( sizeof( struct List ) ) ;
if ( ans != NULL ) {
ans->data = x ;
ans->next = n ;
}
return ans ;
}
struct List* top ;
top = cons( 111 , cons( 222 , cons( 333 , NULL ) ) ) ;
補助関数の名前の cons は、constructor の略であり、古くから使われている List Processor(LISP) というプログラム言語でのリスト(セル)を生成する関数が cons 。
LISPと関数型プログラミング言語
LISPの歴史は長く、最古のFORTRAN,COBOLに次ぐ3番目ぐらい。最初は、人工知能のプログラム開発のための関数型プログラミング言語として作られた。特徴として、データもプログラムもすべてリスト構造(S式)で表すことができ、プログラムは関数型に基づいて作られる。
関数型プログラミングは、Ruby や Python でも取り入れられている。関数型プログラミングは、処理を関数をベースに記述することで「副作用を最小限にすることができ」、極端な話をすればループも再帰呼出しで書けばいい…。
LISPの処理系は、最近では Scheme などが普通だが、プログラムエディタの Emacs は、内部処理が LISP で記述されている。