再帰呼び出しと再帰方程式
再帰関数と再帰方程式
再帰関数は、自分自身の処理の中に「問題を小さくした」自分自身の呼び出しを含む関数。プログラムには問題が最小となった時の処理があることで、再帰の繰り返しが止まる。
// 階乗 (末尾再帰)
int fact( int x ) {
if ( x <= 1 )
return 1 ;
else
return x * fact( x-1 ) ;
}
// ピラミッド体積 (末尾再帰)
int pyra( int x ) {
if ( x <= 1 )
return 1 ;
else
return x*x + pyra( x-1 ) ;
}
// フィボナッチ数列 (非末尾再帰)
int fib( int x ) {
if ( x <= 2 )
return 1 ;
else
return fib( x-1 ) + fib( x-2 ) ;
}
これらの関数の結果について考えるとともに、この計算の処理時間を説明する。 最初のfact(),pyra()については、 x=1の時は、関数呼び出し,x<=1,return といった一定の処理時間を要し、 で表せる。 x>1の時は、関数呼び出し,x<=1,*,x-1,returnの処理(Tb)に加え、x-1の値で再帰を実行する処理時間T(N-1)がかかる。 このことから、
で表せる。
} 再帰方程式
このような再帰を使って表した式は再帰方程式と呼ばれる。これを代入によって解けば、一般式 が得られる。
T(1)=Ta
T(2)=Tb+T(1)=Tb+Ta
T(3)=Tb+T(2)=2×Tb+Ta
:
T(N)=Tb+T(N-1)=Tb + (N-2)×Tb+Ta
一般的に、再帰呼び出しプログラムは(考え方に慣れれば)分かりやすくプログラムが書けるが、プログラムを実行する時には、局所変数や関数の戻り先を覚える必要があり、深い再帰ではメモリ使用量が多くなる。
ただし、fact() や pyra() のような関数は、プログラムの末端で再帰が行われている。(fib()は、再帰の一方が末尾ではない)
このような再帰は、末尾再帰と呼ばれ、関数呼び出しの return を、再帰処理の先頭への goto 文に書き換えるといった最適化が可能である。言い換えるならば、末尾再帰の処理は繰り返し処理に書き換えが可能である。このため、末尾再帰の処理をループにすれば再帰のメモリ使用量の問題を克服できる。
再帰を含む一般的なプログラム例
ここまでの再帰方程式は、再帰の度にNの値が1減るものばかりであった。もう少し一般的な再帰呼び出しのプログラムを、再帰方程式で処理時間を分析してみよう。
以下のプログラムを実行したらどんな値になるであろうか?それを踏まえ、処理時間はどのように表現できるであろうか?
int array[ 8 ] = {
3 , 6 , 9 , 1 , 8 , 2 , 4 , 5 ,
} ;
int sum( int a[] , int L , int R ) { // 非末尾再帰
if ( R - L == 1 ) {
return a[ L ] ;
} else {
int M = (L + R) / 2 ;
return sum( a , L , M ) + sum( a , M , R ) ;
}
}
int main() {
printf( "%d¥n" , sum( array , 0 , 8 ) ) ;
return 0 ;
}
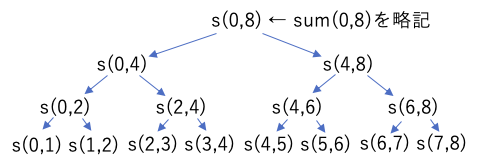
このプログラムでは、配列の合計を計算しているが、引数の L,R は、合計範囲の 左端・右端を表している。そして、再帰のたびに2つに分割して解いている。
このような、処理を分割し、分割したそれぞれを再帰で計算し、その処理結果を組み合わせて最終的な結果を求めるような処理方法を、分割統治法と呼ぶ。
このプログラムでは、対象となるデータ件数(R-L)をNとおいた場合、実行される命令からsum()の処理時間Ts(N)は次の再帰方程式で表せる。
← Tβ + (L〜M)の処理時間 + (M〜R)の処理時間
これを代入の繰り返しで解いていくと、
ということで、このプログラムの処理時間は、 で表せる。
再帰方程式の事例として、ハノイの塔の処理時間について説明し、 数学的帰納法での証明を示す。
ハノイの塔
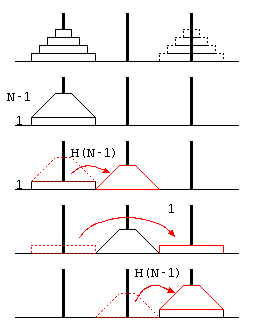
ハノイの塔は、3本の塔にN枚のディスクを積み、(1)1回の移動ではディスクを1枚しか動かせない、(2)ディスクの上により大きいディスクを積まない…という条件で、山積みのディスクを目的の山に移動させるパズル。
一般解の予想
ハノイの塔の移動回数を とした場合、 少ない枚数での回数の考察から、 以下の一般式で表せることが予想できる。
… ①
この予想が常に正しいことを証明するために、ハノイの塔の処理を、 最も下のディスク1枚と、その上の(N-1)枚のディスクに分けて考える。
再帰方程式
上記右の図より、N枚の移動をするためには、上に重なるN-1枚を移動させる必要があるので、
… ②
… ③
ということが言える。(これがハノイの塔の移動回数の再帰方程式)
ディスクが枚の時、予想が正しいのは明らか①,②。
ディスクが 枚で、予想が正しいと仮定すると、
枚では、
… ③より
… ①を代入
となり、 枚でも、予想が正しいことが証明された。 よって数学的帰納法により、1枚以上で予想が常に成り立つことが証明できた。
理解度確認
- 前再帰の「ピラミッドの体積」pyra() を、ループにより計算するプログラムを記述せよ。
- 前講義での2分探索法のプログラムを、再帰によって記述せよ。(以下のプログラムを参考に)。また、このプログラムの処理時間にふさわしい再帰方程式を示せ。
- 再帰のフィボナッチ関数 fib() の処理時間にふさわしい再帰方程式を示せ。
int a[ 10 ] = {
7 , 12 , 22 , 34 , 41 , 56 , 62 , 78 , 81 , 98
} ;
int find( int array[] , int L , int R , int key ) { // 末尾再帰
// 目的のデータが見つかったら 1,見つからなかったら 0 を返す。
if ( __________ ) {
return ____ ; // 見つからなかった
} else {
int M = _________ ;
if ( array[ M ] == key )
return ____ ;
else if ( array[ M ] > key )
return find( array , ___ , ___ , key ) ;
else
return find( _____ , ___ , ___ , ___ ) ;
}
}
int main() {
if ( find( a , 0 , 10 , 56 ) )
printf( "みつけた¥n" ) ;
}
再帰を使ったソートアルゴリズム
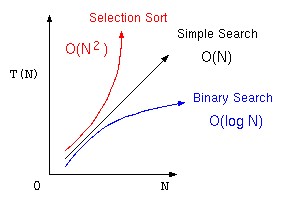
データを並び替える有名なアルゴリズムの処理時間のオーダは、以下の様になる。
この中で、高速なソートアルゴリズムは、クイックソート(最速のアルゴリズム)とマージソート(オーダでは同程度だが若干効率が悪い)であるが、ここでは、再帰方程式で処理時間をイメージしやすい、マージソートにて説明を行う。
マージソートの分析
マージソートは、与えられたデータを2分割し、 その2つの山をそれぞれマージソートを行う。 この結果の2つの山の頂上から、大きい方を取り出す…という処理を繰り返すことで、 ソートを行う。
このことから、再帰方程式は、以下のようになる。
この再帰方程式を、N=1,2,4,8…と代入を繰り返していくと、 最終的に処理時間のオーダが となる。
:
よって、
選択法とクイックソートの処理時間の比較
データ数 N = 20 件でソート処理の時間を計測したら、選択法で 10msec 、クイックソートで 20msec であった。
- データ件数 N = 100 件では、選択法,クイックソートは、それぞれどの程度の時間がかかるか答えよ。
- データ件数何件以上なら、クイックソートの方が高速になるか答えよ。
設問2 は、通常の関数電卓では求まらないので、数値的に方程式を解く機能を持った電卓が必要。
構造体からオブジェクト指向プログラミング
構造体でオブジェクト指向もどき
前回の講義では、構造体渡しを使ったプログラミングをすることで、データ(オブジェクト)に対して命令をするプログラミングスタイルについて説明をした。これによりデータ隠蔽化・手続き隠蔽化を行うことができる。これらをまとめて隠蔽化とかブラックボックス化という。
例えば、名前と年齢の構造体で処理を記述する場合、 以下の様な記載を行うことで、データ設計者とデータ利用者で分けて 仕事ができる。
// この部分はデータ構造の設計者が書く
// データ構造を記述
struct Person {
char name[10] ;
int age ;
} ;
// データに対する処理を記述
void set_Person( struct Person* p , char s[] , int a ) {
// ポインタの参照で表記
strcpy( (*p).name , s ) ;
(*p).age = a ;
}
void print_Person( struct Person* p ) {
// アロー演算子で表記 "(*p).name" は "p->name" で書ける
printf( "%s %d¥n" ,
p->name , p->age ) ;
}
// この部分は、データ利用者が書く
int main() {
// Personの中身を知らなくてもいいから配列を定義(データ隠蔽)
struct Person saitoh ;
set_Person( &saitoh , "saitoh" , 55 ) ;
struct Person table[ 10 ] ; // 初期化は記述を省略
for( int i = 0 ; i < 10 ; i++ ) {
// 出力する...という雰囲気で書ける(手続き隠蔽)
print_Person( &table[i] ) ;
}
return 0 ;
}
こういった隠蔽化をすることにより、データ構造の中身やその手続きの内部を記述するプログラマーと、そのデータや手続きを使うプログラマーに分かれて仕事をすることができるようになる。たとえ1人であったとしても、原因を究明する時に中身の問題か使う側の問題かを切り分けることが容易となり、プログラム作成の効率が良くなる。
C++のクラスで表現
上記のプログラムをそのままC++に書き直すと以下のようになる。
#include <stdio.h>
#include <string.h>
// この部分はクラス設計者が書く
class Person {
private: // クラス外からアクセスできない部分
// データ構造を記述
char name[10] ; // メンバーの宣言
int age ;
public: // クラス外から使える部分
// データに対する処理を記述
void set( char s[] , int a ) { // メソッドの宣言
// pのように対象のオブジェクトを明記する必要はない。
strcpy( name , s ) ;
age = a ;
}
void print() {
printf( "%s %d¥n" , name , age ) ;
}
} ; // ← 注意ここのセミコロンを書き忘れないこと。
// この部分はクラス利用者が書く
int main() {
Person saitoh ;
saitoh.set( "saitoh" , 55 ) ;
saitoh.print() ;
// 文法エラーの例
printf( "%d¥n" , saitoh.age ) ; // phoneはprivateなので参照できない。
return 0 ;
}
この様にC++のプログラムに書き換えたが、内部の処理は元のC言語と同じであり、オブジェクトへの関数呼び出し saitoh.set(…) などが呼び出されても、set() は、オブジェクトのポインタを引数して持つ関数として、機械語が生成されるだけである。
用語の解説:C++のプログラムでは、データ構造とデータの処理を、並行しながら記述する。 データ構造に対する処理は、メソッド(method)と呼ばれる。 データ構造とメソッドを同時に記載したものは、クラス(class)と呼ぶ。 そのデータに対し具体的な値や記憶域が割り当てられたものをオブジェクト(object)と呼ぶ。
C++では隠蔽化をさらに明確にするために、private: や public: を指定できる。private: は、そのメソッドの中でしか使うことができない要素や関数であり、public: は、メソッド以外からでも参照したり呼出したりできる。オブジェクト指向でプログラムを書くとき、データ構造や関数の処理方法は、クラス内部の設計者しか触れないようにしておけば、その内部を改良することができる。しかし、クラスの利用者が勝手に内部データを触っていると、内部設計者が改良するとそのプログラムは動かないものになってしまう。
隠蔽化を的確に行うことで、クラス内部を常に改良できるがこれをリファクタリングと呼ぶ。
クラス限定子
前述のプログラムでは、class 宣言の中に関数内部の処理を記述していた。しかし関数の記述が長い場合は、書ききれないこういう場合はクラス限定子を使って記述する。
class Person {
private:
char name[10] ;
int age ;
public:
// メソッドのプロトタイプ宣言
void set( char s[] , int a) ;
void print() ;
} ;
void Person::set( char s[] , int a ) {
strcpy( name , s ) ;
age = a ;
}
void Person::print() {
printf( "%s %d¥n" , name , age ) ;
}
inline 関数と開いたサブルーチン
オブジェクト指向では、きわめて簡単な処理な関数を使うことも多い。
例えば、上記のプログラム例で、クラス利用者に年齢を読み出すことは許しても書き込みをさせたくない場合、以下のような、関数を定義する。(getterメソッド)逆に、値の代入専用のメソッドは、setterメソッドと呼ぶ
class Person { private: char name[10] ; int age ; public: // メソッドのプロトタイプ宣言 inline int get_age() { return age ; } // getter inline void set_age( int a ) { age = a ; } // setter } ;ここで inline とは、開いた関数(開いたサブルーチン)を作る指定子である。通常、機械語を生成するとき中身を参照するだけの機械語と、get_age() を呼出したときに関数呼び出しを行う機械語が作られる(閉じたサブルーチン)が、age を参照するだけのために関数呼び出しの機械語はムダが多い。inline を指定すると、入り口出口のある関数は生成されず、get_age() の処理にふさわしい age を参照するだけの機械語が生成される。
# 質問:C言語で開いたサブルーチンを使うためにはどういった機能があるか?
コンストラクタとデストラクタ
プログラムを記述する際、よくある間違いでは、初期化忘れや終了処理忘れがある。
このための機能がコンストラクタ(構築子)とデストラクタ(破壊子)という。
コンストラクタは、返り値を記載しない関数でクラス名(仮引数…)の形式で宣言し、オブジェクトの宣言時に初期化を行う処理として呼び出される。デストラクタは、~クラス名() の形式で宣言し、オブジェクトが不要となる際に、自動的に呼び出し処理が埋め込まれる。
class Person {
private:
// データ構造を記述
char name[10] ;
int age ;
public:
Person( char s[] , int a ) { // コンストラクタ
strcpy( name , s ) ;
age = a ;
}
~Person() { // デストラクタ
print() ;
}
void print() {
printf( "%s %d¥n" , name , age ) ;
}
} ;
int main() {
Person saitoh( "saitoh" , 55 ) ; // オブジェクトsaitohを"saitoh"と55で初期化
return 0 ;
// main を抜ける時にオブジェクトsaitohは不要になるので、
// デストラクタが自動的に呼び出され、"saitoh 55" が表示。
}
オーダー記法と再帰処理の導入
先週に、2重の繰り返し処理の時間分析をやったので、次のステップに。
2分探索法の処理時間
データを探す処理において、単純検索より速い方法ということで、2分探索法の処理速度見積もりを行う。
// 2分探索法 O(log N)
int a[ 1000 ] = { 対象となるデータ } ;
int size = N ; // データ数 N
int L = 0 ; // L=下限のデータの場所
int R = size ; // R=上限のデータ+1の場所
while( L != R ) {
int M = (L + R) / 2 ; // 計算は整数型で行われることに注意
if ( a[M] == key ) // 見つかった
break ;
else if ( a[M] < key ) // |L |M. |R
L = M + 1 ; // |----------|-+---------|
else // |L---------|M|
R = M ; // |M+1------|R
}
上記のようなプログラムの場合、処理に要する時T(N)は、
処理は、対象となるデータ件数が繰り返し毎に半分(正確には(N-1)/2だけどここでは厳密な分析はしない)となり、対象データ件数が1件になれば処理が終わる。このことから、データ件数Nとループ回数Mの間には以下の関係が成り立つ。
よって の関係が成り立つ。よって、
は、以下のように表せる。
# T(N)の式の中では、logの底については書かないことが一般的。(後の練習問題を参照)
単純なソート(最大選択法)の処理時間
次に、並べ替え処理の処理時間について考える。
int a[ 1000 ] = { 対象となるデータ } ;
int size = N ;
for( int i = 0 ; i < size - 1 ; i++ ) {
int tmp ;
// i..size-1 の範囲で一番大きいデータの場所を探す
int m = i ;
for( int j = i + 1 ; j < size ; j++ ) {
if ( a[j] > a[m] )
m = j ;
}
// 一番大きいデータを先頭に移動
tmp = a[i] ;
a[i] = a[m] ;
a[m] = tmp ;
}
このプログラムの処理時間T(N)は… (参考 数列の和の公式)
となる。
オーダー記法
ここまでのアルゴリズムをまとめると以下の表のようになる。ここで処理時間に大きく影響する部分は、最後の項の部分であり、特にその項の係数は、コンピュータの処理性能に影響を受けるが、アルゴリズムの優劣を考える場合は、それぞれ、
の部分の方が重要である。
| 単純サーチ | |
| 2分探索法 | |
| 最大選択法 |
そこで、アルゴリズムの優劣を議論する場合は、この処理時間の見積もりに最も影響する項で、コンピュータの性能によって決まる係数を除いた部分を抽出した式で表現する。これをオーダー記法と言う。
| 単純サーチ | オーダーNのアルゴリズム | |
| 2分探索法 | オーダー log N のアルゴリズム | |
| 最大選択法 | オーダー N2 のアルゴリズム |
練習問題
- ある処理のデータ数Nに対する処理時間が、
であった場合、オーダー記法で書くとどうなるか?
- コンピュータで2分探索法で、データ100件で10[μsec]かかったとする。
データ10000件なら何[sec]かかるか?
(ヒント: 底変換の公式) の処理時間を要するアルゴリズムを、オーダー記法で書くとどうなるか?また、このようなアルゴリズムの例を答えよ。
の処理時間を要するアルゴリズムを、オーダー記法で書くとどうなるか?
(ヒント: ロピタルの定理)
- 2と4の解説
- 1は、N→∞において、N2<<2Nなので、O(2N) 。厳密に回答するなら、練習問題4と同様の説明を行う。
- 3は、O(1)。誤答の例:O(0)と書いちゃうと、T(N)=Tα×0=0になってしまう。事例は、電話番号を、巨大配列の”電話番号”番目の場所に記憶するといった方法。(これはハッシュ法で改めて講義予定)
再帰呼び出しの予習
次の講義の基礎を確認という意味で、再帰呼出しと簡単な処理の例を説明する。
最初に定番の階乗(fact)

次に、フィボナッチ数列の場合

次の講義への導入問題
ここで示す導入問題をすべて答えるには、若干の予習が必要です。まずはどういう考え方をすれば解けるかな…を考えてみてください。
- fact(N)の処理時間を、
のような式で表現し、処理時間をオーダ記法で答えよ。
- 以下のプログラムの実行結果を答えよ。また、関数sum()の処理時間を対象となるデータ件数N=R-Lを用いて
のような式で表現せよ。
int a[] = { 1 , 5 , 8 , 9 , 2 , 3 , 4 , 7 } ;
int sum( int a[] , int L , int R ) {
if ( R-L == 1 ) {
return a[L] ;
} else {
int M = (L + R) / 2 ;
return sum( a , L , M ) + sum( a , M , R ) ;
}
}
int main() {
printf( "%d¥n" , sum( a , 0 , 8 ) ) ;
return 0 ;
}
創造工学演習・予備実験・パズル問題
プログラミングコンテストの競技部門では、パズルのような組み合わせ問題が 出題されることが多い。また、課題部門や自由部門であっても、複数の条件の組み合わせの中から最良のものを選ぶといった処理も求められる。そこで、この予備実験では、きわめて単純なパズル問題(組み合わせ問題) のプログラムについて扱う。
組み合わせ問題の基礎
簡単な問題として「100未満の整数の値を3つ選び、その値を辺の長さとした場合、 直角三角形となるものをすべて表示する。」について考える。
一番簡単な方法は、以下となるであろう。
#include <stdio.h>
#include <math.h>
#include <time.h>
// 整数比の直角三角形の一覧を求める。
void integer_triangle( int n ) {
for( int a = 1 ; a < n ; a++ ) {
for( int b = 1 ; b < n ; b++ ) {
// 一番ダサい方法
for( int c = 1 ; c < n ; c++ ) {
if ( a*a + b*b == c*c ) {
printf( "%d %d %d\n" , a , b , c ) ;
}
}
}
}
}
int main() {
integer_triangle( 100 ) ;
return 0 ;
}
しかしこのプログラムの欠点としては、100×100×100回のループで無駄な処理が多い。
ループ回数を減らすだけなら、最も内側の処理を、計算で整数値か確認すればいい。
void integer_triangle( int n ) {
for( int a = 1 ; a < n ; a++ ) {
for( int b = 1 ; b < n ; b++ ) {
// ココも改良できるよね?
int d = a*a + b*b ;
int c = (int)sqrt( d ) ;
// 斜辺Cの整数値を求め、改めて確認する。
if ( c*c == d ) {
printf( "%d %d %d\n" , a , b , c ) ;
}
}
}
}
(1) 計算誤差の問題を考えてみよう。
たとえば、3:4:5の直角三角形で、3*3+4*4 = 25 だが、sqrt(25)は実数で計算するから、 計算誤差で4.99999で求まったらどうなるだろうか?
1~100までの数値で、”int c = sqrt( (double)(i*i) ) ;” を計算してみて、 異なる値が求まることはあるか? 多少の計算誤差があっても正しく処理が行われるにはどうすればいいか、考えてみよう。
(2) 無駄な答えについて考えてみよう。
このプログラムの答えでは、簡単な整数比の答えの「整数倍の答え」も表示されてしまう。 たとえば、(3:4:5)の答えのほかに、(6:8:10)も表示される。 こういった答えを表示しないようにするにはどうすればよいか?
また、この2つのプログラムの処理時間を実際に比べてみる。
#include <stdio.h>
#include <time.h>
int main() {
time_t start , end ;
// time() 関数は、秒数しか求まらないので、
// あえて処理を1000回繰り返し、数秒かかる処理にする。
start = time( NULL ) ;
for( int i = 0 ; i < 1000 ; i++ ) {
// ただし、関数内のprintfをコメントアウトしておくこと
integer_triangle( 100 ) ;
}
end = time( NULL ) ;
printf( "%lf\n" , difftime( end , start ) ) ;
return 0 ;
}
再帰プログラミング
組み合わせ問題では、forループの多重の入れ子で問題を解けない場合が多い。 (書けないことはないけど無駄なループで処理が遅くなるか、入れ子段数が可変にできない。)
こういった場合には、再帰プログラミングがよく利用される。 もっとも簡単な再帰の例として、階乗のプログラムを考える。 通常であれば、以下のような for ループで記述することになるだろう。
// 階乗の計算
int fact( int x )
{ // ループ
int f = 1 ;
for( int i = 2 ; i <= x ; i++ )
f = f * i ;
return f ;
}
再帰呼び出しでは、関数の処理の中に、自分自身の関数呼び出しが含まれる。 また、無限に自分自身を呼び出したら処理が止まらないので、 問題を一つ小さくして、これ以上小さくできないときは処理を止めるように記述する。
int fact( int x )
{ // 再帰呼び出し
if ( x <= 1 )
return 1 ;
else
return x * fact( x - 1 ) ;
}
ここ以降は、指定長さを指定辺の組み合わせで作る課題と、後に述べるFlood-fill 課題の選択とする。
指定長を指定辺の組み合わせで作る(テーマ1)
再帰を使った簡単なパズル問題として、以下のプログラムを作成したい。
配列の中に、複数の辺の長さが入っている。これを組み合わせて指定した長さを作れ。 使用する辺はできるだけ少ない方がよい。
int a[] = { 4 , 5 , 2 , 1 , 3 , 7 } ;
(例) 辺の長さ10を作るには、(5,4,1)とか(7,3)などが考えられる。
これは、ナップサック問題の基本問題で、容量の決まったナップサックに最大量入れる組合せを求めるのと同じである。
このプログラムを解くには…
10 を [4,5,2,1,3,7] で作るには... (0) 6=10-4 を [4|5,2,1,3,7]で作る。 (1) 5=10-5 を [5|4,2,1,3,7]で作る。 (2) 8=10-2 を [2|5,4,1,3,7]で作る。 (3) 9=10-1 を [1|5,2,4,3,7]で作る。 (4) 7=10-3 を [3|5,2,1,4,7]で作る。 (5) 3=10-7 を [7|5,2,1,3,4]で作る。
そこで、ここまでの考えを、以下のようなプログラムで記述してみる。
# まだ再起呼び出しにはしていない。
// 指定されたデータを入れ替える。
void swap( int*a , int*b )
{ int x = *a ;
*a = *b ;
*b = x ;
}
void check( int array[] , int size , int len , int n )
{
// array[] 配列
// size 配列サイズ
// len 作りたい長さ
// n 使った個数
for( int i = n ; i < size ; i++ ) {
// i番目を先頭に...
swap( &array[ n ] , &array[ i ] ) ;
printf( "check( array , %d , %d , %d )\n" ,
size , len - array[ n ] , n+1 ) ;
// 最初のswapでの変更を元に戻す。
swap( &array[ i ] , &array[ n ] ) ;
}
}
int main() {
int a[] = { 4 , 5 , 2 , 1 , 3 , 7 } ;
check( a , 6 , 10 , 0 ) ;
}
(1) これを再帰呼び出しにしてみよう。どう書けばいい?
void check( int array[] , int size , int len , int n )
{
// array[] 配列
// size 配列サイズ
// len 作りたい長さ
// n 使った個数
if ( len < 0 ) {
// 指定した丁度の長さを作れなかった。
;
} else if ( len == 0 ) {
// 指定した長さを作れたので答えを表示。
for( int i = 0 ; i < n ; i++ ) {
printf( "%d " , array[ i ] ) ;
}
printf( "\n" ) ;
} else {
// 問題を一つ小さくして再帰。
for( int i = n ; i < size ; i++ ) {
swap( &array[ n ] , &array[ i ] ) ;
printf( "check( array , %d , %d , %d )\n" ,
size , len - array[ n ] , n+1 ) ;
check( array , size , len - array[ n ] , n + 1 ) ;
swap( &array[ i ] , &array[ n ] ) ;
}
}
}
(2) 少ない組み合わせの方がポイントが高い場合には、プログラムをどう変更する?
(3) 答えが1つだけで良い場合は、プログラムをどう変更する?
(4) このプログラムでは、冗長な答えがあるか?ないか?検討せよ。
(5) 前設問の整数比直角三角形のプログラムで、冗長な答えを削除するプログラムを作成せよ。
# レポートでは、(2),(3),(4)を検討した結果を実験すること。(5)までチャレンジした人は(2),(3),(4)の説明は簡単に記載するだけで良い。
Flood fill アルゴリズム
前の問題は、今年度のプログラミングコンテストの課題のパズルとは、方向性が違うので、今年度のプロコンの競技部門に近いパズルネタで演習。(Wikipedia Flood-fill参照)
以下の image のような2次元配列が与えられたら、指定座標(x,y)を中心に周囲を塗りつぶす処理を作成せよ。
include <stdio.h>
// *は壁 SPCは白 この領域の指定位置を#で塗りつぶす。
char image1[10][10] = { // (4,4)始点で塗りつぶし後
"*********" , // *********
"* * *" , // * *###*
"* * *" , // * *###*
"* * *" , // * *####*
"*** ***" , // ***###***
"* * *" , // *####* *
"* * *" , // *###* *
"* * *" , // *###* *
"*********" , // *********
} ;
char image2[10][10] = { // 応用問題用の画像例
"*********" , // * のような隙間は通り抜けられる
"* * *" , // * ようにするにはどうすればいい?
"* ** *" , // **
"* ** *" , // ** これは通り抜けられない
"*** ***" , // **
"* * *" ,
"* * *" ,
"* * *" ,
"*********" ,
} ;
// 盤面を表示
void print_image( char image[10][10] ) {
for( int y = 0 ; y < 9 ; y++ ) {
for( int x = 0 ; x < 9 ; x++ ) {
printf( "%c" , image[y][x] ) ;
}
printf( "\n" ) ;
}
}
// 再帰呼び出しを使った flud_fill アルゴリズム
void flood_fill( char image[10][10] , int x , int y , char fill ) {
// image: 塗りつぶす画像
// x,y: 塗りつぶす場所
// fill: 書き込む文字
// 指定座標が空白なら
if ( image[y][x] == ' ' ) {
// その座標を埋める
image[y][x] = fill ;
//////////////////////////////////////
// ここに周囲をflud_fillする処理を書く //
//////////////////////////////////////
}
}
int main() {
print_image( image1 ) ;
flood_fill( image1 , 4 , 4 , '#' ) ;
print_image( image1 ) ;
return 0 ;
}
応用問題
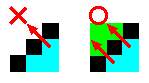
Wikipediaのflood-fill のプログラムの説明のアルゴリズムでは、左図黒のような斜めに並んだブロックは、境界として通り抜けられないようにつくられている。
そこで、斜めに並んだブロックは通り抜けられるルールとした場合のプログラムを記述せよ。
レポート提出
レポートでは、指定長を辺の組み合わせで作るテーマか、Flood-fill のテーマのいずれかにて、以下の内容をまとめてレポートとして提出すること。
-
- レポートの説明(自分の選んだテーマと自分なりの説明)
- プログラムリスト
- 動作確認の結果
緊急連絡システムのicloud問題解決
緊急連絡システムを運営しているけど、最近 icloud.com 宛のメールが届かないといった問題が発生していた。
いくつかのサイトでは、MXレコードを引く際の DNS の情報が大きい場合、qmail が失敗するなどの情報から、対処などを施していたが、icloud の配信でこういった症状が出ていた。
色々と調べてみたが、icloud.com は、メールの X-Header が含まれると、受信を拒否するのが原因ということが見えてきた。
緊急連絡システムでは、トラブルが発生した際の履歴を追えるように、X-EMC-…. という拡張ヘッダを埋め込んでいた。
今回、icloud.com, mac.com, me.com のメールアドレスの場合は、X-EMC- を付けないように処理を加えたところ、無事にメールが送信できることが確認できた。
しかし、こういうキャリア毎の事情は、わからないわ…(x_x;;