ソートアルゴリズムの処理時間で、選択法よりクイックソートが有利になる分岐点を求める問題で、

の結果が、N=53.1 になる…との説明が判らないとの質問。# 53.017 が正しいとの結果だったが。

あてずっぽうな計算方法

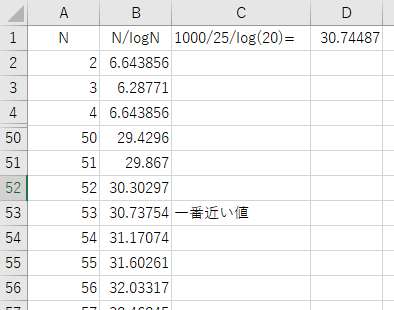
Excelで実際に計算すればいい。B列2行目に =A2/LOG(A2) を入れて、A列に2,3,…. と数字を入れて変化させて、30.74 に近い場所を探すと53となった。# 手抜きだな!

ニュートン法で解く

方程式で解けない場合は、ニュートン法 f(x)=0 の式でxの値を求める…のが定番の方法。

この場合は f(x) = x/log(x) – 1000/25/log(20) として、ニュートン法の漸化式を解けばいい。
ちょいとプログラムを書いてみた。

((( nlogn.cxx )))
#include <stdio.h>
#include <math.h>

// N/logN = 1000/25/log20 をニュートン法で解く                                                                          
//                                                                                                                      
//      f(x) = x/log(x) - 1000/25/log20                                                                                 
//      f'(x) = log(10) (log(x) - 1) / log(x)^2                                                                         
//                                                                                                                      
//      x <= x + f(x) / f'(x)                                                                                           

//      要注意 C言語のlog関数                                                                                           
//              log(x) = 自然対数を底とするlog                                                                          
//              log10(x) = 10を底とするlog                                                                              

double f( double x ) {
  return x / log10(x) - 1000.0/25.0/log10(20.0) ;
}

double df( double x ) {
  return log(10.0) * ( log(x) - 1.0 ) / pow( log(x) , 2.0 ) ;
}

int main() {
  double x = 5.0 ;

  for( int i = 0 ; i < 5 ; i++ ) {
    double f1 = f(x) ;
    double f2 = df(x) ;
    x = x - f1 / f2 ;
    printf( "%d %lf\n" , i , x ) ;
  }
  return 0 ;
}

((( 実行結果 )))
$ g++ nlogn.cxx
$ ./a.out
0 48.547041
1 52.983539
2 53.016894
3 53.016896
4 53.016896

• n/log(n)の微分の計算が面倒だったので、Wolfram Alpha を使ったのは内緒だ! 学生さんは、こーゆー手抜きをしないこと。
• log(x)の計算で、log_e(x) と log₁₀(x) を使い分けるのがキーポイント。
  • Excel では、log_e(x) は、LN(x) 、log₁₀(x) は、LOG10(x)
  • C言語では、log_e(x) は、log(x) 、log₁₀(x) は、log10(x)

うーむ、Webの資料では、53 に近い値だし、あてずっぽうで 53.1 となる…って書いたけど、本当は 53.017 だな。m(_ _)m

数年前までの電子情報の学生さんなら、TI の関数電卓持ってたから「授業で解いて…」というと、結果をすぐに答えてくれる優秀な人がクラスに1人くらい必ずいたけど、最近は BYOD でパソコンを使うので TI の関数電卓持ってないから、解いてくれるヤツいないのよね。