ホーム » スタッフ » 斉藤徹 » 講義録 » 情報構造論 » 再帰呼び出しと再帰方程式

2020年5月
日 月 火 水 木 金 土
 12
3456789
10111213141516
17181920212223
24252627282930
31  

リンク集

検索・リンク

Google Office 365

再帰呼び出しと再帰方程式

投稿者: in 情報構造論, 斉藤徹, 講義録 投稿日:

再帰関数と再帰方程式

再帰関数は、自分自身の処理の中に「問題を小さくした」自分自身の呼び出しを含む関数。プログラムには問題が最小となった時の処理があることで、再帰の繰り返しが止まる。

// 階乗 (末尾再帰)
int fact( int x ) {
   if ( x <= 1 )
      return 1 ;
   else
      return x * fact( x-1 ) ;
}
// ピラミッド体積 (末尾再帰)
int pyra( int x ) {
   if ( x <= 1 )
      return 1 ;
   else
      return x*x + pyra( x-1 ) ;
}
// フィボナッチ数列 (非末尾再帰)
int fib( int x ) {
   if ( x <= 2 )
      return 1 ;
   else
      return fib( x-1 ) + fib( x-2 ) ;
}

これらの関数の結果について考えるとともに、この計算の処理時間を説明する。 最初のfact(),pyra()については、 x=1の時は、関数呼び出し,x<=1,return といった一定の処理時間を要し、 で表せる。 x>1の時は、関数呼び出し,x<=1,*,x-1,returnの処理(Tb)に加え、x-1の値で再帰を実行する処理時間T(N-1)がかかる。 このことから、 で表せる。

} 再帰方程式

このような再帰を使って表した式は再帰方程式と呼ばれる。これを代入によって解けば、一般式  が得られる。

T(1)=Ta
T(2)=Tb+T(1)=Tb+Ta
T(3)=Tb+T(2)=2×Tb+Ta
:
T(N)=Tb+T(N-1)=Tb + (N-2)×Tb+Ta

一般的に、再帰呼び出しプログラムは(考え方に慣れれば)分かりやすくプログラムが書けるが、プログラムを実行する時には、局所変数や関数の戻り先を覚える必要があり、深い再帰ではメモリ使用量が多くなる。
ただし、fact() や pyra() のような関数は、プログラムの末端で再帰が行われている。(fib()は、再帰の一方が末尾ではない)
このような再帰は、末尾再帰と呼ばれ、関数呼び出しの return を、再帰処理の先頭への goto 文に書き換えるといった最適化が可能である。言い換えるならば、末尾再帰の処理は繰り返し処理に書き換えが可能である。このため、末尾再帰の処理をループにすれば再帰のメモリ使用量の問題を克服できる。

再帰を含む一般的なプログラム例

ここまでの再帰方程式は、再帰の度にNの値が1減るものばかりであった。もう少し一般的な再帰呼び出しのプログラムを、再帰方程式で処理時間を分析してみよう。
以下のプログラムを実行したらどんな値になるであろうか？それを踏まえ、処理時間はどのように表現できるであろうか？

int array[ 8 ] = {
  3 , 6 , 9 , 1 , 8 , 2 , 4 , 5 ,
} ;

int sum( int a[] , int L , int R ) { // 非末尾再帰
    if ( R - L == 1 ) {
        return a[ L ] ;
    } else {
        int M = (L + R) / 2 ;
        return sum( a , L , M ) + sum( a , M , R ) ;
    }
}
int main() {
    printf( "%d¥n" , sum( array , 0 , 8 ) ) ;
    return 0 ;
}

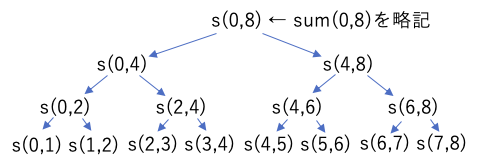
このプログラムでは、配列の合計を計算しているが、引数の L,R は、合計範囲の 左端・右端を表している。そして、再帰のたびに２つに分割して解いている。

このような、処理を分割し、分割したそれぞれを再帰で計算し、その処理結果を組み合わせて最終的な結果を求めるような処理方法を、分割統治法と呼ぶ。

このプログラムでは、対象となるデータ件数(R-L)をNとおいた場合、実行される命令からsum()の処理時間Ts(N)は次の再帰方程式で表せる。

   ← Tβ + (L〜M)の処理時間 + (M〜R)の処理時間

これを代入の繰り返しで解いていくと、

ということで、このプログラムの処理時間は、 で表せる。

再帰方程式の事例として、ハノイの塔の処理時間について説明し、 数学的帰納法での証明を示す。

ハノイの塔


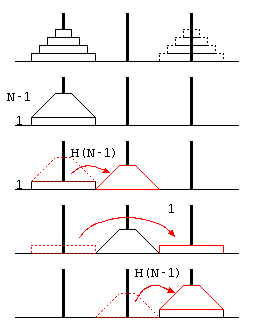
ハノイの塔は、３本の塔にN枚のディスクを積み、(1)1回の移動ではディスクを1枚しか動かせない、(2)ディスクの上により大きいディスクを積まない…という条件で、山積みのディスクを目的の山に移動させるパズル。

一般解の予想

ハノイの塔の移動回数を とした場合、 少ない枚数での回数の考察から、 以下の一般式で表せることが予想できる。

 … ①

この予想が常に正しいことを証明するために、ハノイの塔の処理を、 最も下のディスク1枚と、その上の(N-1)枚のディスクに分けて考える。

再帰方程式

上記右の図より、N枚の移動をするためには、上に重なるN-1枚を移動させる必要があるので、

 … ②
　… ③

ということが言える。(これがハノイの塔の移動回数の再帰方程式)
ディスクが枚の時、予想が正しいのは明らか①,②。
ディスクが 枚で、予想が正しいと仮定すると、 枚では、

　… ③より
 … ①を代入

となり、 枚でも、予想が正しいことが証明された。 よって数学的帰納法により、1枚以上で予想が常に成り立つことが証明できた。

理解度確認

  • 前再帰の「ピラミッドの体積」pyra() を、ループにより計算するプログラムを記述せよ。
  • 前講義での2分探索法のプログラムを、再帰によって記述せよ。(以下のプログラムを参考に)。また、このプログラムの処理時間にふさわしい再帰方程式を示せ。
  • 再帰のフィボナッチ関数 fib() の処理時間にふさわしい再帰方程式を示せ。
int a[ 10 ] = {
   7 , 12 , 22 , 34 , 41 , 56 , 62 , 78 , 81 , 98
} ;
int find( int array[] , int L , int R , int key ) { // 末尾再帰
   // 目的のデータが見つかったら 1,見つからなかったら 0 を返す。
   if ( __________ ) {
      return ____ ; // 見つからなかった
   } else {
      int M = _________ ;
      if ( array[ M ] == key )
         return ____ ;
      else if ( array[ M ] > key )
         return find( array , ___ , ___ , key ) ;
      else
         return find( _____ , ___ , ___ , ___ ) ;
   }
}
int main() {
   if ( find( a , 0 , 10 , 56 ) )
      printf( "みつけた¥n" ) ;
}

再帰を使ったソートアルゴリズム

データを並び替える有名なアルゴリズムの処理時間のオーダは、以下の様になる。

この中で、高速なソートアルゴリズムは、クイックソート(最速のアルゴリズム)とマージソート(オーダでは同程度だが若干効率が悪い)であるが、ここでは、再帰方程式で処理時間をイメージしやすい、マージソートにて説明を行う。

マージソートの分析

マージソートは、与えられたデータを2分割し、 その2つの山をそれぞれマージソートを行う。 この結果の2つの山の頂上から、大きい方を取り出す…という処理を繰り返すことで、 ソートを行う。

このことから、再帰方程式は、以下のようになる。

  • Tm(1)=Ta

この再帰方程式を、N=1,2,4,8…と代入を繰り返していくと、 最終的に処理時間のオーダが となる。




：

よって、

選択法とクイックソートの処理時間の比較

データ数 N = 20 件でソート処理の時間を計測したら、選択法で 10msec 、クイックソートで 20msec であった。

  1. データ件数 N = 100 件では、選択法,クイックソートは、それぞれどの程度の時間がかかるか答えよ。
  2. データ件数何件以上なら、クイックソートの方が高速になるか答えよ。

設問2 は、通常の関数電卓では求まらないので、数値的に方程式を解く機能を持った電卓が必要。

タグ: , , ,