入出力リダイレクト
プログラムの動作を確認する場合、指定された値を使って計算したり、その結果を他のプログラムで使いたい場合が多い。そこで、入出リダイレクトについて説明する。
入力リダイレクト
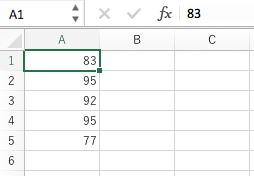
以下に上げるような Excel のデータで平均を計算してみよう。
A6 に =AVERAGE(A1:A5) を入力…
というのは、ナシ。Visual Basic で組むのもナシ。(^_^;
Excelで、「ファイル-名前をつけて保存」、「ファイル形式」に「スペース区切りテキスト(.prn)」で保存する。
// 入力値の平均を求める
// ファイルは、Z:¥foo¥bar¥avg.c にあるとする。
#include <stdio.h>
int main() {
int count = 0 , sum = 0 ;
int x ;
while( scanf( "%d" , &x ) == 1 ) {
count++ ;
sum += x ;
}
printf( "%lf¥n" , sum / count ) ; // この行は間違い。修正せよ。
return 0 ;
}
このプログラムを普通に実行したら、キーボードから 83,95,92,95,77 と毎回入力しなければならない。めんどくさくない?
Excel の空白区切りのデータを読み込む
先程の Excel で保存したファイルを同じディレクトリにコピーする。(Z:¥foo¥bar¥avg.prnとする)
コンパイラで、avg.c をコンパイルし、avg.exe ができていることを確認し、 cmd.exe を起動 Z:¥> cd Z:¥foo¥bar Z:¥foo¥bar> avg.exe < avg.prn
このように、プログラムを起動する時に、通常はキーボードから入力するプログラムに対し、起動時に “< ファイル名” を付けて起動し、ファイル入力に切り替えることを、入力リダイレクトと言う。
出力リダイレクトとグラフ化
前回の授業での sin(x) のプログラムの実行結果を、Excel で確認してみよう。
// sin の値を出力
// ファイルは、Z:¥foo¥bar¥sin.c にあるとする。
#include <stdio.h>
#include <math.h>
int main() {
double th , y ;
for( th = 0.0 ; th <= 360.0 ; th += 5.0 ) {
y = sin( th / 180.0 * 3.1415926535 ) ;
printf( "%lf %lf¥n" , th , y ) ;
}
return 0 ;
}
プログラムを実行する時に、
コンパイラで sin.c をコンパイルし、sin.exe ができていることを確認し cmd.exe を起動 Z:¥> cd Z:¥foo¥bar プログラムのディレクトリに移動 Z:¥foo¥bar> sin.exe > sin.csv プログラムを起動し出力を sin.csv に保存
このように、プログラムを起動する時に、通常は結果を画面に出力するプログラムに対し、起動時に “> ファイル名” を付けて起動し、結果をファイル出力に切り替えることを、出力リダイレクトと言う。
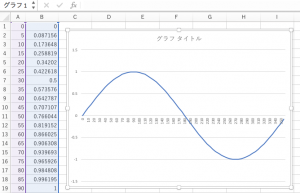
Excelにインポートしてグラフ化
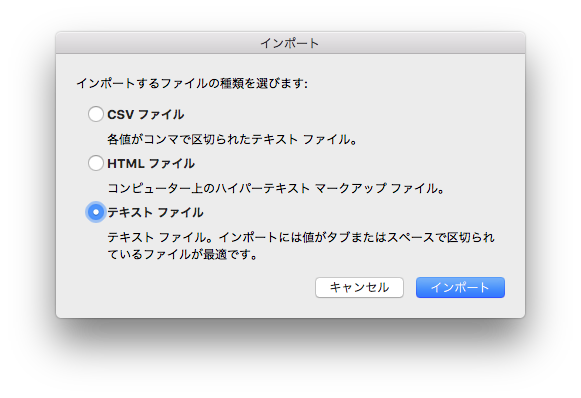
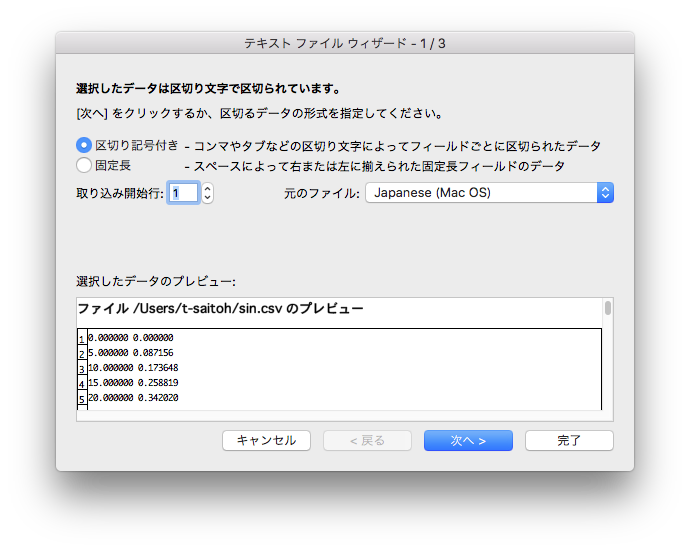
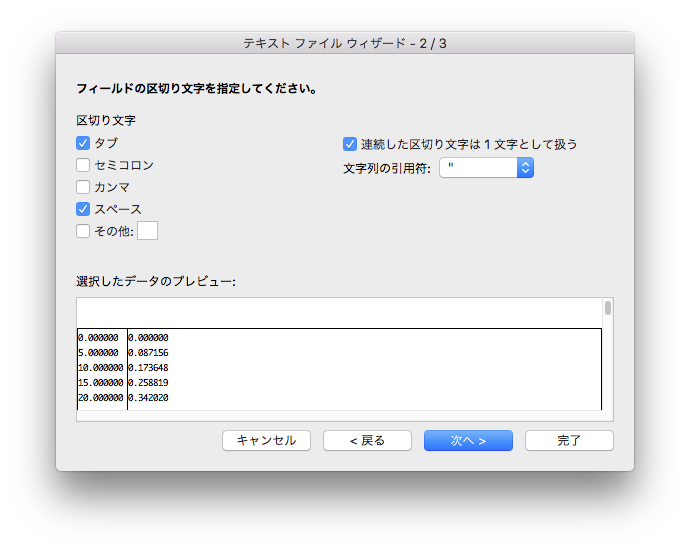
Excel を起動し、「ファイル-インポート」より、「テキストファイル」を選び、「区切り文字」-「スペース区切り」でデータを取り込む。
あとは、取り込まれたデータ範囲を選択し、「挿入」-「グラフ」で好きなグラフ形式を選ぶ。
実数の扱い・レポート-No.1
プログラムの制御構造と実数の取扱いの確認として、以下のレポートを次回講義までに提出せよ。
No.1-1 制御構造
以下の3つ(No.1-1-1,No.1-1-2,No1-1-3)の問題から、No.1-1-「(自分の出席番号 % 3)+1」について、プログラムのフローチャートを描き、その実行順序を20ステップめまで答えよ。
レポートには、
- 元プログラム
- フローチャート
- 実行順序
- 変数の変化がわかる内容
を明記すること。
No.1-1-1
No.1-1-2
switch-case 文は説明していませんが、挙動をよく調べて回答してください。
No.1-1-3
No.1-2 実数の扱い
自分の携帯電話番号(もしくは家の電話番号)の末尾4桁のうち、2桁を整数部、末尾2桁を小数部として、その値を2進数に変換した結果を、計算方法が判るように答えよ。ただし、結果の2進数の小数部は8桁まで答えよ。
例えば、0778628278 ならば、82.78 )10を、xxxxxxx.xxxxxxxx )2 のように答えること。
実数の注意点・回答編
回答がすぐに見えないように、別記事に分ける
数値の精度に注意
// case-1 ---- プログラムが止まらない
#define PI 3.1415926535
int main() {
double th , y ;
// 0〜πまで100分割でsinを求める
for( th = 0.0 ; th != PI ; th += PI / 100.0 ) {
y = sin( th ) ;
printf( "%lf %lf¥n" , th , y ) ;
}
return 0 ;
}
このプログラムの問題点は、終了条件が th != PI で書かれている点。
コンピュータの中では、データはすべて2進数で扱い、データを保存する桁数も有限である。
このため、0.0314159265 を 100 回 加えても、桁末尾の誤差のため、3.14159265 != 3.1415926535となってしまう。(ただしこの説明は10進数で説明しているけど、実際は2進数で同じような現象が発生している。)
int型とdouble型での暗黙の型変換
// case-2 ---- y の値が全てゼロ
int main() {
int th ;
double y ;
for( th = 0 ; th <= 360 ; th += 5 ) {
y = sin( th / 180 * 3.1415926535 ) ;
printf( "%d %lf¥n" , th , y ) ;
}
return 0 ;
}
このプログラムの問題点は、th / 180 。これがゼロになる原因。
コンピュータの中では、整数型 int と、実数 double 型では、計算の仕方が異なる。特に、実数型は、小数点の位置や指数を考えながら計算を行う必要があるため、処理に時間がかかる。このため、大量のデータを扱う場合にはコンピュータにとって簡単な計算となるように書く必要がある。
整数型は、小数点以下の値を持たない。このためコンピュータの中では、th = 5 の時、th / 180 を計算すると、5/180 = 0.0277 ではなく、5/180 = 0 で計算を行う(小数点以下は切り捨て)。
C言語の原則: 暗黙の型変換
同じ精度で計算できるのなら同じ精度の型で計算する。
精度が異なる場合は、精度の高い型に変換してから計算する。
int 演算子 int = int
int 演算子 double = double
このようなことが発生するので、y=sin(th…)の行は、以下のように書くべきである。
y = sin( th / 180.0 * 3.1415926535 ) ; // 180.0 は double 型 y = sin( (double)th / 180 * 3.1415926535 ) ; // 型キャストで double 型 y = sin( double( th ) / 180 * 3.1415926535 ) ; // C++の型変換関数 y = sin( (double)th / 180.0 * 3.1415926535 ) ; // 暗黙の型変換を排除
数値の範囲に注意
// 16bit コンピュータの時代に、
// 画面上のマウスとターゲットの距離を計算したかった
int distance( int x0 , int y0 , int x1 , int y1 ) {
int dx = x1 - x0 ;
int dy = y1 - y0 ;
return sqrt( dx * dx + dy * dy ) ;
}
例えば、このプログラムで (x0,y0)=(0,0) , (x1,y1)=(200,200) 出会った場合、sqrt( 40000 + 40000 ) という計算が出て来る。
ところで、16bit コンピュータにおける int 型は、どうやって覚えているのか?
符号あり整数型
コンピュータの中では、負の数を扱う必要から、2の補数表現が用いられる。
x = 0000,0000,0000,1010(2) = 10(10)
~x = 1111,1111,1111,0101 1の補数
~x + 1 = 1111,1111,1111,0110 1の補数に+1 ⇒ -10(10)
x + ~x = 1111,1111,1111,1111
x + ~x + 1 = 1,0000,0000,0000,0000 ≒ 0 // 16bit目ははみ出るからzero
このため、16bit コンピュータの int 型で扱える数は、
max = 0111,1111,1111,1111(2) = 32767(10) min = 1000,0000,0000,0000(2) = -32768(10)
40000 は、16bit コンピュータでは、扱える範囲を越えている。
ということで、前述のプログラムは、
// 16bit コンピュータなら、long int 型は 32bit
int distance( int x0 , int y0 , int x1 , int y1 ) {
long int dx = x1 - x0 ;
long int dy = y1 - y0 ;
return (int)sqrt( dx * dx + dy * dy ) ;
}
// スピードを気にしないのなら(sqrtがdouble型だし...)
double distance( double x0 , double y0 , double x1 , double y1 ) {
double dx = x1 - x0 ;
double dy = y1 - y0 ;
return sqrt( dx * dx + dy * dy ) ;
}