高専ライブ:2018年4月29日(第572回)
- ゲストのお話
- 球技大会の話
- ゴールデンウィークの話
ゲスト:福井高専卒業生 前田様
担当:西野(2E,MC)、中島(4C,MIX)、水島(4C)、中村(教員)
コンストラクタと複素数クラスと隠蔽化
コンストラクタ
プログラミングでは、データの初期化忘れによる間違いもよく発生する。これを防ぐために、C++ のクラスでは、コンストラクタ(構築子)がある。データ構造の初期化専用の関数。
// コンストラクタ
#include <stdio.h>
#include <string.h>
class Person {
private:
char name[ 20 ] ;
int phone ;
public:
void print() {
printf( "%s %d¥n" , name , phone ) ;
}
Person() { // コンストラクタ(A)
name[0] = '¥0' ; // 空文字列
phone = 0 ;
}
Person( const char str[] , int tel ) { // コンストラクタ(B)
strcpy( name , str ) ;
phone = tel ;
}
~Person() { // デストラクタ
print() ; // 内容の表示
}
} ;
int main() {
Person saitoh( "t-saitoh" , 621111 ) ; // (A)で初期化
Person tomoko() ; // (B)で初期化
saitoh.print() ; // "t-saitoh 621111" の表示
tomoko.print() ; // " 0" の表示
return 0 ; // この時点で saitoh.~Person()
// tomoko.~Person() が自動的に
} // 呼び出される。
コンストラクタと反対に、デストラクタは、データが不要となった時に自動的に呼び出される関数。
複素数クラスの例
隠蔽化と基本的なオブジェクト指向の練習課題として、複素数クラスをあげる。ここでは、複素数の加算・乗算を例に説明をするので、減算・除算などの処理を記述することで、クラスの扱いに慣れてもらう。
直交座標系
#include <stdio.h>
#include <math.h>
class Complex {
private:
double re ; // 実部
double im ; // 虚部
public:
void print() {
printf( "%lf + j%lf¥n" , re , im ) ;
}
Complex( double r , double i ) {
re = r ;
im = i ;
}
Complex() {
re = im = 0.0 ;
}
void add( Complex z ) {
re = re + z.re ;
im = im + z.im ;
}
void mul( Complex z ) {
double r = re * z.re - im * z.im ;
double i = re * z.im + im * z.re ;
re = r ;
im = i ;
}
} ; // ←何度も繰り返すけど、ここのセミコロン忘れないでね
int main() {
Complex a( 1.0 , 2.0 ) ;
Complex b( 2.0 , 3.0 ) ;
a.print() ;
a.add( b ) ;
a.print() ;
a.mul( b ) ;
a.print() ;
}
極座標系
上記の直交座標系の Complex クラスは、加減算の関数は単純だけど、乗除算の関数を書く時には面倒になってくる。この場合、極座標系でプログラムを書いたほうが判りやすいかもしれない。
class Complex {
private:
double r ; // 絶対値 r
double th ; // 偏角 θ
public:
void print() {
printf( "%lf ∠ %lf¥n" , r , th / 3.14159265 * 180.0 ) ;
}
Complex() {
r = th = 0.0 ;
}
Complex( double x , double y ) {
r = sqrt( x*x + y*y ) ;
th = atan2( y , x ) ; // 象限を考慮したatan()
}
void add( Complex z ) {
; // 自分で考えて
}
void mul( Complex z ) { // 極座標系での乗算は
r = r * z.r ; // 絶対値の積
th = th + z.th ; // 偏角の和
}
} ; // ←しつこく繰り返すけど、セミコロン忘れないでね(^_^;
このように、プログラムを開発していると、当初は直交座標系でプログラムを記述していたが、途中で極座標系の方がプログラムが書きやすいという局面となるかもしれない。しかし、オブジェクト指向による隠蔽化を正しく行っていれば、利用者に影響なく「データ構造」や「その手続き(メソッド)」を書換えることも可能となる。
このように、プログラムをさらに良いものとなるべく書換えることは、オブジェクト指向ではリファクタリングと呼ぶ。
再帰処理の処理時間
再帰関数と再帰方程式
再帰関数は、自分自身の処理の中に「問題を小さくした」自分自身の呼び出しを含む関数。プログラムには問題が最小となった時の処理があることで、再帰の繰り返しが止まる。
// 階乗
int fact( int x ) {
if ( x <= 1 )
return 1 ;
else
return x * fact( x-1 ) ;
}
// ピラミッド体積
int pyra( int x ) {
if ( x <= 1 )
return 1 ;
else
return x*x + pyra( x-1 ) ;
}
// フィボナッチ数列
int fib( int x ) {
if ( x <= 2 )
return 1 ;
else
return fib( x-1 ) + fib( x-2 ) ;
}
これらの関数の結果について考えるとともに、この計算の処理時間を説明する。 最初のfact(),pyra()については、 x=1の時は、関数呼び出し,x<=1,return といった一定の処理時間を要し、 で表せる。 x>1の時は、関数呼び出し,x<=1,*,x-1,returnの処理に加え、x-1の値で再帰の処理時間がかかる。 このことから、
で表せる。 これを代入によって解けば、
で表せる。 こういった式は、再帰方程式と呼ばれ、一般式を求めることとなる。
fact() や pyra() のような関数は、プログラムの末端に再帰が行われている。(fib()は、再帰の一方が末尾ではない)
このような再帰は、末尾再帰と呼ばれ、関数呼び出しの return を、再帰処理の先頭への goto 文に最適化が可能である。つまり繰り返し処理に書き換えが可能である。このため、ループにすれば局所変数を消費しない。
最後に、再帰方程式の事例として、ハノイの塔の処理時間について説明し、 数学的帰納法での証明を示す。
ハノイの塔
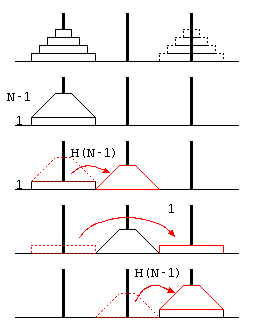
ハノイの塔は、3本の塔にN枚のディスクを積み、ディスクの上により大きいディスクを積まずに、移動させるパズル。
一般解の予想
ハノイの塔の移動回数を とした場合、 少ない枚数での回数の考察から、
ということが予想ができる。
この予想が常に正しいことを証明するために、ハノイの塔の処理を、 最も下のディスク1枚と、その上の(N-1)枚のディスクに分けて考える。
再帰方程式
これより、
ということが言える。
ディスクが枚の時、予想が正しいのは明らか。
ディスクが 枚で、予想が正しいと仮定すると、
枚では、
となり、 枚でも、予想が正しいことが証明された。 よって数学的帰納法により、1枚以上で予想が常に成り立つことが証明できた。
再帰を含む一般的なプログラム例
ここまでの再帰方程式は、再帰の度にNの値が1減るものばかりであった。もう少し一般的なプログラムで再帰方程式を使って処理時間を考えてみよう。
以下のプログラムを実行したらどんな値になるであろうか?それを踏まえ、処理時間はどのように表現できるであろうか?
int array[ 8 ] = {
3 , 6 , 9 , 1 , 8 , 2 , 4 , 5 ,
} ;
int sum( int a[] , int L , int R ) {
if ( R - L == 1 ) {
return a[ L ] ;
} else {
int M = (L + R) / 2 ;
return sum( a , L , M ) + sum( a , M , R ) ;
}
}
int main() {
printf( "%d¥n" , sum( array , 0 , 8 ) ) ;
return 0 ;
}
// s(0,8) ← sum(a,0,8)
// / \
// / \
// s(0,4) s(4,8)
// / \ / \
// s(0,2) s(2,4) s(4,6) s(6,8)
// / \ / \ / \ / \
// s(0,1) s(1,2) s(2,3) s(3,4) s(4,5) s(5,6) s(6,7) s(7,8)
このプログラムでは、配列の合計を計算しているが、引数の L,R は、合計範囲の 左端・右端を表している。そして、再帰のたびに2つに分割して解いている。
このような、処理を分割し、分割した処理を再帰で計算し、その分割した処理結果を組み合わせて結果を求めるような処理方法を、分割統治法と呼ぶ。
このことから、以下の再帰方程式が得られる。
これを、代入法により解いていくと、
ということで、このプログラムの処理時間は、 で表される。
創造工学演習・予備実験(SQLとPHP)
先週のPHPの予備実験に引き続き、データベースの説明とそのプログラムで演習を行う。
<?php
// データの保存先
$dbfile = "/home/guests/guest0/public_data/tsaitoh.db" ;
if ( !file_exists( $dbfile ) ) {
// データベースの宣言と初期化
$db = new SQLite3( $dbfile ) ;
$cmd = "create table nametel ( name char( 20 ) , phone char( 20 ) ) ;"
."insert into nametel ( name , phone ) values ( 't-saitoh' , '090-1111-1111' ) ;"
."insert into nametel ( name , phone ) values ( 'tomoko' , '090-2222-2222' ) ;"
."insert into nametel ( name , phone ) values ( 'mitsuki' , '090-3333-3333' ) ;"
."insert into nametel ( name , phone ) values ( 'ayuka' , '090-4444-4444' ) ;"
;
if ( $db->exec( $cmd ) ) {
print "Success.\n" ;
} else {
print "Fail\n" ;
}
$db = null ;
}
?>
<html>
<head>
<title></title>
</head>
<body>
<?php
// 警告表示の抑止
ini_set( 'error_reporting' , E_WARNING ) ;
// データベース処理(検索処理)
$db = new SQLite3( $dbfile ) ;
$id = $_REQUEST[ "name" ] ;
if ( $db !== FALSE && $id != "" ) {
// SQL命令の生成(インジェクションの危険性指摘は別述)
$cmd = "select * from nametel where name='$id' ;" ;
print $cmd ;
// 問い合わせの実行
$result = $db->query( $cmd ) ;
print "<table border='1'>\n" ;
print "<tr><td>name</td><td>phone</td></tr>" ;
while( ($row = $result->fetchArray( SQLITE3_BOTH )) !== FALSE ) {
print "<tr>"
."<td>".$row[0]."</td>"
."<td>".$row[1]."</td>"
."</tr>\n" ;
}
print "</table>\n" ;
}
?>
<form method="post" action="sql.php">
<input type="text" name="name" />
<input type="submit" value="exec" />
</form>
<?php
// データベース登録処理
$newname = $_REQUEST[ "newname" ] ;
$newphone = $_REQUEST[ "newphone" ] ;
if ( $newname != "" && $newphone != "" ) {
// データ登録用SQL
$cmd = "insert into nametel ( name , phone ) values ( '$newname' , '$newphone' ) ;" ;
// データ登録
$db->exec( $cmd ) ;
print "$newname さんの電話番号 $newphone を登録しました" ;
}
?>
<form method="post" action="sql.php">
<input type="text" name="newname" />
<input type="text" name="newphone" />
<input type="submit" value="exec" />
</form>
</body>
</html>
高専ライブ:2018年4月22日(第571回)
- 新年度の授業の話
- 体力テストの話
- サイエンス共和国傑作選 第4回「天気図を描く話」
- 球技大会の話
担当:越後(2E,MC)、西島(4EI,MIX),椎林(2B)、中村(教員)
実数の注意点
C言語でプログラムを作成していて、簡単な数値計算のプログラムでも動かないと悩んだことはないだろうか?解らなくて友達のプログラムを真似したら動いたけど、なぜ自分のプログラムは動かなかったのか深く考えたことはあるだろうか?
まずは動く例
以下のプログラムは、見れば判るけど、th を 0度〜360度まで5度刻みで変化させながら、y = sin(th) の値を表示するプログラム。
// sin の値を出力
#include <stdio.h>
#include <math.h>
int main() {
double th , y ;
for( th = 0.0 ; th <= 360.0 ; th += 5.0 ) {
y = sin( th / 180.0 * 3.1415926535 ) ;
printf( "%lf %lf¥n" , th , y ) ;
}
return 0 ;
}
動かないプログラム
では、以下のプログラムはどうだろうか?
// case-1 ---- プログラムが止まらない
#define PI 3.1415926535
int main() {
double th , y ;
// 0〜πまで100分割でsinを求める
for( th = 0.0 ; th != PI ; th += PI / 100.0 ) {
y = sin( th ) ;
printf( "%lf %lf¥n" , th , y ) ;
}
return 0 ;
}
// case-2 ---- y の値が全てゼロ
int main() {
int th ;
double y ;
for( th = 0 ; th <= 360 ; th += 5 ) {
y = sin( th / 180 * 3.1415926535 ) ;
printf( "%d %lf¥n" , th , y ) ;
}
return 0 ;
}
どちらも、何気なく読んでいると、動かない理由が判らないと思う。そして、元のプログラムと見比べながら、case-1 では、「!=」を「<=」に書き換えたり、case-2 では、「int th ;」を「double th ;」に書き換えたら動き出す。
では何が悪かったのか…
回答編
数値の範囲に注意
前節の回答編で示したが、数値の扱える値の範囲に注意すべきである。
私自身が自分で書いたプログラムで悩んだ例を以下に示す。
// 16bit コンピュータの時代に、
// 画面上のマウスとターゲットの距離を計算したかった
int distance( int x0 , int y0 , int x1 , int y1 ) {
int dx = x1 - x0 ;
int dy = y1 - y0 ;
return sqrt( dx * dx + dy * dy ) ;
}
このプログラムを実行した時、通常はうまく動くのだけど、時々「sqrt は、負の値では計算できません」というエラーを表示する。
なぜだろうか?
回答編
2進数への変換(補助資料)
10進数で 123.45 は、1*102 + 2*101 + 3*100 + 4*10-1 + 5*10-2 を意味する。(あたりまえ)
2進数に変換する場合、整数部と小数部に分けて考えると、
10進数なら、それぞれを 10 で割る、10 をかけると 123 / 10 = 12.3 小数部に3 が出てくる。 0.45 * 10 = 4.5 整数部に4 が出てくる。 2進数なら、それぞれを 2 で割る、2をかけると...
123.45 を 2進数に変換 2)123 )10 = 1111011 )2  ̄ ̄ ̄ ̄ 2) 61 ... 1 次々と2で割って、余りを求める  ̄ ̄ ̄ ̄ 2) 30 ... 1  ̄ ̄ ̄ ̄ 2) 15 ... 0  ̄ ̄ ̄ ̄ 2) 7 ... 1  ̄ ̄ ̄ ̄ 2) 3 ... 1  ̄ ̄ ̄ ̄ 2) 1 ... 1  ̄ ̄ ̄ ̄ 0 ... 1 ✕2)0.45 )10 = 0.01110011001100...)2  ̄ ̄ ̄ ̄ ̄ ✕2)0.9 ... 0 次々と2倍して、整数部を求める  ̄ ̄ ̄ ̄ ̄ ✕2)1.8 ... 1 ※  ̄ ̄ ̄ ̄ ̄ ✕2)1.6 ... 1  ̄ ̄ ̄ ̄ ̄ ✕2)1.2 ... 1  ̄ ̄ ̄ ̄ ̄ ✕2)0.4 ... 0  ̄ ̄ ̄ ̄ ̄ ✕2)0.8 ... 0 ※の繰り返し  ̄ ̄ ̄ ̄ ̄ ✕2)1.6 ... 1  ̄ ̄ ̄ ̄ ̄ : よって、123.45 )10 = 1111011 .011100110011...)2
大域変数・局所変数・スコープ
繰り返しが動かない例
#include <stdio.h>
int i ;
void foo() { // foo() は 3個Aを表示するプログラム。
for( i = 0 ; i < 3 ; i++ )
printf( "A" ) ;
}
int main() {
foo() ;
return 0 ;
}
では、
#include <stdio.h>
int i ;
void foo() { // foo() は 3個Aを表示するプログラム。
for( i = 0 ; i < 3 ; i++ )
printf( "A" ) ;
}
int main() {
// A はいくつ表示される?
for( i = 0 ; i < 3 ; i++ )
foo() ;
return 0 ;
}
大域変数と局所変数
編集中:もう少し加筆予定
引数渡しと構造体からオブジェクト指向へ
値渡し、ポインタ渡し、参照渡し
構造体の使い方の話では、関数との構造体のデータ渡しでポインタなどが出てくるので、 値渡し・ポインタ渡し・参照渡しの復習。(参照渡しはC++で導入された考え方)
値渡し
C言語の基本は、値渡し。呼び出し側の実引数は、関数側の仮引数に値がコピーされる。 このため、呼び出し側の変数(下の例ではa)の中身は変化しない。 よって、関数の呼び出しで呼び出し側の変数が勝手に中身が変わらないので、予想外の変数の中身の変化が無く分かりやすい。
// 値渡し(call by value)の例
void foo( int x ) {
x++ ;
printf( "%d¥n" , x ) ;
}
void main() {
int a = 123 ;
foo( a ) ; // 124が表示
foo( a ) ; // 124が表示
}
ポインタ渡し
しかし、上の例では、foo()の呼び出しで、変数aの中身が変化してくれたほうが都合が良い場合もある。 この場合は、C言語ではポインタを使って記述する。 このように、関数を呼び出して、手元の変数が変化することは、副作用と呼ばれる。 副作用の多いプログラムは、変数の値の管理がわかりにくくなるので、副作用は最小限に記述すべき。
// ポインタ渡し(call by pointer)の例
void foo( int *px ) {
(*px)++ ;
printf( "%d¥n" , (*px) ) ;
}
void main() {
int a = 123 ;
foo( &a ) ; // 124が表示
foo( &a ) ; // 125が表示
}
参照渡し
しかし、ポインタを多用すると、ポインタを動かしてトラブルも増えることから、ポインタはあまり使わない方が良い。 そこで、C++では参照型というものがでてきた。
// 参照型(call by reference)の場合
void foo( int &x ) {
x++ ;
printf( "%d¥n" , x ) ;
}
void main() {
int a = 123 ;
foo( a ) ; // 124が表示
foo( a ) ; // 125が表示
}
参照型は、ポインタを使っていないように見えるけれども、機械語レベルでみればポインタを使ったものと同じ。
構造体でオブジェクト指向もどき
例えば、名前と電話番号の構造体で処理を記述する場合、 以下の様な記載を行うことで、データ設計者とデータ利用者で分けて 仕事ができることを説明。
// この部分はデータ構造の設計者が書く // データ構造を記述 struct Person { char name[10] ; int phone ; } ; // データに対する処理を記述 void readPerson( struct Person* p ) { // ポインタの参照で表記 scanf( "%s%d" , (*p).name , &(*p).phone ) ; } void printPerson( struct Person* p ) { // アロー演算子で表記 printf( "%s %d¥n" , p->name , p->phone ) ; } // この部分は、データ利用者が書く int main() { // Personの中身を知らなくてもいいから配列を定義(データ隠蔽) struct Person table[ 10 ] ; for( int i = 0 ; i < 10 ; i++ ) { // 入力して、出力する...という雰囲気で書ける(手続き隠蔽) readPerson( &table[i] ) ; printPerson( &table[i] ) ; } return 0 ; }
このプログラムの書き方では、mainの中を読むだけもで、 データ入力とデータ出力を行うことはある程度理解できる。 この時、データ構造の中身を知らなくてもプログラムが理解でき、 データ実装者はプログラムを記述できる。これをデータ構造の隠蔽化という。 一方、readPerson()や、printPerson()という関数の中身についても、 入力・出力の方法をどうするのか知らなくても、 関数名から動作は推測できプログラムも書ける。 これを手続きの隠蔽化という。
C++のクラスで表現
上記のプログラムをそのままC++に書き直すと以下のようになる。
#include <stdio.h> // この部分はクラス設計者が書く class Person { private: // クラス外からアクセスできない部分 // データ構造を記述 char name[10] ; // メンバーの宣言 int phone ; public: // クラス外から使える部分 // データに対する処理を記述 void read() { // メソッドの宣言 // pのように対象のオブジェクトを明記する必要はない。 scanf( "%s%d" , name , &phone ) ; } void print() { printf( "%s %d¥n" , name , phone ) ; } } ; // ← 注意ここのセミコロンを書き忘れないこと。 // この部分はクラス利用者が書く int main() { Person table[ 10 ] ; for( int i = 0 ; i < 10 ; i++ ) { table[i].read() ; // メソッドの呼び出し table[i].print() ; // オブジェクト.メソッド() } // 文法エラーの例 printf( "%d¥n" , table[0].phone ) ; // phoneはprivateなので参照できない。 return 0 ; }
用語の解説:C++のプログラムでは、データ構造とデータの処理を、並行しながら記述する。 データ構造に対する処理は、メソッド(method)と呼ばれる。 データ構造とメソッドを同時に記載したものは、クラス(class)と呼ぶ。 そのclassに対し、具体的な値や記憶域が割り当てられたものをオブジェクト(object)と呼ぶ。
制御構文について
プログラムの基本は、処理の順序を正しく理解していること。
まずは理解度確認
では、過去の電子情報3年プログラム応用のテスト問題から、以下のプログラムの実行順序を答えて下さい。
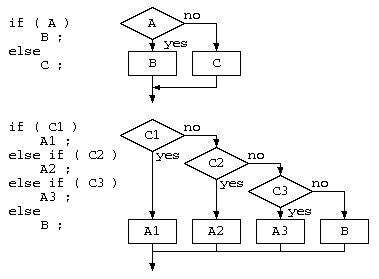
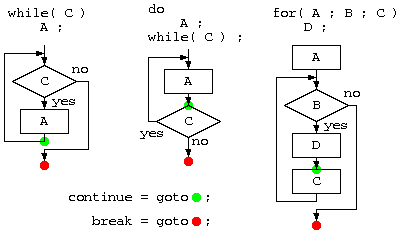
制御構文とフローチャート
構文の入れ子
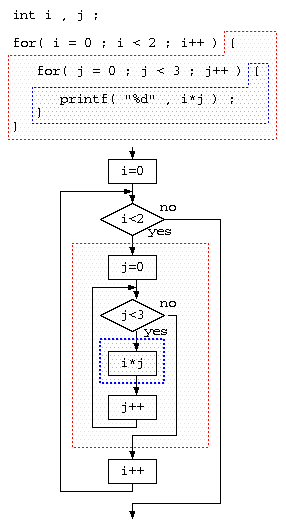
繰り返し処理とオーダ記法
先週に、単純繰り返し処理の時間分析をやったので、次のステップに。
2分探索法の処理時間
データを探す処理において、単純検索より速い方法ということで、2分探索法の処理速度見積もりを行う。
// 2分探索法 O(log N) int a[ 1000 ] ; int size ; // データ数 N int L = 0 ; // L=下限のデータの場所 int R = size ; // R=上限のデータ+1の場所 while( L != R ) { int M = (L + R) / 2 ; // 計算は整数型で行われることに注意 if ( a[M] == key ) // 見つかった break ; else if ( a[M] < key ) // |L |M. |R L = M + 1 ; // |----------|-+---------| else // |L---------|M| R = M ; // |M+1------|R }
上記のようなプログラムの場合、処理に要する時T(N)は、
# Mは繰り返し回数
処理は、対象となるデータ件数が繰り返し毎に半分となり、対象データ件数が1件になれば処理が終わる。このことから、
となることから、 の関係が成り立つ。よって、
は、以下のように表せる。
単純なソート(最大選択法)の処理時間
次に、並べ替え処理の処理時間について考える。
int a[ 1000 ] ;
int size ;
for( int i = 0 ; i < size - 1 ; i++ ) {
int tmp ;
// i..size-1 の範囲で一番大きいデータの場所を探す
int m = i ;
for( int j = i + 1 ; j < size ; j++ ) {
if ( a[j] > a[m] )
m = j ;
}
// 一番大きいデータを先頭に移動
tmp = a[i] ;
a[i] = a[m] ;
a[m] = tmp ;
}
このプログラムの処理時間T(N)は…
となる。
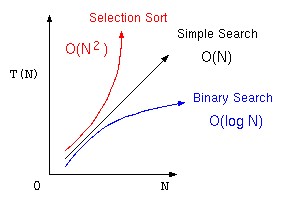
オーダー記法
ここまでのアルゴリズムをまとめると、処理時間に大きく影響する部分は、赤字の部分であり、特にその項の係数は、コンピュータの処理性能に影響を受けるが、アルゴリズムの優劣を考える場合は、それぞれ、
の部分の方が重要である。
| 単純サーチ | |
| 2分探索法 | |
| 最大選択法 |
そこで、アルゴリズムの優劣を議論する場合は、この処理時間の見積もりに最も影響する項で、コンピュータの性能によって決まる係数を除いた部分を抽出した式で表現する。これをオーダー記法と言う。
| 単純サーチ | オーダーNのアルゴリズム | |
| 2分探索法 | オーダー log N のアルゴリズム | |
| 最大選択法 | オーダー N2 のアルゴリズム |
練習問題
- コンピュータで2分探索法で、データ100件で10[μsec]かかったとする。
データ10000件なら何[sec]かかるか? の処理時間を要するアルゴリズムを、オーダー記法で書くとどうなるか?また、このようなアルゴリズムの例を答えよ。
の処理時間を要するアルゴリズムを、オーダー記法で書くとどうなるか?