先週に、単純繰り返し処理の時間分析をやったので、次のステップに。

2分探索法の処理時間

データを探す処理において、単純検索より速い方法ということで、2分探索法の処理速度見積もりを行う。

// 2分探索法　O(log N)
int a[ 1000 ] ;
int size ;      // データ数 N
int L = 0 ;     // L=下限のデータの場所
int R = size ;  // R=上限のデータ+1の場所
while( L != R ) {
   int M = (L + R) / 2 ;  // 計算は整数型で行われることに注意
   if ( a[M] == key )     // 見つかった
      break ;
   else if ( a[M] < key ) // |L         |M.         |R
      L = M + 1 ;         // |----------|-+---------|
   else                   // |L---------|M|
      R = M ;             //              |M+1------|R
}

上記のようなプログラムの場合、処理に要する時T(N)は、

　# Mは繰り返し回数

処理は、対象となるデータ件数が繰り返し毎に半分となり、対象データ件数が1件になれば処理が終わる。このことから、

となることから、 の関係が成り立つ。よって、は、以下のように表せる。

単純なソート(最大選択法)の処理時間

次に、並べ替え処理の処理時間について考える。

int a[ 1000 ] ;
int size ;

for( int i = 0 ; i < size - 1 ; i++ ) {
    int tmp ;
    // i..size-1 の範囲で一番大きいデータの場所を探す
    int m = i ;
    for( int j = i + 1 ; j < size ; j++ ) {
        if ( a[j] > a[m] )
            m = j ;
    }
    // 一番大きいデータを先頭に移動
    tmp = a[i] ;
    a[i] = a[m] ;
    a[m] = tmp ;
}

このプログラムの処理時間T(N)は…

となる。

オーダー記法

ここまでのアルゴリズムをまとめると、処理時間に大きく影響する部分は、赤字の部分であり、特にその項の係数は、コンピュータの処理性能に影響を受けるが、アルゴリズムの優劣を考える場合は、それぞれ、 の部分の方が重要である。

単純サーチ
２分探索法
最大選択法

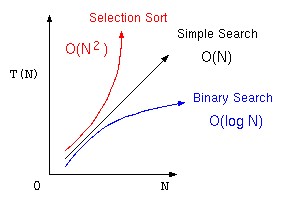
そこで、アルゴリズムの優劣を議論する場合は、この処理時間の見積もりに最も影響する項で、コンピュータの性能によって決まる係数を除いた部分を抽出した式で表現する。これをオーダー記法と言う。

単純サーチ		オーダーNのアルゴリズム
2分探索法		オーダー log N のアルゴリズム
最大選択法		オーダー N2 のアルゴリズム

練習問題

1. コンピュータで2分探索法で、データ100件で10[μsec]かかったとする。
   データ10000件なら何[sec]かかるか？
2. の処理時間を要するアルゴリズムを、オーダー記法で書くとどうなるか？また、このようなアルゴリズムの例を答えよ。
3. の処理時間を要するアルゴリズムを、オーダー記法で書くとどうなるか？