2分木とヒープ
前期最後の双方向リストの次ということで、2分木の説明を行う。

最初に2分探索法について説明をして、検索処理速度のオーダーが、 で示されることを復習する。 その後、この方法が配列でランダムアクセスが可能で、a[(l+r)/2] が取り出せる からこそ有効であることを説明する。
これを踏まえ、2分木のイメージ図を示した後、ノード(節)とパス(枝)といった用語を説明し、 構造体の宣言を示してから、この概念を説明する。 ひとまず、処理の理解ということで、データ生成と検索処理までを示す。
struct Tree {
int data ;
struct Tree* left ;
struct Tree* right ;
} ;
struct Tree* tcons( int x , struct Tree*l , struct Tree*r ) {
struct Tree* ans ;
ans = (struct Tree*)malloc( sizeof( struct Tree ) ) ;
if ( ans != NULL ) {
ans->data = x ;
ans->left = l ;
ans->right = r ;
}
return ans ;
}
// データは、0..100の値と仮定し、見つからなかったら負
int find( struct Tree* p , int key ) {
while( p != NULL ) {
if ( p->data == key )
return key ;
else if ( p->data > key )
p = p->left ;
else
p = p->right ;
}
return -1 ;
}
void main() {
struct Tree* top =
tcons( 50 , tcons( 24 , NULL , NULL ) ,
tcons( 76 , NULL , NULL ) ) ;
printf( "%d\n" , find( top , 20 ) ) ;
}
この2分木構造では、木の段数がM段あって、木が左右均一であれば、 全データ件数は、 の関係から、
を満たし、処理時間は、
で示される。
ヒープ
2分木の欠点を考えると、データ1件につき、左右のポインタが必要であることから、 32bit コンピュータであれば、sizeof( struct Tree ) は12byte となり、単純な配列1件=4byte と比べればメモリのムダとなる。
この欠点の改善方法として、ヒープと呼ばれる方法がある。
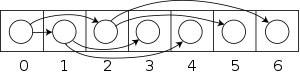
図出典Wikipedia
この方法であれば、N番目のデータの左枝は2*N+1、右枝は2*N+2の位置に存在するため、 ポインタが不要となる。