ホーム » スタッフ » 斉藤徹 » 講義録 » 情報構造論 » スタックと待ち行列

スタックと待ち行列

投稿者: in 情報構造論, 斉藤徹, 講義録 投稿日:

計算処理中に一時的なデータの保存として、stackとqueueがよく利用されるが、それを配列を使って記述したり、任意の大きさにできるリストを用いて記述する。

# 授業は、前回の演習時間が不十分だったので、前半講義、後半演習時間。

スタック

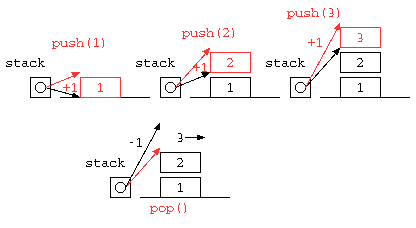
一時的な値の記憶によく利用されるスタックは、一般的にLIFO( Last In First out )と呼ばれる。配列を使って記述すると以下のようになるであろう。

#define STACK_SIZE 32
int stack[ STACK_SIZE ] ;
int sp = 0 ;

void push( int x ) {
    stack[ sp++ ] = x ;
}
int pop() {
    return stack[ --sp ] ;
}
void main() {
    push( 1 ) ; push( 2 ) ; push( 3 ) ;
    printf( "%d\n" , pop() ) ; // 3
    printf( "%d\n" , pop() ) ; // 2
    printf( "%d\n" , pop() ) ; // 1
}

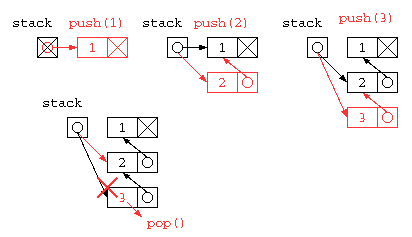
しかし、この中にSTACK_SIZE以上のデータは貯えられない。同じ処理をリストを使って記述すれば、ヒープメモリを使い切るまで使うことができるだろう。

struct List* stack = NULL ;

void push( int x ) {
    stack = cons( x , stack ) ;
}
int pop() {
    int ans = stack->data ;
    struct List* d = stack ;
    stack = stack->next ;
    free( d ) ;
    return ans ;
}

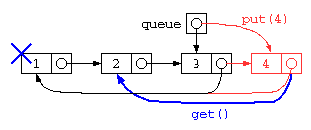
キュー(QUEUE)

２つの処理の間でデータを受け渡す際に、その間に入って一時的にデータを蓄えるためには、待ち行列(キュー)がよく利用される。 FIFO(First In First Out)

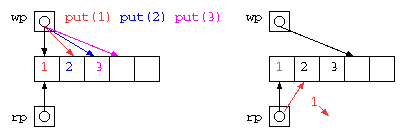
配列にデータを入れる場所(wp)と取り出す場所のポインタ(rp)を使って蓄えれば良いが、配列サイズを超えることができないので、データを取り出したあとの場所を循環して用いるリングバッファは以下のようなコードで示される。

#define QUEUE_SIZE 32
int queue[ QUEUE_SIZE ] ;
int wp = 0 ;
int rp = 0 ;

void put( int x ) {
    queue[ wp++ ] = x ;
    if ( wp >= QUEUE_SIZE )
        wp = 0 ;
}
int get() {
    int ans = queue[ rp++ ] ;
    if ( rp >= QUEUE_SIZE )
        rp = 0 ;
    return ans ;
}
void main() {
    put( 1 ) ; put( 2 ) ; put( 3 ) ;
    printf( "%d\n" , get() ) ; // 1
    printf( "%d\n" , get() ) ; // 2
    printf( "%d\n" , get() ) ; // 3
}

このようなデータ構造も、get() の実行が滞るようであれば、wp が rp に循環して追いついてしまう。
そこで、このプログラムもリストを使って記述すると以下のようになる。

struct List* queue = NULL ;
struct List** tail = &queue ;

void put( int x ) {
    *tail = cons( x , NULL ) ;
    tail = &( (*tail)->next ) ;
}
int get() {
    int ans = queue->data ;
    struct List* d = queue ;
    queue = queue->next ;
    free( d ) ;
    return ans ;
}

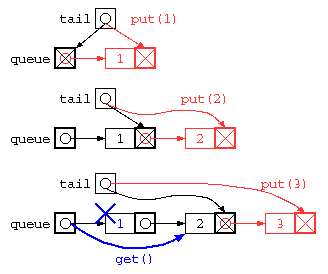
ただし、上記のプログラムは、データ格納後にget()で全データを取り出してしまうと、tail ポインタが正しい位置になっていないため、おかしな状態になってしまう。
また、このプログラムでは、rp,wp の2つのポインタで管理することになるが、 2重管理を防ぐために、リストの先頭と末尾を1つのセルで管理する循環リストが使われることが多い。

理解確認

  • 配列を用いたスタック・待ち行列は、どのような処理か？図などを用いて説明せよ。
  • リスト構造を用いたスタック・待ち行列について、図などを用いて説明せよ。
  • スタックや待ち行列を、配列でなくリスト構造を用いることで、どういう利点があるか？欠点があるか説明せよ。

タグ: , , ,