繰り返し処理と処理時間の見積もり

単純サーチの処理時間

ここで、プログラムの実行時間を細かく分析してみる。

// ((case-1))
// 単純サーチ O(N)
#include <stdio.h>

int main() {
    int a[ 10 ] = {
        12 , 64 , 35 , 29 , 59 , 9 , 83 , 73 , 21 , 61
    } ;
    int N = 10 ;  // 実際のデータ数(Nとする)
    int key = 21 ;   // 探すデータ
    for( int i = 0 ; i < N ; i++ )
        if ( a[i] == key )
            break ;
    return 0 ;
}

import java.util.*;

public class Main {
    public static void main(String[] args) throws Exception {
        // Your code here!
        int a[] = {
            12 , 64 , 35 , 29 , 59 , 9 , 83 , 73 , 21 , 61
        } ;
        int N = a.length ;
        int key = 21 ;
        for( int i = 0 ; i < N ; i++ )
            if( a[i] == key )
                break ;
    }
}

例えばこの単純サーチをフローチャートで表せば、以下のように表せるだろう。フローチャートの各部の実行回数は、途中で見つかる場合があるので、最小の場合・最大の場合を考え平均をとってみる。また、その１つ１つの処理は、コンピュータで機械語で動くわけだから、処理時間を要する。この時間を ${T_{\tiny A}$ , ${T_{\tiny B}$ , ${T_{\tiny C}$ , ${T_{\tiny D}$ とする。

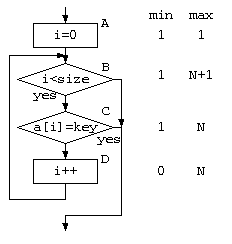
この検索処理全体の時間 ${T(N)}$ を考えると、平均時間とすれば、以下のように表せるだろう。

$T(N)=T_A+T_B+T_B\times\frac{N}{2}+T_C+T_C\times\frac{N-1}{2}+T_D\times\frac{N}{2}$

$T(N)=T_A+T_B+\frac{T_C}{2}+\frac{N}{2}\times(T_B+T_C+T_D)$

$T(N)=T_{\alpha}+N\times{T_{\beta}}$

ここで例題

この単純サーチのプログラムを動かしてみたら、N=1000で、5μ秒かかったとする。では、N=10000であれば、何秒かかるだろうか？

感のいい学生であれば、直感的に 50μ秒と答えるだろうが、では、T_β,T_α は何秒だったのだろうか？上記のT(N)=T_α+N ✕ T_β に当てはめると、N=1000,T(N)=5μ秒の条件では、連立方程式は解けない。

ここで一番のポイントは、データ処理では N が小さな値の場合(データ件数が少ない状態)はあまり考えない。N が巨大な値であれば、T_αは、1000T_βに比べれば微々たる値という点である。よって

$\red{T(N)\simeq{N\times{T_{\beta}}}}$

で考えれば良い。これであれば、T(1000)=5μ秒=T_β×1000 よって、T_β=5n秒となる。この結果、T(10000)=T_β×10000=50μ秒となる。

2分探索法と処理時間

次に、単純サーチよりは、速く・プログラムとしては難しくなった方法として、2分探索法の処理時間を考える。データはあらかじめ昇順に並べておくことで、一度の比較で対象件数を減らすことで高速に探すことができる。

下記プログラムを読む場合の注意点：

Lは、探索範囲の一番左端のデータのある場所。

Rは、探索範囲の一番右端のデータのある場所 + 1

// ((case-2))
// 2分探索法 O(log N)
#include <stdio.h>

int main() {
    int a[] = {
        9 , 12 , 21 , 29 , 35 , 59 , 61 , 64 , 73 , 83
    } ;
    int L =  0 ; // L : 左端のデータの場所
    int R = 10 ; // R : 右端のデータの場所+1 
    while( L != R ) {
        int M = (L + R) / 2 ;
        if ( a[M] == key )
            break ;
        else if ( a[M] < key )
            L = M + 1 ;
        else
            R = M ;
    }
    return 0 ;
}

import java.util.*;

public class Main {
    public static void main(String[] args) throws Exception {
        int a[] = {
            9 , 12 , 21 , 29 , 35 , 59 , 61 , 64 , 73 , 83
        } ;
        int L = 0 ;        // L : 左端のデータの場所
        int R = a.length ; // R : 右端のデータの場所+1
        int key = 73 ;
        while( L != R ) {
            int M = (L + R) / 2 ;
            if ( a[M] == key )
                break ;
            else if ( a[M] < key )
                L = M + 1 ;
            else
                R = M ;
        }
    }
}

このプログラムでは、1回のループ毎に対象となるデータ件数は、 $\frac{N-1}{2}$ となる。説明を簡単にするために1回毎にN/2件となると考えれば、M回ループ後は、 $\frac{N}{2^M}$ 件となる。データ件数が1件になれば、データは必ず見つかることから、以下の式が成り立つ。

$\frac{N}{2^M}=1$

$N=2^M$ …両辺のlogをとる

$\log_2{N}=M$

2分探索は、繰り返し処理であるから、処理時間は、

$T(N)=T_{\alpha}+M\times{T_{\beta}}$ … (Mはループ回数)

$T(N)=T_{\alpha}+\log{N}\times{T_{\beta}}$

ここで、本来なら log の底は2であるが、後の見積もりの例では、問題に応じて底変換の公式 ( $\log_{2}{N} = \log_{10}{N} / \log_{10}{2}$ )で係数が出てくるが、これはT_βに含めて考えればいい。

単純なソート(選択法)の処理時間

次に、並べ替え処理の処理時間について考える。

単純な並べ替えアルゴリズムとしてはバブルソートなどもあるが、2重ループの内側のループ回数がデータによって変わるので、選択法で考える。

// ((case-3))
// 選択法 O(N^2)
#include <stdio.h>

int main() {
    int a[] = {
        12 , 64 , 35 , 29 , 59 , 9 , 83 , 73 , 21 , 61
    } ;
    int size = 10 ;
    for( int i = 0 ; i < size - 1 ; i++ ) {
        int tmp ;
        // i..size-1 の範囲で一番大きいデータの場所を探す
        int m = i ;
        for( int j = i + 1 ; j < size ; j++ ) {
            if ( a[j] > a[m] )
                m = j ;
        }
        // 一番大きいデータを先頭に移動
        tmp = a[i] ;
        a[i] = a[m] ;
        a[m] = tmp ;
    }
    return 0 ;
}

import java.util.*;

public class Main {
    public static void main(String[] args) throws Exception {
        int a[] = {
            12 , 64 , 35 , 29 , 59 , 9 , 83 , 73 , 21 , 61
        } ;
        int size = a.length ;
        for( int i = 0 ; i < size - 1 ; i++ ) {
            int tmp ;
            int m = i ;
            for( int j = i + 1 ; j < size ; j++ ) {
                if ( a[j] > a[m] )
                    m = j ;
            }
            tmp = a[i] ;
            a[i] = a[m] ;
            a[m] = tmp ;
        }
    }
}

このプログラムの処理時間T(N)は…

$T(N)=T_{\alpha}$

$+T_{\beta}+T_{\gamma}\times(N-1)$ … i=0の時
$+T_{\beta}+T_{\gamma}\times(N-2)$ … i=1の時
:
$+T_{\beta}+T_{\gamma}\times 1$ … i=N-1の時

$T(N)=T_{\alpha}+\sum_{\footnotesize{i=1}}^{\footnotesize{N-1}}(T_{\beta}+T_{\gamma}\times{i})$ …(参考数列の和の公式)

$T(N)=T_{\alpha}+(N-1){\times}T_{\beta}+T_{\gamma}\times\frac{N(N-1)}{2}$

$T(N)=T_A+N{\times}T_B+N^{2}\times{T_C}$

となる。

オーダー記法

ここまでのアルゴリズムをまとめると以下の表のようになる。ここで処理時間に大きく影響する部分は、最後の項の部分であり、特にその項の係数 ${T_{\beta},T_{\gamma}}$ は、コンピュータの処理性能に影響を受けるが、アルゴリズムの優劣を考える場合は、それぞれ、 ${N,\log{N},N^2$ の部分の方が重要である。

単純サーチ	${T(N)}=T_{\alpha}+$ $\red{T_{\beta}\times{N}}$
２分探索法	${T(N)}=T_{\alpha}+$ $\red{T_{\beta}\times\log{N}}$
最大選択法	${T(N)}=T_{\alpha}+T_{\beta}\times{N}+$ $\red{T_{\gamma}\times{N^2}}$

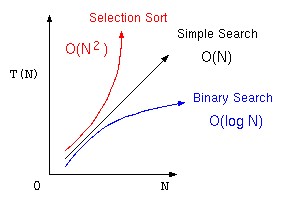
そこで、アルゴリズムの優劣を議論する場合は、この処理時間の見積もりに最も影響する項で、コンピュータの性能によって決まる係数を除いた部分を取り除いた式で表現する。これをオーダー記法と言う。

単純サーチ	${O(N)}$	オーダーNのアルゴリズム
2分探索法	${O(\log{N})}$	オーダー log N のアルゴリズム
最大選択法	${O(N^2)}$	オーダー N² のアルゴリズム

練習問題

ある処理のデータ数Nに対する処理時間が、 ${T(N)}=T_a + T_b \times N^2+T_c \times 2^N$ であった場合、オーダー記法で書くとどうなるか？
コンピュータで2分探索法で、データ100件で10[μsec]かかったとする。
データ10000件なら何[sec]かかるか？
(ヒント: 底変換の公式)
${T(N)}=T_A$ の処理時間を要するアルゴリズム(データ件数が変わっても処理時間は一定)を、オーダー記法で書くとどうなるか？また、このような処理時間となるアルゴリズムの例を答えよ。
${T(N)}=T_A+T_B\times\sqrt{N}+T_C\times\log{N}$ の処理時間を要するアルゴリズムを、オーダー記法で書くとどうなるか？
(ヒント: ロピタルの定理)

2と4の解説
1は、N→∞において、N²≪ 2^Nなので、O(2^N) 。厳密に回答するなら、練習問題4と同様の証明が必要。
3は、O(1)。
- 誤答の例：O(0)と書いちゃうと、T(N)=T_α×0=0になってしまう。
- 事例は、電話番号を、巨大配列の”電話番号”番目の場所に記憶するといった方法。(これはハッシュ法で改めて講義予定)

日	月	火	水	木	金	土
		1	2	3	4	5
6	7	8	9	10	11	12
13	14	15	16	17	18	19
20	21	22	23	24	25	26
27	28	29	30