ホーム » スタッフ » 斉藤徹 » 講義録 » 情報制御基礎 » 移動平均の処理

2023年7月
日 月 火 水 木 金 土
 1
2345678
9101112131415
16171819202122
23242526272829
3031  

リンク集

検索・リンク

Google Office 365

移動平均の処理

投稿者: in 情報制御基礎, 斉藤徹, 講義録 投稿日:

前回の授業で説明したようなA/D変換した数値データを読み取った場合、どのようなことが発生するか考える。

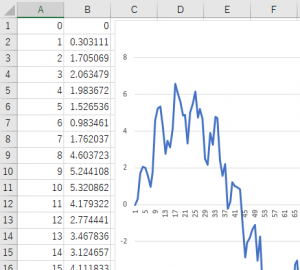
例えば、以下に示すような測定値があったとする。

このデータの一部をグラフ化してみると、次のような波形であった。

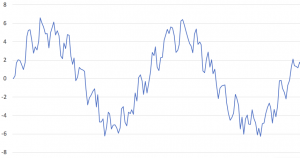
この波形をみると、大きく見ればsinカーブだが、細かい点を見るとデータにブレがある。

誤差の原因

このような測定結果が得られた場合、本来コンピュータで処理したいデータは何であろうか？

原因は様々なものが考えられるが、

  1. 回路のノイズ対策が不十分で、外部の電気的な影響が混入。
    オシロスコープで周期を図ると、60Hz なら、交流電源だったり…
  2. D/A 変換を行う場合には、量子化誤差かもしれない。

例えば、最初の波形が、加速度センサーの値であったとして、船の上で揺れているために、大きな周期で加速度が変化しているかもしれない。一方で、船自体がエンジンによる揺れで加速度が変化しているかもしれない。

船の中で波の揺れと、エンジンの揺れが観測されている加速度センサーの情報で、船の揺れの大きさ・揺れの周期を知りたい場合、どうすればいいだろうか？

移動平均を計算してみる

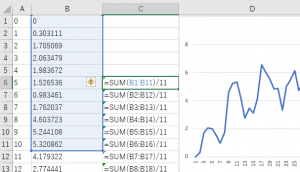
このデータを見ると、10個のデータまでの間で、波形が上下に変動している。船の揺れとエンジンの揺れが原因であれば、10個ぐらいのデータのゆらぎが、エンジンによる揺れと考えられる。では、この10個ぐらいの範囲で値が上下の影響を減らしたければ、どうすればいいか？一番簡単な方法は、前後10個のデータで平均を取ればいいだろう。増減する値を加えれば、プラスの部分とマイナスの部分の値が相殺されて０に近くはず。そこでは、Excel で前後データの平均をとってみよう。

Excelで前後11点の平均を求める式をセルに入れる

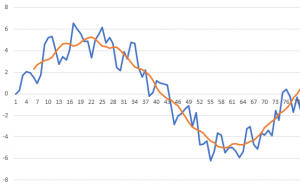
青線：元波形データ(B列)、赤線：前後11点の平均(C列)

このように、データの前後の決められた範囲の平均を平均する処理は、移動平均(単純移動平均)と呼ぶ。

時間tにおけるデータをとした場合、前後5点の移動平均は、以下のような式で表せるだろう。

単純移動平均

単純移動平均は、時刻ｔの平均を、その前後のデータで平均を求めた。この方式は、実際には与えられた波形のデータを全部記録した後に、単純移動平均をとる場合に有効である。

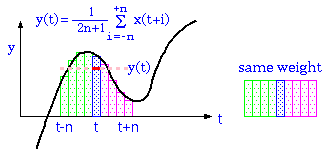
しかし、時々刻々変化する測定値の平均をその都度使うことを考えると、上記の方法は、未来の測定値を使っていることから、現実的ではない。

// 単純移動平均(未来の値も使う)
#define NS 3
int x[ SIZE ] ; // 入力値
int y[ SIZE ] ; // 出力値
for( int t = NS ; t < SIZE-NS ; t++ ) {
   int s = 0 ;
   for( int i = -NS ; i <= +NS ; i++ ) // 2*NS+1回の繰り返し
      s += x[t+i] ;
   y[t] = s / (2*NS + 1) ;
}

過去の値だけを使った移動平均

そこで、過去の値だけで移動平均をとることも考えられる。

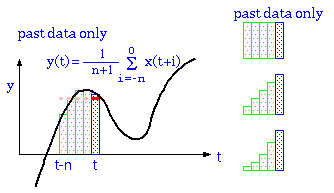
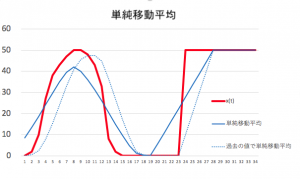
この、単純移動平均と、過去の値だけを使う単純移動平均を、適当な測定値に対して適用した場合のグラフの変化を Excel によってシミュレーションした結果を以下に示す。

しかし、このグラフを見ると、波形後半の部分に注目するとよく分かるが、過去の値だけを使った移動平均では、測定値が立ち上がったのを追いかけて値が増えていく。これでは移動平均は時間的な遅れとなってしまう。

// 未来の値を使わない単純移動平均
for( int t = NS ; t < SIZE ; t++ ) {
   int s = 0 ;
   for( int i = 0 ; i <= NS ; i++ ) // NS+1回の繰り返し
      s += x[t-i] ;
   y[t] = s / (NS+1) ;
}こ

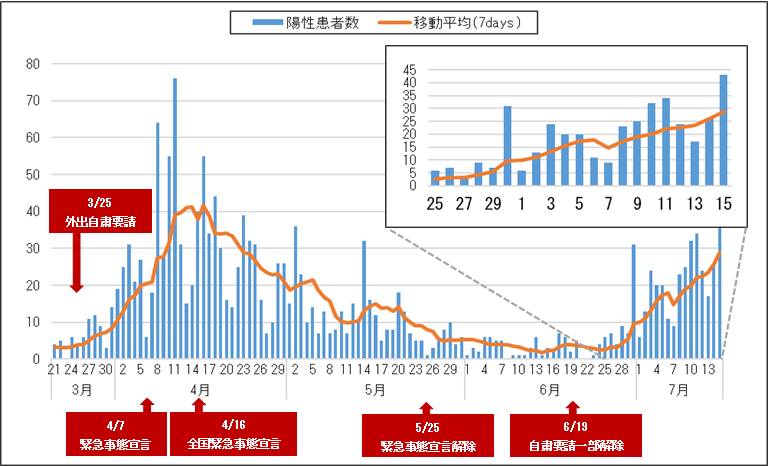
コロナ感染者数のデータの見せ方

昨年までは、コロナ感染者数の増減のグラフを見る機会が多かった。例えば、以下のようなグラフ(神奈川県のデータを引用)を見ると、新規感染者数は青の棒グラフで示されている。しかし、土日の検査が月曜に計上されたりするため、青の棒グラフは週ごとに増減があって分かりにくいため、移動平均の値が合わせてオレンジ色の折れ線グラフで表示されている。しかし、オレンジ色のグラフは、青のグラフより少し右にずれていると思いませんか？

これは、移動平均といっても過去7日間の平均をグラフ化しているため、数日分だけ右にずれているように見えている。ずれが無いように見せたいのなら、3日前から3日後のデータの移動平均であれば、ずれは無くなると思われる。

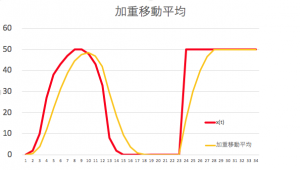
加重移動平均

過去の値を使った移動平均では遅れが発生する。でも、平均を取る際に、「n回前の値」と「現在の値」を考えた時、「その瞬間の平均値」は「現在の値」の方が近い値のはず。であれば、平均を取る時に、「ｎ回前の値は少なめ」「現在の値は多め」に比重をかけて加算する方法がある。

for( int t = 3 ; t < SIZE ; t++ ) {
   // 数個の移動平均だし、
   // ループを使わずに書いてみる。 
   int s = x[t]   * 3   // 現在の値は大きい重み
         + x[t-1] * 2   // 1つ前の値
         + x[t-2] * 1 ; // 2つ前の値(重みは最小)
   y[t] = s / (3+2+1) ;
}

この様に、過去に遡るにつれ、平均をとる比重を直線的に小さくしながら移動平均をとる方法は、加重移動平均と呼ばれる。以下にその変化をExcelでシミュレーションしたものを示す。

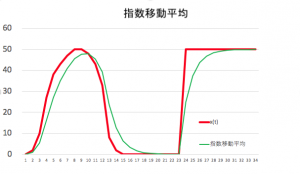
指数移動平均

ここまで説明してきた、単純移動平均や、加重移動平均は、平均をとる範囲の「過去の値」を記憶しておく必要がある。広い時間にわたる移動平均をとる場合は、それに応じてメモリも必要となる。これは、組み込み型の小型コンピュータであれば、メモリが足りず平均処理ができない場合もでてくる。

そこで、荷重移動平均の重みを、は、100%,は50%,は25%… というように、過去に遡るにつれ、半分にして平均をとる。

しかし、以降の項で、 を使うと以下のように書き換えることができる。

// 指数移動平均は、プログラムがシンプル
//  １つ前の平均y[t-1]を覚えるだけでいい。
for( int t = 1 ; t < SIZE ; t++ ) {
   y[t] = ( x[t] + y[t-1] ) / 2 ;
}

この方法であれば、直前の平均値を記録しておくだけで良い。このような移動平均を、指数移動平均と呼ぶ。

ここで示した指数移動平均は、過去を遡るにつれとなっているが、これをさらに一般化した指数移動平均は、以下の式で示される。前述の移動平均は、とみなすことができる。

#define ALPHA 0.5
for( int t = 1 ; t < SIZE ; t++ ) {
    y[t] = ALPHA * x[t] + (1.0 - ALPHA) * y[t-1] ;
}

以下のプログラムは、うまく動かない。理由を説明せよ。

#define RVA 4
for( int t = 1 ; t < SIZE ; t++ ) {
   // 以下はy[t]は全部ゼロになる。
   y[t] = 1/RVA * x[t] + (1.0 - 1/RVA) * y[t-1] ;

   // 以下は、整数型演算だけで、正しく動くだろう。
   // y[t] = ( x[t] + (RVA-1) * y[t-1] ) / RVA ;
}

理解度確認のための小レポート

上記の移動平均の理解のために、以下の資料(講義では印刷資料を配布)の表の中を、電卓などを使って計算せよ。
計算したら、その結果をグラフの中にプロットし、どういった波形となるか確認し、レポートとして提出すること。

この課題は、こちらの Teams フォルダに提出してください。

タグ: , ,