表計算ソフトの使い方(絶対参照・相対参照)
今日の表計算ソフトを使った演習では、下記のサンプルファイルを練習に使うので、Teamsで参照してください。
前回課題の答え合わせ
前回のレポートでは、sin(83度)(例)といった数値の有効数字を考えるというものを考えてもらったので、この有効数字をどう記載すべきか考えてみる。
課題を示す Excel ファイルでは、75度~89度あたりの角度で出題をするようにしてあった。注意しないといけない点は、sinは90度に近づくほど、1に近づく。このため、0.99…といった数値が求まるが、角度がちょっと変化しても、0.99といった部分はほぼ変化しない。だから、83が有効数字2桁ということで、0.99 といった有効数字2桁の書き方では、ちょっと不十分かもしれない。
そこで、83度(有効数字2桁)が小数点以下を丸められた数値と仮定する。この場合、元の数値は 82.5度~83.5度 の可能性がある。これらの値のsinを計算すると、0.9914から0.9935の間であり、小数点以下3桁目は、1~3 の値であり、結果を 0.992 (有効数字3桁) と記載しても良いかもしれない。
sin(82.5°) = 0.991444861 sin(83.0°) = 0.992546152 sin(83.5°) = 0.993571856
表計算ソフトの使い方
情報制御基礎では、プログラムで計算する所を、Excel のような表計算ソフトを用いて検証してもらったりする予定なので、Excel で計算式を使う方法を説明する。
セルの場所と簡単な式
簡単な、品名・単価・個数・価格の表を考える。以下の表のように、列の名前と、品名・単価・個数まで入力した後、単価と個数をかけた価格を求めるとする。
Excel では、表の列には左から、A,B,C,D… , 表の行には上から1,2,3,4,5 と番号が振られていて、特定の列・特定の行のデータを表す時には、列行を組み合わせ、A1に品名、B3に¥80、C5に4 が入っている。
例えば、D2 に、ノート単価120円、ノート個数3個をかけた値を入れたい場合は、D2の場所に、
=B2*C2
を書き込めば、その場所には360が表示される。
先頭の”=”を入力した後、該当する”B2″の場所をクリックするなりカーソルを操作すると、カーソルのセルの場所”B2″が自動的に入力される。さらに”*”を入力した後、”C2″の場所をクリックすれば”C2″が入力される。
Excelでは、入力する文字列の先頭が”=”の場合は、残り部分は計算式として扱われる。
D3には、”=B3*C3″を入力すれば、160 が表示される。しかし、この様な式を何度も入力するのは面倒である。
この場合、セル・カーソルを、D2 に合わせ、[右ボタン]-[コピー]を行い、D3 で[右ボタン]-[貼り付けオプション]-[貼り付け]を行えば、”=B3*C3″が入力される。
ここで注意しないといけないのが、式を張り付ける場合には、貼り付け先のセルの場所が一つ下の行なので、行番号を表す2の部分が1つ下の行番号3に書き換えられて、貼り付けが行われる。(相対参照)
関数式
例えば、下左図のような、数字とその平方根の表を作る場合、A2 に 1、B2に =sqrt( A2 ) を入力、A3 に =A2+1 を入力したあと、B2の式をB3にコピー&ペーストし、A3,B3 を A4~A6にペーストすればいい。
B2に入力したような、sqrt( A2 ) のようなものは、関数式と呼ばれる。
また、A3,B3 といった複数の行・列をまとめた範囲を示す時は、A3:B3 といった表記方法であらわす。
絶対参照と相対参照
最初の例に戻って、単価と個数の積で今度は税率を加えて計算する例を考える。また、税率は後で変化するかもしれないので、B1 のセルに税率を記入しておく場合を考える。
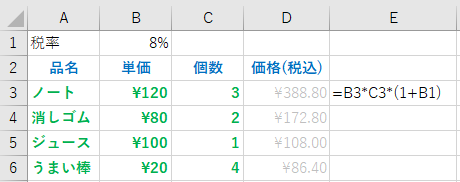
この場合、D3 には、” =B3*C3*(1+B1) ” を入力すればいい。
ただ、このように式を入力すると、D3 の計算式を、D4,D5,D6 にコピーすると、セル D4 には =B4*C4*(1+B2) が入力されてしまい、B2 には単価という文字が記載されているため、正しい結果が求まらない。
こういった場合には、絶対参照を用いる。D3 に記入する式を
=B3*C3*(1+$B$2)
とし、この D3 の式を D4 にコピー&ペーストすると、列記号、行番号の前に$がついた部分の式は、貼り付け場所に応じて変化しない。
このような、$B$2 といったセルの参照は、絶対参照と呼ぶ。これに対し、B2 といったセル参照は、貼り付け場所に応じて書き換えられるので、相対参照と呼ぶ。
絶対参照と相対参照が混ざった、$B2, B$2 といった書き方もある。
式の入力時に[F4ボタン]を押す度に、B2→$B$2→B$2→$B2→B2 と変化する$B2 は、式をコピー&ペーストすると列部分はBのまま、行部分は場所に合わせて変化する。
B$2 は、式をコピー&ペーストすると列部分は場所に合わせて変化し、行部分は2のままとなる。
レポート課題(第5回)
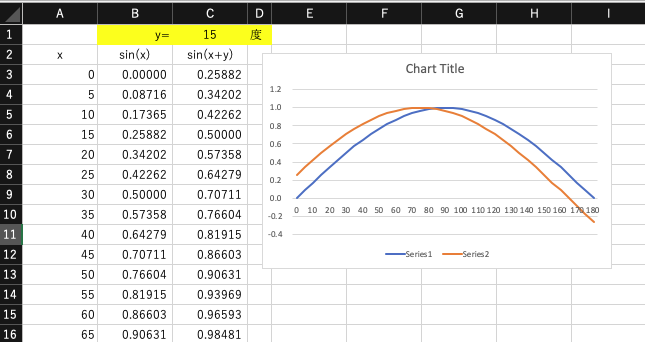
Excel で、xを0〜180度まで変化させたときのsin(x),位相をyとした時のsin(x+y)の値の表を作り、グラフ機能で表示せよ。A列は角度・B列はsin(x)・C列はsin(x+y)の値とし、yの値は”C1″に保存されているものとする。
この時、計算式の入力をどのように行なったのか(相対参照や絶対参照をどのように使ったのか)説明を、グラフの下に入力欄を設け記入せよ。
なお、Excel の sin() 関数は、引数がラジアンで入力する必要があるので、計算式には注意せよ。
そして出来上がった Excel のファイルを、Teams のこちらのフォルダに提出せよ。
実数の取り扱いと誤差
実数型(float / double)
実数型は、単精度実数(float型)と、倍精度実数(double型)があり、それぞれ32bit,64bitでデータを扱う。
指数表現は、大きい値や小さい値を表現する場合に使われ、物理などで1.2345×10-4といった、仮数×基数指数で表現する方法。数学や物理では基数に10を用いるが、コンピュータの世界では基数を2とすることが多い。
単精度型(float)では、符号1bit,指数部8bit,仮数部23bitで値を覚え、数値としては、以下の値を意味する。
符号✕ 1.仮数部 ✕ 2(指数数部-127)
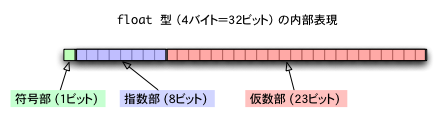
符号部は、正の値なら0, 負の値なら1 を用いる。
仮数部が23bitなので、有効桁(正しい桁の幅)は10進数で約7桁となる。(1.2345678 と 1.2345679 は区別できない)
例えば、float型で扱える最大数は、以下のようになる。
0,1111,1110,111,1111,1111,1111,1111,1111 = 1.1111…×2127 ≒ 2128 ≒ 1038
指数部が1111,1111は、桁あふれで無限大になった値を表す特殊な数字として扱われるので、値として有効な指数部は1111,1110 となっている。
float 型は、計算精度が低いので 通常の数値計算のプログラミングではあまり使われることはない。一方で、ゲームなどの3次元座標計算などでは、精度は必要もないことから、GPU(グラフィックス専用のプロセッサ)では float 型を使うことも多い。また、最近の機械学習のプログラミングでは、神経の動きをまねた計算(ニューラルネットワークプログラミング)が行われるが、これも精度はあまり高くなくてもいいので float 型を使うことも多く、グラフィックス用の GPU で float 型で機械学習の計算を行うことも多い。
倍精度型(double)では、符号1bit,指数部11bit,仮数部52bitで値を覚え、数値としては、以下の意味を持つ。
符号✕ 1.仮数部 ✕ 2(指数部-1023)

これらの実数で計算を行うときには、0.00000001011×210といった値の時に、仮数部に0が並んだ状態を覚えると、計算の精度が低くなるので、1.01100000000×22のように指数部の値を調整して小数点の位置を補正しながら行われる。
double型の場合、52bit=10進数16桁相当の有効桁、最大数で、1.1111…×21023≒10308
倍精度型を使えば、正しく計算できるようになるかもしれないが、実数型はただの加算でも仮数部の小数点の位置を合わせたりする処理が必要で、浮動小数点専用の計算機能を持っていないような、ワンチップコンピュータでは整数型にくらべると10倍以上遅い場合もある。
実数の注意点
C言語でプログラムを作成していて、簡単な数値計算のプログラムでも動かないと悩んだことはないだろうか?解らなくて友達のプログラムを真似したら動いたけど、なぜ自分のプログラムは動かなかったのか深く考えたことはあるだろうか?
単純な合計と平均
整数を入力し、最後に合計と平均を出力するプログラムを以下に示す。
しかし、C言語でこのプログラムを動かすと、10,10,20,-1 と入力すると、合計(sum)40,件数(cnt)3で、平均は13と表示され、13.33333 とはならない。
小数点以下も正しく表示するには、どうすればいいだろうか?
ただし、変数の型宣言を “double data,sum,cnt ;” に変更しないものとする。
// 入力値の合計と平均を求める。
#include <stdio.h>
int main() {
int data ;
int sum = 0 ;
int cnt = 0 ;
for(;;) {
printf( "数字を入力せよ。-1で終了¥n" ) ;
scanf( "%d" , &data ) ;
if ( data < 0 )
break ;
cnt = cnt + 1 ;
sum = sum + data ;
}
printf( "合計 %d¥n" , sum ) ;
printf( "平均 %d¥n" , sum / cnt ) ;
}
C言語では、int型のsum / int型のcnt の計算は、int 型で計算を行う(小数点以下は切り捨てられる)。このため、割り算だけ実数で行いたい場合は、以下のように書かないといけない。
printf( "平均 %lf¥n" , (double)sum / (double)cnt ) ;
// (double)式 は、sum を一時的に実数型にするための型キャスト
まずは動く例
以下のプログラムは、見れば判るけど、th を 0度〜360度まで5度刻みで変化させながら、y = sin(th) の値を表示するプログラム。
// sin の値を出力
#include <stdio.h>
#include <math.h>
int main() {
double th , y ;
for( th = 0.0 ; th <= 360.0 ; th += 5.0 ) {
y = sin( th / 180.0 * 3.1415926535 ) ;
printf( "%lf %lf¥n" , th , y ) ;
}
return 0 ;
}
動かないプログラム
では、以下のプログラムはどうだろうか?
// case-1 ---- プログラムが止まらない
#define PI 3.1415926535
int main() {
double th , y ;
// 0〜πまで100分割でsinを求める
for( th = 0.0 ; th != PI ; th += PI / 100.0 ) {
y = sin( th ) ;
printf( "%lf %lf¥n" , th , y ) ;
}
return 0 ;
}
// case-2 ---- y の値が全てゼロ
int main() {
int th ;
double y ;
for( th = 0 ; th <= 360 ; th += 5 ) {
y = sin( th / 180 * 3.1415926535 ) ;
printf( "%d %lf¥n" , th , y ) ;
}
return 0 ;
}
どちらも、何気なく読んでいると、動かない理由が判らないと思う。そして、元のプログラムと見比べながら、case-1 では、「!=」を「<=」に書き換えたり、case-2 では、「int th ;」を「double th ;」に書き換えたら動き出す。
では何が悪かったのか…
回答編
数値と誤差
コンピュータで計算すると、計算結果はすべて正しいと勘違いをしている人も多い。ここで、改めて誤差について考える。特に、計器で測定した値であれば、測定値自体に誤差が含まれている。
こういった誤差が含まれる数字を扱う場合注意が必要である。例えば実験値を手書きで記録する場合、12.3 と 12.300 では意味が異なる。測定値であやふやな桁を丸めたのであれば、前者は 12.2500〜12.3499… の間の値であり有効数字3桁である。後者は、12.2995〜12.300499… の間の値であり、有効数字5桁である。このため、誤差が含まれる数字の加算・減算・乗算・除算では注意が必要である。
加減乗除算の場合
加減算であれば小数点の位置を揃え、誤差が含まれる桁は有効桁に含めてはいけない。

上記の計算では、0.4567の0.0567の部分は意味がないデータとなる。(情報落ち)
乗除算であれば、有効桁の少ない値と有効桁の多い値の計算では、有効桁の少ない方の誤差の影響が計算結果に出てくるため、通常は、有効桁5桁と2桁の計算であれば、乗除算結果は少ない2桁で書くべきである。

桁落ち
有効桁が大きい結果でも、減算が含まれる場合は注意が必要である。
例えば、以下のような計算では、有効桁7桁どうしでも、計算結果の有効桁は3桁となる。

このような現象は、桁落ちと呼ばれる。
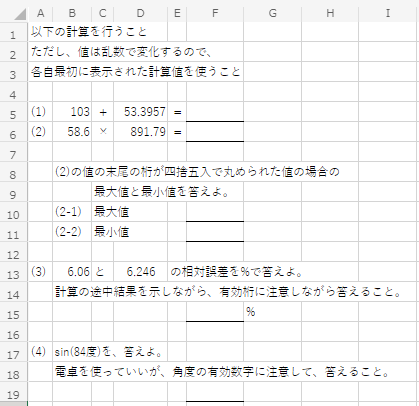
演習問題(4回目)
こちらのフォルダに示す、Excel の表で、有効桁を考えてもらうための演習問題(ランダムに値が作られます)を有効数字を考えながら計算し、答えをレポートにまとめてください。例を以下に示す。
レポートは、こちらのひな型をベースに作成し(手書きノートをキャプチャした資料でもOKです)、同じフォルダに提出してください。
プログラム言語(C言語)の基礎
学際科目の情報制御基礎において、学科間でプログラミングの初歩の理解差があるので、簡単なC言語プログラミングの基礎の説明。
Hello World
“Hello World”と表示するだけのC言語プログラムは以下のようになる。
// コメントの書き方1 // "//"で始まる行は、プログラムの説明(コメント)
/* コメントの書き方2 */ // "/*"から"*/"で囲まれる範囲もコメント
#include <stdio.h> // #で始まる行はプリプロセッサ行
// stdio.h には、入出力関数の説明が書いてある
int main() { // 一連の処理の塊を関数と呼ぶ。
// C言語では main() 関数を最初に実行する。
printf( "Hello World\n" ) ; // printf() は、以下の物を表示する関数。
// "\n"は、文字を出力して改行するための特殊文字
return 0 ; // main() 関数が、正常終了したことを意味する
} // 0 を返り値として返す。
“#include <…>“のプリプロセッサ行は、最初のうちは解りにくいので、「これを書かないとダメ…」と思っていればいい。
#include <stdio.h> は、別ファイル(ヘッダファイル) stdio.h に記載されているプログラムリストを読み込む機能。
stdio.h には、printf() や scanf() などの基本的な関数や定数などの情報が記載されている。
C言語の基本的な命令(文)は、”;”で終わる。(単文)
複数の処理をまとめる場合には、”{“から”}”の中に、複数の文を書き並べる。(複文)
関数とは、複数の処理をひとまとめにした、処理の「かたまり」と思えばいい。
関数の型 関数名( 仮引数 ... ) { 処理1 ... ; 処理2 ... ; }printf() の 文字列中の”\n”(あるいは”¥n”)は、改行を意味する。
「\:バックスラッシュ」は、日本語環境では「¥:円記号」で入力・表示することが多い。
Paiza.io で動かしてみよう
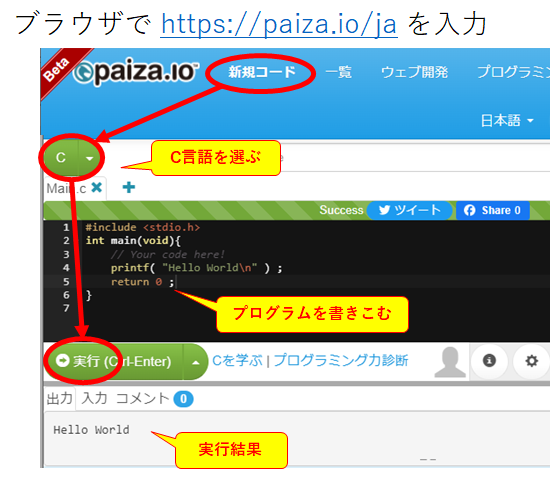
C言語を本格的に使いたいなら、Microsoft Visual Studio などをインストールして使う方が便利だが、情報制御基礎で説明する程度のプログラムなら、Paiza.io が便利。ブラウザの画面で簡単にプログラムの動作を確認することができる。https://paiza.io/jaにアクセスして、上述の Hello World を動かしてみよう。
変数と代入
#include <stdio.h>
#include <math.h> // 数学関数を使う 平方根 sqrt() を使っている
int main() {
// 変数の宣言
int i ; // 符号付き32bit変数 i の宣言
int a = 123 , j ; // a を 123 で初期化 , j も整数型
float x ; // 単精度実数の x を宣言
double y = 1.234 , z ; // 倍精度実数の y を宣言し 1.234 で初期化,
// z も倍精度実数
// 変数への代入
i = 1 ; // i に 1 を代入
i = 12 + 2 * a ; // 12+2*a を代入 a は123なので、
// iには、258 が入る。
x = sqrt( 2.0 ) ; // x に 2.0 の平方根(1.4142)を代入
z = y * 2.0 + x * 3.0 ; // y*2+x*3をzに代入
// 変数の内容の表示
printf( "%d\n" , i ) ; // 整数型(%d)で、 i の値を表示
printf( "%f\n" , x ) ; // 単精度実数(%f) で、x の値を表示
printf( "%lf\n" , z ) ; // 倍精度実数(%lf)で、z の値を表示
printf( "iの値は%d,xの値は%lfです。\n" , i , x ) ;
return 0 ; // 正常終了 0 を返す
}
変数(計算結果を格納する入れ物)を使う場合は、変数を宣言する。
変数名には、何が入っているのか理解しやすいように、名前をつければいい。(英字で始まり、英数字が続くもの,_が入ってもいい)
変数に値を記憶する時は、”変数名=式 ;”の様に書くと、代入演算子”=” の右辺を計算し、その計算結果が左辺の変数に保存される。
変数の内容を表示する時には、printf() の文字列の中に、%d,%f,%lf などの表示したい式の型に応じたものを書いておく。%d=int型 , %f=float型 , %lf=double型
式の値が、その %.. の部分に書き込まれて、出力される。
繰り返しの制御命令
最も基礎的な繰り返し命令として、for() 文を説明。
#include <stdio.h>
int main() {
int i ;
for( i = 1 ; i <= 10 ; i++ ) { // iを1から10まで変化させる。
printf( "%d %d\n" , i , i*i ) ; // i と iの二乗を表示
}
return 0 ;
}
for文の意味を説明するために、対応するフローチャートを示す。
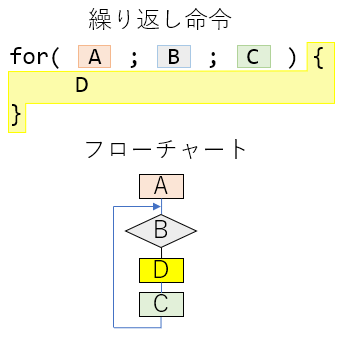
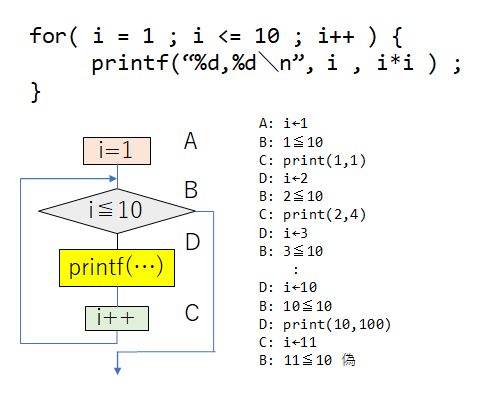
先のプログラムをフローチャートで示し、その命令の実行順序と、その変数の変化を下図に示す。
練習問題1
簡単なプログラミングの練習として、前回講義の練習問題をC言語で書いてみよう。
- 電気電子工学科,電子情報工学科の学生は、出席番号が奇数は処理C,偶数は処理Dについて回答せよ。
- それ以外の学科の学生は、出席番号が奇数は処理A,偶数は処理Bの結果について回答せよ。
- 自分が考えたプログラムは、前述の Paiza.io や、自分のパソコンのC言語環境で入力し、動作結果も確認せよ。
制御構文とフローチャート
構文の入れ子
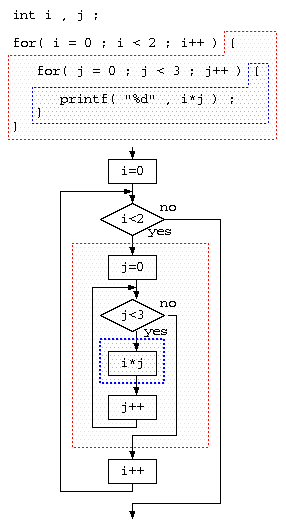
文と複文
C言語の文法で、{,} は複数の処理を連続して実行し、複文とよばれる。複数ので文を構成する。
これに対して、a = 123 ; といったセミコロンで終わる「処理 ;」は単文といい、1つの式で文となる。
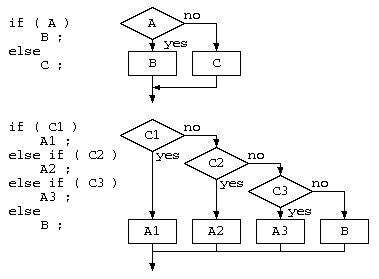
制御構文のif文は、「if ( 条件 ) 文真」で文となる。このため条件が満たされたときに実行する文真が単文であれば、{,} は不要である。条件が満たされない場合の処理も記述するときには、「if ( 条件 ) 文真 else 文偽」を使う。
// if文
if ( 条件 ) {
a = 123 ;
}
if ( 条件 )
a = 123 ; // 単文なら中括弧は不要
// if-then-else
if ( x >= 60 ) {
printf( "合格点\n" ) ;
} else {
printf( "不合格点\n" ) ;
}
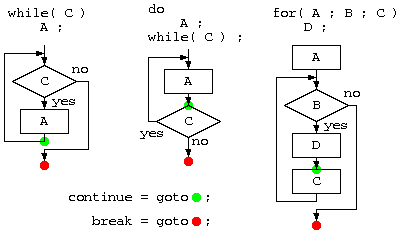
同じように、「while(条件) 文」、「for(A,B,C) 文」、「do 文 while(条件) ;」も、それぞれ文を構成する。
{,} の複文は、{ 文 文 文… } のように、一連の文を実行し、それを1つの文として扱うための機能である。
// while 文
i = 0 ;
while( i < 10 ) {
printf( "%d\n" , i ) ;
i++ ;
}
// for 文
for( i = 0 ; i < 10 ; i++ ) {
printf( "%d\n" , i ) ;
}
// do-while 文
i = 0 ;
do {
printf( "%d\n" , i ) ;
i++ ;
} while( i < 10 ) ;
練習問題2
プログラムの制御構造の確認として、以下の3つ(No.1,No.2,No.3)の問題から、
M科,C科,B科の学生は((自分の出席番号+1) % 2)+1 の問題、E科,EI科の学生は、((自分の出席番号+1) % 3)+1について、プログラムのフローチャートを描き、その処理がどのように進むのか答えよ。
レポートには、以下の点を記載すること。
- フローチャート
- 実行順序と変数の変化がわかる内容
- (できれば、実際にプログラムを動かし、正しいことを検証すること)
// No.1 ---------------------------------------------------------
#include <stdio.h>
int main() {
int i , j ;
for( i = 1 ; i <= 4 ; i++ ) {
if ( i % 2 == 0 ) { // i%2 は2で割った余り,i%2==0ならば偶数のとき
for( j = 1 ; j <= 2 ; j++ )
printf( "%d %d\n" , i , j ) ;
}
}
return 0 ;
}
// No.2 ---------------------------------------------------------
#include <stdio.h>
int main() {
int x = 10 , y = 7 , s = 0 ;
while( x > 0 ) {
if ( x % 2 != 0 )
s = s + y ;
y = y * 2 ;
x = x / 2 ; // 注意: xは整数型
}
printf( "%d\n" , s ) ;
return 0 ;
}
// No.3 ---------------------------------------------------------
#include <stdio.h>
int a[ 6 ] = { 2 , 3 , 5 , 8 , 13 , 21 } ;
int main() {
int left = 0 , right = 6 , mid ;
int key = 13 ;
while( right - left > 0 ) {
mid = (left + right) / 2 ; // 整数型で計算
printf( "%d\n" , a[ mid ] ) ;
if ( a[ mid ] == key )
break ;
else if ( a[ mid ] > key )
right = mid ;
else
left = mid + 1 ;
}
return 0 ;
}
フローチャートと整数型
学際科目の情報制御基礎において、プログラムの基本としてフローチャートと基本的な処理を説明し、数値型の注意点を説明。
フローチャートの基本
プログラムの処理の順序を理解するには、初心者であればフローチャート(流れ図)を使う。
処理の1つ1つを箱で表し、流れを箱の間の矢印で示すことでアルゴリズム(プログラムの考え方)や処理順序を表現する。処理単位の箱は、命令の種類によって箱の書き方が決まっている。
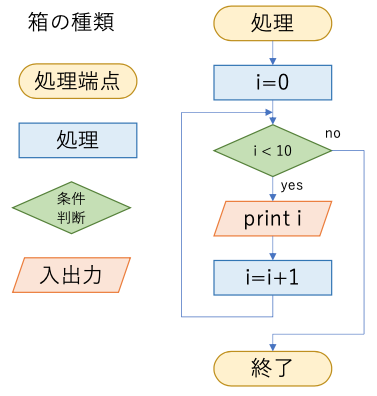 上図右側のフローチャートの例では、以下の説明のように実行され、0,1,2,…,9 が表示され、最終的に変数 i が10以上になり処理を停止する。
上図右側のフローチャートの例では、以下の説明のように実行され、0,1,2,…,9 が表示され、最終的に変数 i が10以上になり処理を停止する。
(1) 変数 i に 0 を保存
(2) 変数 i は10未満なら(3)、10以上なら終了
(3) 変数 i を表示
(4) i = i + 1 右辺の計算結果を、左辺に代入。iが0から1に変化
(5) 処理(2)から繰り返し。
上記のようなプログラムは、C言語であれば以下のようになる。
#include <stdio.h> | 入出力関数を使うための準備
int main() { | 最初に main() という関数が呼び出される。
int i ; | 変数 i の入れ物を準備
for( i = 0 ; i < 10 ; i++ ) { | 最初に i = 0 を行い、i < 10 の条件を満たす間繰り返し、
| 繰り返しの度に i を1つ増やす
printf( "%d\n" , i ) ; | i の値を表示
}
return 0 ; | 正しく終わったら0を返す。
}
練習問題1
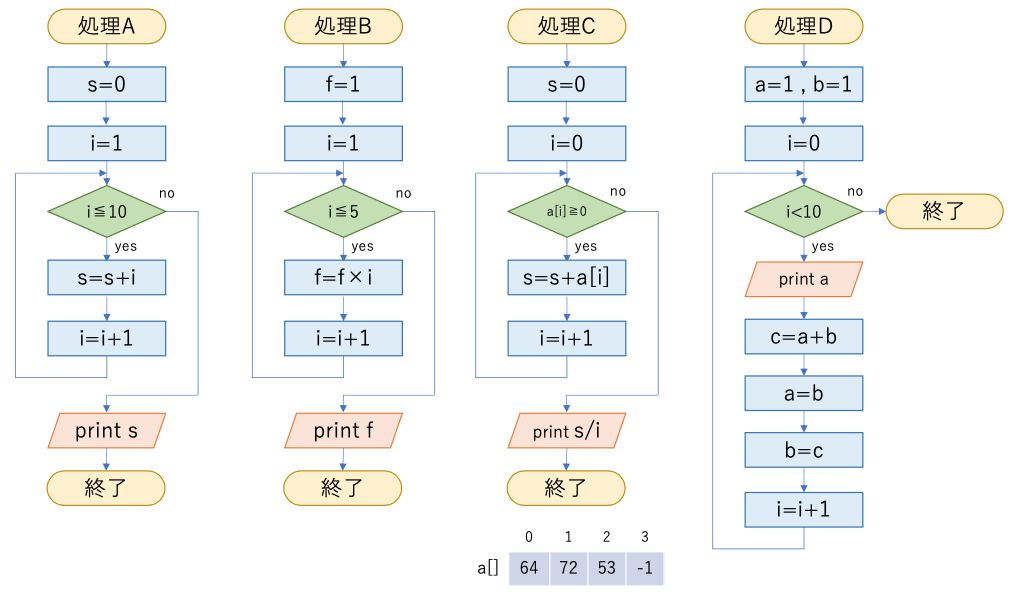
以下のフローチャートの処理A,処理B,処理C,処理Dの実行結果を答えよ。
- 電気電子工学科,電子情報工学科の学生は、出席番号が偶数は処理C,奇数は処理Dについて回答せよ。
- それ以外の学科の学生は、出席番号が偶数は処理A,奇数は処理Bの結果について回答せよ。
- このプログラムではどういった意味の値を求めようとしているのか答えよ。
情報量の単位
データを覚える最小単位は、0と1の2通りで表される1bit (ビット)と呼ぶ。単位として書く場合には b で表す。さらに、その1bitを8個組み合わせると、256通りの情報を保存できる。256通りあれば一般的な英数字などの記号を1文字保存する入れ物として便利であり、この単位を 1byte (バイト) と呼ぶ。単位として書く場合には B で表す。
通信関係の人は8bit=1byteを1オクテットと呼ぶことも多い。日本語を表現するには、かなや漢字を使うため16bit = 2byte = 1word(ワード) で表現することが多い。(ただしワードは32bitを意味することもあるので要注意, double word=32bit, quad word=64bit という呼び方もある。)
物理では単位が大きくなると、103=kキロ,106=Mメガ,109=Gギガ,1012=Tテラ を使うが、コンピュータの世界では、103≒210=1024 なので、1kB(キロバイト)というと1024Bを意味することが多い。明確に区別する時は、1024B(バイト)=1KiB(キビバイト), 10242B=1MiB(メビバイト), 10243B=1GiB(ギビバイト) などと記載する。
2進数,8進数,16進数
プログラムの中で整数値を覚える場合は、2進数の複数桁で記憶する。例えば、2進数3桁(3bit)であれば、000, 001, 010, 011, 100, 101, 110, 111 で、10進数であれば 0~7 の8通りの値が扱える。(8進数)
2進数4桁(4bit)であれば、0000, 0001, 0010, 0011, 0100, 0101, 0110, 0111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111 の16通りを表現できる(16進数)。これを1桁で表現するために、0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F を使って表現する。
例 8進数 16進数
0123 0x123 ※C言語では、
+ 026 + 0xEA 8進数を表す場合、先頭に0をつけて表す。
-------- -------- 16進数を表す場合、先頭に0xをつけて表す。
0151 0x20D 0x3+0xA = 0xD
0x2+0xE = 2+14 = 16 = 0x0 + 桁上がり
0x1+桁上がり = 0x2
整数型と扱える値の範囲
コンピュータの開発が進むにつれ計算の単位となるデータ幅は、8bit, 16bit, 32bit, 64bit と増えていった。整数型データには、正の値しか覚えられない符号無し整数と、2の補数で負の数を覚える符号付き整数に分けられる。
プログラムを作るためのC言語では、それぞれ 8bitの文字型(char)、16bitの short int型、32bitの int 型、64bitの long int 型(※C言語では long int で宣言すると32bitの環境も多いので要注意)があり、それぞれに符号なし整数(unsigned), 符号あり整数(signed: C言語の宣言では書かない)がある。
| 精度 | 符号あり | 符号なし |
| 8bit(1byte) | char (int8_t) | unsigned char (uint8_t) |
| 16bit(2byte) | short int (int16_t) | unsigned short int (uint16_t) |
| 32bit(4byte) | int (int32_t) | unsigned int (uint32_t) |
| 64bit(8byte) | long int※ (int64_t) | unsigned long int※ (uint64_t) |
符号付きのデータは、負の数は2の補数によって保存され、2進数の最上位bit(符号ビット)は負の数であれば1、正の数であれば0となる。
整数型で扱える数
(例) 符号なしの1byte(8bit)であれば、いくつの数を扱えるであろうか?
符号なしの N bit の整数であれば2N通りの値を表現でき、0~(2N-1) までの値が扱える。
| bit数 | 型 | 符号なし(unsigned) | |
| 8 | unsigned char | 0~28-1 | 0~255 |
| 16 | unsigned short int | 0~216-1 | 0~65535 |
| 32 | unsigned int | 0~232-1 | 0~4294967295 |
符号付きの N bit の整数であれば、2の補数表現では最上位ビット(MSB)が符号を表すために使う。8bitの符号付整数-100を考えると:
| 10進数 | 16進数 | 2進数 | |
| 100)10 | 64)16 | 0110,0100)2 | |
| -100)10 | 9C)16 | 1001,1100)2 | |
正の数なら残りの(N-1)bitで扱うため 0〜2N-1-1を表現できる。負の数は2N-1通りを表現できるので、N bit の符号つき整数は、-2N-1 〜0〜 2N-1-1の範囲の値を覚えられる。
| bit数 | 型 | 符号あり(signed) | |
| 8 | char | -27~0~27-1 | -128~127 |
| 16 | short int | -215~0~215-1 | -32768~32767 |
| 32 | int | -231~0~231-1 | -2147483648~2147483647 |
2の べき乗 の概算
プログラムを作る場合、2のべき乗がだいたいどの位の値なのか知りたいことが多い。この場合の計算方法として、2つの方法を紹介する。
- 232 = 22 × (210)3 = 4 × 10243 ≒ 4,000,000,000
- 232をN桁10進数で表すとすれば
なので、両辺のlog10を求める。
(つまり、bit数に0.3をかければ10進数の桁数が求まる。)
数値の範囲の問題で動かないプログラム
この話だけだと、扱える数値の上限について実感がわかないかもしれないので、以下のプログラムをみてみよう。(C言語の詳細は説明していないので、問題点がイメージできるだけでいい。)
組み込み系のコンピュータでは、int 型で宣言される変数でも、16bitの場合もある。以下のプログラムは期待した値が計算できない例である。以下の例では、16bit int型として short int で示す。
// ✳️コード1
#include <stdio.h>
#include <math.h>
int main() { // 原点から座標(x,y)までの距離を求める
short int x = 200 ;
short int y = 200 ;
short int r2 = x*x + y*y ; // (x,y)までの距離の2乗
short int r = sqrt( r2 ) ; // sqrt() 平方根
printf( "%d\n" , r ) ; // 何が求まるか?
return 0 ; // (例) 200√2 = 282ではなく、120が表示された。
}
コンピュータで一定時間かかる処理を考えてみる。
// コード2.1 // 1 [msec] かかる処理が以下のように書いてあったとする。 short int i ; for( i = 0 ; i < 1000 ; i++ ) NOP() ; // NOP() = 約1μsecかかる処理とする。 // ✳️コード2.2 // 0.5 [sec]かかる処理を以下のようにかいた。 short int i ; for( i = 0 ; i < 500000 ; i++ ) NOP() ; // でもこの処理は16bitコンピュータでは、1μsecもかからずに終了する。なぜか?
上記の例は、性能の低い16bit コンピュータの問題で、最近は32bit 整数型のコンピュータが普通だし、特に問題ないと思うかもしれない。でも、32bit でも扱える数の範囲で動かなくなるプログラムを示す。
OS(unix) では、1970年1月1日からの経過秒数で時間(unix時間)を扱う。ここで、以下のプログラムは、正しい値が計算できなかった有名な例である。(2004年1月11日にATMが動かなくなるトラブルの原因だった)
// ✳️コード3.1 int t1 = 1554735600 ; // 2019年4月09日,00:00 int t2 = 1555340400 ; // 2019年4月16日,00:00 // この2日の真ん中の日を求める。 // t1 | t2 // |--------+--------| // | t_mid | // 以下のプログラムは、正しい 2019年4月12日12:00 が求まらない。なぜか? int t_mid = (t1 + t2) / 2; // (例) 1951年03月25日 08:45 になった。 // コード3.2 // 以下のプログラムは正しく動く。 time_t 型(時間処理用の64bit整数)を使えば問題ない。 time_t t1 = 1554735600 ; // 2019年4月09日,00:00 time_t t2 = 1555340400 ; // 2019年4月16日,00:00 // time_t型が32bitであったとしても桁溢れない式 time_t t_mid = t1 + (t2 - t1) / 2 ;
練習問題2
以下の整数の範囲を具体的な値で答えよ。
出席番号・自分の誕生日(の日にち)に合わせて該当する2問について答えること。
- 7bitの符号なし整数で扱える数値の範囲 (出席番号が偶数)
- 12bitの符号あり整数で扱える数値の範囲 (出席番号が奇数)
- 20bitの符号なし整数で扱える数値の範囲 (誕生日の日づけが偶数)
- 24bitの符号あり整数で扱える数値の範囲 (誕生日の日づけが奇数)
練習問題3
先に示した数値の範囲が原因で動かないプログラム(コード1,コード2.2,コード3.1)の中から1つを選んで、計算結果が正しく求まらない原因を、具体的な値を示しながら説明せよ。
練習問題1,練習問題2,練習問題3について、レポートとして提出せよ。
Teamsのこちらの共有フォルダに、回答記入用のひな型がおいてあるので、この書式を参考に各自レポートにまとめ、同フォルダに提出してください。
コンピュータとN進数
3年の情報制御基礎の授業の一回目。この授業では、情報系以外の学生も受講することから、基礎的な共通的な話題を中心に説明を行う。
情報制御基礎のシラバス
情報制御基礎では、ここに上げたシラバス(2025)に沿って授業を行う。
基本的に、センサーから読み取ったデータを使って動く制御系システムを作る場合の基礎知識ということで、アナログ量・デジタル量の話から、移動平均やデータ差分といった数値処理や、そこで求まった値を制御に用いるための基礎的な話を行う。
コンピュータと組み込み系
最近では、コンピュータといっても様々な所で使われている。
- 科学技術計算用の大型コンピュータ(最近なら富岳や京が有名)や
- インターネットの処理を行うサーバ群
(必要に応じてサービスとして提供されるものはクラウドコンピューティングと呼ぶ)、 - デスクトップパソコン・ノートパソコン
- タブレットPCやスマートフォンのような端末、
- 電化製品の中に収まるようなワンチップコンピュータ
などがある。(3)のパソコンでもグラフィックス表示機能のために GPU(Graphics Processing Unit) を搭載したものは(ゲームでの3次元表示用)、高速計算に使われることも多い。最近では、GPU をAIの処理における神経細胞を真似するニューラルネットワークの計算に使うことも増えてきて、GPU を NPU(Neural Processing Unit)と呼ぶこともある。

(5) ワンチップコンピュータ:PIC 12F675
身近で使われている情報制御という点では、(5)のような小型のコンピュータも多く、こういったものは組み込み型コンピュータとも呼ばれる。しかし、こういったコンピュータは、小さく機能も限られているので、
- 組み込み系では、扱える数値が整数で 8bit や 16bit といった精度しかなかったり、
- 実数を伴う複雑な計算をするには、処理時間がかかったりする
ため、注意が必要である。
この情報制御基礎の授業では、組み込み系のコンピュータでも数値を正しく扱うための知識や、こういった小さいコンピュータで制御を行うことを踏まえたプログラミングの基礎となる知識を中心に説明を行う。
2進数と10進数
コンピュータの中では、電圧が高い/低いといった状態で0と1の2通りの状態を表し、その 0/1 を組み合わせて、大きな数字を表す(2進数)。
練習として、2進数を10進数で表したり、10進数を2進数に直してみよう。
N進数を10進数に変換
N進数で “abcde” があったとする。(2進数で”10101)2“とか、10進数で”12345)10“とか)
この値は、以下のような式で表せる。
(例1)
(例2)
10進数をN進数に変換
N進数のは、前式を変形すると、以下のような式で表せることから、
値をNで割った余りを求めると、N進数の最下位桁eを取り出せる。
このため、10進数で与えられた35を2進数に変換するのであれば、35を2で次々と割った余りを、下の桁から書きならべれば2進数100011)2が得られる。
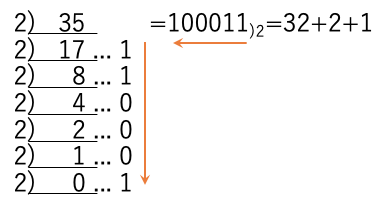
実数の場合
途中に小数点を含むN進数のab.cde)Nであれば、以下の値を意味する。
ここで、小数点以下だけを取り出した、0.cde)Nを考えると、
の値に、Nをかけると、次のように変形できる。
この式を見ると、小数部にNをかけると、整数部分に小数点以下1桁目が取り出せる。
このため、10進数で与えられた、0.625を2進数に変換するのであれば、0.625に次々と2をかけて、その整数部を上の桁から書きならべれば、2進数0.101)2が得られる。
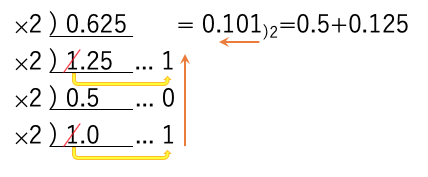
ただし、10進数で0.1という値で、上記の計算を行うと、延々と繰り返しが発生する。つまり、無限小数になるので注意せよ。
2の補数と負の数
コンピュータの中で引き算を行う場合には、2の補数がよく使われる。2の補数とは、2進数の0と1を入替えた結果(1の補数)に、1を加えた数である。

元の数に2の補数
を加えると(2進数が8bitの数であれば)、どのような数でも1,0000,0000という値になる。この先頭の9bit目が必ずはみ出し、この値を覚えないのであれば、元の数+2の補数=0とみなすことができる。このことから、2の補数= (-元の数) であり、負の数を扱うのに都合が良い。
練習問題
(1) 自分の誕生日で、整数部を誕生日の日、小数点以下を誕生日の月とした値について、2進数に変換せよ。(例えば、2月7日の場合は、”7.02″という小数点を含む10進数とする。)
変換の際には、上の説明の中にあるような計算手順を示すこと。また、その2進数を10進数に直し、元の値と同じか確認すること。(ただし、結果の2進数が無限小数になる場合最大7桁まで求めれば良い。同じ値か確認する際には無限少数の場合は近い値になるか確認すること)
(2) 自分の誕生日の日と、自分の学籍番号の下2桁の値を加えた値について、8bitの2進数で表わせ。(2月7日生まれの出席番号13番なら7+13=21)
その後、8bitの2進数として、2の補数を求めよ。また、元の数と2の補数を加えた値についても検証すること。
レポートの提出先は、こちらのリンクを参照(この中にレポート書式のひな型を置いてあります)
差分とフィードバック制御
情報制御基礎の授業を通して、入力値を制御するため、コンピュータを使う場合の数値処理の基礎的な話として、信号の平滑化を説明してきたので、最後に差分について説明をする。また、実際には、入力値を制御に利用する一般的な構成のフィードバック制御について説明する。
変化の検出
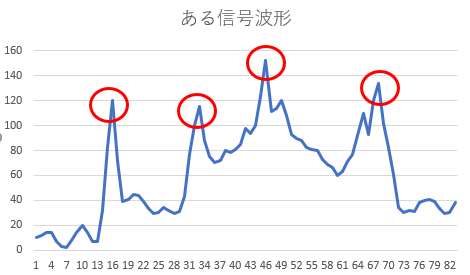
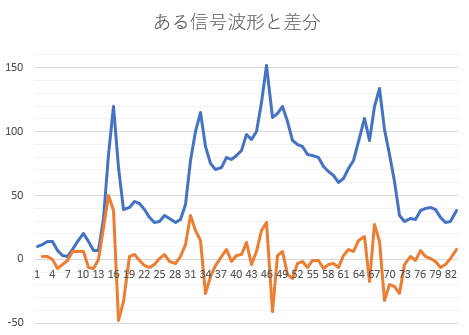
例えば、以下のような若干のノイズが混ざった入力信号が与えられたとする。この波形で「大きな山が何ヶ所ありますか?」と聞かれたら、いくつと答えるべきであろうか?山の判断方法は色々あるが、4カ所という答えは、1つの見方であろう。では、この4カ所という判断はどうすればいいだろうか?
こういった山の数を数えるのであれば、一定値より高いか低いか…という判断方法もあるだろう。この絵であれば、15ステップ目、32ステップ目付近は、100を越えていることで、2つの山と判断できるだろう。
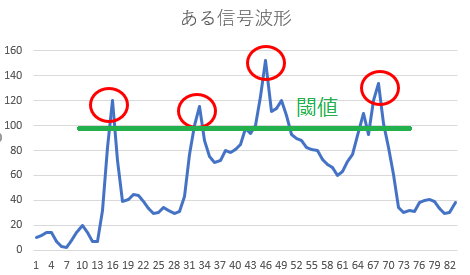
こういった予め決めておいた値より「上か?/下か?」で判断するときの基準値は、しきい値(閾値:threshold)と呼ぶ。
しかし、この閾値では、40ステップ目から50ステップ目も100を越えており、以下のようなプログラムを書いたら、40ステップ目~50ステップ目すべてをカウントしてしまう。
#define THRESHOLD 100
int x[ 100 ] = {
// 波形のデータが入っているとする。
} ;
int count = 0 ;
for( int i = 0 ; i < 100 ; i++ ) {
if ( x[i] >= THRESHOLD )
count++ ;
}
また、65ステップ目の小さな山も1個とカウントしてしまう。
この問題を避けるために、閾値を130にすると、今度は最初の2つの山をカウントできない。どうすれば、山の数をうまくカウントできるのだろうか?
差分を求める
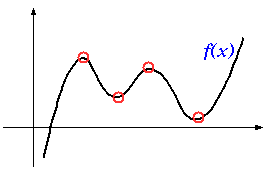
前述のような問題で山の数を数える方法を考えていたが、数学で山を見つける時には、何をするだろうか?
数学なら、山や谷の頂点を求めるのならば、微分して変化量が0となる場所を求めることで、極大値・極小値を求めるだろう。そこで、山を見つけるために入力値の変化量を求めてみよう。
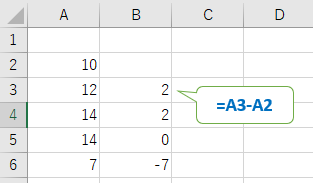
表計算ソフトで差分を計算するのであれば、セルに図のような式を入力すればいいであろう。このようなデータ点で前の値との差を差分と呼ぶ。数学であれば、微分に相当する。
このグラフを見ると、波形が大きく増加する部分で、差分が大きな正の値となる。さらに波形が大きく減少する部分で差分が負の大きな値となる。特にこのデータの場合、山と判断したい部分は差分が20以上の値の部分と定義することも考えられる。
#define TH_DIFF 20
int x[ 100 ] = {
// 波形のデータが入っているとする。
} ;
int count = 0 ;
for( int i = 0 ; i < 100 ; i++ ) {
if ( x[i] - x[i-1] >= TH_DIFF
&& x[i+1] - x[i] <= -TH_DIFF )
count++ ;
}
しかし、このプログラムでは、山の数をうまくカウントしてくれない。うまく、山の数を数えるためには、差分の値を山と判断するための閾値(この場合は20)を調整することになるだろう。
移動平均との差
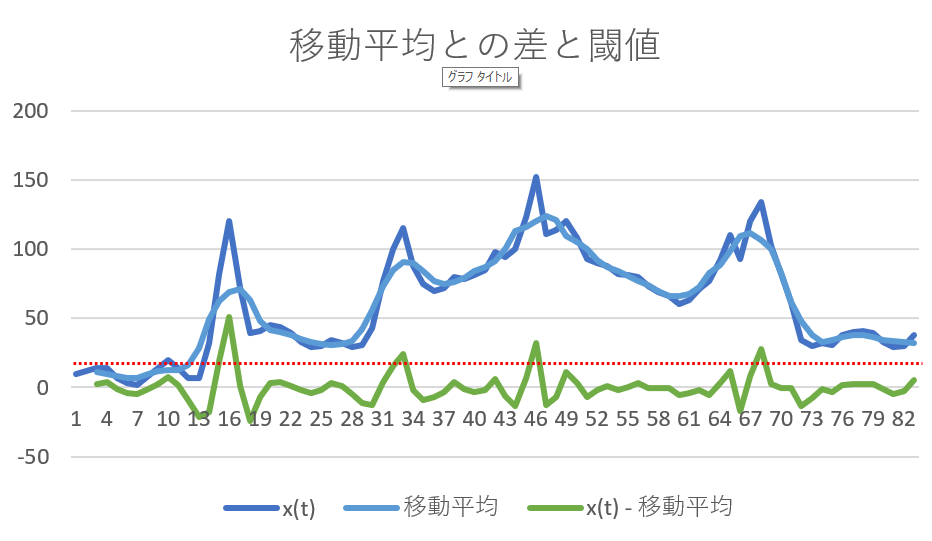
前回の講義で示したデータの例で、移動平均を取ると分かる事例ということで、船につけられた加速度センサーで、長い周期の波による船の揺れと、短い周期のエンジンによる振動があったとき、エンジンの振動を移動平均で取り除くことができるという事例を示した。
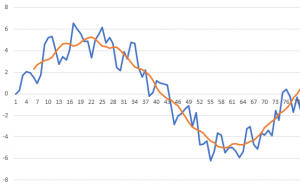
これを逆手にとれば、元の信号と移動平均の差を取れば、エンジンの振動だけを取り出すことも可能となる。以下は、前の事例で、前後5stepの移動平均(水色線)と元信号(青線)の差をとったものが緑線となっている。このような方法をとれば、元信号の短い周期の変動を抽出することができる。
制御工学の概要
以下に、制御工学ではどのようなことを行うのか、概要を述べる。
ここで紹介する制御理論は、古典制御理論と呼ばれる。
制御工学では、入力値と、何らかの処理を施し出力値
が得られるシステムで、どのように制御するかを考える。
例えば、電気ポットの温度制御をする場合、設定温度の値を入力値とし、何らかの処理を行い、出力となるヒーターの電流を制御し、最終的には温度
が測定される。ヒーターは、設定温度
と温度計の値
の差
に応じて電流量を変化させる。このように一般的な制御では、最終的な温度が入力に戻っている。このように目標値に近づけるために、目標値との差に応じて制御することをフィードバック制御という。
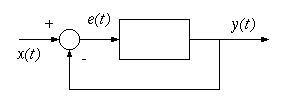
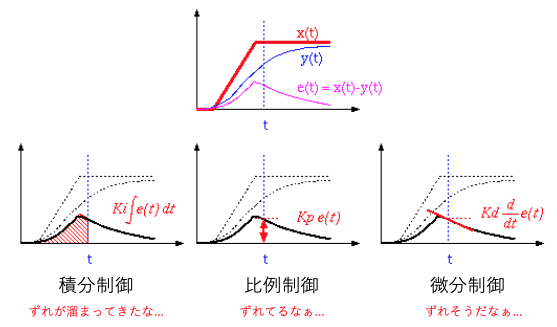
制御の仕方には様々な方法があるが、 がとある時間で0からYに変化した場合を考える。入力と出力で制御された波形の例を示す。
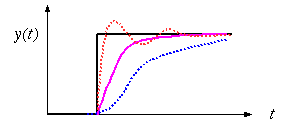
この波形では、黒のように入力値が変化した場合、それに追いつこうと出力が変化する。(1)理想的には、速やかに追いつく赤のように変化したい。しかし、(2)慎重に制御をする人なら、変化への制動が大きい過制動(青点線)となり、目標値に追いつくまでに時間がかかる。(3)一方、すこしでもずれたら直そうとする人なら、時間的には速い反応ができるかもしれないが、目標値を追い越したり、増えすぎ分を減らしすぎたりして脈動する過制御(赤点線)となるかもしれない。
PID制御
目標値、出力
、ずれ(偏差)
、制御量
とした時、基本的なフィードバック制御として偏差の使い方によってP動作,I動作,D動作がある。参考 Wikipedia PID制御
比例制御(P制御)
偏差に比例した制御を行う方式(を比例ゲインと呼ぶ)
今年のコロナ騒動を例にとるならば、比例制御は、今日の感染者数y(t)と目標としたい感染者数x(t)の差に応じて、対策の強さu(t)を決めるようなもの。
積分制御(I制御)
偏差のある状態が長い時間続く場合、入力値の変化を大きくすることで目標値に近づけるための制御。(は積分ゲイン)
積分制御は、目標の感染者数x(t)を感染者数y(t)が超えた累積患者数に応じて、対策を決めるようなもの。
移動平均は、一定範囲の値の和(を範囲のデータ数で割ったもの)であり、積分制御は移動平均の値に応じて制御するとみなすこともできる。
微分制御(D制御)
急激な出力値の変化が起こった場合、その変化の大きさに応じて妨げようとする制御。(は微分ゲイン)
微分制御は、目標数と感染者数の差が、前日よりどのぐらい増えたか(患者の増減の量:変化量)に応じて、対策を決めるようなもの。
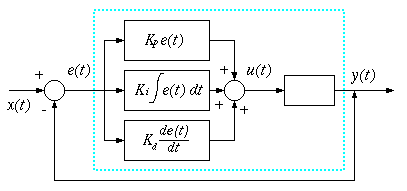
PID制御
上記のI制御やD制御だけでは、安定させることが難しいので、これらを組み合わせたPID制御を行う。
この中で、の値は、制御が最も安定するように調整を行うものであり、数値シミュレーションや、ステップ応答を与えた時の時間的変化を測定して調整を行う。
移動平均の処理
前回の授業で説明したようなA/D変換した数値データを読み取った場合、どのようなことが発生するか考える。
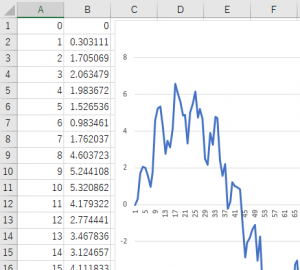
例えば、以下に示すような測定値があったとする。
このデータの一部をグラフ化してみると、次のような波形であった。
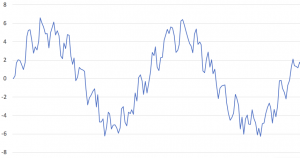
この波形をみると、大きく見ればsinカーブだが、細かい点を見るとデータにブレがある。
誤差の原因
このような測定結果が得られた場合、本来コンピュータで処理したいデータは何であろうか?
原因は様々なものが考えられるが、
- 回路のノイズ対策が不十分で、外部の電気的な影響が混入。
オシロスコープで周期を図ると、60Hz なら、交流電源だったり… - D/A 変換を行う場合には、量子化誤差かもしれない。
例えば、最初の波形が、加速度センサーの値であったとして、船の上で揺れているために、大きな周期で加速度が変化しているかもしれない。一方で、船自体がエンジンによる揺れで加速度が変化しているかもしれない。
船の中で波の揺れと、エンジンの揺れが観測されている加速度センサーの情報で、船の揺れの大きさ・揺れの周期を知りたい場合、どうすればいいだろうか?
移動平均を計算してみる
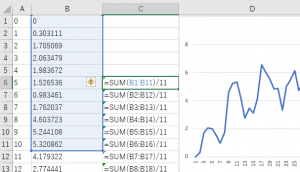
このデータを見ると、10個のデータまでの間で、波形が上下に変動している。船の揺れとエンジンの揺れが原因であれば、10個ぐらいのデータのゆらぎが、エンジンによる揺れと考えられる。では、この10個ぐらいの範囲で値が上下の影響を減らしたければ、どうすればいいか?一番簡単な方法は、前後10個のデータで平均を取ればいいだろう。増減する値を加えれば、プラスの部分とマイナスの部分の値が相殺されて0に近くはず。そこでは、Excel で前後データの平均をとってみよう。
Excelで前後11点の平均を求める式をセルに入れる
青線:元波形データ(B列)、赤線:前後11点の平均(C列)
このように、データの前後の決められた範囲の平均を平均する処理は、移動平均(単純移動平均)と呼ぶ。
時間tにおけるデータをとした場合、前後5点の移動平均
は、以下のような式で表せるだろう。
単純移動平均
単純移動平均は、時刻tの平均を、その前後のデータで平均を求めた。この方式は、実際には与えられた波形のデータを全部記録した後に、単純移動平均をとる場合に有効である。
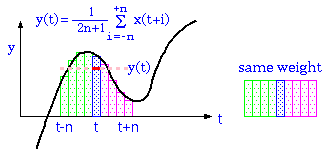
しかし、時々刻々変化する測定値の平均をその都度使うことを考えると、上記の方法は、未来の測定値
を使っていることから、現実的ではない。
// 単純移動平均(未来の値も使う)
#define NS 3
int x[ SIZE ] ; // 入力値
int y[ SIZE ] ; // 出力値
for( int t = NS ; t < SIZE-NS ; t++ ) {
int s = 0 ;
for( int i = -NS ; i <= +NS ; i++ ) // 2*NS+1回の繰り返し
s += x[t+i] ;
y[t] = s / (2*NS + 1) ;
}
過去の値だけを使った移動平均
そこで、過去の値だけで移動平均をとることも考えられる。
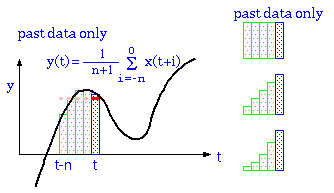
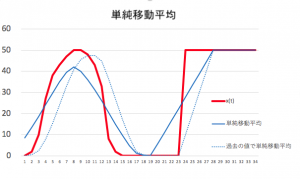
この、単純移動平均と、過去の値だけを使う単純移動平均を、適当な測定値に対して適用した場合のグラフの変化を Excel によってシミュレーションした結果を以下に示す。
しかし、このグラフを見ると、波形後半の部分に注目するとよく分かるが、過去の値だけを使った移動平均では、測定値が立ち上がったのを追いかけて値が増えていく。これでは移動平均は時間的な遅れとなってしまう。
// 未来の値を使わない単純移動平均
for( int t = NS ; t < SIZE ; t++ ) {
int s = 0 ;
for( int i = 0 ; i <= NS ; i++ ) // NS+1回の繰り返し
s += x[t-i] ;
y[t] = s / (NS+1) ;
}こ
コロナ感染者数のデータの見せ方
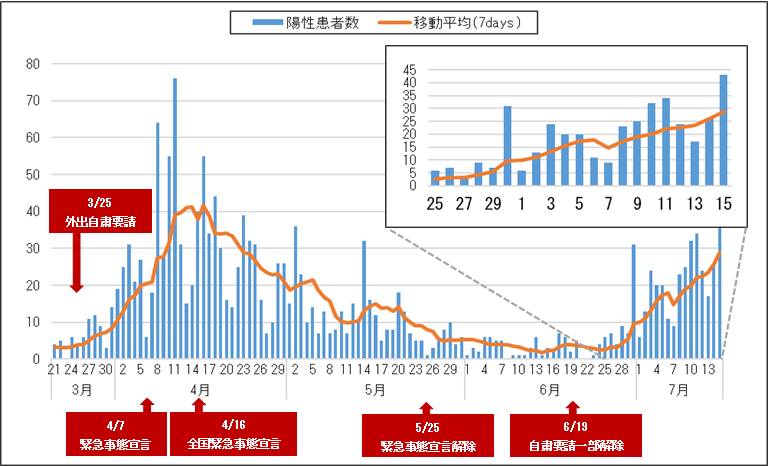
昨年までは、コロナ感染者数の増減のグラフを見る機会が多かった。例えば、以下のようなグラフ(神奈川県のデータを引用)を見ると、新規感染者数は青の棒グラフで示されている。しかし、土日の検査が月曜に計上されたりするため、青の棒グラフは週ごとに増減があって分かりにくいため、移動平均の値が合わせてオレンジ色の折れ線グラフで表示されている。しかし、オレンジ色のグラフは、青のグラフより少し右にずれていると思いませんか?
これは、移動平均といっても過去7日間の平均をグラフ化しているため、数日分だけ右にずれているように見えている。ずれが無いように見せたいのなら、3日前から3日後のデータの移動平均であれば、ずれは無くなると思われる。
加重移動平均
過去の値を使った移動平均では遅れが発生する。でも、平均を取る際に、「n回前の値」と「現在の値」を考えた時、「その瞬間の平均値」は「現在の値」の方が近い値のはず。であれば、平均を取る時に、「n回前の値は少なめ」「現在の値は多め」に比重をかけて加算する方法がある。
for( int t = 3 ; t < SIZE ; t++ ) {
// 数個の移動平均だし、
// ループを使わずに書いてみる。
int s = x[t] * 3 // 現在の値は大きい重み
+ x[t-1] * 2 // 1つ前の値
+ x[t-2] * 1 ; // 2つ前の値(重みは最小)
y[t] = s / (3+2+1) ;
}
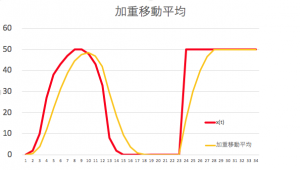
この様に、過去に遡るにつれ、平均をとる比重を直線的に小さくしながら移動平均をとる方法は、加重移動平均と呼ばれる。以下にその変化をExcelでシミュレーションしたものを示す。
指数移動平均
ここまで説明してきた、単純移動平均や、加重移動平均は、平均をとる範囲の「過去の値」を記憶しておく必要がある。広い時間にわたる移動平均をとる場合は、それに応じてメモリも必要となる。これは、組み込み型の小型コンピュータであれば、メモリが足りず平均処理ができない場合もでてくる。
そこで、荷重移動平均の重みを、は、100%,
は50%,
は25%… というように、過去に遡るにつれ、半分にして平均をとる。
しかし、以降の項で、
を使うと以下のように書き換えることができる。
// 指数移動平均は、プログラムがシンプル
// 1つ前の平均y[t-1]を覚えるだけでいい。
for( int t = 1 ; t < SIZE ; t++ ) {
y[t] = ( x[t] + y[t-1] ) / 2 ;
}
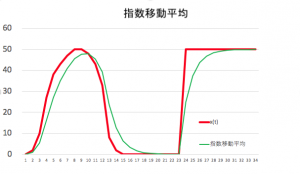
この方法であれば、直前の平均値を記録しておくだけで良い。このような移動平均を、指数移動平均と呼ぶ。
ここで示した指数移動平均は、過去を遡るにつれとなっているが、これをさらに一般化した指数移動平均は、以下の式で示される。前述の移動平均は、
とみなすことができる。
#define ALPHA 0.5
for( int t = 1 ; t < SIZE ; t++ ) {
y[t] = ALPHA * x[t] + (1.0 - ALPHA) * y[t-1] ;
}
以下のプログラムは、うまく動かない。理由を説明せよ。
#define RVA 4 for( int t = 1 ; t < SIZE ; t++ ) { // 以下はy[t]は全部ゼロになる。 y[t] = 1/RVA * x[t] + (1.0 - 1/RVA) * y[t-1] ; // 以下は、整数型演算だけで、正しく動くだろう。 // y[t] = ( x[t] + (RVA-1) * y[t-1] ) / RVA ; }
理解度確認のための小レポート
上記の移動平均の理解のために、以下の資料(講義では印刷資料を配布)の表の中を、電卓などを使って計算せよ。
計算したら、その結果をグラフの中にプロットし、どういった波形となるか確認し、レポートとして提出すること。
この課題は、こちらの Teams フォルダに提出してください。
D/A・A/D変換回路と誤差
小型コンピュータを使った制御では、外部回路に指定した電圧を出力(D/A変換)したり、外部の電圧を入力(A/D変換)したりすることが多い。以下にその為の回路と動作について説明する。
D/A変換回路
ラダー抵抗回路によるD/A変換の仕組みを引用
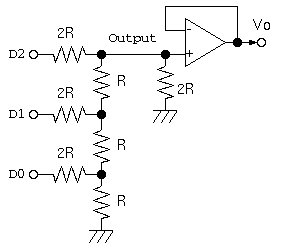
このような回路で、D0,D1,D2 は、デジタル値の0=0[V] , 1=5[V] であった場合、Output 部分の電圧は、(D0,D1,D2)の値が、(0,0,0),(0,0,1),…(1,1,1)と変化するにつれ、5/8[V]づつ増え、(1,1,1)で 5*(7/8)=4.4[V]に近づいていく。最後に、Output が出力によって電圧が変化しないように、アンプ回路を通す。
DCモータをアナログ量で制御しないこと
このように、電圧をコンピュータから制御するようになると、ロボットで模型用の直流モータの回転速度をこれで制御したい…と考えるかもしれない。
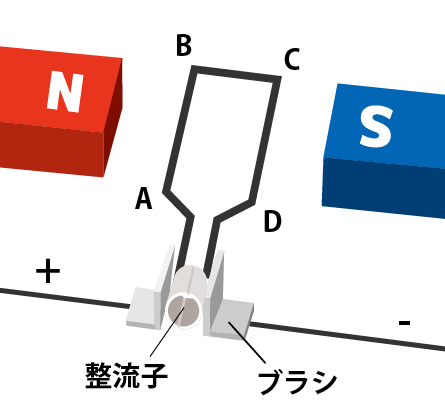
しかし、直流モータは、ブラシとコイル(電磁石)を組み合わせたものだが、モーターが回転しだす瞬間でみれば、コイルは単なる導線である。このため、小さい電流でゆっくりモータを回転させようとすると、たとえ小さい電圧でも導線(抵抗はほぼ0[Ω])には大量の電流が流れ、モータをスイッチングする回路は焼き切れるかもしれない。
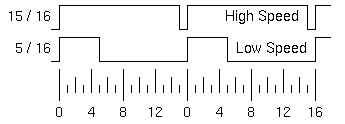
PWM変調
こういう場合には、PWM変調(Pulse Width Modulation) を行う。電圧の高さは一定で、高速回転させるときは長時間電圧をONにするが、低速回転させるときはONとOFFを繰り返し信号でONの時間を短くする。
このような波形であれば、低速度でも電流が流れる時間が短く、大量の電流消費は避けられ、モーターをまわす力も安定する。
A/D変換回路
D/A変換とは逆に、アナログ量をデジタル値に変換するには、どのようにするか?
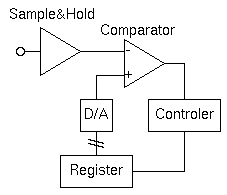
このような場合には、A/D変換回路を用いる。一般的な回路では、以下のような逐次比較型A/D変換を用いる。
この回路では、変換開始と共に入力値をサンプル保持回路でアナログ量を保存する。
その後、Registerの中のデジタル値を、D/A 変換回路でアナログ量に変換した結果を、比較器(Comparator)でどちらが大きいか判断し、その結果に応じて2分探索法とかハイアンドローの方式のように、比較を繰り返しながらデジタル値を入力値に近づけていく。
ハイアンドロー(数あてゲーム)
数あてゲームで、デタラメな0〜127までの整数を決めて、ヒントを元にその数字を当てる。回答者は、数字を伝えると、決めた数よりHighかLowのヒントをもらえる。
最も速い回答方法は…例えば決めた数が55だとすると
・初期状態 ??????? 0..127 ・64 - Low 0?????? 0..63 ・32 - High 01????? 32..63 ・48 - High 011???? 48..63 ・56 - Low 0110??? 48..55 ・52 - High 01101?? 52..55 ・54 - High 011011? 54..55 ・55 - Bingo 0110111 55確定どんな値でも、7回(27=127)までで当てることができる。
量子化と量子化誤差
アナログデータ(連続量)をデジタルデータなどの離散的な値で近似的に表すことを、量子化という。
量子化誤差とは、信号をアナログからデジタルに変換する際に生じる誤差のことをいう。
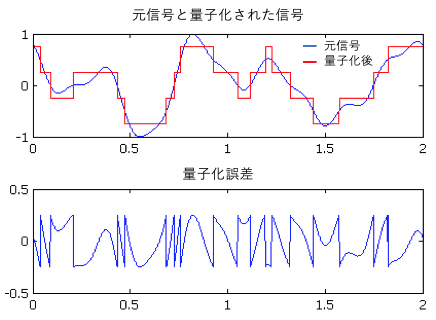
アナログ信号からデジタル信号への変換を行う際、誤差は避けられない。アナログ信号は連続的で無限の正確さを伴うが、デジタル信号の正確さは量子化の解像度やアナログ-デジタル変換回路のビット数に依存する。
偶然誤差
アナログ信号がA/D変換回路に入るまでに、アナログ部品の電気的変動(ノイズ)が原因で値が変動することもある。ノイズが時間的に不規則に発生し、値が増えてしまったり減ってしまったり偶然に発生するものは偶然誤差という。偶然誤差を加えると相殺されてほぼ0になるのであれば、統計的な手法で誤差の影響を減らすことができる。
系統誤差
ある特定の原因によって測定値が偏る誤差は、系統誤差と呼ぶ。例として、測定機器が持つ精度である器差によるもの、温度や湿度、気圧などが影響して発生するもの、測定方法の癖で値が偏るものなどがある。系統誤差は、誤差の要因が解ればその偏ったズレの量を調べて、測定した値からズレを引き算すれば補正することができる。
なぜデジタル信号を使うのか
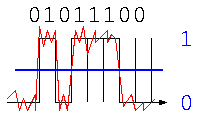
コンピュータが信号処理でなぜ使われるのか?例えば、下の信号のように、電圧の低い/高いで0/1を表現したとする。
ノイズが混入しづらい
このデータ”01011100″を通信相手に送る場合、通信の途中でノイズ(図中の赤)のような信号が加わった場合、アナログ信号では、どれがノイズなのか判別することはできない。しかしデジタル信号であれば、真ん中青線より上/下か?で判別すれば、小さいノイズの影響は無視して、元どおりの”01011100″を取り出せる。この0か1かを判別するための区切り(図中青線)は、しきい値と呼ばれる。
ノイズを見つける・治す
また、”01011100″のデータを送る通信の途中で、しきい値を越えるような大きなノイズが混ざって、受信したとする。この場合、単純に受け取るだけであれば、”01010100″で間違った値を受け取っても判別できない。しかし、データを送る際にパリティビット(偶数パリティであれば全データの1の数が偶数になるように)1ビットのデータを加える。このデータを受け取った際に、ノイズで1ビット反転した場合、1の数が奇数(3個)なので、ノイズでビット反転が発生したことがわかる。これをパリティチェックと言う。
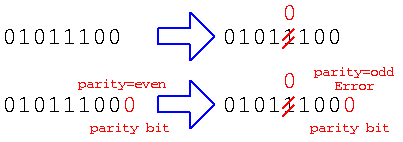
このように、デジタル信号を使えば、しきい値を越えない程度のノイズならノイズの影響を無視できるし、たとえ大きなノイズでデータに間違いがあっても、パリティチェックのような方法を使えば間違って伝わったことを判別できる。
パリティチェックは、元のデータに1bitの信号を追加することで誤り検出ができるが、2bit同時に変化してしまうと誤りを見つけられない。そこで、元データにさらに多くのbit情報を追加すると、1bitの間違いを元に戻すようにもできる。誤り検出・訂正
電子回路で制御するかコンピュータで制御するか
これ以外にも、デジタル信号にする理由がある。
アナログ回路(電子回路)で制御しようとすると、抵抗やコイルやコンデンサといった受動素子が必要となるが、その中でもコイルは小型化がしづらい部品で、制御回路全体の小型化が難しい。大量生産ができるような回路なら小型化ができるかもしれないが、多品種少量の生産物では小型化のための開発費用の元がとれない。しかし、大量生産された安価な小型コンピュータで制御すれば、制御回路全体の小型化も可能となる。
また、電子回路の特性を調整するには、抵抗などの部品をはんだ付けをしながら部品を交換することになるかもしれない。しかしながら、アナログ信号をデジタル信号にしてしまえば、ノイズを減らすための平均化処理などは計算で実現できるし、特性を変化させるための調整もプログラムの数値を変更するだけで可能となる。
表計算ソフトの使い方(絶対参照・相対参照)
今日の表計算ソフトを使った演習では、下記のサンプルファイルを練習に使うので、Teamsで参照してください。
前回課題の答え合わせ
前回のレポートでは、sin(83度)(例)といった数値の有効数字を考えるというものを考えてもらったので、この有効数字をどう記載すべきか考えてみる。
課題を示す Excel ファイルでは、75度~89度あたりの角度で出題をするようにしてあった。注意しないといけない点は、sinは90度に近づくほど、1に近づく。このため、0.99…といった数値が求まるが、角度がちょっと変化しても、0.99といった部分はほぼ変化しない。だから、83が有効数字2桁ということで、0.99 といった有効数字2桁の書き方では、ちょっと不十分かもしれない。
そこで、83度(有効数字2桁)が小数点以下を丸められた数値と仮定する。この場合、元の数値は 82.5度~83.5度 の可能性がある。これらの値のsinを計算すると、0.9914から0.9935の間であり、小数点以下3桁目は、1~3 の値であり、結果を 0.992 (有効数字3桁) と記載しても良いかもしれない。
sin(82.5°) = 0.991444861 sin(83.0°) = 0.992546152 sin(83.5°) = 0.993571856
表計算ソフトの使い方
情報制御基礎では、プログラムで計算する所を、Excel のような表計算ソフトを用いて検証してもらったりする予定なので、Excel で計算式を使う方法を説明する。
セルの場所と簡単な式
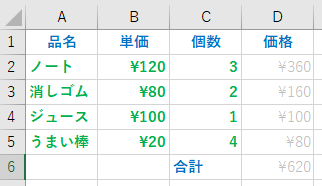
簡単な、品名・単価・個数・価格の表を考える。以下の表のように、列の名前と、品名・単価・個数まで入力した後、単価と個数をかけた価格を求めるとする。

Excel では、表の列には左から、A,B,C,D… , 表の行には上から1,2,3,4,5 と番号が振られていて、特定の列・特定の行のデータを表す時には、列行を組み合わせ、A1に品名、B3に¥80、C5に4 が入っている。
例えば、D2 に、ノート単価120円、ノート個数3個をかけた値を入れたい場合は、D2の場所に、
=B2*C2
を書き込めば、その場所には360が表示される。
先頭の”=”を入力した後、該当する”B2″の場所をクリックするなりカーソルを操作すると、カーソルのセルの場所”B2″が自動的に入力される。さらに”*”を入力した後、”C2″の場所をクリックすれば”C2″が入力される。
Excelでは、入力する文字列の先頭が”=”の場合は、残り部分は計算式として扱われる。
D3には、”=B3*C3″を入力すれば、160 が表示される。しかし、この様な式を何度も入力するのは面倒である。
この場合、セル・カーソルを、D2 に合わせ、[右ボタン]-[コピー]を行い、D3 で[右ボタン]-[貼り付けオプション]-[貼り付け]を行えば、”=B3*C3″が入力される。
ここで注意しないといけないのが、式を張り付ける場合には、貼り付け先のセルの場所が一つ下の行なので、行番号を表す2の部分が1つ下の行番号3に書き換えられて、貼り付けが行われる。(相対参照)
関数式
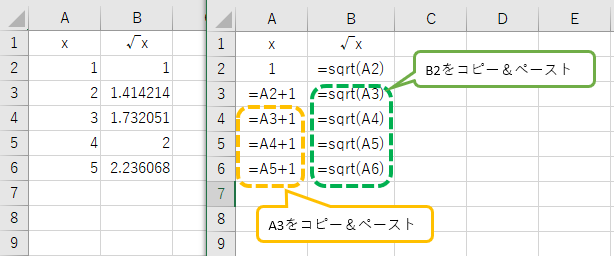
例えば、下左図のような、数字とその平方根の表を作る場合、A2 に 1、B2に =sqrt( A2 ) を入力、A3 に =A2+1 を入力したあと、B2の式をB3にコピー&ペーストし、A3,B3 を A4~A6にペーストすればいい。

B2に入力したような、sqrt( A2 ) のようなものは、関数式と呼ばれる。
また、A3,B3 といった複数の行・列をまとめた範囲を示す時は、A3:B3 といった表記方法であらわす。
絶対参照と相対参照
最初の例に戻って、単価と個数の積で今度は税率を加えて計算する例を考える。また、税率は後で変化するかもしれないので、B1 のセルに税率を記入しておく場合を考える。

この場合、D3 には、” =B3*C3*(1+B1) ” を入力すればいい。
ただ、このように式を入力すると、D3 の計算式を、D4,D5,D6 にコピーすると、セル D4 には =B4*C4*(1+B2) が入力されてしまい、B2 には単価という文字が記載されているため、正しい結果が求まらない。
こういった場合には、絶対参照を用いる。D3 に記入する式を
=B3*C3*(1+$B$2)
とし、この D3 の式を D4 にコピー&ペーストすると、列記号、行番号の前に$がついた部分の式は、貼り付け場所に応じて変化しない。
このような、$B$2 といったセルの参照は、絶対参照と呼ぶ。これに対し、B2 といったセル参照は、貼り付け場所に応じて書き換えられるので、相対参照と呼ぶ。
絶対参照と相対参照が混ざった、$B2, B$2 といった書き方もある。
式の入力時に[F4ボタン]を押す度に、B2→$B$2→B$2→$B2→B2 と変化する$B2 は、式をコピーすると列部分はBのまま、行部分は場所に合わせて変化する。
B$2 は、式をコピーすると列部分は場所に合わせて変化し、行部分は2のままとなる。
レポート課題(第5回)
Excel で、xを0〜180度まで変化させたときのsin(x),位相をyとした時のsin(x+y)の値の表を作り、グラフ機能で表示せよ。A列は角度・B列はsin(x)・C列はsin(x+y)の値とし、yの値は”C1″に保存されているものとする。
この時、計算式の入力をどのように行なったのか(相対参照や絶対参照をどのように使ったのか)説明を、グラフの下に入力欄を設け記入せよ。
なお、Excel の sin() 関数は、引数がラジアンで入力する必要があるので、計算式には注意せよ。
そして出来上がった Excel のファイルを、Teams のこちらのフォルダに提出せよ。