前回の授業で説明したハッシュ法は、データから簡単な計算(ハッシュ関数)で求まるハッシュ値をデータの記憶場所とする。しかし、異なるデータでも同じハッシュ値が求まった場合、どうすれば良いか?
ハッシュ法を簡単なイメージで説明すると、100個の椅子(ハッシュ表)が用意されていて、1クラスの学生が自分の電話番号の末尾2桁(ハッシュ関数)の場所(ハッシュ値)に座るようなもの。自分のイスに座ろうとしたら、同じハッシュ値の人が先に座っていたら、どこに座るべきだろうか?
オープンアドレス法
先の椅子取りゲームの例え話であれば、先に座っている人がいた場合、最も簡単な椅子に座る方法は、隣が空いているか確認して空いていたらそこに座ればいい。
これをプログラムにしてみると、以下のようになる。このハッシュ法は、求まったアドレスの場所にこだわらない方式でオープンアドレス法と呼ばれる。
// オープンアドレス法
// table[] は大域変数で0で初期化されているものとする。
// 配列に電話番号と名前を保存
void entry( int phone , name ) {
int idx = hash_func( phone ) ;
while( table[ idx ].phone != 0 )
idx = (idx + 1) % HASH_SIZE ; // ひとつ後ろの席
} // idx++ でないのは何故?
table[ idx ].phone = phone ;
strcpy( table[ idx ].name , name ) ;
}
// 電話番号から名前を調べる
char* search( int phone ) {
int idx = hash_func( phone ) ;
while( table[ idx ].phone != 0 ) {
if ( table[ idx ].phone == phone )
return table[ idx ].name ;
idx = (idx + 1) % HASH_SIZE ; // ひとつ後ろの席
} // idx++ でないのは何故?
return NULL ; // 見つからなかった
}
注意:このプログラムは、ハッシュ表すべてにデータが埋まった場合、無限ループとなるので、実際にはもう少し改良が必要である。
この実装方法であれば、ハッシュ表にデータが少ない場合は、ハッシュ値を計算すれば終わり。よって、処理時間のオーダはO(1)となる。しかし、ハッシュ表がほぼ埋まっている状態だと、残りわずかな空き場所を探すようなもの。
チェイン法
前に述べたオープンアドレス法は、ハッシュ衝突が発生した場合、別のハッシュ値を求めそこに格納する。配列で実装した場合であれば、ハッシュ表のサイズ以上の データ件数を保存することはできない。
チェイン法は、同じハッシュ値のデータをグループ化して保存する方法。 同じハッシュ値のデータは、リスト構造とするのが一般的。ハッシュ値を求めたら、そのリスト構造の中からひとつづつ目的のデータを探す処理となる。
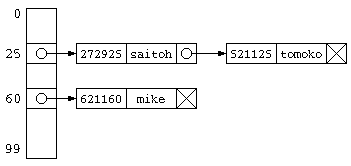
この処理にかかる時間は、データ件数が少なければ、O(1) となる。しかし、ハッシュ表のサイズよりかなり多いデータ件数が保存されているのであれば、ハッシュ表の先に平均「N/ハッシュ表サイズ」件のデータがリスト構造で並んでいることになるので、O(N) となってしまう。
#define SIZE 100
int hash_func( int ph ) {
return ph % SIZE ;
}
struct PhoneNameList {
int phone ;
char name[ 20 ] ;
struct PhoneNameList* next ;
} ;
struct PhoneNameList* hash[ SIZE ] ; // NULLで初期化
struct PhoneNameList* cons( int ph ,
char* nm ,
struct PhoneNameList* nx ) {
struct PhoneNameList* ans ;
ans = (struct PhoneNameList*)malloc(
sizeof( struct PhoneNameList ) ) ;
if ( ans != NULL ) {
ans->phone = ph ;
strcpy( ans->name , nm ) ;
ans->next = nx ;
}
return ans ;
}
void entry( int phone , char* name ) {
int idx = hash_func( phone ) ;
hash[ idx ] = cons( phone , name , hash[ idx ] ) ;
}
char* search( int phone ) {
int idx = hash_func( phone ) ;
struct PhoneNameList* p ;
for( p = hash[ idx ] ; p != NULL ; p = p->next ) {
if ( p->phone == phone )
return p->name ;
}
return NULL ;
}
文字列のハッシュ値
ここまでで説明した事例は、電話番号をキーとするものであり、余りを求めるだけといったような簡単な計算で、ハッシュ値が求められた。しかし、一般的には文字列といったような名前から、ハッシュ値が欲しいことが普通だろう。
ハッシュ値は、簡単な計算で、見た目デタラメな値が求まればいい。 (ただしく言えば、ハッシュ値の出現確率が極力一様であること)。一見規則性が解らない値として、文字であれば文字コードが考えられる。複数の文字で、これらの文字コードを加えるなどの計算をすれば、 偏りの少ない値を取り出すことができる。
int hash_func( char s[] ) {
int sum = 0 ;
for( int i = 0 ; s[i] != '¥0' ; i++ ) {
sum = sum + s[i] ;
}
return sum % SIZE ;
}
文字列順で異なる値となるように
前述のハッシュ関数は、”ABC”さんと”CBA”さんでは、同じハッシュ値が求まってしまう。文字列順で異なる値が求まるように改良してみる。
int hash_func( char s[] ) {
int sum = 0 ;
for( int i = 0 ; s[i] != '¥0' ; i++ ) {
sum = sum*2 + s[i] ;
// sum = (sum * 小さい素数 + s[i]) % 大きい素数 ;
}
return sum % SIZE ;
}
上記のプログラムの、sum = sum*2 + s[i] では、2倍していった数を最後に SIZE で割っているだけなので、文字が長い場合文字コードの値の違いが sum の中に残らない場合も考えられる。こういった場合には、以下のような方法も考えられる。大きな素数で割ることで、余りの中に、元の数の値の違いの影響が残る。これは、疑似乱数生成での剰余法(or 線形合同法)の考え方を取り入れた方法ともいえる。
#define PRIME_B 大きな素数
#define PRIME_A 小さな素数
int hash_func( char s[] ) {
int sum = 0 ;
for( int i = 0 ; s[i] != '¥0' ; i++ ) {
sum = (sum * PRIME_A + s[i]) % PRIME_B ;
}
return sum % SIZE ;
}