コロナ対策で、4年向けの情報構造論も始められないので、自習用資料。
制御構文の理解
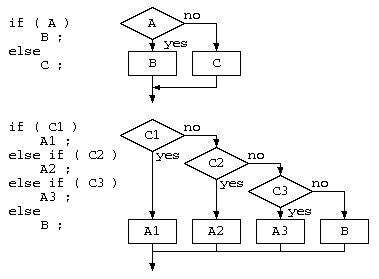
基本として、C言語の制御構文の意味をフローチャートで表すと以下のようになる。
条件分岐if
繰り返しwhile, for, do-while
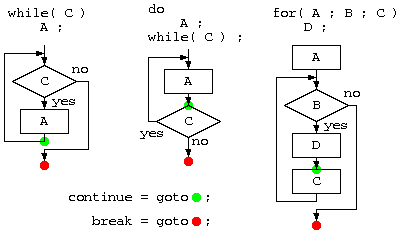 繰り返し命令の中では、break文でループを抜ける、continue文で次の繰り返し先頭に飛ぶ。フローチャートで表すと、上記の図中の赤、青の部分。
繰り返し命令の中では、break文でループを抜ける、continue文で次の繰り返し先頭に飛ぶ。フローチャートで表すと、上記の図中の赤、青の部分。
条件分岐switch
条件分岐のswitch文は、以下のようなフローチャートで示すことができる。
ただしcase の後には定数式しか書けない。 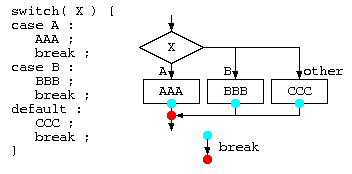 一般的には、分岐処理のAAA;BBB;CCC;の後ろには、break を書くのが一般的。繰り返し処理の中にswitch文があった場合、break命令では、switch文を抜けるだけで、ループを抜け出す訳ではない。
一般的には、分岐処理のAAA;BBB;CCC;の後ろには、break を書くのが一般的。繰り返し処理の中にswitch文があった場合、break命令では、switch文を抜けるだけで、ループを抜け出す訳ではない。
もし、breakを書き忘れると、以下のようなフローチャートになるので要注意。
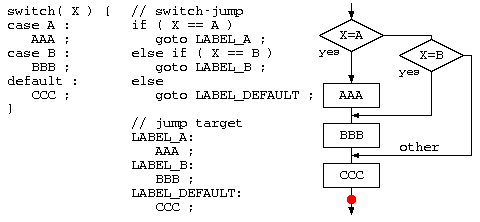 このフローチャートを見てわかるように、breakが無いと、X=Bの時、処理BBB,CCCが実行することになる。
このフローチャートを見てわかるように、breakが無いと、X=Bの時、処理BBB,CCCが実行することになる。
文の定義
C言語では、文とは(大雑把に言うと)以下の定義である。複文の所が要注意。
for()の後には1つの文が書ける。単純な計算式であれば、式;で1つの文なので、{,} は本来不要。forの中で複数の処理を書きたい時は、{ 文 文 … } のように複文で1つの文の塊をつくる。
((( C言語の文 )))
// 式 : 計算式が ; で終わっているもの
式 ;
// if文
if ( 式 ) 文
else 文 // else以下略あり
// while文
while( 式 ) 文
// for文
for( 式 ; 式 ; 式 ) 文
// do-while文
do 文 while( 式 ) ; // セミコロンまででdo-while文
// 複文
{ 文 文... } // 複数の文を1つの文として扱う
// 空文
; // for(;;); これも文法としては正しい
例題
上記の制御構文の意味を踏まえた上で、過去のテスト問題より具体例で説明。
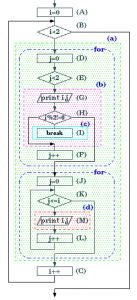
以下のプログラムの動作順序を(A)〜(M)の記号で答えよ。
答えは20ステップ目までで良い。
前述の文の定義を踏まえ、前述の問題の中では、以下の様な命令の塊(ブロック)が存在する。
ここで、水色部分(c)の if 文の break は{,} は不要なのか?という質問をする人が多いけど、if(式) { 文 } と書いても、if(式) 文 でも、文の部分に複文を使うか使わないかの違いにすぎない。
これを踏まえて、フローチャートを書くと以下の通り。
よって、この問題の回答は、以下のようになる。
| A(i=0)→ | B(i==0)→D(j=0)→ | E(j==0)→G→H→ F→ | |
| E(j==1)→G→H→I(break)→ | |||
| J(j=0)→ | K(j==0)→M→L→ | ||
| K(j==1)→ | C(i=1)→ | ||
| B(i==1)→D(j=0)→ | E(j==0)→G→H→ F→ | ||
| E(j==1)→G→H→I(break)→ | |||
| J(j=0)→ | K(j==0)→M→L→ | ||
| K(j==1)→M→L→ | |||
| K(j==2)→ | C(i=2)→ | ||
| B(i==2) |
第2回レポート課題
(1) 以下の rep1-1〜rep1-4 の中から1つを選び、処理順序の結果を答えよ。rep-1-(出席番号%4+1)を答えること。(例:出席番号10番の人はrep1-3)
rep-1-1
rep-1-2
rep-1-3
rep-1-4
(2) 以下の foo(n) , bar(n) の関数で、プログラムの(a)〜(i)の計算式の1命令の実行に10[nsec]とする。(それ以外の実行時間は無視して良い)
引数が n=2 , n=4 の場合、各関数foo(n),bar(n)の返り値 cnt の値、foo(n),bar(n) の実行にかかる時間を答えよ。ただし、答えた理由がわかるような情報をつけること。
例えば、命令に実行回数を数えるためのチェックマークの数がわかる資料でも良い。
| nの値 | foo(n) | bar(n) | ||
|---|---|---|---|---|
| cnt | 処理時間 | cnt | 処理時間 | |
| n=2 | ||||
| n=4 | ||||
(3) n=1024 の時、foo(n),bar(n)はどんな値になると思いますか?
どのように考えて計算すればいいか、考え方を提案してください。
レポート課題は、上記(1),(2),(3)を簡単に(A4×1〜2ページ)まとめ、この共有フォルダに提出して下さい。提出するファイル名は、出席番号-名前-レポート名.拡張子としてください。提出締め切りは、(2020/04/24までとする)