データベースの設計とER図
データベースの設計
リレーショナル・データベースでは、データは表形式であればなんでも良い訳ではない。
例えば、学生の成績データが以下のような構造であった場合、
ID | name | grade | subject | teacher ------+--------+-------+----------+--------- 20101 | aoyama | 1 | database | saitoh 20101 | aoyama | 1 | software | murata 20002 | suzuki | 2 | database | saitoh 20002 | suzuki | 2 | compiler | nomura 30203 | yamada | 3 | media | ogoshi
- 修正不整合: 授業担当が saitoh → sasaki のように変更になったら、複数のテーブルを修正しなければならない。大量のレコード修正は、時間がかかるし、その途中にシステムダウンしたらデータの整合性に問題が発生するかも。
- 挿入不整合: 新しい科目 internet を追加したいけど、受講学生が決まらないとデータを挿入できない。
- 削除不整合: yamada が受講を取りやめたら、科目 media も消えてしまう。
これらを考慮すると、以下のような3つの表で設計するべきである。
学生 受講 科目
ID | name | grade ID | SubID SubID | subject | teacher
------+--------+------- ------+------- ------+----------+--------
20101 | aoyama | 1 20101 | 1001 1001 | database | saitoh → sasaki
20002 | suzuki | 2 20101 | 1002 1002 | software | murata
30203 | yamada | 3 20002 | 1001 1003 | compiler | nomura
20002 | 1003 1004 | media | ogoshi
消す→ 30203 | 1004 1005 | internet | foobar → 追加
データベースの設計では、(1)概念設計、(2)論理設計、(3)物理設計が行われる。
- 概念設計:概念スキーマの決定(実体・関係モデルを使う)。上記の受講データベースの設計例
- 論理設計:論理スキーマの決定。関係データベースで実装?ほかのデータベース?
- 物理設計:物理スキーマの決定。データの格納方法や管理方法を決める。
実体関連モデル(ERモデル)
データベース設計では、実体関連モデル(ERモデル:Entity-Relation model)が使われる。 実体とは、モデル化しようとする対象で独立した存在となれるもの。 実体が持つ色々な特性は属性と呼ばれる。 属性の取りうる値の集合を定義域、同一種類の実体の集まりを実体集合と呼ぶ。 関連とは、実体同士の相互関係をモデル化したもの。
実体関連図(ER図)では、実体を長方形、関連をひし形、属性を楕円で表現する。 属性で、キーとなるものには下線をつけて表す。

ER図で調べると、実際にはもっと細かい規定で表現が行われている。 参考:IDEF1X表記とIE表記
CTF の練習問題
情報セキュリティ関係の学生の興味を引き出すために、関連のイベントに学生さんに参加してもらっている。でも、なかなか基本知識がないと参加も難しい。
こういった情報セキュリティの基本に興味を持ってもらうために、Capture The Flag という大会がある。といっても、全国の大会だとレベルが高すぎるので、まずは興味を持ってもらうための基本問題を作ったので公開しておく。
講義録に動くサンプルコードを併記
長男からプログラミングの授業の質問が LINE で流れてきて、大学の先生の資料を覗き見。その大学の課題ではサンプルコードの配布がしっかりしている。私の講義録でもサンプルコードは掲載しているけど、プロジェクタで掲示しながら授業をするため、#include 行を省略したり、main を void 宣言したりと、そのまま入れても動かない。
そこで、ダウンロードすれば「そのまま動くサンプルコード」を積極的に入れるようにしてみよう。
まずは、後期の情報構造論の半分ほどのサンプルコードを動く様に加筆し、テキストファイルへのリンクを埋め込んだ。
データベースについても、学内向けのSQLite3を使った実験環境にて動作ができるように、若干の改良を加え、リンクを埋め込んだ。
前期分は、来年度の授業の中で修正していこう。
B木とデータベース
2分探索木の考え方を拡張したもので、B木がある。
B木の構造
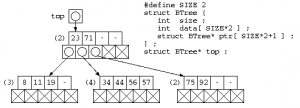
2分木では、データの増減で木の組換えの発生頻度が高い。そこで、1つのノード内に複数のデータを一定数覚える方法をとる。B木では、位数=Nに対し、最大2N個のデータd0..d2N-1と、2N+1本のポインタp0..p2Nから構成される。piの先には、di-1<x<di を満たすデータが入った B木のノードを配置する。ただし、データの充填率を下げないようにするため、データは最小でもN個、最大で2N個を保存する。
B木からデータの検索
データを探す場合は、ノード内のデータ diの中から探し、見つからない場合は、ポインタの先のデータを探す。位数がある程度大きい場合、ノード内の検索は2分探索法が使用できる。また、1つのノード内の検索が終われば、探索するデータ件数は、1/N〜1/2Nとなることから、指数的に対象件数が減っていく。よって、検索時間のオーダは、O(logN) となる。
B木へのデータの追加
B木にデータを追加する場合は、ノード内に空きがあれば、単純にデータの追加を行う。ノード内のデータが2N個を越える場合は、以下のような処理を行う。
ノード内のデータと追加データを並べ、その中央値を選ぶ。この中央値より大きいデータは、新たにつくられたノードに移す。中央値のデータは上のノードに追加処理を行う。このような方法を取ることで、2分木のような木の偏りが作られにくい構造となるようにする。
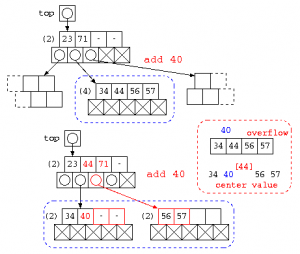
データを削除する場合も同様に、データ件数がN個を下回る場合は、隣接するノードからデータを取ってくることで、N個を下回らないようにする。
B木とデータベース
このB木の構造は、一般的にデータベースのデータを保存するために広く利用されている。
データベースシステムでは、データを効率よく保存するだけでなく、データの一貫性が保たれるように作られている。
例えば、データベースのシステムが途中でクラッシュした場合でも、データ更新履歴の情報を元にデータを元に戻し、データを再投入して復旧できなければならない。データを複数の所からアクセスした場合に、その順序から変な値にならないように、排他制御も行ってくれる。
データベースで最も使われているシステムは、データすべてを表形式で扱うリレーショナル・データベースである。
((リレーショナル・データベースの例)) STUDENT RESULT ID | name | grade | course ID | subject | point -----+----------+-------+-------- -----+---------+------- 1001 | t-saitoh | 5 | EI 1001 | math | 83 1002 | sakamoto | 4 | E 1001 | english | 65 1003 | aoyama | 4 | EI 1002 | english | 90 ((SQLの例)) select STUDENT.name, RESULT.subject, RESULT.point --射影-- from STUDENT , RESULT --結合-- where STUDENT.ID == RESULT.ID -- 串刺し -- --選択-- and RESULT.point >= 60 ; ((上記SQLをC言語で書いた場合)) for( st = 0 ; st < 3 ; st++ ) // 結合 for( re = 0 ; re < 3 ; re++ ) if ( student[ st ].ID == result[ re ].ID // 選択 && result[ re ].point >= 60 ) printf( "%s %s %d" , // 射影 student[ st ].name , result[ re ].subject , result[ re ].point ) ;
B+木
データベースの処理では、目的のデータを O(log N) で見つける以外にも、全データに対する処理も重要である。この場合、全てのデータに対する処理では、単純なB木では再帰呼び出しが必要となる。しかし、他の表でも再帰処理を伴うと、プログラムは複雑になってしまう。
そこで、B木のデータを横方向に並べて処理を行う場合に、その処理が簡単になるように B+木が用いられる。
この方法では、末端のノードは、隣接するノードへのポインタを持つ。

GROUP BY-HAVINGとCREATE VIEW
先週に引き続き、2つのSQLとそれと同じ処理のプログラム作成の課題に取り組む。
演習だけでは進度が少ないので、SQL で説明できなかった、GROUP BY-HAVING と CREATE VIEW の説明
GROUP BY HAVING
GROUP BY-HAVING では、指定されたカラムについて同じ値を持つレコードがグループ化される。SELECT 文に指定される集約関数は、グループごとに適用される。HAVING は、ある条件を満たす特定のグループを選択するための条件で、WHERE と違い、集約関数が使える。
SELECT SG.商品番号, SUM(SG.在庫量) FROM SG GROUP BY SG.商品番号 HAVING SUM(SG.在庫量) >= 500 ;
- 実験環境でGROUP-BY-HAVING(学内のみ)
このSQLを実行すると、SG のテーブルから、商品番号が同じものだけをあつめてグループ化される。そのグループごとに在庫量のデータの合計SUMを集約し、500以上のデータが出力される。
CREATE VIEW
今までで述べてきたSQLでは、実際のテーブルを対象に、結合・選択・射影を行う命令であり、これは概念スキーマと呼ばれる、対象となるデータベース全体を理解したプログラマによって扱われる。
しかし、プログラムの分業化を行い、例えば結果の表示だけを行うプログラマにしてみれば、全てのデータベースの表を考えながらプログラムを作るのは面倒である。そこで、結合・選択・射影の演算の結果で、わかりやすい単純な表となったものであれば、初心者のデータベースプログラマでも簡単に結果を扱うことができる。このような外部スキーマを構成するための機能が、ビューテーブルである。
-- 優良業者テーブルを作る --
CREATE VIEW 優良業者 ( 業者番号 , 優良度 , 所在 )
AS SELECT S.業者番号, S.優良度, S.所在
FROM S
WHERE S.優良度 >= 15 ;
-- 優良業者テーブルから情報を探す --
SELECT *
FROM 優良業者
WHERE 優良業者.所在 = '福井' ;
ビューテーブルに対する SQL を実行すると、システムによっては予め実行しておいた CREATE VIEW の AS 以下の SQL の実行結果をキャッシュしておいて処理を行うかもしれない。システムによっては SQL の命令を 副クエリを組合せた SQL に変換し、処理を行うかもしれない。しかし、応用プログラマであれば、その SQL がどのように実行されるかは意識する必要はほとんど無いであろう。
ただし、ビューテーブルに対する 挿入・更新・削除といった演算を行うと、データによっては不整合が発生することもあるので注意が必要である。
HIT2019にて優秀賞
第6回ビジネスモデル発見&発表会 北陸大会と第6回G空間×ICT北陸まちづくりトライアルコンクール、起業家甲子園・起業家万博 北陸予選を兼ねたHIT2019にて、3EIの佐野くんが優秀賞となりました。

ポインタの先には何がある?
学生さんから「ポインタの先には何があるの?」との質問があった。
私が「そのポインタの型のデータ」と答えると、さらに「ポインタはメモリの場所。でもメモリには int や char や double といった色んなデータがある。そんな色々なデータの中からデータを取り出すんだから、そこにはどんなデータが入っているのか判らないとデータを取り出せないんじゃ?」と疑問をぶつけてきた。
なるほど、本当の疑問点が見えてきた。
最近のPython等の動的型付け言語の場合
# ポインタの質問だから、C言語の場合を答えればいいんだけど…
最近の Python , PHP といった変数が型を持たない「動的型付け言語」は、まさに質問の通り。データを取り出すためには、型の情報が必要。こういう言語は、基本型以外のデータはすべて参照型(要はポインタ)なので、変数の指し示す先には型情報とそのデータがペアで保存されているので、その型情報をみてデータを取り出している。
C言語の場合(静的型付け言語)
C言語では、ポインタは単なるメモリの場所を表すだけ。ポインタの先にはデータがある。(だからデータしかないって!)
メモリからデータを読み出すときに、int 4byte で取り出すのか、 double 8byte で取り出すかどうやってわかるの?と思うかもしれないけど、そのポインタの変数がどういう型へのポインタで定義されているかプログラムを読めばわかる。それに従って取り出せばいい。こういう言語は「静的型付け言語」という。
となると「じゃあ int のデータを char として読めるの?」と思うかもしれないけど「読めるよ!」
#include <stdio.h>
int main() {
// 型を偽って参照するのは間違いの元なので型のチェックは厳格。
// だから 以下の様なヤバイことをする時は、型キャスト で
// だますことが定番。
int x = 0x41424344 ;
char* p = (char*)( &x ) ; // int型の場所をchar型にする
printf( "%c\n" , *p ) ;
// int型は4バイト、次のアドレスは?
int y[] = {
0x11223344 , 0x12345678 ,
} ;
printf( "%p %p\n" , y , y + 1 ) ;
int *r = y + 1 ;
printf( "%04d\n" , *r ) ; // 12345678 が表示
// intの1byteとなりをintとして読める?
int *q = (int*)((char*)( &y ) + 1) ;
printf( "%04x\n" , *q ) ; // 処理系によってはメモリエラー
// ポインタは番地を表す数値だよね?
// 0x100番地のデータは読める?
int* s = (int*)0x100 ;
printf( "%d\n" , *s ) ; // Segmentation Fault.
return 0 ;
}
さて、上記のプログラムをみてどう思った?
C言語って自由奔放で、やばくね? — ポインタなんか使えるからだよね、そう思うんなら Java 使え。ポインタなんか使えないから。
でも型宣言が面倒なんだよね — Python, Ruby などの動的型付けな言語使え。
でも変数参照でいちいち型情報しらべる言語って遅くね? — あるよ。「型推論」。型を明記しなくても、プログラムの文脈から型を推論してくれる静的型付け言語。Go , Swift , Kotlin…といった、今 流行りのプログラム言語がソレ。最新のJavaやC++も型推論機能が使えるようになってるよ。んで、今話題の中学生が作ったプログラム言語 Blawn も、型推論の言語!すげーな。
演算子と2分木による式の表現
2分木の応用として、式の表現を行うけどその前に…
逆ポーランド記法
一般的に 1*2 + 3*4 と記載すると、数学的には演算子の優先順位を考慮して、(1*2)+(3*4) のように乗算を先に行う。このような優先順位を表現する時に、()を使わない方法として、逆ポーランド記法がある。
演算子の書き方には、前置記法、中置記法、後置記法があり、後置記法は、「2と3を掛ける、それに1を加える」と捉えると、日本語の処理と似ている。
中置記法 1+2*3 前置記法 +,1,*,2,3 後置記法 1,2,3,*,+
後置記法は、一般的に逆ポーランド記法(Reverse Polish Notation)とも呼ばれ、式を機械語の命令に置き換える際に役立つ。
理解度確認
以下の式を指定された書き方で表現せよ。
逆ポーランド記法 1,2,*,3,4,*,+ を中置記法で表現せよ。 中置記法 (1+2)*3-4*5 を逆ポーランド記法で表現せよ。
以前の情報処理技術者試験では、スタックの概念の理解の例題として、逆ポーランド記法への変換アルゴリズムのプログラム作成が出題されることが多かったが、最近は出題されることはなくなってきた。
逆ポーランド式の実行
この逆ポーランド記法で書かれた式から結果を求めるプログラムは以下のように記述できる。このプログラムでは式を簡単にするため、数値は1桁の数字のみとする。
// 単純な配列を用いたスタック
int stack[ 10 ] ;
int sp = 0 ;
void push( int x ) {
stack[ sp++ ] = x ;
}
int pop() {
return stack[ --sp ] ;
}
// 逆ポーランド記法の計算
int rpn( char* p ) {
for( ; *p != '// 単純な配列を用いたスタック
int stack[ 10 ] ;
int sp = 0 ;
void push( int x ) {
stack[ sp++ ] = x ;
}
int pop() {
return stack[ --sp ] ;
}
// 逆ポーランド記法の計算
int rpn( char* p ) {
for( ; *p != '\0' ; p++ ) {
if ( isdigit( *p ) ) {
// ~~(A)
// 数字はスタックに積む
push( *p - '0' ) ;
} else if ( *p == '+' ) {
// 演算子+は上部2つを取出し
int r = pop() ;
int l = pop() ;
// 加算結果をスタックに積む
push( l + r ) ;
} else if ( *p == '*' ) {
// 演算子*は上部2つを取出し
int r = pop() ;
int l = pop() ;
// 乗算結果をスタックに積む
push( l * r ) ;
}//~~~~~~~~~~~~~(B)
}
// 最終結果がスタックに残る
return pop() ;
}
void main() {
printf( "%d\n" , rpn( "123*+" ) ) ;
}
' ; p++ ) {
if ( isdigit( *p ) ) {
// ~~(A)
// 数字はスタックに積む
push( *p - '0' ) ;
} else if ( *p == '+' ) {
// 演算子+は上部2つを取出し
int r = pop() ;
int l = pop() ;
// 加算結果をスタックに積む
push( l + r ) ;
} else if ( *p == '*' ) {
// 演算子*は上部2つを取出し
int r = pop() ;
int l = pop() ;
// 乗算結果をスタックに積む
push( l * r ) ;
}//~~~~~~~~~~~~~(B)
}
// 最終結果がスタックに残る
return pop() ;
}
void main() {
printf( "%d\n" , rpn( "123*+" ) ) ;
}
逆ポーランド記法の式の実行は、上記のようにスタックを用いると簡単にできる。このようなスタックと簡単な命令で複雑な処理を行う方法はスタックマシンと呼ばれる。Java のバイトコードインタプリタもこのようなスタックマシンである。
Cプログラママニア向けの考察
上記のプログラムでは、int r=pop();…push(l+r); で記載しているが、
push( pop() + pop() ) ;とは移植性を考慮して書かなかった。理由を述べよ。
最初の関数電卓
初期の関数電卓では複雑な数式を計算する際に、演算子の優先順位を扱うのが困難であった。このため、HP社の関数電卓では、式の入力が RPN を用いていた。(HP-10Cシリーズ)
2項演算と構文木
演算子を含む式が与えられたとして、それを保存する場合、演算式の2分木で扱うと都合が良い。
+ / \ 1 * / \ 2 3
演算子の木のノードで、末端は数値であることに注目し、右枝・左枝がNULLなら数値(data部にはその数値)、それ以外は演算子(data部には演算子の文字コード)として扱うとして…
struct Tree {
int data ;
struct Tree* left ;
struct Tree* right ;
} ;
struct Tree* tree_int( int x ) // 数値のノード
{
struct Tree* n ;
n = (struct Tree*)malloc( sizeof( struct Tree ) ) ;
if ( n != NULL ) {
n->data = x ;
n->left = n->right = NULL ;
}
return n ;
}
struct Tree* tree_op( int op , // 演算子のノード
struct Tree* l , struct Tree* r ) {
struct Tree* n ;
n = (struct Tree*)malloc( sizeof( struct Tree ) ) ;
if ( n != NULL ) { // ~~~~~~~~~~~~~~~~~~~~~(C)
n->data = op ;
n->left = l ;
n->right = r ;
}
return n ;
}
// 与えられた演算子の木を計算する関数
int eval( struct Tree* p ) {
if ( p->left == NULL && p->right == NULL ) {
// 数値のノードは値を返す
return p->data ;
} else {
// 演算子のノードは、左辺値,右辺値を求め
// その計算結果を返す
switch( p->data ) {
case '+' : return eval( p->left ) + eval( p->right ) ;
case '*' : return eval( p->left ) * eval( p->right ) ;
} // ~~~~~~~~~~~~~~~(D) ~~~~~~~~(E)
}
}
void main() {
struct Tree* exp = // 1+(2*3) の構文木を生成
tree_op( '+' ,
tree_int( 1 ) ,
tree_op( '*' ,
tree_int( 2 ) , tree_int( 3 ) ) ) ;
printf( "%d¥n" , eval( exp ) ) ;
}
理解度確認
- 上記プログラム中の(A),(B),(C),(D)の型を答えよ。
const char*s, char* const sの違い
専攻科実験のサンプルコードで、警告がでたことについて質問があったので説明。
(( サンプルコード sample.cxx ))
#include <stdio.h>
void foo( char* s ) {
printf( "%s¥n" , s ) ;
}
int main() {
foo( "ABC" ) ;
return 0 ;
}
(( コンパイル時の警告 ))
$ g++ sample.cxx
test.cxx:6:6: warning: conversion from string literal
to 'char *' is deprecated
[-Wc++11-compat-deprecated-writable-strings]
foo( "abcde" ) ;
^
1 warning generated.
警告を抑止する “-Wno-…” のオプションをつけて “g++ -Wno-c++11-compat-deprecated-writable-strings sample.cxx” でコンパイルすることもできるけど、ここは変数の型を厳格にするのが鉄則。
この例では、引数の “ABC” が書き換えのできない定数なので、const キーワードを付ければよい。ただし、宣言時の const の付け場所によって、意味が違うので注意が必要。
void foo( char const* s ) { // const char* s も同じ意味 *s = 'A' ; // NG ポインタの先を書き換えできない s++ ; // OK ポインタを動かすことはできる } void foo( char *const s ) { *s = 'A' ; // OK ポインタの先は書き込める s++ ; // NG ポインタは動かせない } void foo( char const*const s ) { *s = 'A' ; // NG ポインタの先を書き換えできない s++ ; // NG ポインタは動かせない }
const を書く場所は?
int const x = 123 , y = 234 ; の場合、yは定数だろうか?
(( おまけ ))
#include <stdio.h>
int main() {
int const x = 123 , y = 234 ; // x は定数だけど yは定数?
x++ ; // 予想通りエラー
y++ ; // yも定数なのでエラー
int const s = 345 , const t = 456 ; // sもtも明らかに定数っぽい
// ^ここで文法エラー
// おまけのおまけ
char* s , t ; // s は文字へのポインタ、t は文字
char *s , *t ; // s は文字へのポインタ、t も文字へのポインタ
return 0 ;
}