創造工学演習発表会
創造工学演習
- 07/30 (不明飛行物捕手) UFOキャッチャーのシミュレータをUnityで作成。UFOキャッチャーの有名な技をいくつか実践できることを目指した。(UFOキャッチャーに3000円ツッコム想定でレベル変化。俺は500円以上ツッコンだことない) #創造工学演習
- 07/30 (不明飛行物捕手) UFOキャッチャーのシミュレータ #創造工学演習 https://twitter.com/TohruSaitoh/status/1…
- 07/30 (Typing. edu) タイピング練習とプログラミングのためのタイピング? もう少しプログラミングの言語をイメージした練習ワードをでるようにして欲しかったり。でもこれは情報系ジジイ教員の感想ね。 #創造工学演習
- 07/30 (sin Go!!) 信号はsignalとかsignだしsign(しん)go(ごー)じゃね? #創造工学演習
- 07/30 (sin Go!!) 運転支援で信号の変化を予測できないか…。信号情報はVICSから取得したいが、そのハードは開発困難で想定データを受信できたとしてシステム構築。データが公開されている地域も限定的なのでデータフォーマットなども想定で作らざるおえなかったみたい。 #創造工学演習
- 07/30 (sin Go!!) #創造工学演習 https://twitter.com/TohruSaitoh/status/1…
- 07/30 (ideal idea) アイデア発想の支援するために、曼荼羅法などの機能を実装。関連ワードの検索で支援。検索結果の内容を評価ができれば高評価だけど…。関連ワード検索などは動くけど複数人の利用を想定したセッション管理は未実装かな。 #創造工学演習
- 07/30 (ideal idea) #創造工学演習 https://twitter.com/TohruSaitoh/status/1…
- 07/30 (UnEI-C) 学祭の運営の支援システム構築。発表がソフトコンペのような丁寧なアイデア提案型で始まったけど、全般にわたるいい説明ですな。1人説明だけどな。支援のためのページを簡単生成できるような自動化について議論が欲しかった。 #創造工学演習
- 07/30 (UnEI-C) #創造工学演習 https://twitter.com/TohruSaitoh/status/1…
- 07/30 質問者から「実際にお客さんにサービス提供したとして幾ら?」との質問。シビアな質問だけど、先日訪問した情報・経営システム工学課程なら、定番の質問だろうな。ま、本科4年では意識を持てるだけで充分。 #創造工学演習
- 07/30 →ALL 自分たちで作ったもの写メってTweetしたかぁ?? #創造工学演習
- 07/30 (忘れ物防止) RFIDで忘れ物防止システムの構築。発表は実装重視型かな。個人的には好きだけどね。グループで作るネタをうまく配分してたかな。 #創造工学演習
- 07/30 (忘れ物防止) #創造工学演習 https://twitter.com/TohruSaitoh/status/1…
- 07/30 (ceries) 複数の希望に応じた候補のランキングなどのアルゴリズムの説明が欲しい。Instagram連携にチャレンジしているのは女の子らしくってGoodだけど、そこは未完か…残念。 #創造工学演習
- 07/30 (ceries) 週末デートをどうするか支援するアプリだとぉ〜。非リア充は土日は引きこもりなんだよ。 #創造工学演習
- 07/30 (TCMS) 注文までのインタフェースは基本が完成していた。作るメニューの画面を写真とテキストを与えたら自動生成するなどの対応を期待。発注の流れをメールに割り切ったのは基本機能を完成させる点でアリかな。 #創造工学演習
- 07/30 (競技部門) 敵の行動予測をしたい,先の手をもっと読ませたいとの目標だけど、同じじゃ無いか? 領域ポイントの戦略がこのゲームの面白さなので、フィールドスカスカのターン数のはず。スカスカな状態で終わるターン数でもっと戦略を試してほしい。 #創造工学演習
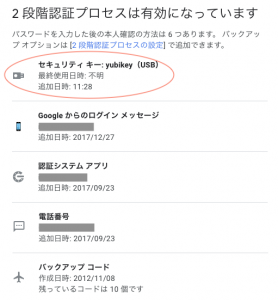
2段階認証用USBセキュリティキー
Office365で、パスワードが破られspamメール送信に利用される事案が発生している。
こういうパスワードへの攻撃には2段階認証が有効。私もSMSへの使い捨ての数字パスワードや、認証アプリを使ったりしている。でも最近では、なりすましサイトを挟んで使い捨て数字パスワードを盗む手法も出てきているので注意が必要。この中で最近注目されているのが、物理的キーを使うもの。Google では、全社員がこれを使うことで被害を防いでいるらしい。
以下は、YubiKey というFIDO対応のUSBキー。認証時に、パソコンのUSBキーに刺して、真ん中のボタンに触れるだけで認証が完了する。ただ、ChromeなどのFIDO対応のブラウザが必要らしい。

購入してから、あまり使ってこなかったけど、Google や Facebook は FIDO の認証に対応してきたようなので、設定してみた。
情報制御基礎2019全講義録
3年学際科目・情報制御基礎の2019年度の講義録の一覧
オブジェクト指向とソフトウェア工学
オブジェクト指向プログラミングの最後の総括として、 ソフトウェア工学との説明を行う。
トップダウン設計とウォーターフォール型開発
ソフトウェア工学でプログラムの開発において、一般的なサイクルとしては、 専攻科などではどこでも出てくるPDCAサイクル(Plan, Do, Check, Action)が行われる。 この時、プログラム開発の流れとして、大企業でのプログラム開発では一般的に、 トップダウン設計とウォーターフォール型開発が行われる。
トップダウン設計では、全体の設計(Plan)を受け、プログラムのコーディング(Do)を行い、 動作検証(Check)をうけ、最終的に利用者に納品し使ってもらう(Action)…の流れで開発が行われる。設計の中身も機能仕様や動作仕様…といった細かなフェーズになることも多い。 この場合、コーディングの際に設計の不備が見つかり設計のやり直しが発生すれば、 全行程の遅延となることから、前段階では完璧な設計が必要となる。 このような、上位設計から下流工程にむけ設計する方法は、トップダウン設計などと呼ばれる。また、処理は前段階へのフィードバック無しで次工程へ流れ、 川の流れが下流に向かう状態にたとえ、ウォーターフォールモデルと呼ばれる。

引用:Think IT 第2回開発プロセスモデル
このウォーターフォールモデルに沿った開発では、横軸時間、縦軸工程とした ガントチャートなどを描きながら進捗管理が行われる。

引用:Wikipedia ガントチャート
一方、チェック工程(テスト工程)では、 要件定義を満たしているかチェックしたり、設計を満たすかといったチェックが存在し、 テストの前工程にそれぞれ対応した機能のチェックが存在する。 その各工程に対応したテストを経て最終製品となる様は、V字モデルと呼ばれる。
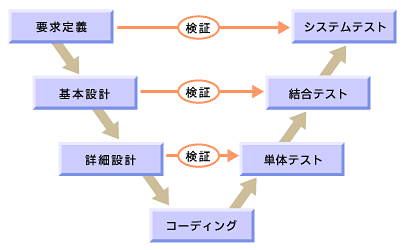
引用:@IT Eclipseテストツール活用の基礎知識
しかし、ウォーターフォールモデルでは、(前段階の製作物の不備は修正されるが)前段階の設計の不備があっても前工程に戻るという考えをとらないため、全体のPDCAサイクルが終わって次のPDCAサイクルまで問題が残ってしまう。巨大プロジェクトで大量の人が動いているだから、簡単に方針が揺らいでもトラブルの元にしかならないことから、こういった手法は大人数巨大プロジェクトでのやり方である。
ボトムアップ設計とアジャイル開発
少人数でプログラムを作っている時(あるいはプロトタイプ的な開発)には、 部品となる部分を完成させ、それを組合せて全体像を組み上げる手法もとられる。 この方法は、ボトムアップ設計と呼ばれる。このような設計は場当たり的な開発となる場合があり設計の見直しも発生しやすい。
また、ウォーターフォールモデルでは、前工程の不備をタイムリーに見直すことができないが、 少人数開発では適宜前工程の見直しが可能となる。 特にオブジェクト指向プログラミングを実践して隠蔽化が正しく行われていれば、 オブジェクト指向によるライブラリの利用者への影響を最小にしながら、ライブラリの内部設計の見直しも可能となる。 このような外部からの見た挙動を変えることなく内部構造の改善を行うことはリファクタリングと呼ばれる。
一方、プログラム開発で、ある程度の規模のプログラムを作る際、最終目標の全機能を実装したものを 目標に作っていると、全体像が見えずプログラマーの達成感も得られないことから、 機能の一部分だけ完成させ、次々と機能を実装し完成に近づける方式もとられる。 この方式では、機能の一部分の実装までが1つのPDCAサイクルとみなされ、 このPDCAサイクルを何度も回して機能を増やしながら完成形に近づける方式とも言える。 このような開発方式は、アジャイルソフトウェア開発と呼ぶ。 一つのPDCAサイクルは、アジャイル開発では反復(イテレーション)と呼ばれ、 短い開発単位を繰り返し製品を作っていく。この方法では、一度の反復後の実装を顧客に見てもらい、 顧客とプログラマーが一体となって開発が行われる。
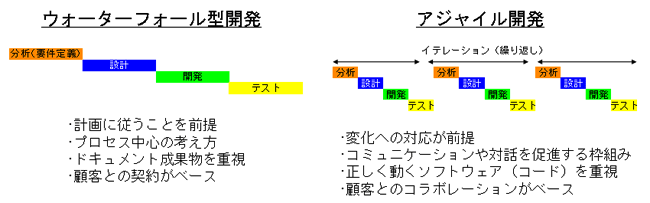
引用:コベルコシステム
エクストリームプログラミング
アジャイル開発を行うためのプログラミングスタイルとして、 エクストリームプログラミング(Xp)という考え方も提唱されている。 Xpでは、5つの価値(コミュニケーション,シンプル,フィードバック,勇気,尊重)を基本とし、 開発のためのプラクティス(習慣,実践)として、 テスト駆動開発(コーディングでは最初に機能をテストするためのプログラムを書き、そのテストが通るようにプログラムを書くことで,こまめにテストしながら開発を行う)や、 ペアプログラミング(2人ペアで開発し、コーディングを行う人とそのチェックを行う人で役割分担をし、 一定期間毎にその役割を交代する)などの方式が取られることが多い。
リーンソフトウェア開発は、品質の良いものを作る中で無駄の排除を目的とし、本当にその機能は必要かを疑いながら、優先順位をつけ実装し、その実装が使われているのか・有効に機能しているのかを評価ながら開発をすすめる。
伽藍(がらん)とバザール
これは、通常のソフトウェア開発の理論とは異なるが、重要な開発手法の概念なので「伽藍とバザール」を紹介する。
伽藍(がらん)とは、優美な寺院のことであり、その設計・開発は、優れた設計・優れた技術者により作られた完璧な実装を意味している。バザールは有象無象の人の集まりの中で作られていくものを意味している。
たとえば、伽藍方式の代表格である Microsoft の製品は、優秀なプロダクトだが、中身の設計情報などを普通の人は見ることはできない。このため潜在的なバグが見つかりにくいと言われている。これに対しバザール方式の代表格の Linux は、インターネット上にソースコードが公開され、誰もがソースコードに触れプログラムを改良してもいい。その中で、新しい便利な機能を追加しインターネットに公開されれば、良いコードは生き残り、悪いコードは淘汰されていく。
バザール方式は、オープンソースライセンスにより成り立っていて、このライセンスが適用されていれば、改良した機能はインターネットに公開する義務を引き継ぐ。このライセンスの代表格が、GNU パブリックライセンス(GPL)であり、公開の義務の範囲により、BSD ライセンス、Apacheライセンスといった違いがある。


集合とリスト処理
リスト構造は、必要に応じてメモリを確保するデータ構造であり、データ件数に依存しないプログラム が記述できる。その応用として、集合処理を考えてみる。
2進数を用いた集合計算
リストによる集合の前に、もっと簡単な集合処理を考える。データ件数の上限が少ない場合には、「2進数の列」の各ビットを集合の各要素に対応づけし、要素の有無を0/1で表現する。この方法を用いるとC言語のビット演算命令で 和集合、積集合を計算できるので、処理が極めて簡単になる。
以下のプログラムは、0〜31の数字を2進数の各ビットに対応付けし、 ba = {1,2,3} , bb = {2,4,6} , bc= {4,6,9} を要素として持つ集合で、ba ∩ bb , bb ∩ bc , ba ∪ bc の計算を行う例である。
// 符号なし整数を uint_t とする。
typedef unsigned int uint_t ;
// uint_tのbit数
#define UINT_BITS (sizeof( uint_t ) * 8)
// 集合の内容を表示
void bit_print( uint_t x ) {
for( int i = 0 ; i < UINT_BITS ; i++ )
if ( (x & (1 << i)) != 0 )
printf( "%d " , i ) ;
printf( "\n" ) ;
}
void main() { // 98,7654,3210
// ba = {1,2,3} = 00,0000,1110
uint_t ba = (1<<1) | (1<<2) | (1<<3) ;
// bb = {2,4,6} = 00,0101,0100
uint_t bb = (1<<2) | (1<<4) | (1<<6) ;
// bc = {4,6,9} = 10,0101,0000
uint_t bc = (1<<4) | (1<<6) | (1<<9) ;
bit_print( ba & bb ) ; // ba ∩ bb = {2}
bit_print( bb & bc ) ; // bb ∩ bc = {4,6}
bit_print( ba | bc ) ; // ba ∪ bc = {1,2,3,4,6,9}
}
このような、2進数を用いた処理で有名なものとして、エラトステネスのふるいによる素数計算がある。このアルゴリズムでは、各bitを整数に対応付けし、素数で無いと判断した2進数の各桁に1の目印をつけていく方式である。
uint_t prime = 0 ; // 初期値=すべての数は素数とする。
void filter() {
for( int i = 2 ; i < UINT_BITS ; i++ ) {
if ( (prime & (1 << i)) == 0 ) {
// iの倍数には、非素数の目印(1)をつける
for( int j = 2*i ; j < UINT_BITS ; j += i )
prime |= (1 << j) ;
}
}
for( int i = 2 ; i < UINT_BITS ; i++ ) {
// 目印のついていない数は素数
if ( (prime & (1 << i)) == 0 )
printf( "%d\n" , i ) ;
}
}
リスト処理による積集合
前述の方法は、リストに含まれる/含まれないを、2進数の0/1で表現する方式である。しかし、2進数であれば、unsigned int で 32要素、unsigned long long int で 64 要素が上限となってしまう。 (32bitコンピュータ,gccの場合)
しかし、リスト構造であれば、リストの要素として扱うことで、要素件数は自由に扱える。また、今までの授業で説明してきた cons() などを使って表現すれば、簡単なプログラムでリストの処理が記述できる。
// 先週までに説明してきたリスト構造と補助関数
struct List {
int data ;
struct List* next ;
} ;
struct List* cons( int x , struct List* n ) {
struct List* ans ;
ans = (struct List*)malloc( sizeof( struct List ) ) ;
if ( ans != NULL ) {
ans->data = x ;
ans->next = n ;
}
return ans ;
}
void print( struct List* p ) {
for( ; p != NULL ; p = p->next ) {
printf( "%d " , p->data ) ;
}
printf( "\n" ) ;
}
int find( struct List* p , int key ) {
for( ; p != NULL ; p = p->next )
if ( p->data == key )
return 1 ;
return 0 ;
}
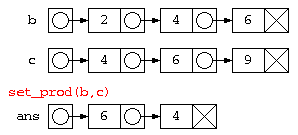
例えば、積集合(a ∩ b)を求めるのであれば、リストa の各要素が、リストb の中に含まれるか find 関数でチェックし、 両方に含まれたものだけを、ans に加えていく…という考えでプログラムを作ると以下のようになる。
// 集合積の計算
struct List* set_prod( struct List* a , struct List* b ) {
struct List* ans = NULL ;
for( ; a != NULL ; a = a->next ) {
// aの要素がbにも含まれていたら、ansに加える
if ( find( b , a->data ) )
ans = cons( a->data , ans ) ;
}
return ans ;
}
void main() {
struct List* a = cons( 1, cons( 2, cons( 3, NULL ) ) ) ;
struct List* b = cons( 2, cons( 4, cons( 6, NULL ) ) ) ;
struct List* c = cons( 4, cons( 6, cons( 9, NULL ) ) ) ;
print( set_prod( a , b ) ) ;
print( set_prod( b , c ) ) ;
}
例題として、和集合、差集合などを考えてみよう。
リストの共有と削除の問題
リスト処理では、mallocを使うが、メモリリークをさせないためには、使用後のリストの廃棄は重要である。リストの全要素を捨てる処理であれば、以下のようになるであろう。
void list_free( struct List* p ) {
while( p != NULL ) {
struct List* d = p ;
p = p->next ;
free( d ) ; // 順序に注意
}
}
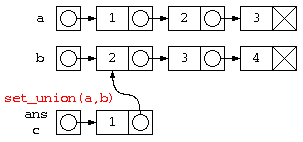
一方、前説明の和集合(a ∪ b)のプログラムを以下のように作った場合、list_freeの処理は問題となる。
// 集合和
struct List* set_union( struct List*a, struct List*b ) {
struct List* ans = b ;
for( ; a != NULL ; a = a->next )
if ( !find( b , a->data ) )
ans = cons( a->data , ans ) ;
return ans ;
}
void main() {
struct List*a = cons( 1, cons( 2, cons( 3, NULL ) ) ) ;
struct List*b = cons( 2, cons( 3, cons( 4, NULL ) ) ) ;
struct List*c = set_union( a , b ) ;
// a,b,cを使った処理
// 処理が終わったので、a,b,cを捨てる
list_free( a ) ;
list_free( b ) ;
list_free( c ) ;
// c = { 1 , (bのリスト) }
// (b)の部分は先のlist_free(b)で解放済み
}
このような、リストb,リストcで共有されている部分があると、データの廃棄処理をどのように記述すべきなのか、問題となる。
これらの解決方法としては、(1) set_union() の最初で、ans=b となっている部分を別にコピーしておく、(2) 参照カウンタ法を用いる、(3) ガベージコレクタのある言語を用いる…などがある。(2),(3)は後期授業で改めて解説を行う。
// 同じ要素を含む、新しいリストを作る struct List* copy( struct List*p ) { struct List*ans = NULL ; for( ; p != NULL ; p = p->next ) ans = cons( p->data , ans ) ; return ans ; } struct List* set_union( struct List*a, struct List* b ) { struct List* ans = copy( b ) ; // この後は自分で考えよう。 }
理解確認
- 2進数を用いた集合処理は、どのように行うか?
- リスト構造を用いた集合処理は、どのように行うか?
- 積集合(A ∩ B)、和集合(A ∪ B)、差集合(A – B) の処理を記述せよ。
スタックと待ち行列
計算処理中に一時的なデータの保存として、stackとqueueがよく利用されるが、それを配列を使って記述したり、任意の大きさにできるリストを用いて記述する。
# 授業は、前回の演習時間が不十分だったので、前半講義、後半演習時間。
スタック
配列を用いたスタック
一時的な値の記憶によく利用されるスタックは、一般的にLIFO( Last In First out )と呼ばれる。配列を使って記述すると以下のようになるであろう。
#define STACK_SIZE 32
int stack[ STACK_SIZE ] ;
int sp = 0 ;
void push( int x ) { // データをスタックに積む
stack[ sp++ ] = x ;
}
int pop() { // スタックのてっぺんを取り出す
return stack[ --sp ] ;
}
void main() {
push( 1 ) ; push( 2 ) ; push( 3 ) ;
printf( "%d\n" , pop() ) ; // 3
printf( "%d\n" , pop() ) ; // 2
printf( "%d\n" , pop() ) ; // 1
}
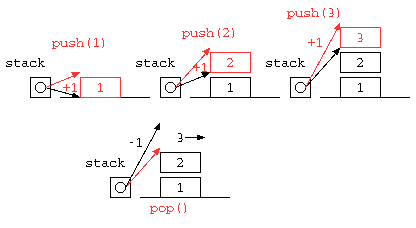
++,–の前置型と後置型の違い
// 後置インクリメント演算子 int i = 100 ; printf( "%d" , i++ ) ; // これは、 printf( "%d" , i ) ; i++ ; // と同じ。100が表示される。 // 前置インクリメント演算子 int i = 100 ; printf( "%d" , ++i ) ; // これは、 i++ ; printf( "%d" , i ) ; // と同じ
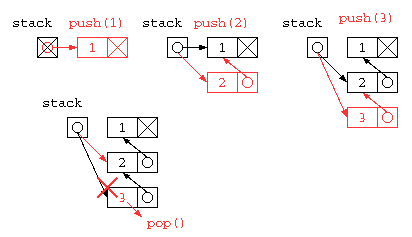
リスト構造を用いたスタック
しかし、この中にSTACK_SIZE以上のデータは貯えられない。同じ処理をリストを使って記述すれば、ヒープメモリを使い切るまで使うことができるだろう。
struct List* stack = NULL ;
void push( int x ) { // リスト先頭に挿入
stack = cons( x , stack ) ;
}
int pop() { // リスト先頭を取り出す
int ans = stack->data ;
struct List* d = stack ;
stack = stack->next ;
free( d ) ;
return ans ;
}
キュー(QUEUE)
2つの処理の間でデータを受け渡す際に、その間に入って一時的にデータを蓄えるためには、待ち行列(キュー)がよく利用される。 FIFO(First In First Out)
配列を用いたQUEUE / リングバッファ
配列にデータを入れる場所(wp)と取り出す場所のポインタ(rp)を使って蓄えれば良いが、配列サイズを超えることができないので、データを取り出したあとの場所を循環して用いるリングバッファは以下のようなコードで示される。
#define QUEUE_SIZE 32
int queue[ QUEUE_SIZE ] ;
int wp = 0 ; // write pointer(書き込み用)
int rp = 0 ; // read pointer(読み出し用)
void put( int x ) { // 書き込んで後ろ(次)に移動
queue[ wp++ ] = x ;
if ( wp >= QUEUE_SIZE ) // 末尾なら先頭に戻る
wp = 0 ;
}
int get() { // 読み出して後ろ(次)に移動
int ans = queue[ rp++ ] ;
if ( rp >= QUEUE_SIZE ) // 末尾なら先頭に戻る
rp = 0 ;
return ans ;
}
void main() {
put( 1 ) ; put( 2 ) ; put( 3 ) ;
printf( "%d\n" , get() ) ; // 1
printf( "%d\n" , get() ) ; // 2
printf( "%d\n" , get() ) ; // 3
}
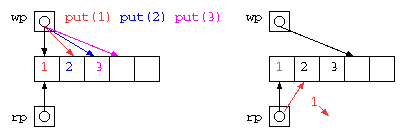
このようなデータ構造も、get() の実行が滞るようであれば、wp が rp に循環して追いついてしまう。
リスト構造を用いたQUEUE
そこで、このプログラムもリストを使って記述すると以下のようになる。
struct List* queue = NULL ;
struct List** tail = &queue ;
void put( int x ) { // リスト末尾に追加
*tail = cons( x , NULL ) ;
tail = &( (*tail)->next ) ;
}
int get() { // リスト先頭から取り出す
int ans = queue->data ;
struct List* d = queue ;
queue = queue->next ;
free( d ) ;
return ans ;
}
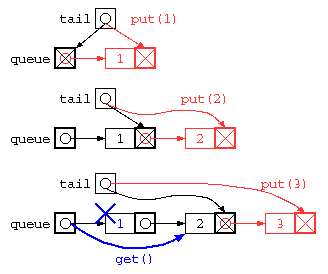
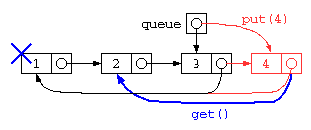
ただし、上記のプログラムは、データ格納後にget()で全データを取り出してしまうと、tail ポインタが正しい位置になっていないため、おかしな状態になってしまう。
また、このプログラムでは、rp,wp の2つのポインタで管理することになるが、 2重管理を防ぐために、リストの先頭と末尾を1つのセルで管理する循環リストが使われることが多い。
理解確認
- 配列を用いたスタック・待ち行列は、どのような処理か?図などを用いて説明せよ。
- リスト構造を用いたスタック・待ち行列について、図などを用いて説明せよ。
- スタックや待ち行列を、配列でなくリスト構造を用いることで、どういう利点があるか?欠点があるか説明せよ。
MySQLでトラブル対応
仕事で動かしているサーバが動いていないとの連絡が入り、システムが動いていない。
他の方との共同のネタなので、サーバーの更新は慎重に行っているけど、今回は MySQL が落ちているのが原因。サーバーの定期的な更新作業後あたりから動かなくなっているので、最近更新されたパッケージを確認し、MySQL が含まれていたのでパッケージを一つ前のバージョンに落とそうと対応を行った。
しかしダウングレードでパッケージの不整合が出る中、無理やりダウングレードをおこなって MySQL を起動させようとするが、”mysqld got signal 11 ; This could be because you hit a bug.” といったメッセージで起動しない。
四苦八苦するも原因がつかめず、以前の状態に戻そうとバックアップ時に作成しておいたパッケージのバージョン情報を確認すると、パッケージが更新されて動かなくなったのではなく、パッケージが消されていたことが判明。原因を誤解していた。
OSの更新作業の中で、MySQL のメジャー更新で使っていたバージョンが標準パッケージから外されたみたい。メジャー更新すればいいのだろうけど、運用不安もあるので、MySQL の本家で公開しているパッケージを入れて、無事復旧。
長期運用とはいえ、更新は慎重に作業せねば。
差分とフィードバック制御
情報制御基礎の授業を通して、入力値を制御するため、コンピュータを使う場合の数値処理の基礎的な話として、信号の平滑化を説明してきたので、最後に差分について説明をする。また、実際には、入力値を制御に利用する一般的な構成のフィードバック制御について説明する。
変化の検出
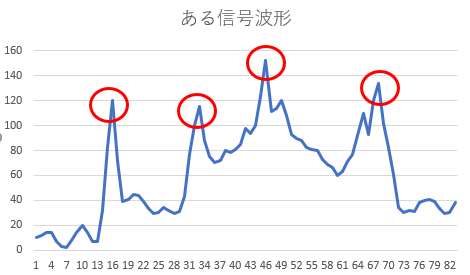
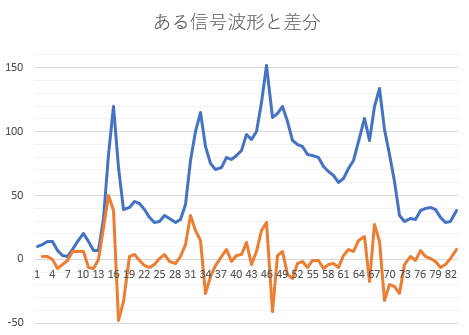
例えば、以下のような若干のノイズが混ざった入力信号が与えられたとする。この波形で「大きな山が何ヶ所ありますか?」と聞かれたら、いくつと答えるべきであろうか?山の判断方法は色々あるが、4カ所という答えは、1つの見方であろう。では、この4カ所という判断はどうすればいいだろうか?
こういった山の数を数えるのであれば、一定値より高いか低いか…という判断方法もあるだろう。この絵であれば、15ステップ目、32ステップ目付近は、100を越えていることで、2つの山と判断できるだろう。
こういった予め決めておいた値より「上か?/下か?」で判断するときの基準値は、しきい値(閾値)と呼ぶ。
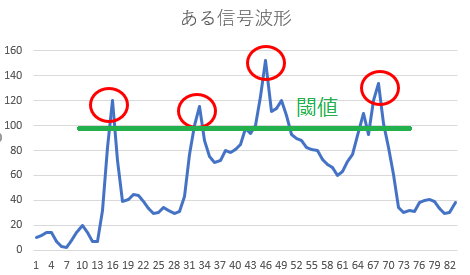
しかし、この閾値では、40ステップ目から50ステップ目も100を越えており、以下のようなプログラムを書いたら、40ステップ目~50ステップ目すべてをカウントしてしまう。
#define THRESHOLD 100
int x[ 100 ] = {
// 波形のデータが入っているとする。
} ;
int count = 0 ;
for( int i = 0 ; i < 100 ; i++ ) {
if ( x[i] >= THRESHOLD )
count++ ;
}
また、65ステップ目の小さな山も1個とカウントしてしまう。
この問題を避けるために、閾値を130にすると、今度は最初の2つの山をカウントできない。どうすれば、山の数をうまくカウントできるのだろうか?
差分を求める
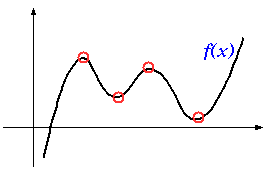
前述のような問題で山の数を数える方法を考えていたが、数学で山を見つける時には、何をするだろうか?
数学なら、山や谷の頂点を求めるのならば、微分して変化量が0となる場所を求めることで、極大値・極小値を求めるだろう。そこで、山を見つけるために入力値の変化量を求めてみよう。
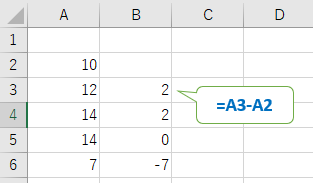
表計算ソフトで差分を計算するのであれば、セルに図のような式を入力すればいいであろう。このようなデータ点で前の値との差を差分と呼ぶ。数学であれば、微分に相当する。
このグラフを見ると、波形が大きく増加する部分で、差分が大きな正の値となる。さらに波形が大きく減少する部分で差分が負の大きな値となる。特にこのデータの場合、山と判断したい部分は差分が20以上の値の部分と定義することも考えられる。
#define TH_DIFF 20
int x[ 100 ] = {
// 波形のデータが入っているとする。
} ;
int count = 0 ;
for( int i = 0 ; i < 100 ; i++ ) {
if ( x[i] - x[i-1] >= TH_DIFF
&& x[i+1] - x[i] <= -TH_DIFF )
count++ ;
}
しかし、このプログラムでは、山の数をうまくカウントしてくれない。うまく、山の数を数えるためには、差分の値を山と判断するための閾値(この場合は20)を調整することになるだろう。
制御工学の概要
以下に、制御工学ではどのようなことを行うのか、概要を述べる。
ここで紹介する制御理論は、古典制御理論と呼ばれる。
制御工学では、入力値と、何らかの処理を施し出力値
が得られるシステムで、どのように制御するかを考える。
例えば、電気ポットの温度制御をする場合、設定温度の値を入力値とし、何らかの処理を行い、出力となるヒーターの電流を制御し、最終的には温度
が測定される。ヒーターは、設定温度
と温度計の値
の差
に応じて電流量を変化させる。このように一般的な制御では、最終的な温度が入力に戻っている。このように目標値に近づけるために、目標値との差に応じて制御することをフィードバック制御という。
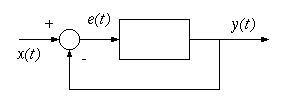
制御の仕方には様々な方法があるが、 がとある時間で0からYに変化した場合を考える。入力と出力で制御された波形の例を示す。
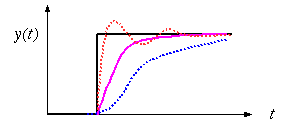
この波形では、黒のように入力値が変化した場合、それに追いつこうと出力が変化する。(1)理想的には、速やかに追いつく赤のように変化したい。しかし、(2)慎重に制御をする人なら、変化への制動が大きい過制動(青点線)となり、目標値に追いつくまでに時間がかかる。(3)一方、すこしでもずれたら直そうとする人なら、時間的には速い反応ができるかもしれないが、目標値を追い越したり、増えすぎ分を減らしすぎたりして脈動する過制御(赤点線)となるかもしれない。
PID制御
目標値、出力
、ずれ(偏差)
、制御量
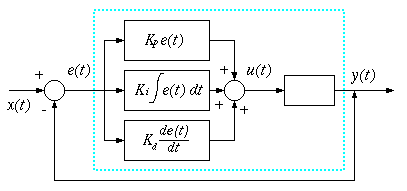
とした時、基本的なフィードバック制御として偏差の使い方によってP動作,I動作,D動作がある。参考 Wikipedia PID制御
比例制御(P制御)
偏差に比例した制御を行う方式(を比例ゲインと呼ぶ)
積分制御(I制御)
偏差のある状態が長い時間続く場合、入力値の変化を大きくすることで目標値に近づけるための制御。(は積分ゲイン)
微分制御(D制御)
急激な出力値の変化が起こった場合、その変化の大きさに応じて妨げようとする制御。(は微分ゲイン)
PID制御
上記のI制御やD制御だけでは、安定させることが難しいので、これらを組み合わせたPID制御を行う。
この中で、の値は、制御が最も安定するように調整を行うものであり、数値シミュレーションや、ステップ応答を与えた時の時間的変化を測定して調整を行う。
UML課題
期末試験も近いので、今後の日程の確認。
7/12 UMLレポート課題作成, 7/19 オブジェクト指向のソフトウェア工学, 7/26 課題作成
オブジェクト指向プログラミングの第3回レポート課題は、以下の通り。
特別研究や関連の内容でUMLを記述
専攻科の自分自身の特別研究での自身のプログラムをUMLで表現せよ。もしプログラム作成でない場合は、特別研究で行なっている実験方法とそのデータを UML で表現せよ。
- UMLとして表現する対象の説明として、レポートとして表現する部分の特別研究の内容を説明
- 扱うデータ構造などについて、UMLの構造図のうちの1つを選んでその構造図を示せ。またその構造図で表現した理由がわかるような説明をすること(is-a,has-aなど)
- その処理などについて、UMLの振る舞い図のうちの1つを選んで、その振る舞いを図で説明せよ。同じくその図について説明せよ