様々な移動平均
波形処理をハードウェアで行うかソフトウェアで行うか
組込み用の小型コンピュータが普及する以前は、このような波形に対する処理を行う場合には、電子回路的に波形のフィルタリングを行っていた。しかし電子回路的な方法では、回路の特性が変化してうまく処理ができなくなった場合に、回路の組み換えが発生するかもしれない。ただし回路の変更は基板の作り直しが必要であったりすることから、コストがかかる。
一方、A/D変換機能を内蔵した組込み用小型コンピュータも極めて安価になってきた。
こういったコンピュータの普及で、最近ではアナログ値をコンピュータに取り込んでデジタルの数値的な処理で余計な情報を取り除く。この方法であれば、プログラムを変更するだけなので、安価に変更が可能となる。ただし、アナログ値をA/D変換するのには時間がかかることから、周波数の高い信号には不向きである。
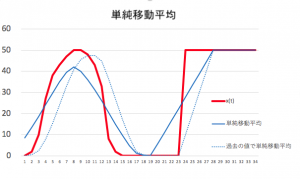
単純移動平均
前回説明を行った単純移動平均は、時刻tの平均を、その前後のデータで平均を求めた。この方式は、実際には与えられた波形のデータを全部記録した跡に、単純移動平均をとる場合に有効である。
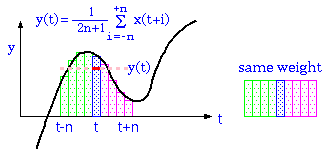
しかし、時々刻々変化する測定値の平均をその都度使うことを考えると、上記の方法は、未来の測定値
を使っていることから、現実的ではない。
#define NS 3
int x[ SIZE ] ; // 入力値
int y[ SIZE ] ; // 出力値
for( int t = NS ; t < SIZE-NS ; t++ ) {
int s = 0 ;
for( int i = -NS ; i <= +NS ; i++ ) // 2*NS+1回の繰り返し
s += x[t+i] ;
y[t] = s / (2*NS + 1) ;
}
過去の値だけを使った移動平均
そこで、過去の値だけで移動平均をとることも考えられる。
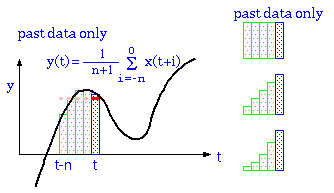
この、単純移動平均と、過去の値だけを使う単純移動平均を、適当な測定値に対して適用した場合のグラフの変化を Excel によってシミュレーションした結果を以下に示す。
しかし、このグラフを見ると、波形後半の部分に注目するとよく分かるが、過去の値だけを使った移動平均では、測定値が立ち上がったのを追いかけて値が増えていく。これでは移動平均は時間的な遅れとなってしまう。
for( int t = NS ; t < SIZE ; t++ ) {
int s = 0 ;
for( int i = 0 ; i <= NS ; i++ ) // NS+1回の繰り返し
s += x[t-i] ;
y[t] = s / (NS+1) ;
}
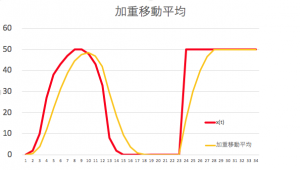
加重移動平均
過去の値を使った移動平均では遅れが発生する。でも、平均を取る際に、「n回前の値」と「現在の値」を考えた時、「その瞬間の平均値」は「現在の値」の方が近い値のはず。であれば、平均を取る時に、「n回前の値は少なめ」「現在の値は多め」に比重をかけて加算する方法がある。
for( int t = 3 ; t < SIZE ; t++ ) {
int s = x[t] * 3
+ x[t-1] * 2
+ x[t-2] * 1 ; // 数個の移動平均だし、
y[t] = s / (3+2+1) ; // ループを使わずに書いてみる。
}
この様に、過去に遡るにつれ、平均をとる比重を直線的に小さくしながら移動平均をとる方法は、加重移動平均と呼ばれる。以下にその変化をExcelでシミュレーションしたものを示す。
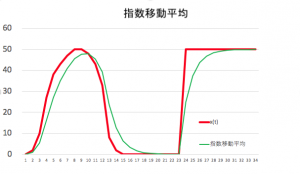
指数移動平均
ここまで説明してきた、単純移動平均や、加重移動平均は、平均をとる範囲の「過去の値」を記憶しておく必要がある。広い時間にわたる移動平均をとる場合は、それに応じてメモリも必要となる。これは、組み込み型の小型コンピュータであれば、メモリが足りず平均処理ができない場合もでてくる。
そこで、荷重移動平均の重みを、は、100%,
は50%,
は25%… というように、過去に遡るにつれ、半分にして平均をとる。
しかし、以降の項で、
を使うと以下のように書き換えることができる。
for( int t = 1 ; t < SIZE ; t++ ) {
y[t] = ( x[t] + y[t-1] ) / 2 ;
}
この方法であれば、直前の平均値を記録しておくだけで良い。このような移動平均を、指数移動平均と呼ぶ。
ここで示した指数移動平均は、過去を遡るにつれとなっているが、これをさらに一般化した指数移動平均は、以下の式で示される。前述の移動平均は、
とみなすことができる。
#define ALPHA 0.5
for( int t = 1 ; t < SIZE ; t++ ) {
y[t] = ALPHA * x[t] + (1.0 - ALPHA) * y[t-1] ;
}
以下のプログラムは、うまく動かない。理由を説明せよ。
#define RVA 4 for( int t = 1 ; t < SIZE ; t++ ) { // 以下はy[t]は全部ゼロになる。 y[t] = 1/RVA * x[t] + (1.0 - 1/RVA) * y[t-1] ; // 以下は、整数型演算だけで、正しく動くだろう。 // y[t] = ( x[t] + (RVA-1) * y[t-1] ) / RVA ; }
理解度確認のための小レポート
上記の移動平均の理解のために、以下の資料(講義では印刷資料を配布)の表の中を、電卓などを使って計算せよ。
計算したら、その結果をグラフの中にプロットし、どういった波形となるか確認し、レポートとして提出すること。
UML振る舞い図
参考資料図をもとに振る舞い図の説明を行う。
ユースケース図

ユーザなど外部からの要求に対する、システムの振る舞いを表現するための活用事例を表す図がユースケース図。 システムを構築する際に、最初に記述するUMLであり、システムに対する処理要件の全体像を理解するために記述する。 ユーザや外部のシステムは、アクターとよび人形の絵で示す。楕円でシステムに対する具体的な処理をユースケースとして記述する。 関連する複数のユースケースをまとめて、サブジェクトとして示す場合もある。
アクティビティ図
処理順序を記述するための図にはフローチャートがあるが、上から下に処理順序を記述するため、縦長の図になりやすい。また、四角枠の中に複雑なことを書けないので、UMLではアクティビティ図を用いる。
初期状態から、終了状態までの手順を示すためのがアクティビティ図。 複数の処理を並行処理する場合には、フォークノードで複数の処理を併記し、最終的に1つの処理になる部分をマージノードで示す。 通常の処理は、角丸の長方形で示し、条件分岐はひし形で示す。
ステートチャート図(状態遷移図)
ステートチャート図は、処理内部での状態遷移を示すための図。 1つの状態を長丸長方形で示し、初期状態から終了状態までを結ぶ。 1つの状態から、なんらかの状態で他の状態に遷移する場合は、分岐条件となる契機(タイミング)とその条件、およびその効果(出力)を「契機[条件]/効果」で矢印に併記する。 複数の状態をグループ化して表す場合もある。
シーケンス図
複数のオブジェクトが相互にやり取りをしながら処理が進むようなものを記述するためのものがシーケンス図。 上部の長方形にクラス/オブジェクトを示し、その下に時系列の処理の流れの線(Life Line)を描く。 オブジェクトがアクティブな状態は、縦長の長方形で示し、そのLife Line間を、やり取り(メッセージ)の線で相互に結ぶ。 メッセージは、相手側からの返答を待つような同期メッセージは、黒塗り三角矢印で示す。 返答を待たない非同期メッセージは矢印で示し、返答は破線で示す。
コミュニケーション図
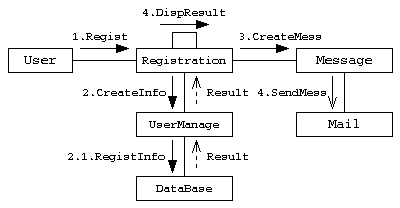
クラスやオブジェクトの間の処理とその応答(相互作用)と関連の両方を表現する図。
その他の構造図
前回の講義で説明した構造図について、クラス図・オブジェクト図以外について説明
構造図の主なものとして、クラス図、オブジェクト図以外に、
- パッケージ図(クラスなどをグループ化したパッケージの関係)
- コンポジット構造図(クラスやコンポーネントの内部構造を示す)
- コンポーネント図(コンポーネントの内部構造とコンポーネント間の依存関係)
- 配置図(システムの物理的な構成)
パッケージ図
パッケージ図は、クラス図をパッケージ毎に分類して記載する図。 パッケージの塊を、フォルダのような図で記載する。

IT専科から引用
コンポーネント図とコンポジット構造図
コンポーネント図は、複数のクラスで構成される処理に、 インタフェースを用意し、あたかも1つのクラスのように扱ったもの。 接続するインタフェースを、提供側を◯───で表し、要求側を⊃──で表す。
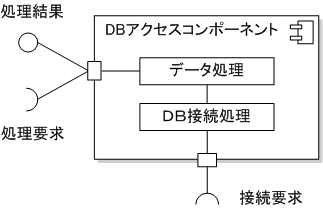
IT専科から引用
配置図
配置図は、システムのハードウェア構成や通信経路などを表現するための図。 ハードウェアは直方体の絵で表現し、 デバイスの説明は、”≪device≫”などを示し、実行環境には、”≪executionEnvironment≫” などの目印で表現する。
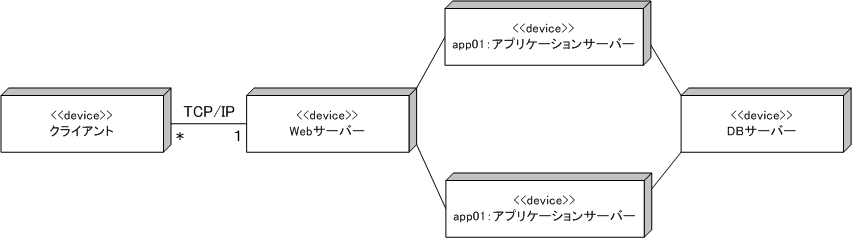
IT専科から引用