コンストラクタと複素数クラス
コンストラクタ
プログラミングでは、データの初期化忘れによる間違いもよく発生する。これを防ぐために、C++ のクラスでは、コンストラクタ(構築子)がある。データ構造の初期化専用の関数。
// コンストラクタ
#include <stdio.h>
#include <string.h>
class Person {
private:
char name[ 20 ] ;
int age ;
public:
void print() {
printf( "%s %d¥n" , name , age ) ;
}
Person() { // コンストラクタ(A)
name[0] = '¥0' ; // 空文字列
age = 0 ;
}
Person( const char str[] , int ag ) { // コンストラクタ(B)
strcpy( name , str ) ;
age = ag ;
}
~Person() { // デストラクタ
print() ; // 内容の表示
}
} ;
int main() {
Person saitoh( "t-saitoh" , 55 ) ; // (A)で初期化
Person tomoko() ; // (B)で初期化
saitoh.print() ; // "t-saitoh 55" の表示
tomoko.print() ; // " 0" の表示
return 0 ; // この時点で saitoh.~Person()
// tomoko.~Person() が自動的に
} // 呼び出される。
コンストラクタと反対に、デストラクタは、データが不要となった時に自動的に呼び出される関数。
このクラスの中には、引数無しのコンストラクタと、引数ありのコンストラクタが出てくる。C++では、同じ名前の関数でも引数の数や型に応じて呼出す関数を適切に選んでくれる。(関数のオーバーロード)
デストラクタは、データが不要となった時に自動的に呼び出してくれる関数で、一般的にはC言語でのファイルの fopen() , fclose() のようなものを使う処理で、コンストラクタで fopen() , デストラクタで fclose() を呼出すように使うことが多いだろう。同じように、コンストラクタで malloc() を呼出し、デストラクタで free() を呼出すというのが定番の使い方だろう。
複素数クラスの例
隠蔽化と基本的なオブジェクト指向の練習課題として、複素数クラスをあげる。ここでは、複素数の加算・乗算を例に説明をするので、減算・除算などの処理を記述することで、クラスの扱いに慣れてもらう。
直交座標系
#include <stdio.h>
#include <math.h>
// 直交座標系の複素数クラス
class Complex {
private:
double re ; // 実部
double im ; // 虚部
public:
void print() {
printf( "%lf + j%lf¥n" , re , im ) ;
}
Complex( double r , double i ) {
re = r ;
im = i ;
}
Complex() {
// デフォルトコンストラクタ
re = im = 0.0 ;
}
void add( Complex z ) {
// 加算は、直交座標系だと極めてシンプル
re = re + z.re ;
im = im + z.im ;
}
void mul( Complex z ) {
// 乗算は、直交座標系だと、ちょっと煩雑
double r = re * z.re - im * z.im ;
double i = re * z.im + im * z.re ;
re = r ;
im = i ;
}
double get_re() {
return re ;
}
double get_im() {
return im ;
}
double get_abs() { // 絶対値
return sqrt( re*re + im*im ) ;
}
double get_arg() { // 偏角
return atan2( im , re ) ;
}
} ; // ←何度も繰り返すけど、ここのセミコロン忘れないでね
int main() {
// 複素数を作る
Complex a( 1.0 , 2.0 ) ;
Complex b( 2.0 , 3.0 ) ;
// 複素数の計算
a.print() ;
a.add( b ) ;
a.print() ;
a.mul( b ) ;
a.print() ;
return 0 ;
}
極座標系
上記の直交座標系の Complex クラスは、加減算の関数は単純だけど、乗除算の関数を書く時には面倒になってくる。この場合、極座標系でプログラムを書いたほうが判りやすいかもしれない。
// 局座標系の複素数クラス
class Complex {
private:
double r ; // 絶対値 r
double th ; // 偏角 θ
public:
void print() {
printf( "%lf ∠ %lf¥n" , r , th / 3.14159265 * 180.0 ) ;
}
Complex() {
r = th = 0.0 ;
}
// 表面的には、同じ使い方ができるように
// 直交座標系でのコンストラクタ
Complex( double x , double y ) {
r = sqrt( x*x + y*y ) ;
th = atan2( y , x ) ; // 象限を考慮したatan()
}
// 極座標系だと、わかりやすい処理
void mul( Complex z ) {
// 極座標系での乗算は
r = r * z.r ; // 絶対値の積
th = th + z.th ; // 偏角の和
}
// 反対に、加算は面倒な処理になってしまう。
void add( Complex z ) {
; // 自分で考えて
}
//
double get_abs() {
return r ;
}
double get_arg() {
return th ;
}
double get_re() {
return r * cos( th ) ;
}
double get_im() {
return r * sin( th ) ;
}
} ; // ←しつこく繰り返すけど、セミコロン忘れないでね(^_^;
このように、プログラムを開発していると、当初は直交座標系でプログラムを記述していたが、途中で極座標系の方がプログラムが書きやすいという局面となるかもしれない。しかし、オブジェクト指向による隠蔽化を正しく行っていれば、利用者に影響なく「データ構造」や「その手続き(メソッド)」を書換えることも可能となる。
このように、プログラムをさらに良いものとなるべく書換えることは、オブジェクト指向ではリファクタリングと呼ぶ。
正しくクラスを作っていれば、クラス利用者への影響が最小にしながらリファクタリングが可能となる。
メソッドのプロトタイプ宣言
class 構文では、{} の中に、要素の定義や、メソッドの記述を行うと説明してきたが、メソッド内の処理が長い場合もある。
この時に、すべてを {} の中に書こうとすると、全体像が見渡せない。こういう時には、以下のように、メソッドのプロトタイプ宣言と、メソッドの実体の記述を別に記載する。
class Complex {
private:
double re , im ;
public:
Complex( double r , double i ) ; // メソッドのプロトタイプ宣言
void print() ;
} ;
// メソッドの実体
Complex::Complex( double r , double i ) {
re = r ;
im = i ;
}
void Complex::print() {
printf( "%lf + j %lf" , re , im ) ;
}
ゲッター/セッター (経験者向け解説)
それぞれのクラス宣言では、get_re() , get_im() , get_abs() , get_arg() というメソッドを記載した。このように記述しておくと、クラス外で re , im といったメンバを public 指定をせずに、リファクタリングしやすいクラスにすることができる。(re, im を public にしてしまうと、クラス外でオブジェクトへの代入が可能となる。)
PHPなどの private や public の機能のないオブジェクト指向言語では、get_xx() といった要素の参照しかできないメソッドを作ったうえで、クラス外でメンバ参照をしないというマナーを徹底させることで、public 機能の代用し、隠蔽化を徹底させることも多い。
この場合、参照専用の get_xx() と同じように、要素に値を設定するためのメソッド set_xx( 値… ) を作るとプログラムの意味が分かりやすくなる。こういったクラスの参照や代入のメソッドは、getter(ゲッター),setter(セッター)と呼ぶ。
ゲッターやセッターメソッドでは、要素を参照(あるいは代入)するだけといった極めて単純な関数を作ることになる。この場合、関数呼び出しの処理時間が無駄になる。この対処として、C++ には inline 関数機能がある。関数(メソッド)の前に、inline を指定すると、コンパイラは関数呼び出し用の命令を生成せず、それと同じ処理となる命令を埋め込んでくれる。(開いたサブルーチン)
class Complex {
private:
double re , im ;
public:
:
inline void get_re() {
return re ;
}
} ;
const 指定 (経験者向け解説)
C++ では、間違って値を書き換えるような処理を書けないようにするための、const 指定の機能がある。
void foo( const int x ) {
x++ ; // 定数を書き換えることはできない。
printf( "%d\n" , x ) ;
}
int main() {
const double pi = 3.141592 ;
// C言語で #define PI 3.141592 と同等
int a = 123 ;
foo( a ) ;
return 0 ;
}
前に説明した、getter メソッドは要素を参照するだけで、オブジェクトの中身が変化しない。逆に言えば、getter のメソッド内にはオブジェクトに副作用のある処理を書いてはいけない。こういった用途に、オブジェクトを変化させないメソッド宣言がある。先の、get_re() は、
class ... {
:
inline double get_re() const {
re = 0 ; // 文法エラー
return re ;
}
} ;
高専ワイヤレスIoT技術実証コンテスト

総務省主催の、地域における若手人材を活用した電波有効利用に資するIoT技術実証の円滑な実施のため、有効策を取りまとめていくことを目的とした事業の一環としてのコンテストが開催されます。
全国の高等専門学校(学生)を対象に、第5世代移動通信システム(5G)の特性を生かした技術及びワイヤレスIoT技術を活用することにより、地域における諸課題について、様々な分野や業種、自治体、地域等を巻き込んだ解決、あるいは新たなサービスの実現に繋がるようなアイデアを公募します。
授業アンケート結果(ぷちブルーな気分)
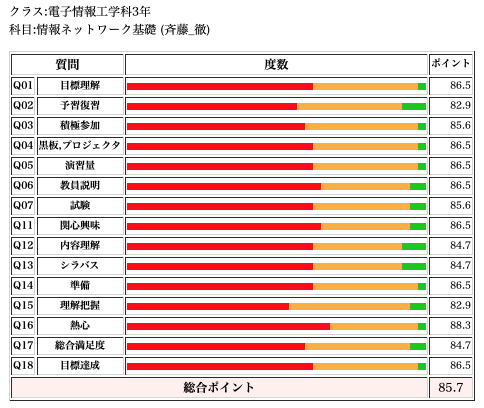
情報ネットワーク基礎(3EI/後期)
楽しんで受講してくれた人からの意見があり、ポイントでも85ポイントと高評価であった。内容理解やシラバスについてポイントが若干低いようであるが、誤差の範疇と思われる。理解把握のポイントが最も低く、理解度確認のための質問などをもう少し増やしても良かったかと思う。
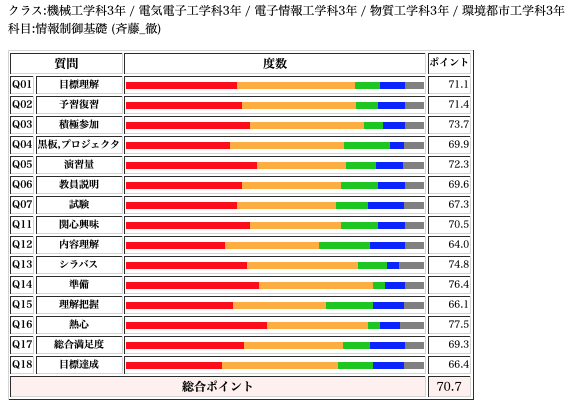
情報制御基礎(3年学際科目/前期)
学際科目ということで、初めて実施した科目であり、他学科からも受講生がある内容で、ポイントも70ポイントと低い評価であった。
プログラムを授業でやっていない学科の学生から、内容が理解できないとの意見が多かった。今年度は、他学科の学生にもわかるように、プログラムの説明を増やしたり、プログラムよりも基本的な内容を増やしたいと考えている。
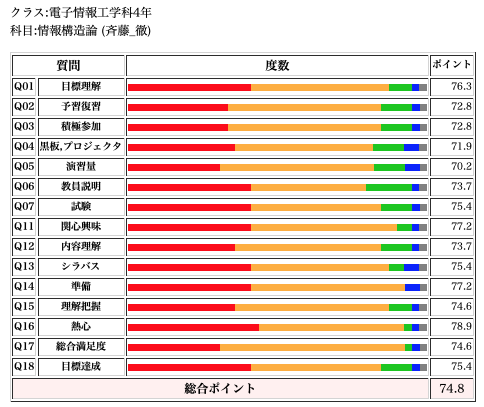
情報構造論(4EI/通年)
意見の欄には、例年になく辛辣な意見もあった。他の同クラスのアンケートでも、全般的に厳しい意見が多くみられ、ポイントは74.8と例年よりも低くいが、このクラスのオフセットとも考えられる。
昨年から講義資料のWeb掲載などを行い、それを使った授業を中心としているが、ノート作成ができていない学生から、ノートをとる時間を十分にとってほしいとの意見があった。もう少し、授業の時間の作り方などを考えたいが、一方で不まじめな学生がノートもも一切とらないで受講する姿は、理解する意欲に欠けていることもあり、どのような対処とすべきか、時間をかけて考えていきたい。
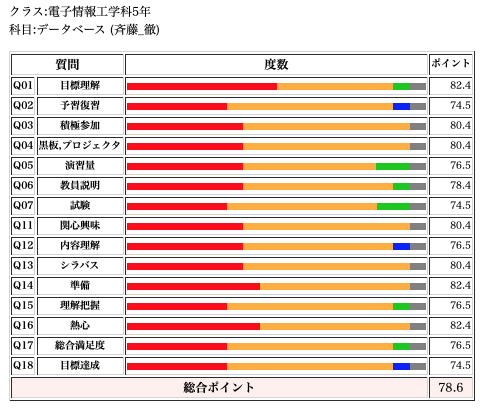
データベース(5EI/後期)
ポイントでは78.6と、若干低めの評価であった。演習量や試験についての評価が他に比べて若干低く、意見でも図や表といった具体例を交えた例での説明を増やしたほうが理解が進むとの建設的な意見もあった。資料などもWebでの公開などを進めているが、今後も実例などを増やし解りやすい資料を目指したい。
オブジェクト指向プログラミング(PS2/前期)
他学科出身の受講者も含まれるため、例年進度に注意しながら授業を進めているが、ポイントでは80ポイントで、例年並みの評価であった。
もう少し、演習などをタイムリーに行いながら授業を進めたいと考えているが、演習環境などの準備も必要で自主学習などの課題を検討したいと思う。
予備実験2 パズル問題
プログラミングコンテストの競技部門では、パズルのような組み合わせ問題が 出題されることが多い。そこで、この予備実験では、きわめて単純なパズル問題(組み合わせ問題) のプログラムについて扱う。
組み合わせ問題の基礎
簡単な問題として、「100未満の整数の値を3つ選び、その値を辺の長さとした場合、 直角三角形となるものをすべて表示する。」について考える。
一番簡単な方法は、以下となるであろう。
#include <stdio.h>
#include <math.h>
#include <time.h>
// 整数比の直角三角形の一覧を求める。
void integer_triangle( int n ) {
for( int a = 1 ; a < n ; a++ ) {
for( int b = 1 ; b < n ; b++ ) {
// 一番ダサい方法
for( int c = 1 ; c < n ; c++ ) {
if ( a*a + b*b == c*c ) {
printf( "%d %d %d\n" , a , b , c ) ;
}
}
}
}
}
int main() {
integer_triangle( 100 ) ;
return 0 ;
}
しかしこのプログラムの欠点としては、100×100×100回のループで無駄な処理が多い。
ループ回数を減らすだけなら、最も内側の処理を、計算で整数値か確認すればいい。
void integer_triangle( int n ) {
for( int a = 1 ; a < n ; a++ ) {
for( int b = 1 ; b < n ; b++ ) {
// ココも改良できるよね?
int d = a*a + b*b ;
int c = (int)sqrt( d ) ;
// 斜辺Cの整数値を求め、改めて確認する。
if ( c*c == d ) {
printf( "%d %d %d\n" , a , b , c ) ;
}
}
}
}
(1) 計算誤差の問題を考えてみよう。
たとえば、3:4:5の直角三角形で、3*3+4*4 = 25 だが、sqrt(25)は実数で計算するから、 計算誤差で4.99999で求まったらどうなるだろうか?
1~100までの数値で、”int a = sqrt( (double)(i*i) ) ;” を計算してみて、 異なる値が求まることはあるか? 多少の計算誤差があっても正しく処理が行われるにはどうすればいいか、考えてみよう。
(2) 無駄な答えについて考えてみよう。
このプログラムの答えでは、簡単な整数比の答えの「整数倍の答え」も表示されてしまう。 たとえば、(3:4:5)の答えのほかに、(6:8:10)も表示される。 こういった答えを表示しないようにするにはどうすればよいか?
また、この2つのプログラムの処理時間を実際に比べてみる。
int main() {
time_t start , end ;
// time() 関数は、秒数しか求まらないので、
// あえて処理を1000回繰り返し、数秒かかる処理にする。
start = time( NULL ) ;
for( int i = 0 ; i < 1000 ; i++ ) {
// ただし、関数内のprintfをコメントアウトしておくこと
integer_triangle( 100 ) ;
}
end = time( NULL ) ;
printf( "%lf\n" , difftime( end , start ) ) ;
return 0 ;
}
再帰プログラミング
組み合わせ問題では、forループの多重の入れ子で問題を解けない場合が多い。 (書けないことはないけど無駄なループで処理が遅くなるか、入れ子段数が可変にできない。)
こういった場合には、再帰プログラミングがよく利用される。 もっとも簡単な再帰の例として、階乗のプログラムを考える。 通常であれば、以下のような for ループで記述することになるだろう。
// 階乗の計算
int fact( int x )
{ // ループ
int f = 1 ;
for( int i = 2 ; i <= x ; i++ )
f = f * i ;
return f ;
}
再帰呼び出しでは、関数の処理の中に、自分自身の関数呼び出しが含まれる。 また、無限に自分自身を呼び出したら処理が止まらないので、 問題を一つ小さくして、これ以上小さくできないときは処理を止めるように記述する。
int fact( int x )
{ // 再帰呼び出し
if ( x <= 1 )
return 1 ;
else
return x * fact( x - 1 ) ;
}
ここ以降は、指定長さを指定辺の組み合わせで作ると、Flood-fill の選択とする。
指定長を指定辺の組み合わせで作る
再帰を使った簡単なパズル問題として、以下のプログラムを作成したい。
配列の中に、複数の辺の長さが入っている。これを組み合わせて指定した長さを作れ。 使用する辺はできるだけ少ない方がよい。
int a[] = { 4 , 5 , 2 , 1 , 3 , 7 } ;
(例) 辺の長さ10を作るには、(5,4,1)とか(7,3)などが考えられる。
これは、ナップサック問題の基本問題で、容量の決まったナップサックに最大量入れる組合せを求めるのと同じである。
このプログラムを解くには…
10 を [4,5,2,1,3,7] で作るには... (0) 6=10-4 を [5,2,1,3,7]で作る。 (1) 5=10-5 を [4,2,1,3,7]で作る。 (2) 8=10-2 を [5,4,1,3,7]で作る。 (3) 9=10-1 を [5,2,4,3,7]で作る。 (4) 7=10-3 を [5,2,1,4,7]で作る。 (5) 3=10-7 を [5,2,1,3,4]で作る。
そこで、ここまでの考えを、以下のようなプログラムで記述してみる。
// 指定されたデータを入れ替える。
void swap( int*a , int*b )
{ int x = *a ;
*a = *b ;
*b = x ;
}
void check( int array[] , int size , int len , int n )
{
// array[] 配列
// size 配列サイズ
// len 作りたい長さ
// n 使った個数
for( int i = n ; i < size ; i++ ) {
// i番目を先頭に...
swap( &array[ n ] , &array[ i ] ) ;
printf( "check( array , %d , %d , %d )\n" ,
size , len - array[ n ] , n+1 ) ;
// 最初のswapでの変更を元に戻す。
swap( &array[ i ] , &array[ n ] ) ;
}
}
int main() {
int a[] = { 4 , 5 , 2 , 1 , 3 , 7 } ;
check( a , 6 , 10 , 0 ) ;
}
(1) これを再帰呼び出しにしてみよう。どう書けばいい?
void check( int array[] , int size , int len , int n )
{
// array[] 配列
// size 配列サイズ
// len 作りたい長さ
// n 使った個数
if ( len < 0 ) {
// 指定した丁度の長さを作れなかった。
;
} else if ( len == 0 ) {
// 指定した長さを作れたので答えを表示。
for( int i = 0 ; i < n ; i++ ) {
printf( "%d " , array[ i ] ) ;
}
printf( "\n" ) ;
} else {
// 問題を一つ小さくして再帰。
for( int i = n ; i < size ; i++ ) {
swap( &array[ n ] , &array[ i ] ) ;
printf( "check( array , %d , %d , %d )\n" ,
size , len - array[ n ] , n+1 ) ;
check( array , size , len - array[ n ] , n + 1 ) ;
swap( &array[ i ] , &array[ n ] ) ;
}
}
}
(2) 少ない組み合わせの方がポイントが高い場合には、プログラムをどう変更する?
(3) 答えが1つだけで良い場合は、プログラムをどう変更する?
(4) このプログラムでは、冗長な答えがあるか?ないか?検討せよ。
(5) 前設問の整数比直角三角形のプログラムで、冗長な答えを削除するプログラムを作成せよ。
# ただし、(2)〜(5)は、演習の実験の時間内でできる範囲とする。
Flood fill アルゴリズム
前の問題は、今年度のプログラミングコンテストの課題のパズルとは、方向性が違うので、今年度のプロコンの競技部門に近いパズルネタで演習。(Wikipedia Flood-fill参照)
以下の image のような2次元配列が与えられたら、指定座標(x,y)を中心に周囲を塗りつぶす処理を作成せよ。
include <stdio.h>
// *は壁 SPCは白 この領域の指定位置を#で塗りつぶす。
char image1[10][10] = { // (4,4)始点で塗りつぶし後
"*********" , // *********
"* * *" , // * *###*
"* * *" , // * *###*
"* * *" , // * *####*
"*** ***" , // ***###***
"* * *" , // *####* *
"* * *" , // *###* *
"* * *" , // *###* *
"*********" , // *********
} ;
char image2[10][10] = { // 応用問題用の画像例
"*********" , // * のような隙間は通り抜けられる
"* * *" , // * ようにするにはどうすればいい?
"* ** *" , // **
"* ** *" , // ** これは通り抜けられない
"*** ***" , // **
"* * *" ,
"* * *" ,
"* * *" ,
"*********" ,
} ;
// 盤面を表示
void print_image( char image[10][10] ) {
for( int y = 0 ; y < 9 ; y++ ) {
for( int x = 0 ; x < 9 ; x++ ) {
printf( "%c" , image[y][x] ) ;
}
printf( "\n" ) ;
}
}
// 再帰呼び出しを使った flud_fill アルゴリズム
void flood_fill( char image[10][10] , int x , int y , char fill ) {
// 指定座標が空白なら
if ( image[y][x] == ' ' ) {
// その座標を埋める
image[y][x] = fill ;
//////////////////////////////////////
// ここに周囲をflud_fillする処理を書く //
//////////////////////////////////////
}
}
int main() {
print_image( image1 ) ;
flood_fill( image1 , 4 , 4 , '#' ) ;
print_image( image1 ) ;
return 0 ;
}
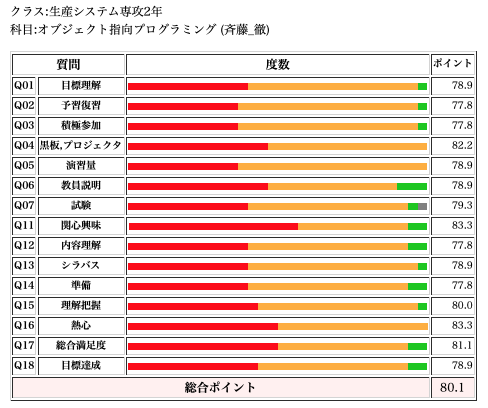
応用問題
Wikipediaのflood-fill のプログラムの説明のアルゴリズムでは、左図黒のような斜めに並んだブロックは、境界として通り抜けられないようにつくられている。
そこで、斜めに並んだブロックは通り抜けられるルールとした場合のプログラムを記述せよ。
プログラムと数値型
コンピュータの中では、2進数で値を表現するが、組み込み系のような小さいコンピュータでは、たくさんの桁を必要とする情報を扱うことが苦手である。そこで、C言語で数値を扱う型と、その型で扱える数値の範囲や問題点を説明する。
補足資料:プログラミングの基礎として、C言語の基礎を示す。
数値を扱う型
C言語では、データを覚える型を大きく2つに分けると、整数型(int)と実数型(float)に分けられる。
整数型(int)
整数型も正の値しか覚えられない符号無し型(unsigned int)と、符号付き型(signed int)に分けられる。さらに、その値を8bitで覚える文字型(char)、16bitで覚える short int型、32bitで覚える int 型、64bitで覚える long int 型(※C言語では long int で宣言すると32bitの場合も多いので要注意)がある。
| 精度 | 符号あり | 符号なし |
| 8bit | char | unsigned char |
| 16bit | short int | unsigned short int |
| 32bit | int | unsigned int |
| 64bit | long int※ | unsigned long int※ |
符号付きのデータは、負の数は2の補数によって保存する。この場合2進数の最上位bitは、負の数であれば必ず1となる。
整数型で扱える数
例えば、2進数3桁であれば、000,001,010,011,100,101,110,111 で、10進数であれば 0~7 の8通りの値が扱える。
(例) 符号なしの1byte(8bit)であれば、いくつの数を扱えるであろうか?
一般的に N bit であれば、0~(2N-1) までの値が扱える。
| bit数 | 型 | 符号なし | |
| 8 | unsigned char | 0~28-1 | 0~255 |
| 16 | unsigned short int | 0~216-1 | 0~65535 |
| 32 | unsigned int | 0~232-1 | 0~4294967295 |
符号付きであれば、2の補数表現で最上位bitが0であれば正の数、1であれば負の数を表す。このため、N bit の符号つき整数は、-2N-1から2N-1-1の範囲の値を覚えられる。
| bit数 | 型 | 符号あり | |
| 8 | char | -27~27-1 | -128~127 |
| 16 | short int | -215~215-1 | -32768~32767 |
| 32 | int | -231~231-1 | -2147483648~2147483647 |
数値の範囲の問題で動かないプログラム
この話だけだと、扱える数値の上限について実感がわかないかもしれないので、以下のプログラムをみてみよう。
組み込み系のコンピュータでは、int 型でも、一度に計算できるbit数が少ない。例えば、int型が16bitコンピュータでは、以下のプログラムは期待した値が計算できない。以下の例では、16bit int型として short int で示す。
// コード1
#include <stdio.h>
#include <math.h>
int main() { // 原点から座標(x,y)までの距離を求める
short int x = 200 ;
short int y = 200 ;
short int r2 = x*x + y*y ; // (x,y)までの距離の2乗
short int r = sqrt( r2 ) ; // sqrt() 平方根
printf( "%d\n" , r ) ; // 何が求まるか?
return 0 ; // (例) 282ではなく、120が表示された。
}
コンピュータで一定時間かかる処理を考えてみる。
// コード2.1 // 1 [msec] かかる処理が以下のように書いてあったとする。 short int i ; for( i = 0 ; i < 1000 ; i++ ) NOP() ; // NOP() = 約1μsecかかる処理とする。 // コード2.2 // 0.5 [sec]かかる処理を以下のようにかいた。 short int i ; for( i = 0 ; i < 500000 ; i++ ) NOP() ; // でもこの処理は16bitコンピュータでは、1μsecもかからずに終了する。なぜか?
上記の例は、性能の低い16bit コンピュータの問題で、最近は32bit 整数型のコンピュータが普通だし、特に問題ないと思うかもしれない。でも、32bit でも扱える数の範囲で動かなくなるプログラムを示す。
OS(unix) では、1970年1月1日からの経過秒数で時間を扱う。ここで、以下のプログラムは、正しい値が計算できない有名な例である。(2004年1月11日にATMが動かなくなるトラブルの原因だった)
// コード3.1 int t1 = 1554735600 ; // 2019年4月09日,00:00 int t2 = 1555340400 ; // 2019年4月16日,00:00 // この2日の真ん中の日を求める。 // 以下のプログラムは、正しい 2019年4月12日12:00 が求まらない。なぜか? int t_mid = (t1 + t2) / 2; // (例) 1951年03月25日 08:45 になった。 // コード3.2 // 以下のプログラムは正しく動く。 // time_t 型(時間処理用の64bit整数) time_t t1 = 1554735600 ; // 2019年4月09日,00:00 time_t t2 = 1555340400 ; // 2019年4月16日,00:00 // たとえ32bitでも溢れない式 time_t t_mid = t1 + (t2 - t1) / 2 ;
コンピュータと2進数
3年の情報制御基礎の授業の一回目。この授業では、情報系以外の学生も受講する。昨年度は、プログラムも作る話から、プログラムの基礎の話もしたけど、他学科からの学生さんには難しい所もあったので、共通的な話題を増やす予定。
出席確認は、右側のQRコードを撮影するか、QRコードをクリックして、Microsoft Forms で出席を報告してください。
もし、Office365にLoginできない場合は、直接出席を伝えて下さい。
情報制御基礎のシラバス
情報制御基礎では、ここに上げたシラバスに沿って授業を行う。
基本的に、センサーから読み取ったデータを使って動くシステムを作る場合の、知識ということでアナログ量・デジタル量の話から、移動平均やデータ差分といった数値処理や、そこで求まった値を制御に用いるための基礎的な話を行う。
コンピュータと組み込み系
最近では、コンピュータといっても様々な所で使われている。(1)科学技術計算用の大型コンピュータやインターネットの処理を行うサーバ群、(2)デスクトップパソコン、(3)タブレットPCやスマートフォンのような端末、(4)電化製品の中に収まるようなワンチップコンピュータなどがある。

ワンチップコンピュータ
身近で使われている情報制御という点では、(4)のような小型のコンピュータも多く、こういったものは組み込み型コンピュータとも呼ばれる。しかし、こういったコンピュータは、小さく機能も限られているので、
- 組み込み系では、扱える数値が8bit や 16bit といった精度しかなかったり、
- 複雑な計算をするには、処理時間がかかったりする
ため、注意が必要である。
この情報制御基礎の授業では、組み込み系のコンピュータでも数値を正しく扱うための知識や、こういった小さいコンピュータで制御を行うことを踏まえた知識を中心に説明を行う。
2進数と10進数
コンピュータの中では、電圧が高い/低いといった状態で0と1の2通りの状態を表し、その0/1を組み合わせて、大きな数字を表す(2進数)。
練習として、2進数を10進数で表したり、10進数を2進数に直してみよう。
N進数を10進数に変換
N進数で “abcde” があったとする。(2進数で”10101″とか、10進数で”12345″とか)
この値は、を意味する。
(例1)
(例2)
10進数をN進数に変換
N進数のは、
であることから、値をNで割った余りを求めると、N進数の最下位桁eを取り出せる。
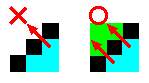
このため、10進数で与えられた35を2進数に変換するのであれば、35を2で次々と割った余りを、下の桁から書きならべれば2進数100011)2が得られる。
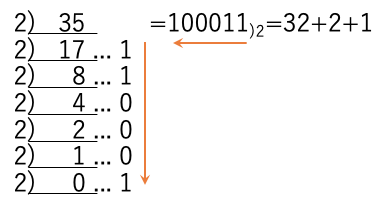
実数の場合
途中に小数点を含むN進数のab.cde)Nであれば、を意味する。ここで、小数点以下だけを取り出した、0.cde)Nを考えると、
の値に、Nをかけると、
となる。よって、小数部にNをかけると、整数部分に小数点以下1桁目が取り出せる。
このため、10進数で与えられた、0.625を2進数に変換するのであれば、0.625に次々と2をかけて、その整数部を上の桁から書きならべれば、2進数0.101)2が得られる。
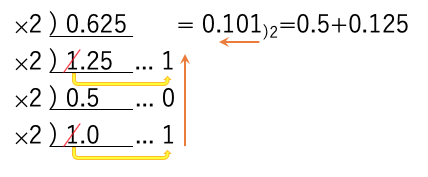
ただし、10進数で0.1という値で、上記の計算を行うと、延々と繰り返しが発生する。つまり、無限小数になるので注意せよ。
2の補数と負の数
コンピュータの中で引き算を行う場合には、2の補数がよく使われる。2の補数とは、2進数の0と1を入替えた結果(1の補数)に、1を加えた数である。

元の数に2の補数
を加えると(2進数が8bitの数であれば)、どのような数でも1,0000,0000という値になる。この先頭の9bit目が必ずはみ出し、この値を覚えないのであれば、元の数+2の補数=0とみなすことができる。このことから、2の補数= (-元の数) であり、負の数を扱うのに都合が良い。
練習問題
(1) 自分の誕生日で、整数部を誕生日の日、小数点以下を誕生日の月とした値について、2進数に変換せよ。(例えば、2月7日の場合は、”7.02″という小数点を含む10進数とする。)
変換の際には、上の説明の中にあるような計算手順を示し、その2進数が元の値を表していることを確認すること。
小数点以下は、最大7桁まで求めれば良い。
(2) 自分の誕生日の日と、自分の学籍番号の下2桁の値を加えた値について、8bitの2進数で表わせ。(2月7日生まれの出席番号13番なら7+13=21)
その後、8bitの2進数として、2の補数を求めよ。
構造体でオブジェクト指向の最初の一歩
構造体でオブジェクト指向もどき
例えば、名前と年齢の構造体で処理を記述する場合、 以下の様な記載を行うことで、データ設計者とデータ利用者で分けて 仕事ができることを説明。
// この部分はデータ構造の設計者が書く
// データ構造を記述
struct Person {
char name[10] ;
int age ;
} ;
// データに対する処理を記述
void setPerson( struct Person* p , char s[] , int a ) {
// ポインタの参照で表記
strcpy( (*p).name , s ) ;
(*p).age = a ;
}
void printPerson( struct Person* p ) {
// アロー演算子で表記 "(*p).name" は "p->name" で書ける
printf( "%s %d¥n" ,
p->name , p->age ) ;
}
// この部分は、データ利用者が書く
int main() {
// Personの中身を知らなくてもいいから配列を定義(データ隠蔽)
struct Person saitoh ;
setPerson( &saitoh , "saitoh" , 55 ) ;
struct Person table[ 10 ] ; // 初期化は記述を省略
for( int i = 0 ; i < 10 ; i++ ) {
// 出力する...という雰囲気で書ける(手続き隠蔽)
printPerson( &table[i] ) ;
}
return 0 ;
}
このプログラムの書き方では、mainの中を読むだけもで、 データ初期化とデータ出力を行うことはある程度理解できる。 この時、データ構造の中身を知らなくてもプログラムが理解でき、 データ実装者はプログラムを記述できる。これをデータ構造の隠蔽化という。 一方、setPerson()や、printPerson()という関数の中身についても、 初期化・出力の方法をどうするのか知らなくても、 関数名から動作は推測できプログラムも書ける。 これを手続きの隠蔽化という。
C++のクラスで表現
上記のプログラムをそのままC++に書き直すと以下のようになる。
#include <stdio.h>
#include <string.h>
// この部分はクラス設計者が書く
class Person {
private: // クラス外からアクセスできない部分
// データ構造を記述
char name[10] ; // メンバーの宣言
int age ;
public: // クラス外から使える部分
// データに対する処理を記述
void set( char s[] , int a ) { // メソッドの宣言
// pのように対象のオブジェクトを明記する必要はない。
strcpy( name , s ) ;
age = a ;
}
void print() {
printf( "%s %d¥n" , name , age ) ;
}
} ; // ← 注意ここのセミコロンを書き忘れないこと。
// この部分はクラス利用者が書く
int main() {
Person saitoh ;
saitoh.set( "saitoh" , 55 ) ;
saitoh.print() ;
// 文法エラーの例
printf( "%d¥n" , saitoh.age ) ; // phoneはprivateなので参照できない。
return 0 ;
}
用語の解説:C++のプログラムでは、データ構造とデータの処理を、並行しながら記述する。 データ構造に対する処理は、メソッド(method)と呼ばれる。 データ構造とメソッドを同時に記載したものは、クラス(class)と呼ぶ。 そのclassに対し、具体的な値や記憶域が割り当てられたものをオブジェクト(object)と呼ぶ。
引数渡しについて
オブジェクト指向の授業では他学科出身の人も多いので、引数渡しの理解が浅いことから、別途説明を行う。
値渡し、ポインタ渡し、参照渡し
構造体の使い方の話では、関数との構造体のデータ渡しでポインタなどが出てくるので、 値渡し・ポインタ渡し・参照渡しの説明。(参照渡しはC++で導入された考え方)
値渡し
C言語の基本は、値渡し。呼び出し側の実引数は、関数側の仮引数に値がコピーされる。 このため、呼び出し側の変数(下の例ではa)の中身は変化しない。 よって、関数の呼び出しで呼び出し側の変数が勝手に中身が変わらないので、予想外の変数の中身の変化が無く分かりやすい。
// 値渡し(call by value)の例
void foo( int x ) {
x++ ;
printf( "%d¥n" , x ) ;
}
void main() {
int a = 123 ;
foo( a ) ; // 124が表示
foo( a ) ; // 124が表示
}
ポインタ渡し
しかし、上の例では、foo()の呼び出しで、変数aの中身が変化してくれたほうが都合が良い場合もある。 この場合は、C言語ではポインタを使って記述する。 このように、関数を呼び出して、手元の変数が変化することは、副作用と呼ばれる。 副作用の多いプログラムは、変数の値の管理がわかりにくくなるので、副作用は最小限に記述すべき。
// ポインタ渡し(call by pointer)の例
void foo( int *px ) {
(*px)++ ;
printf( "%d¥n" , (*px) ) ;
}
void main() {
int a = 123 ;
foo( &a ) ; // 124が表示
foo( &a ) ; // 125が表示
}
参照渡し
しかし、ポインタを多用すると、ポインタを動かしてトラブルも増えることから、ポインタはあまり使わない方が良い。 そこで、C++では参照型というものがでてきた。
// 参照型(call by reference)の場合
void foo( int &x ) {
x++ ;
printf( "%d¥n" , x ) ;
}
void main() {
int a = 123 ;
foo( a ) ; // 124が表示
foo( a ) ; // 125が表示
}
参照型は、ポインタを使っていないように見えるけれども、機械語レベルでみればポインタ渡しの命令を自動的に生成してくれるだけ。
処理時間のオーダー(回答編)
2分探索法の処理時間の見積もり
コンピュータで2分探索法で、データ100件で10[μsec]かかったとする。
データ10000件なら何[sec]かかるか?
解答
2分探索法なので、処理時間はO(logN) であり、T(N) = Tα+Tβ✕N で表される。
T(100) =10μsec = Tβ✕ log 100
となる。ここで、logの底は、底変換の公式を使うと、底の違いはTβ に含めて考えればいいので、今回は10を底にして考える。
10μsec = Tβ ✕ log10100=Tβ✕2
Tβ=5μsec
よって、
T(10000) = 5μsec✕log1010000=20μsec
処理時間の式をオーダ表記
の処理時間を要するアルゴリズムを、オーダー記法で書くとどうなるか?
解答
ここで問題となるのは、 と
の値が、Nが巨大な値の時にどっちが大きいかが問題となる。
そこで、それぞれの値を分子分母にして N→∞で、∞に拡散するか、0に収束するかを判定すればいい。
ここで、ロピタルの定理より、分子分母をそれぞれ微分すると、
よって、分子の方が巨大な値になるので、この処理時間は、
で表せる。
ループ処理時間とオーダー記法と再帰
先週に、単純繰り返し処理の時間分析をやったので、次のステップに。
2分探索法の処理時間
データを探す処理において、単純検索より速い方法ということで、2分探索法の処理速度見積もりを行う。
// 2分探索法 O(log N)
int a[ 1000 ] = { 対象となるデータ } ;
int size = N ; // データ数 N
int L = 0 ; // L=下限のデータの場所
int R = size ; // R=上限のデータ+1の場所
while( L != R ) {
int M = (L + R) / 2 ; // 計算は整数型で行われることに注意
if ( a[M] == key ) // 見つかった
break ;
else if ( a[M] < key ) // |L |M. |R
L = M + 1 ; // |----------|-+---------|
else // |L---------|M|
R = M ; // |M+1------|R
}
上記のようなプログラムの場合、処理に要する時T(N)は、
処理は、対象となるデータ件数が繰り返し毎に半分となり、対象データ件数が1件になれば処理が終わる。このことから、
となることから、 の関係が成り立つ。よって、
は、以下のように表せる。
単純なソート(最大選択法)の処理時間
次に、並べ替え処理の処理時間について考える。
int a[ 1000 ] = { 対象となるデータ } ;
int size = N ;
for( int i = 0 ; i < size - 1 ; i++ ) {
int tmp ;
// i..size-1 の範囲で一番大きいデータの場所を探す
int m = i ;
for( int j = i + 1 ; j < size ; j++ ) {
if ( a[j] > a[m] )
m = j ;
}
// 一番大きいデータを先頭に移動
tmp = a[i] ;
a[i] = a[m] ;
a[m] = tmp ;
}
このプログラムの処理時間T(N)は… (参考 数列の和の公式)
となる。
オーダー記法
ここまでのアルゴリズムをまとめると、処理時間に大きく影響する部分は、最後の項の部分であり、特にその項の係数は、コンピュータの処理性能に影響を受けるが、アルゴリズムの優劣を考える場合は、それぞれ、
の部分の方が重要である。
| 単純サーチ | |
| 2分探索法 | |
| 最大選択法 |
そこで、アルゴリズムの優劣を議論する場合は、この処理時間の見積もりに最も影響する項で、コンピュータの性能によって決まる係数を除いた部分を抽出した式で表現する。これをオーダー記法と言う。
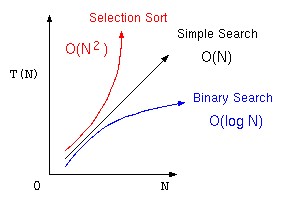
| 単純サーチ | オーダーNのアルゴリズム | |
| 2分探索法 | オーダー log N のアルゴリズム | |
| 最大選択法 | オーダー N2 のアルゴリズム |
練習問題
- コンピュータで2分探索法で、データ100件で10[μsec]かかったとする。
データ10000件なら何[sec]かかるか?
(ヒント: 底変換の公式) の処理時間を要するアルゴリズムを、オーダー記法で書くとどうなるか?また、このようなアルゴリズムの例を答えよ。
の処理時間を要するアルゴリズムを、オーダー記法で書くとどうなるか?
(ヒント: ロピタルの定理)
再帰呼び出しの予習
若干、時間が余ったので、再帰呼出しと簡単な処理の例を説明する。
最初に定番の階乗(fact)

次に、フィボナッチ数列の場合

