リスト構造の利点は、データを扱う件数が可変にできる所。 通常なら配列で書いていたプログラムも、リストを使うと便利。 以下のようにデータの途中にデータを挿入する場合でも、 記入場所を確保するためのデータの移動 の処理が不要で、 単純なリストのつなぎかえの の処理で済む。

// あえてcons()を使わずに書いておく
void insert_next( int x , struct List* p ) {
struct List* ans ;
ans = (struct List*)malloc( sizeof( struct List ) ) ;
if ( ans != NULL ) {
ans->data = x ;
ans->next = p->next ;
p->next = ans ;
}
}

Stack(スタック)

データの後入れ先出し(Last In First Out)を行う Stack は基本的なデータの管理法。 配列で実装すれば、以下のような処理となる。

int stack[ SIZE ] ;
int sp = 0 ;
void push( int x ) {
stack[ sp++ ] = x ;
}
int pop() {
return stack[ --sp ] ;
}
void main() {
push( 1 ) ; push( 2 ) ; push( 3 ) ;
printf( "%d" , pop() ) ;  // 3
printf( "%d" , pop() ) ;  // 2
printf( "%d" , pop() ) ;  // 1
}

しかし配列であれば、SIZEを超えるデータは保管できない。そこで、push/pop をリスト構造で 記載してみる。

struct List* stack = NULL ;
void push( int x ) {
stack = cons( x , stack ) ;
}
int pop() {
int ans = stack->data ;
struct List* del = stack ;
stack = stack->next ;
free( del ) ;
return ans ;
}

Queue(待ち行列)

先入れ先出し(First In First Out)は、一般的に待ち行列と呼ばれ、 プログラムは、先頭データと末尾データの2つの情報で管理される。

int queue[ SIZE ] ;
int wp = 0 , int rp = 0 ;
void put( int x ) {
queue[ wp++ ] = x ;         // リングバッファ法
if ( wp >= SIZE ) wp = 0 ;  // 末尾なら先頭に戻る
}
int get() {
int ans = queue[ rp++ ] ;
if ( rp >= SIZE ) rp = 0 ;  // 末尾なら先頭に戻る
return ans ;
}
void main() {
put( 1 ) ; put( 2 ) ; put( 3 ) ;
printf( "%d" , get() ) ;  // 1
printf( "%d" , get() ) ;  // 2
printf( "%d" , get() ) ;  // 3
}

ただし、上記プログラムは登録件数が0になったことのチェックが無い手抜き記載なので、 理解できている人はさらに対策を記載する必要があることを考えること。

この待ち行列をリストを使ってプログラムで書けば、以下のようになる。 ただし、このリストのつなぎかえでは、データ件数0の状態が問題になるため、 最初にdummyデータが1件入れてあるものとする。

struct List* top = cons( 999 , NULL ) ; // dummy
struct List** tail = &( top->next ) ;
void put( int x ) {
*tail = cons( x , NULL ) ;
tail = &( (*tail)->next ) ;
}
int get() {
int ans = top->data ;
struct List* del = top ;
top = top->next ;
free( del ) ;
return ans ;
}

# 先週の講義のメモが残してないので、１週遅れで記載。

前回の説明では、リストを処理で手作業で作っていたが、 データの入力に合わせて追加して区処理を説明する。

先頭挿入型の追加処理

配列でデータを扱えば、C言語では固定サイズになるため、リスト構造を使えば不定長の データの取り扱いも楽。

struct List {
int data ;
struct List* next ;
} ;
struct List* cons( int x , struct List* n ) {
struct List* ans ;
if ( (ans = (struct List*)malloc( sizeof(struct List ))) != NULL ) {
ans->data = x ;
ans->next = n ;
}
return ans ;
}
void main() {
struct List* top = NULL ;
int  x ;
while( scanf( "%d" , &x ) == 1 ) {
top = cons( x , top ) ;
}
}

このプログラムでは、リストの先頭に次々とデータを挿入していく。 このためデータは、挿入順と逆に並ぶことになる。

末尾追加型の追加処理

前の例では、管理するためのポインタがtopだけで良いため、シンプルではあるが、 データが逆順になってしまう。データの挿入順に並びたいのであれば、以下のような プログラムとなる。

void main() {
struct List* top = NULL ;
struct List** tail = &top ;
int  x ;
while( scanf( "%d" , &x ) == 1 ) {
*tail = cons( x , NULL ) ;
tail = &( (*tail)->next ) ;
}
}

しかしこのプログラムでは、tail の宣言が『Listへのポインタのポインタ』といった宣言で、 必ずしも読みやすいものではない。しかし、式の部分的な型が何なのかを明確に 理解できれば、イメージ図があれば、それなりに理解もできるようになるはず。

// ややこしい部分の型を考える。
&( (*tail)->next ) の型は？
tail               : List**
*tail              : List*  (List**の先を参照)
(*tail)->next      : List*  (List*の先のnext部を参照)
&( (*tail)->next ) : List** (next部のアドレスを取り出す)

先週のUMLの全体像の説明を受け、今日はデータ構造の説明のための図ということで、 構造図について説明する。

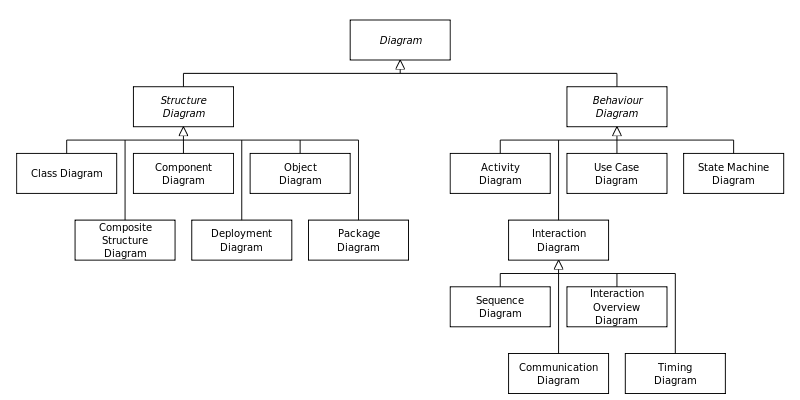
まずは、基本のクラス図について説明し、 可視性：public(+),private(-),protected(#)を、要素やメソッドにつけてあらわす。 継承がある場合には、派生側から基底クラスに白抜き三角矢印"―▹"で結ぶ。 クラス間の関係は、関連(assosiation)といい、直線で結ぶ。 直線の上には関連の説明をする意味を書き添え、両端には役割(ロール)を記載する。 直線の下には、多重度などを書き添える。

クラス間に包含関係がある場合には、全体と部分という関係があり、集約と呼ぶ。 この集約のうち、特に結びつきが強いものは合成(コンポジション)と呼ぶ。 単なる集約は、部品が単独でも存在しうる場合に使われ、"―◇"で接続する。 一方、コンポジションは親クラスと共に消滅するような強い結びつきであり、 UML記号としては"―◆"で接続する。

クラス図を具体的なデータを交えて記載するものは、オブジェクト図と呼ばれ、 設計開始時に関係者にヒアリングしながら書いたり、クラス設計が進む中で、 設計を検証するために具体的なインスタンスを書き込んで使う。

パッケージ図は、複数のクラスからなるものの全体的なグルーピングして記述するもので、 グループ化されたものをフォルダアイコンでまとめて、その間の関連を記載する。

コンポーネント図は、複数のクラスで構成される処理で、１つ以上のインタフェースを用意し、 あたかも１つのクラスのように取り扱って表現する図。 提供側インタフェース"―○"と、要求側インタフェース"―⊂"で結びつきを表現する。

(図は、Wikipediaなどからの引用)