配列やリスト構造のデータの中から、目的となるデータを探す場合、配列であれば2分探索法が用いられる。これにより、配列の中からデータを探す処理は、O(log N)となる。(ただし事前にデータが昇順に並んでいる必要あり)

// 2分探索法
import java.util.*;

public class Main {
    public static int bin_search( int[] a , int key , int L , int R ) {
        // Lは探す範囲の左端
        // Rは探す範囲の右端+1(注意!!)
        while( R > L ) {
            int m = (L + R) / 2 ;
            if ( a[m] == key )
                return m ;
            else if ( a[m] > key )
                R = m ;
            else
                L = m + 1 ;
        }
        return -1 ;
    }
    public static void main(String[] args) throws Exception {
        int[] array = {
            11, 13, 27, 38, 42, 64, 72, 81
        } ;
        System.out.println( bin_search( array , 64 , 0 , array.length ) ) ;
        System.out.println( bin_search( array , 14 , 0 , array.length ) ) ;
    }
}

• Javaによる2分探索法

// 2分探索法
int array[ 8 ] = { 11, 13 , 27, 38, 42, 64, 72 , 81 } ;

int bin_search( int a[] , int key , int L , int R ) {
   // Lは、範囲の左端
   // Rは、範囲の右端+1 (注意!!)
   while( R > L ) {
      int m = (L + R) / 2 ;
      if ( a[m] == key )
         return m ;
      else if ( a[m] > key )
         R = m ;
      else
         L = m + 1 ;
   }
   return -1 ; // 見つからなかった
}

void main() {
   printf( "%d¥n" , bin_search( array , 0 , 8 ) ) ;
}

一方、リスト構造ではデータ列の真ん中のデータを取り出すには、先頭からアクセスするしかないのでO(N)の処理時間がかかり、極めて効率が悪い。リスト構造のようにデータの追加が簡単な特徴をもったまま、もっとデータを高速に探すことはできないものか？

2分探索木

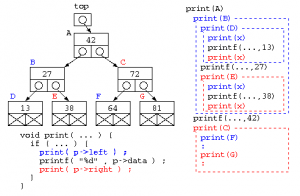
ここで、データを探すための効率の良い方法として、2分探索木(2分木)がある。以下の木のデータでは、分離する部分に1つのデータと、左の枝(下図赤)と右の枝(下図青)がある。

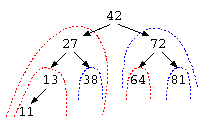
この枝の特徴は何だろうか？この枝では、中央のデータ例えば42の左の枝には、42未満の数字の枝葉が繋がっている。同じように、右の枝には、42より大きな数字の枝葉が繋がっている。この構造であれば、64を探したいなら、42より大きい→右の枝、72より小さい→左の枝、64が見つかった…と、いう風にデータを探すことができる。

特徴としては、1回の比較毎にデータ件数は、(N-1)/2件に減っていく。よって、この方法であれば、O(log N)での検索が可能となる。これを2分探索木とよぶ。

このデータ構造をプログラムで書いてみよう。

import java.util.*;

class BTreeNode {
    int       data ;
    BTreeNode left ;
    BTreeNode right ;
    
    BTreeNode( int x , BTreeNode l , BTreeNode r ) {
        this.data  = x ;
        this.left  = l ;
        this.right = r ;
    }
}

public class Main {
    public static void print_tree( BTreeNode p ) {
        if ( p != null ) {
            print_tree( p.left ) ;
            System.out.print( p.data + " " ) ;
            print_tree( p.right ) ;
        }
    }
    public static int tree_search( BTreeNode p , int key ) {
        while( p != null ) {
            System.out.println( "p.data=" + p.data + " : key=" + key ) ;
            if ( p.data == key )
                return key ;
            else if ( p.data > key )
                p = p.left ;
            else
                p = p.right ;
        }
        return -1 ;
    }
    public static void main(String[] args) throws Exception {
        BTreeNode top =
            new BTreeNode( 42 ,
                           new BTreeNode( 27 ,
                                          new BTreeNode( 13 , null , null ) ,
                                          new BTreeNode( 38 , null , null ) ) ,
                           new BTreeNode( 72 ,
                                          new BTreeNode( 64 , null , null ) ,
                                          new BTreeNode( 81 , null , null ) ) ) ;
        print_tree( top ) ;
        System.out.println() ;
        if ( tree_search( top , 64 ) >= 0 )
            System.out.println( "Find." ) ;
    }
}

• 2分探索木

struct Tree {
   struct Tree* left ;
   int          data ;
   struct Tree* right ;
} ;

// 2分木を作る補助関数
struct Tree* tcons( struct Tree* L ,
                    int          d ,
                    struct Tree* R ) {
   struct Tree* n = (struct Tree*)malloc(
                       sizeof( struct Tree ) ) ;
   if ( n != NULL ) { /* (A) */
      n->left = L ;
      n->data = d ;
      n->right = R ;
   }
   return n ;
}

// 2分探索木よりデータを探す
int tree_search( struct List* p , int key ) {
   while( p != NULL ) {
      if ( p->data == key )
         return key ;
      else if ( p->data > key )
         p = p->left ;
      else
         p = p->right ;
   }
   return -1 ; // 見つからなかった
}
struct Tree* top = NULL ;

void main() {
   // 木構造をtcons()を使って直接生成 (B)
   top = tcons( tcons( tcons( NULL , 13 , NULL ) ,
                       27 ,
                       tcons( NULL , 38 , NULL ) ) ,
                42 ,
                tcons( tcons( NULL , 64 , NULL ) ,
                       72 ,
                       tcons( NULL , 81 , NULL ) ) ) ;
   printf( "%d¥n" , tree_search( top , 64 ) ) ;
}

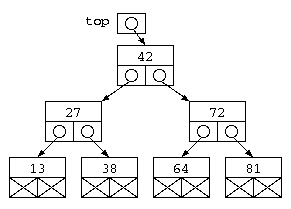
この方式の注目すべき点は、struct Tree {…} で宣言しているデータ構造は、2つのポインタと1つのデータを持つという点では、双方向リストとまるっきり同じである。データ構造の特徴の使い方が違うだけである。

理解度確認

• main() の (B) の部分 “top = tcons(…)” において、末端部に NULL を入れる理由を答えよ。

2分木に対する処理

2分探索木に対する簡単な処理を記述してみよう。

// (略)
public class Main {
    public static void print_tree( BTreeNode p ) {
        if ( p != null ) {
            print_tree( p.left ) ;
            System.out.print( p.data + " " ) ;
            print_tree( p.right ) ;
        }
    }
    public static int count( BTreeNode p ) { // データ件数を数える
        // 考えてみよう
    }
    public static int sum( BTreeNode p ) {   // 合計を求める
        // 考えてみよう
    }
    public static int max( BTreeNode p ) {   // 最大値を探す
         // 考えてみよう
    }
    public static void main(String[] args) throws Exception {
        BTreeNode top = /*(略)*/ ;
        print_tree( top ) ;
        System.out.println() ;
        System.out.println( count( top ) ) ; // データ件数を数える
        System.out.println( sum( top ) ) ;   // 合計を求める
        System.out.println( max( top ) ) ;   // 最大値を探す
    }
}

下記のC言語のプログラムをヒントとしておく。

// データを探す
int search( struct Tree* p , int key ) {
   // 見つかったらその値、見つからないと-1
   while( p != NULL ) {
      if ( p->data == key )
         return key ;
      else if ( p->data > key )
         p = p->left ;
      else
         p = p->right ;
   }
   return -1 ;
}
// データを全表示
void print( struct Tree* p ) {
   if ( p != NULL ) {
      print( p->left ) ;
      printf( "%d¥n" , p->data ) ;
      print( p->right ) ;
   }
}
// データ件数を求める
int count( struct Tree* p ) {
   if ( p == NULL )
      return 0 ;
   else
      return 1
             + count( p->left )
             + count( p->right ) ;
}
// データの合計を求める
int sum( struct Tree* p ) {
   if ( p == NULL )
      return 0 ;
   else
      return p->data
             + count( p->left )
             + count( p->right ) ;
}
// データの最大値
int max( struct Tree* p ) {
   while( p->right != NULL )
      p = p->right ;
   return p->data ;
}

これらの関数では、木構造の全てに対する処理を実行する場合には、再帰呼び出しが必要となる。