ハノイの塔
 ここまでは、簡単な再帰呼び出しのプログラムを例にして再帰方程式などの説明を行った。次に「ハノイの塔」の処理時間を例題に、プログラムの処理時間について分析を行う。
ここまでは、簡単な再帰呼び出しのプログラムを例にして再帰方程式などの説明を行った。次に「ハノイの塔」の処理時間を例題に、プログラムの処理時間について分析を行う。
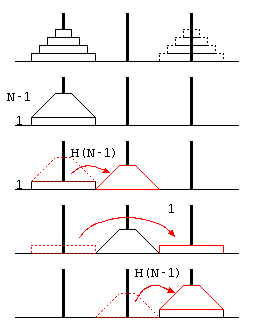
ハノイの塔は、3本の塔にN枚のディスクを積み、(1)1回の移動ではディスクを1枚しか動かせない、(2)ディスクの上により大きいディスクを積まない…という条件で、山積みのディスクを目的の山に移動させるパズル。
一般解の予想
ハノイの塔の移動回数を とした場合、 少ない枚数での回数の考察から、 以下の一般式で表せることが予想できる。
… ①
この予想が常に正しいことを証明するために、ハノイの塔の処理を、 最も下のディスク1枚への操作と、その上の(N-1)枚のディスクへの操作に分けて考える。
再帰方程式
上記右の図より、N枚の移動をするためには、上に重なるN-1枚を移動させる必要があるので、
… ②
… ③
ということが言える。(これがハノイの塔の移動回数の再帰方程式)
ディスクが枚の時、予想①が正しいのは明らか①,②。
ディスクが 枚で、予想が正しいと仮定すると、
枚では、
… ③より
… ①を代入
… ①の
の場合
となり、 枚でも、予想が正しいことが証明された。 よって数学的帰納法により、1枚以上で予想が常に成り立つことが証明できた。
これらのことから、ハノイの塔の処理時間は、で表せる。
再帰を用いた並び替え
データを並び替えるプログラムとして、繰り返し処理の分析では「選択法」について説明した。
選択法は、 のアルゴリズムで、あまり速い並び替え手法ではない。
| アルゴリズム | 処理時間のオーダー | ||
|---|---|---|---|
| バブルソート | |||
| 選択ソート | |||
| クイックソート, マージソート |
ここで、最も高速なアルゴリズムとしては、クイックソートが有名である。クイックソートプログラムは、処理時間のオーダはで表せる。
本当であれば、クイックソートのプログラムの処理時間の分析を説明したいけど、イメージがわかりにくいので、同じオーダ式であらわせるマージソートで説明を行う。
(マージソートのオーダは、クイックソートと同じだけど、計算途中のデータを一時的に覚える場所を確保する処理が必要で、その処理に手間がかかるため、効率はクイックソートに比べ遅くなる。)
import java.util.*;
// マージソートは、リスト構造を使っているので、
// クイックソートより効率が悪い。
// でもオーダーとしては、O( N log N ) のアルゴリズム
public class Main {
public static LinkedList merge_sort( LinkedList list ) {
// データ件数が1件ならソート不要
if ( list.size() <= 1 ) {
return list;
}
// 左右2つに分割
int mid = list.size() / 2 ;
LinkedList<Integer> left = new LinkedList<>( list.subList( 0 , mid ) ) ;
LinkedList<Integer> right = new LinkedList<>( list.subList( mid , list.size() ) ) ;
// 左右をそれぞれマージソート
LinkedList<Integer> sorted_left = merge_sort( left ) ;
LinkedList<Integer> sorted_right = merge_sort( right ) ;
// 左右のリストをマージする。
LinkedList merged = new LinkedList<>() ; // 初期状態は空っぽ
// 左右のリストの小さい方を取り出して答えに追加していく
while( !sorted_left.isEmpty() && !sorted_right.isEmpty() ) {
int left_top = sorted_left.get( 0 ) ;
int right_top = sorted_right.get( 0 ) ;
if ( left_top > right_top ) {
merged.add( sorted_right.removeFirst() ) ;
} else {
merged.add( sorted_left.removeFirst() ) ;
}
}
// 残ったリストを追加
while( !sorted_left.isEmpty() )
merged.add( sorted_left.removeFirst() ) ;
while( !sorted_right.isEmpty() )
merged.add( sorted_right.removeFirst() ) ;
return merged ;
}
public static void main( String[] args ) {
// ソート対象のデータ
LinkedList<Integer> data = new LinkedList<>() ;
data.add( 38 ) ;
data.add( 27 ) ;
data.add( 43 ) ;
data.add( 3 ) ;
data.add( 9 ) ;
data.add( 82 ) ;
data.add( 10 ) ;
System.out.println( "ソート前: " + data ) ;
LinkedList<Integer> sorted_data = merge_sort( data ) ;
System.out.println( "ソート後: " + sorted_data ) ;
}
}
- LinkedListを用いたマージソート(Paiza.io)
マージソートの分析
マージソートは、与えられたデータを2分割し、 その2つの山をそれぞれマージソートを行う。 この結果の2つの山の頂上から、大きい方を取り出す…という処理を繰り返すことで、 ソートを行う。
このことから、再帰方程式は、以下のようになる。
この再帰方程式を、N=1,2,4,8…と代入を繰り返していくと、 最終的に処理時間のオーダが、 となる。
:
よって、
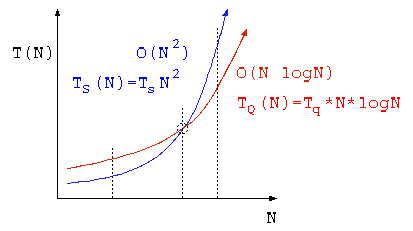
選択法とクイックソートの処理時間の比較
データ数 N = 10 件でソート処理の時間を計測したら、選択法で 10msec 、クイックソートで 20msec であった。
- データ件数 N= 100 件では、選択法,クイックソートは、それぞれどの程度の時間がかかるか答えよ。
- データ件数何件以上なら、クイックソートの方が高速になるか答えよ。
設問2 は、通常の関数電卓では求まらないので、数値的に方程式を解く機能を持った電卓が必要。