深さ優先探索(前順)
以前紹介した2分木の表示では、再帰呼び出しで木の処理を記述していた。
しかし、スタックを使って未処理のノードを保存しながらノードに対する処理を行えば、ループ処理で「すべての木のノード」に対する処理を記述できる。このような木に対する処理は、末端方向に処理が進むことが優先されるため深さ優先探索と呼ぶ。
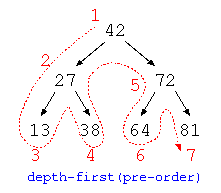
以下のプログラムで示す深さ優先探索では、ノードに対する処理を行ってから左の枝葉の処理が行われる。このような深さ優先探索は前順(pre-order)と呼ぶ。
このような探索は、ゲームですべての戦略の先読みを行う処理で用いられる。
import java.util.*;
class BTreeNode {
int data ;
BTreeNode left ;
BTreeNode right ;
BTreeNode( int x , BTreeNode l , BTreeNode r ) {
this.data = x ;
this.left = l ;
this.right = r ;
}
}
public class Main {
// 再帰呼び出しによる木の操作 = 深さ優先探索(前順)
public static void print_rec_depth_first_pre_order( BTreeNode p ) {
if ( p != null ) {
System.out.print( p.data + " " ) ;
print_rec_depth_first_pre_order( p.left ) ;
print_rec_depth_first_pre_order( p.right ) ;
}
}
// 深さ優先探索(前順)
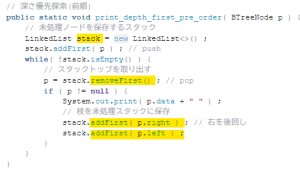
public static void print_depth_first_pre_order( BTreeNode p ) {
// 未処理ノードを保存するスタック
LinkedList stack = new LinkedList<>() ;
stack.addFirst( p ) ; // push
while( !stack.isEmpty() ) {
// スタックトップを取り出す
p = stack.removeFirst() ; // pop
if ( p != null ) {
System.out.print( p.data + " " ) ;
// 枝を未処理スタックに保存
stack.addFirst( p.right ) ; // 右を後回し
stack.addFirst( p.left ) ;
}
}
}
public static void main(String[] args) throws Exception {
BTreeNode top =
new BTreeNode( 42 ,
new BTreeNode( 27 ,
new BTreeNode( 13 , null , null ) ,
new BTreeNode( 38 , null , null ) ) ,
new BTreeNode( 72 ,
new BTreeNode( 64 , null , null ) ,
new BTreeNode( 81 , null , null ) ) ) ;
// 再帰による深さ優先探索(前順)
print_rec_depth_first_pre_order( top ) ;
System.out.println() ;
// スタックを使った深さ優先探索(前順)
print_depth_first_pre_order( top ) ;
System.out.println() ;
}
}
- 2分探索木の深さ優先探索、幅優先探索(Paiza.io)
幅優先探索
同じように、未処理のノードを待ち行列に保存しながら、ノードに対する処理を行うことでも、すべての木に対する処理が記述できる。この場合、根本の処理をすべて終えてから、末端に対する処理が行われる。このような処理は幅優先探索と呼ぶ。
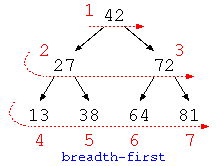
幅優先探索の処理と、前順の深さ優先探索を比べると、ノードを覚えるデータ構造に待ち行列を使う(幅優先探索)か、スタックを使う(深さ優先探索)の違いしかない。
 |
 |
幅優先探索は、ゲームの戦略で先読みを行う場合に用いられるが、チェス・将棋・囲碁といったすべての先読みを行うと手数が爆発的に増加するため、不利な戦略の先読みを途中で打ち切る必要がある場合に有用である。
public class Main {
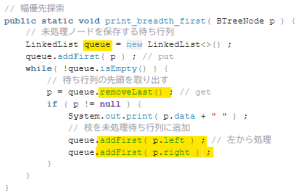
// 幅優先探索
public static void print_breadth_first( BTreeNode p ) {
// 未処理ノードを保存する待ち行列
LinkedList queue = new LinkedList<>() ;
queue.addFirst( p ) ; // put
while( !queue.isEmpty() ) {
// 待ち行列の先頭を取り出す
p = queue.removeLast() ; // get
if ( p != null ) {
System.out.print( p.data + " " ) ;
// 枝を未処理待ち行列に追加
queue.addFirst( p.left ) ; // 左から処理
queue.addFirst( p.right ) ;
}
}
}
public static void main(String[] args) throws Exception {
BTreeNode top = (略) ;
// 幅優先探索で表示
print_breadth_first( top ) ;
System.out.println() ;
}
}
深さ優先探索(中順)
2分探索木のようなデータで、昇順で並べて表示する必要がある場合、再帰呼び出しのプログラムでは、「左枝の処理、ノードへの処理、右枝の処理」の順で記述する必要がある。このような深さ優先探索は中順(in-order)と呼ばれる。しかし、先に説明した再帰による深さ優先探索(前順/pre-order)では、「ノードへの処理、左枝の処理、右の枝の処理」で記述されている。
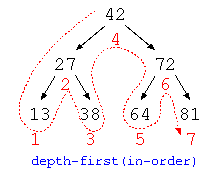
スタックを用いた深さ優先探索で、2分探索木の昇順のように中順で処理を行うには、未処理のノードの保存順序に工夫が必要となる。
import java.util.*;
public class Main {
// 再帰呼び出しによる木の操作 = 深さ優先探索(中順)
public static void print_rec_depth_first_in_order( BTreeNode p ) {
if ( p != null ) {
print_rec_depth_first_in_order( p.left ) ;
System.out.print( p.data + " " ) ;
print_rec_depth_first_in_order( p.right ) ;
}
}
// 深さ優先探索(中順)
public static void print_depth_first_in_order( BTreeNode p ) {
// 未処理ノードを保存するスタック
LinkedList stack = new LinkedList<>() ;
for( ;; ) {
// ノードを保存しながら左末端まで進む
while( p != null ) {
stack.addFirst( p ) ;
p = p.left ;
}
// 未処理が残っていないなら終了
if ( stack.isEmpty() )
break ;
// スタックトップを取り出す
p = stack.removeFirst() ; // pop
System.out.print( p.data + " " ) ;
p = p.right ;
}
}
public static void main(String[] args) throws Exception {
BTreeNode top = (略) ;
// 再帰による深さ優先探索(中順)
print_rec_depth_first_in_order( top ) ;
System.out.println() ;
// スタックを使った深さ優先探索(中順)
print_depth_first_in_order( top ) ;
System.out.println() ;
}
}