コンパイラの処理の流れ
構文の構造を表すために、2分木を使うという話をこの後に行うが、その前にコンパイラが機械語を生成するまでの処理の流れについて説明をする。
Cコンパイラのソース ↓ プリプロセッサ (#define,#includeなどの処理) ↓ コンパイラ ・字句解析(ソースコードをトークンに切り分ける) ・構文解析(トークンから構文木を生成) ・最適化(命令を効率よく動かすために命令を早い命令に書き換え) ・コード生成(構文木から中間コードを生成) | | リンカでライブラリと結合 (+)←---ライブラリ ↓ 機械語
2項演算と構文木
演算子を含む式が与えられたとして、古いコンパイラではそれを逆ポーランド変換して計算命令を生成していた。しかし最近の複雑な言語では、計算式や命令を処理する場合、その式(または文)の構造を表す2分木(構文木)を生成する。。
+ / \ 1 * / \ 2 3
演算子の木のノードで、末端は数値であることに注目し、右枝・左枝がNULLなら数値(data部にはその数値)、それ以外は演算子(data部には演算子の文字コード)として扱うとして、上記の構文木のデータを作る処理と、その構文木の値を計算するプログラムを示す。
struct Tree {
int data ;
struct Tree* left ;
struct Tree* right ;
} ;
struct Tree* tree_int( int x ) // 数値のノード
{
struct Tree* n ;
n = (struct Tree*)malloc( sizeof( struct Tree ) ) ;
if ( n != NULL ) {
n->data = x ;
n->left = n->right = NULL ;
}
return n ;
}
struct Tree* tree_op( int op , // 演算子のノード
struct Tree* l , struct Tree* r ) {
struct Tree* n ;
n = (struct Tree*)malloc( sizeof( struct Tree ) ) ;
if ( n != NULL ) { // ~~~~~~~~~~~~~~~~~~~~~(D)
n->data = op ;
n->left = l ;
n->right = r ;
}
return n ;
}
// 与えられた演算子の木を計算する関数
int eval( struct Tree* p ) {
if ( p->left == NULL && p->right == NULL ) {
// 数値のノードは値を返す
return p->data ;
} else {
// 演算子のノードは、左辺値,右辺値を求め
// その計算結果を返す
switch( p->data ) {
case '+' : return eval( p->left ) + eval( p->right ) ;
case '*' : return eval( p->left ) * eval( p->right ) ;
} // ~~~~~~~~~~~~~~~(E) ~~~~~~~~(F)
}
}
void main() {
struct Tree* exp = // 1+(2*3) の構文木を生成
tree_op( '+' ,
tree_int( 1 ) ,
tree_op( '*' ,
tree_int( 2 ) ,
tree_int( 3 ) ) ) ;
printf( "%d¥n" , eval( exp ) ) ;
}
理解度確認
- 上記プログラム中の(A)~(F)の型を答えよ。
2分探索木の考え方を拡張したものでB木があり、データベースシステムではB木を基本としたデータ構造が活用されている。
B木の構造
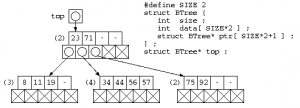
2分木では、データの増減で木の組換えの発生頻度が高い。そこで、1つのノード内に複数のデータを一定数覚える方法をとる。B木では、位数=Nに対し、最大2N個のデータ d0, … , d2N-1 と、2N+1本のポインタ p0, … , p2N から構成される。pi の先には、di-1< x < di を満たすデータが入った B木のノードを配置する。ただし、データの充填率を下げないようにするため、データは最小でもN個、最大で2N個を保存する。下図は位数2のB木の例を示す。
B木からデータの検索
データを探す場合は、ノード内のデータ di の中から探し、見つからない場合は、ポインタの先のデータを探す。位数がある程度大きい場合、ノード内の検索は2分探索法が使用できる。また、1つのノード内の検索が終われば、探索するデータ件数は、1/N〜1/2Nとなることから、指数的に対象件数が減っていく。よって、検索時間のオーダは、O( log N ) となる。
B木へのデータの追加
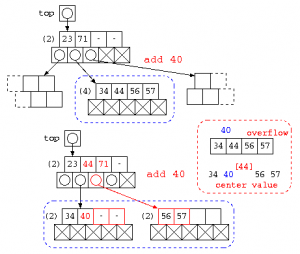
B木にデータを追加する場合は、ノード内に空きがあれば、単純にデータの追加を行う。ノード内のデータが2N個を越える場合は、以下のような処理を行う。
ノード内のデータと追加データを並べ、その中央値を選ぶ。この中央値より大きいデータは、新たにつくられたノードに移す。中央値のデータは上のノードに追加処理を行う。このような方法を取ることで、2分木のような木の偏りが作られにくい構造となるようにする。
データを削除する場合も同様に、データ件数がN個を下回る場合は、隣接するノードからデータを取ってくることで、N個を下回らないようにする。
B木とデータベース
このB木の構造は、一般的にデータベースのデータを保存するために広く利用されている。
データベースシステムでは、データを効率よく保存するだけでなく、データの一貫性が保たれるように作られている。
例えば、データベースのシステムが途中でクラッシュした場合でも、データ更新履歴の情報を元にデータを元に戻し、データを再投入して復旧できなければならない。データを複数の所からアクセスした場合に、その順序から変な値にならないように、排他制御も行ってくれる。
データベースで最も使われているシステムは、データすべてを表形式で扱うリレーショナル・データベースである。
((リレーショナル・データベースの例)) STUDENT[] RESULT[] ID | name | grade | course ID | subject | point -----+----------+-------+-------- -----+---------+------- 1001 | t-saitoh | 5 | EI 1001 | math | 83 1002 | sakamoto | 4 | E 1001 | english | 65 1003 | aoyama | 4 | EI 1002 | english | 90 外部キー ((SQLの例 2つの表の串刺し)) -- 60点以上の学生名,科目名,点数を出力 -- select STUDENT.name, RESULT.subject, RESULT.point --射影-- from STUDENT , RESULT --結合-- where STUDENT.ID == RESULT.ID -- 串刺し -- --選択-- and RESULT.point >= 60 ; ((上記SQLをC言語で書いた場合)) for( st = 0 ; st < 3 ; st++ ) // 結合(from) for( re = 0 ; re < 3 ; re++ ) if ( student[ st ].ID == result[ re ].ID // 選択(where) && result[ re ].point >= 60 ) printf( "%s %s %d" , // 射影(select) student[ st ].name , result[ re ].subject , result[ re ].point ) ;
- 学生と成績(Paiza.ioでSQL)
- sql-mapping.cxx
B+木
データベースの処理では、目的のデータを O(log N) で見つける以外にも、全データに対する処理も重要である。この場合、全てのデータに対する処理では、単純なB木では再帰呼び出しが必要となる。しかし、他の表でも再帰処理を伴うと、プログラムは複雑になってしまう。
そこで、B木のデータを横方向に並べて処理を行う場合に、その処理が簡単になるように B+木が用いられる。
この方法では、末端のノードは、隣接するノードへのポインタを持つ。下図で示すB+木では、青で示す検索用のB木の部分と、赤で示す順次処理を行うためのシーケンスセットの部分から構成される。