情報制御基礎の授業を通して、入力値を制御するため、コンピュータを使う場合の数値処理の基礎的な話として、信号の平滑化を説明してきたので、最後に差分について説明をする。また、実際には、入力値を制御に利用する一般的な構成のフィードバック制御について説明する。
変化の検出
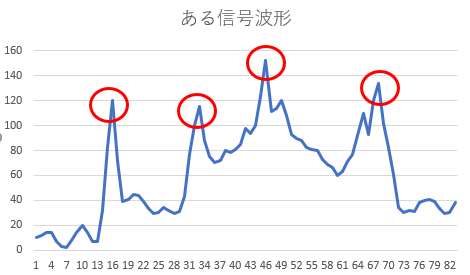
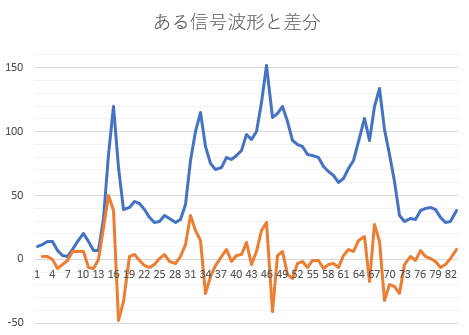
例えば、以下のような若干のノイズが混ざった入力信号が与えられたとする。この波形で「大きな山が何ヶ所ありますか?」と聞かれたら、いくつと答えるべきであろうか?山の判断方法は色々あるが、4カ所という答えは、1つの見方であろう。では、この4カ所という判断はどうすればいいだろうか?
こういった山の数を数えるのであれば、一定値より高いか低いか…という判断方法もあるだろう。この絵であれば、15ステップ目、32ステップ目付近は、100を越えていることで、2つの山と判断できるだろう。
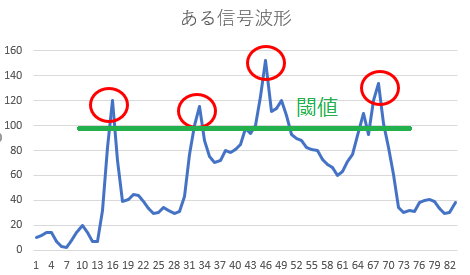
こういった予め決めておいた値より「上か?/下か?」で判断するときの基準値は、しきい値(閾値:threshold)と呼ぶ。
しかし、この閾値では、40ステップ目から50ステップ目も100を越えており、以下のようなプログラムを書いたら、40ステップ目~50ステップ目すべてをカウントしてしまう。
#define THRESHOLD 100
int x[ 100 ] = {
// 波形のデータが入っているとする。
} ;
int count = 0 ;
for( int i = 0 ; i < 100 ; i++ ) {
if ( x[i] >= THRESHOLD )
count++ ;
}
また、65ステップ目の小さな山も1個とカウントしてしまう。
この問題を避けるために、閾値を130にすると、今度は最初の2つの山をカウントできない。どうすれば、山の数をうまくカウントできるのだろうか?
差分を求める
前述のような問題で山の数を数える方法を考えていたが、数学で山を見つける時には、何をするだろうか?
数学なら、山や谷の頂点を求めるのならば、微分して変化量が0となる場所を求めることで、極大値・極小値を求めるだろう。そこで、山を見つけるために入力値の変化量を求めてみよう。
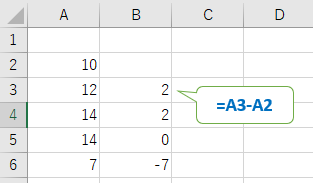
表計算ソフトで差分を計算するのであれば、セルに図のような式を入力すればいいであろう。このようなデータ点で前の値との差を差分と呼ぶ。数学であれば、微分に相当する。
このグラフを見ると、波形が大きく増加する部分で、差分が大きな正の値となる。さらに波形が大きく減少する部分で差分が負の大きな値となる。特にこのデータの場合、山と判断したい部分は差分が20以上の値の部分と定義することも考えられる。
#define TH_DIFF 20
int x[ 100 ] = {
// 波形のデータが入っているとする。
} ;
int count = 0 ;
for( int i = 0 ; i < 100 ; i++ ) {
if ( x[i] - x[i-1] >= TH_DIFF
&& x[i+1] - x[i] <= -TH_DIFF )
count++ ;
}
しかし、このプログラムでは、山の数をうまくカウントしてくれない。うまく、山の数を数えるためには、差分の値を山と判断するための閾値(この場合は20)を調整することになるだろう。
移動平均との差
前回の講義で示したデータの例で、移動平均を取ると分かる事例ということで、船につけられた加速度センサーで、長い周期の波による船の揺れと、短い周期のエンジンによる振動があったとき、エンジンの振動を移動平均で取り除くことができるという事例を示した。
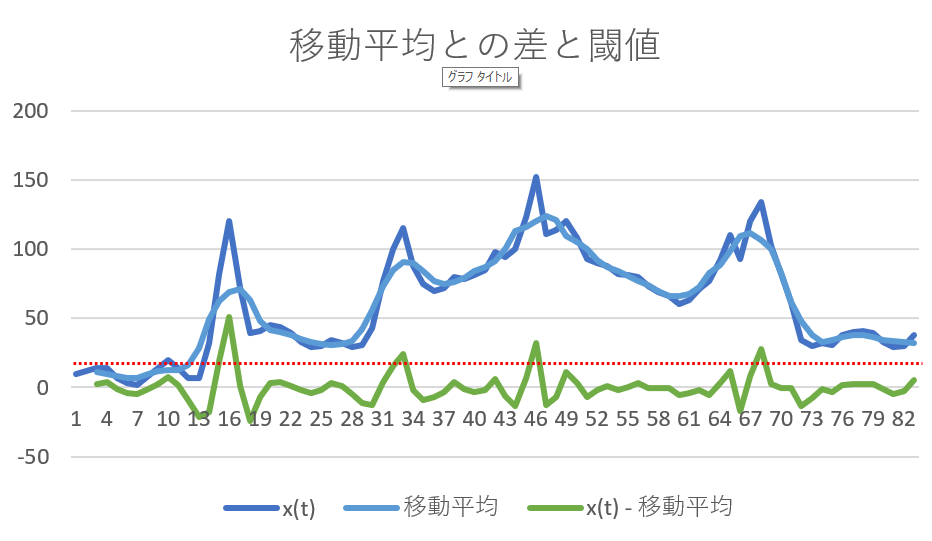
これを逆手にとれば、元の信号と移動平均の差を取れば、エンジンの振動だけを取り出すことも可能となる。以下は、前の事例で、前後5stepの移動平均(水色線)と元信号(青線)の差をとったものが緑線となっている。このような方法をとれば、元信号の短い周期の変動を抽出することができる。
制御工学の概要
以下に、制御工学ではどのようなことを行うのか、概要を述べる。
ここで紹介する制御理論は、古典制御理論と呼ばれる。
制御工学では、入力値と、何らかの処理を施し出力値
が得られるシステムで、どのように制御するかを考える。
例えば、電気ポットの温度制御をする場合、設定温度の値を入力値とし、何らかの処理を行い、出力となるヒーターの電流を制御し、最終的には温度
が測定される。ヒーターは、設定温度
と温度計の値
の差
に応じて電流量を変化させる。このように一般的な制御では、最終的な温度が入力に戻っている。このように目標値に近づけるために、目標値との差に応じて制御することをフィードバック制御という。
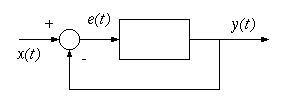
制御の仕方には様々な方法があるが、 がとある時間で0からYに変化した場合を考える。入力と出力で制御された波形の例を示す。
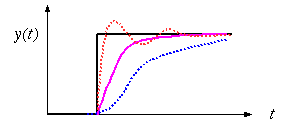
この波形では、黒のように入力値が変化した場合、それに追いつこうと出力が変化する。(1)理想的には、速やかに追いつく赤のように変化したい。しかし、(2)慎重に制御をする人なら、変化への制動が大きい過制動(青点線)となり、目標値に追いつくまでに時間がかかる。(3)一方、すこしでもずれたら直そうとする人なら、時間的には速い反応ができるかもしれないが、目標値を追い越したり、増えすぎ分を減らしすぎたりして脈動する過制御(赤点線)となるかもしれない。
PID制御
目標値、出力
、ずれ(偏差)
、制御量
とした時、基本的なフィードバック制御として偏差の使い方によってP動作,I動作,D動作がある。参考 Wikipedia PID制御
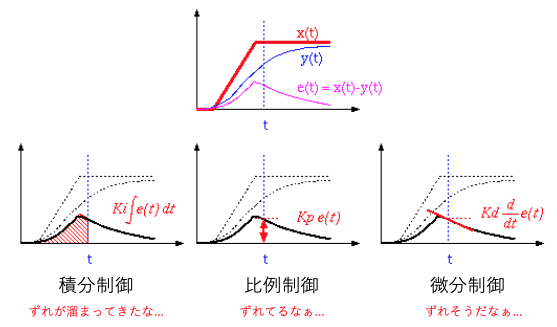
比例制御(P制御)
偏差に比例した制御を行う方式(を比例ゲインと呼ぶ)
今年のコロナ騒動を例にとるならば、比例制御は、今日の感染者数y(t)と目標としたい感染者数x(t)の差に応じて、対策の強さu(t)を決めるようなもの。
積分制御(I制御)
偏差のある状態が長い時間続く場合、入力値の変化を大きくすることで目標値に近づけるための制御。(は積分ゲイン)
積分制御は、目標の感染者数x(t)を感染者数y(t)が超えた累積患者数に応じて、対策を決めるようなもの。
移動平均は、一定範囲の値の和(を範囲のデータ数で割ったもの)であり、積分制御は移動平均の値に応じて制御するとみなすこともできる。
微分制御(D制御)
急激な出力値の変化が起こった場合、その変化の大きさに応じて妨げようとする制御。(は微分ゲイン)
微分制御は、目標数と感染者数の差が、前日よりどのぐらい増えたか(患者の増減の量:変化量)に応じて、対策を決めるようなもの。
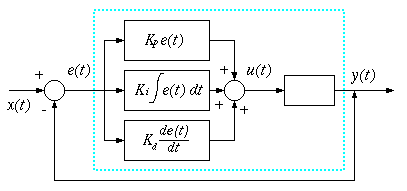
PID制御
上記のI制御やD制御だけでは、安定させることが難しいので、これらを組み合わせたPID制御を行う。
この中で、の値は、制御が最も安定するように調整を行うものであり、数値シミュレーションや、ステップ応答を与えた時の時間的変化を測定して調整を行う。