データ処理において、配列は基本的データ構造だが、動的メモリ確保の説明で述べたように、基本の配列では大きさを変更することができない。これ以外にも、配列は途中にデータを挿入・削除を行う場合、の処理時間を伴う。以下にその問題点を整理し、その解決策であるリスト構造の導入の説明を行う。

配列の利点と欠点

今までデータの保存には、配列を使ってきたが、配列は添字で場所を指定すれば、その場所のデータを簡単に取り出すことができる。しかし、配列には苦手な処理がある。

例えば、配列の中から目的のデータを高速に探す方式として、2分探索法を用いる。処理に要する時間としては となる。

// この関数は見つかったら、見つかった場所、見つからない場合は -1 を返す。
int find( int array[] , int left , int right , int key ) {
   // データは left から right-1までに入っているとする。
   while( left < right ) {
      int mid = (left + right) / 2 ; // 中央の場所
      if ( array[ mid ] == key )
         return mid ;                // 見つかった
      else if ( array[ mid ] > key )
         right = mid ;               // 左半分にある
      else
         left = mid + 1 ;            // 右半分にある
   }
   return -1 ; // 見つからない
}

int a[] = { 12 , 34 , 41 , 53 , 62 , 79 , 80 } ;
int main() {
   int ans = find( a , 0 , 7 , 62 ) ; // 配列 a[] から 62 を探す
   printf( "%d¥n" , ans ) ;           // 4が表示される
   return 0 ;
}

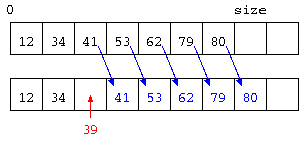
しかし、この配列の中に新たに要素を追加しようとするならば、データは昇順に並んでいる必要があることから、以下のようになるだろう。

void entry( int array[] , int* psize , int key ) {
   // データを入れるべき場所を探す処理
   for( int i = 0 ; i < *psize ; i++ ) // O(N) の処理だけど、
      if ( array[ i ] > key )          // O(log N) でも書けるけど
         break ;                       // 今回は単純に記載する。
   if ( i < *psize ) {
      // 要素を１つ後ろにずらす処理(A)
      for( int j = *psize ; j > i ; j-- ) //  O(N)の処理
         array[ j ] = array[ j - 1 ] ;
      array[ i ] = key ; 
   } else {
      array[ *psize ] = key ;
   }
   (*psize)++ ;
}
   /// よくある間違い ///
   /// 上記処理の(A)の部分を以下のように記載した ///
   /// 問題点はなにか答えよ ///
   //   for( int j = i ; j < size ; j++ )
   //      array[ j + 1 ] = array[ j ] ;
   //   array[ i ] = key ;

int main() {
   int a[ 100 ] ;
   int size = 0 ;
   int x ;
   // 入力された値を登録していく繰り返し処理
   while( scanf( "%d" , &x ) == 1 ) {
      // x を追加する。
      entry( a , &size , x ) ;
   }
   return 0 ;
}

これで判るように、昇順に並んだ配列にデータを追加する場合、途中にデータを入れる際にデータを後ろにずらす処理が発生する。

この例は、データを追加する場合であったが、不要となったデータを取り除く場合にも、データの場所の移動が必要である。

このことから、昇順に並べられた配列は、データの追加処理の発生頻度が少ない場合は2分探索法で効率が良いが、データの追加や削除が頻繁に発生する時はあまり効率が良くない。

順序が重要なデータ列で途中へのデータ挿入削除を高速化

例えば、アパート入居者に回覧板を回すことを考える。この中で、入居者が増えたり・減ったりした場合、どうすれば良いか考える。
以下の説明のような方法であれば、自分の所に回覧板が回ってきたら、次の入居者の部屋番号さえわかっていれば、スムーズに回覧板を回すことができる。

  101   102   103   104   105   106   アパートの番号
[ 105 | 106 |  -1 | 102 | 104 | 103 ] 回覧板を回す次の人の部屋番号

101号室の次は、105号室、
105号室の次は、104号室、
  :
106号室の次は、103号室、
103号室の次は、おしまい(-1)

このように「次のデータの場所」という概念を使うと、データの順序を持って扱うことができる。これをプログラムにしてみよう。

struct LIST {
   int data ;  // 実際のデータ
   int next ;  // 次のデータの配列の添字
} ;

struct LIST array[] = {
   /*0*/ { 11 ,  2 } , 
   /*1*/ { 67 ,  3 } ,  // 末尾にデータ34を加える
   /*2*/ { 23 ,  4 } ,  // { 23 , 5 } ,
   /*3*/ { 89 , -1 } ,  // 末尾データの目印
   /*4*/ { 45 ,  1 } ,
   /*5*/ {  0 ,  0 } ,  // { 34 , 4 } ,
} ;

int main() {
   for( int idx = 0 ; idx >= 0 ; idx = array[ idx ].next ) {
      printf( "%d\n" , array[ idx ].data ) ; 
   }
   // 11,23,45,67,89,終

   array[5].data = 34 ;
   array[5].next =  4 ; // /*4*/ {45,1}
   array[2].next =  5 ;
   // O(1)で1件追加

   for( int idx = 0 ; idx >= 0 ; idx = array[ idx ].next ) {
      printf( "%d\n" , array[ idx ].data ) ;
   }
   // 11,23,[[34]],45,67,89,終
   return 0 ;
}

この方法を取れば、途中にデータ入れたり、抜いたりする場合に、データの移動を伴わない。(O(N)の処理が発生しない)

しかし、配列をベースにしているため、配列の上限サイズを超えて格納することはできない。そこで、必要に応じてメモリを確保するテクニックを導入する。