表計算ソフトの使い方(絶対参照・相対参照)
今日の表計算ソフトを使った演習では、下記のサンプルファイルを練習に使うので、Teamsで参照してください。
前回課題の答え合わせ
前回のレポートでは、sin(83度)(例)といった数値の有効数字を考えるというものを考えてもらったので、この有効数字をどう記載すべきか考えてみる。
課題を示す Excel ファイルでは、75度~89度あたりの角度で出題をするようにしてあった。注意しないといけない点は、sinは90度に近づくほど、1に近づく。このため、0.99…といった数値が求まるが、角度がちょっと変化しても、0.99といった部分はほぼ変化しない。だから、83が有効数字2桁ということで、0.99 といった有効数字2桁の書き方では、ちょっと不十分かもしれない。
そこで、83度(有効数字2桁)が小数点以下を丸められた数値と仮定する。この場合、元の数値は 82.5度~83.5度 の可能性がある。これらの値のsinを計算すると、0.9914から0.9935の間であり、小数点以下3桁目は、1~3 の値であり、結果を 0.992 (有効数字3桁) と記載しても良いかもしれない。
sin(82.5°) = 0.991444861 sin(83.0°) = 0.992546152 sin(83.5°) = 0.993571856
表計算ソフトの使い方
情報制御基礎では、プログラムで計算する所を、Excel のような表計算ソフトを用いて検証してもらったりする予定なので、Excel で計算式を使う方法を説明する。
セルの場所と簡単な式
簡単な、品名・単価・個数・価格の表を考える。以下の表のように、列の名前と、品名・単価・個数まで入力した後、単価と個数をかけた価格を求めるとする。
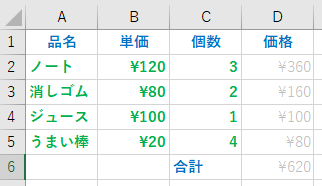
Excel では、表の列には左から、A,B,C,D… , 表の行には上から1,2,3,4,5 と番号が振られていて、特定の列・特定の行のデータを表す時には、列行を組み合わせ、A1に品名、B3に¥80、C5に4 が入っている。
例えば、D2 に、ノート単価120円、ノート個数3個をかけた値を入れたい場合は、D2の場所に、
=B2*C2
を書き込めば、その場所には360が表示される。
先頭の”=”を入力した後、該当する”B2″の場所をクリックするなりカーソルを操作すると、カーソルのセルの場所”B2″が自動的に入力される。さらに”*”を入力した後、”C2″の場所をクリックすれば”C2″が入力される。
Excelでは、入力する文字列の先頭が”=”の場合は、残り部分は計算式として扱われる。
D3には、”=B3*C3″を入力すれば、160 が表示される。しかし、この様な式を何度も入力するのは面倒である。
この場合、セル・カーソルを、D2 に合わせ、[右ボタン]-[コピー]を行い、D3 で[右ボタン]-[貼り付けオプション]-[貼り付け]を行えば、”=B3*C3″が入力される。
ここで注意しないといけないのが、式を張り付ける場合には、貼り付け先のセルの場所が一つ下の行なので、行番号を表す2の部分が1つ下の行番号3に書き換えられて、貼り付けが行われる。(相対参照)
関数式
例えば、下左図のような、数字とその平方根の表を作る場合、A2 に 1、B2に =sqrt( A2 ) を入力、A3 に =A2+1 を入力したあと、B2の式をB3にコピー&ペーストし、A3,B3 を A4~A6にペーストすればいい。
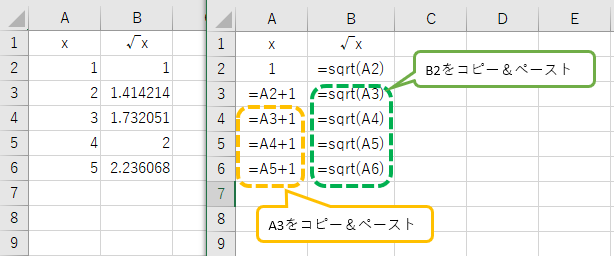
B2に入力したような、sqrt( A2 ) のようなものは、関数式と呼ばれる。
また、A3,B3 といった複数の行・列をまとめた範囲を示す時は、A3:B3 といった表記方法であらわす。
絶対参照と相対参照
最初の例に戻って、単価と個数の積で今度は税率を加えて計算する例を考える。また、税率は後で変化するかもしれないので、B1 のセルに税率を記入しておく場合を考える。
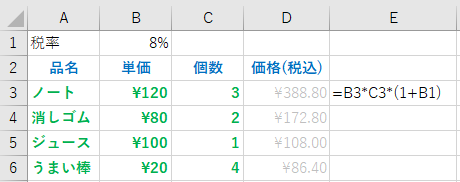
この場合、D3 には、” =B3*C3*(1+B1) ” を入力すればいい。
ただ、このように式を入力すると、D3 の計算式を、D4,D5,D6 にコピーすると、セル D4 には =B4*C4*(1+B2) が入力されてしまい、B2 には単価という文字が記載されているため、正しい結果が求まらない。
こういった場合には、絶対参照を用いる。D3 に記入する式を
=B3*C3*(1+$B$2)
とし、この D3 の式を D4 にコピー&ペーストすると、列記号、行番号の前に$がついた部分の式は、貼り付け場所に応じて変化しない。
このような、$B$2 といったセルの参照は、絶対参照と呼ぶ。これに対し、B2 といったセル参照は、貼り付け場所に応じて書き換えられるので、相対参照と呼ぶ。
絶対参照と相対参照が混ざった、$B2, B$2 といった書き方もある。
式の入力時に[F4ボタン]を押す度に、B2→$B$2→B$2→$B2→B2 と変化する$B2 は、式をコピーすると列部分はBのまま、行部分は場所に合わせて変化する。
B$2 は、式をコピーすると列部分は場所に合わせて変化し、行部分は2のままとなる。
レポート課題(第5回)
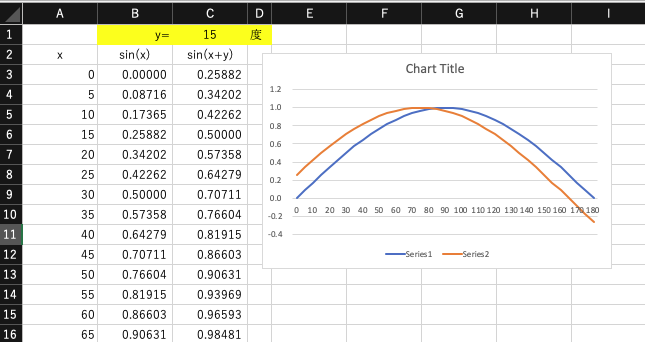
Excel で、xを0〜180度まで変化させたときのsin(x),位相をyとした時のsin(x+y)の値の表を作り、グラフ機能で表示せよ。A列は角度・B列はsin(x)・C列はsin(x+y)の値とし、yの値は”C1″に保存されているものとする。
この時、計算式の入力をどのように行なったのか(相対参照や絶対参照をどのように使ったのか)説明を、グラフの下に入力欄を設け記入せよ。
なお、Excel の sin() 関数は、引数がラジアンで入力する必要があるので、計算式には注意せよ。
そして出来上がった Excel のファイルを、Teams のこちらのフォルダに提出せよ。
UMLの概要と構造図
前回の授業でUMLの概要について説明を行ったが、専攻科の休講日だったようなので、UMLの概要をおさらいした後、UMLの構造図の説明を行う。
UML(Unified Modeling Language)記法が生まれるまで
巨大なプロジェクトでプログラムを作る場合、対象となるシステムを概念として表現する場合、オブジェクト指向分析(OOA: Object Oriented Analysis)やオブジェクト指向設計(OOD: Object Oriented Design)とよばれるソフトウェア開発方法が重要となる。(総称して OOAD – Object Oriented Analysis and Design)
これらの開発方法をとる場合、(1)自分自身で考えを整理したり、(2)グループで設計を検討したり、(3)ユーザに仕様を説明したりといった作業が行われる。この時に、自分自身あるいはチームメンバーあるいはクライアントに直感的に図を用いて説明する。この時の図の書き方を標準化したものが UML であり、(a)処理の流れを説明するための振る舞い図(以前であればフローチャートやPAD)と、(b)データ構造を説明するための構造図を用いる。
UMLは、ランボーによるOMT(Object Modeling Technique どちらかというとOOA中心)と、 ヤコブソンによるオブジェクト指向ソフトウェア工学(OOSE)を元に1990年頃に 発生し、ブーチのBooch法(どちらかというとOOD中心)の考えをまとめ、 UML(Unified Modeling Language)としてでてきた。
UMLでよく使われる図を列記すると、以下の物が挙げられる。
- 構造図
- クラス図
- コンポーネント図
- 配置図
- オブジェクト図
- パッケージ図
- 振る舞い図
- アクティビティ図
- ユースケース図
- ステートチャート図(状態遷移図)
- 相互作用図
- シーケンス図
- コミュニケーション図(コラボレーション図)
UMLを正しく使うことができるようになれば、UMLで仕様書を書けばそれがそのままプログラムになることが理想的な姿かもしれない。ソフトウェア開発やソフトウェアの保守にソフトウェアツールを利用することは、CASE(Computer Aided Software Engineering)と呼ばれ、そのようなツールをCASEツールと呼ぶ。地元福井の永和システムマネジメントでは、astar* というCASEツールを開発している。
UMLの構造図の書き方の説明。 詳しくは、参考ページのUML入門などが、分かりやすい。
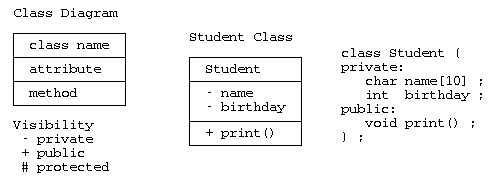
クラス図
クラス図は、構造図の中の基本的な図で、 枠の中に、上段:クラス名、中段:属性(要素)、下段:メソッド(関数)を記載する。 属性やメソッドの可視性を示す場合は、”-“:private、”+”:public、”#”:protected 可視性に応じて、”+-#”などを記載する。
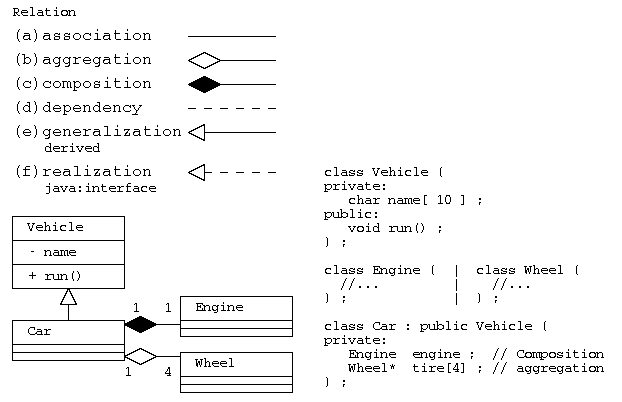
関連
クラスが他のクラスと関係がある場合には、その関係の意味に応じて、直線や矢印で結ぶ。
(a)関連(association):単純に関係がある場合、
(b)集約(aggregation):部品として持つが、弱い結びつき。関係先が消滅しても別に存在可能。(has-a)
(c)コンポジション(composition):部品として持つが強い結びつき。関係先と一緒に消滅。(has-a)
(d)依存(dependency):依存関係にあるだけ
(e)派生(generalization):派生・継承した関係(is-a)
(f)実現(realization): Javaでのinterfaceによる多重継承
上図の例では、乗り物クラスVehicleから自動車Carが派生し(CarからVehicleへの三角矢印―▷)、 自動車は、エンジン(Engine)を部品として持つ(EngineからCarへのひし形矢印―◆)。エンジンは車体と一緒に廃棄なら、コンポジション(C++であれば部品の実体を持つ)で実装する。
自動車は、同じく車輪(Wheel)を4つ持つが、自動車を廃棄してもタイヤは別に使うかもしれないので、集約(部品への参照を持つ)で実装する(WheelからCarへのひし形矢印―◇)。 集約で実装する場合は、C++などであれば、ポインタで部品を持ち、部品の廃棄(delete)は、別に行うことになる。
Javaなどのプログラム言語では、オブジェクトはデータの実体へのポインタで扱われるため、コンポジションと集約を区別して表現することは少ない。
is-a 、has-a の関係
前の課題でのカモノハシクラスで、羽や足の情報をどう扱うべきかで、悩んだ場合と同じように、 クラスの設計を行う場合には、部品として持つのか、継承として機能を持つのか悩む場合がある。 この場合には、“is-a”の関係、“has-a”の関係で考えると、部品なのか継承なのか判断しやすい。
たとえば、上の乗り物(Vehicle)クラスと、車(Car)のクラスは、”Car is-a Vehicle” といえるので、is-a の関係。 “Car is-a Engine”と表現すると、おかしいことが判る。 車(Car)とエンジン(Engine)のクラスは、”Car has-a Engine”といえるので、has-a の関係となる。 このことから、CarはVehicleからの派生であり、Carの属性としてEngineを部品として持つ設計となる。
ER図
UMLではないが、オブジェクト図に近いものとしてER図がある。これはリレーショナルデータベースの設計が正しいか確認しながら設計するための図で、Entity(実体)とRelation(関連)を相互に線で結んだもので、最近のER図の書き方は、かなりクラス図の書き方に似ている。
オブジェクト図
クラス図だけで表現すると、複雑なクラス関係では、イメージが分かりづらい場合がでてくる。 この場合、具体的な値を図に書き込んだオブジェクトで表現すると、説明がしやすい場合がある。 このように具体的な値で記述するクラス図は、オブジェクト図と言う。 書き方としては、クラス名の下に下線を引き、中段の属性の所には具体的な値を書き込んで示す。
その他の構造図
パッケージ図
パッケージ図は、クラス図をパッケージ毎に分類して記載する図。 パッケージのグループを、フォルダのような図で記載する。

IT専科から引用
コンポーネント図とコンポジット構造図
コンポジット構造図は、クラスやコンポーネントの内部構造を示すもので、コンポーネント図は、複数のクラスで構成される処理に、 インタフェースを用意し、あたかも1つのクラスのように扱ったもの。 接続するインタフェースを飴玉と飴玉を受けるクチのイメージで、提供側を◯───で表し、要求側を⊃──で表す。
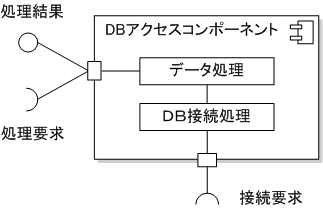
IT専科から引用
配置図
配置図は、システムのハードウェア構成や通信経路などを表現するための図。 ハードウェアは直方体の絵で表現し、 デバイスの説明は、”≪device≫”などを示し、実行環境には、”≪executionEnvironment≫” などの目印で表現する。
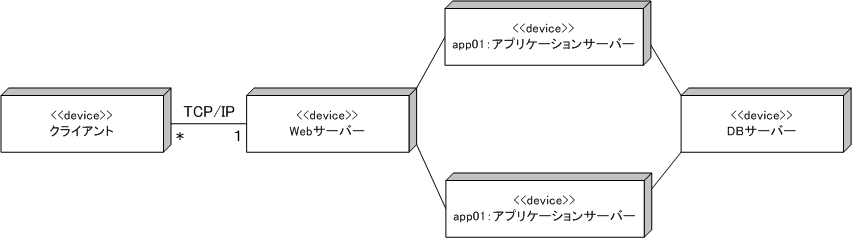
IT専科から引用
リスト構造の導入
データ処理において、配列は基本的データ構造だが、動的メモリ確保の説明で述べたように、基本の配列では大きさを変更することができない。これ以外にも、配列は途中にデータを挿入・削除を行う場合、の処理時間を伴う。以下にその問題点を整理し、その解決策であるリスト構造の導入の説明を行う。
配列の利点と欠点
今までデータの保存には、配列を使ってきたが、配列は添字で場所を指定すれば、その場所のデータを簡単に取り出すことができる。しかし、配列には苦手な処理がある。
例えば、配列の中から目的のデータを高速に探す方式として、2分探索法を用いる。処理に要する時間としては となる。
// この関数は見つかったら、見つかった場所、見つからない場合は -1 を返す。
int find( int array[] , int left , int right , int key ) {
// データは left から right-1までに入っているとする。
while( left < right ) {
int mid = (left + right) / 2 ; // 中央の場所
if ( array[ mid ] == key )
return mid ; // 見つかった
else if ( array[ mid ] > key )
right = mid ; // 左半分にある
else
left = mid + 1 ; // 右半分にある
}
return -1 ; // 見つからない
}
int a[] = { 12 , 34 , 41 , 53 , 62 , 79 , 80 } ;
int main() {
int ans = find( a , 0 , 7 , 62 ) ; // 配列 a[] から 62 を探す
printf( "%d¥n" , ans ) ; // 4が表示される
return 0 ;
}
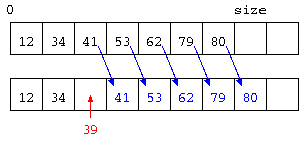
しかし、この配列の中に新たに要素を追加しようとするならば、データは昇順に並んでいる必要があることから、以下のようになるだろう。
void entry( int array[] , int* psize , int key ) {
// データを入れるべき場所を探す処理
for( int i = 0 ; i < *psize ; i++ ) // O(N) の処理だけど、
if ( array[ i ] > key ) // O(log N) でも書けるけど
break ; // 今回は単純に記載する。
if ( i < *psize ) {
// 要素を1つ後ろにずらす処理(A)
for( int j = *psize ; j > i ; j-- ) // O(N)の処理
array[ j ] = array[ j - 1 ] ;
array[ i ] = key ;
} else {
array[ *psize ] = key ;
}
(*psize)++ ;
}
/// よくある間違い ///
/// 上記処理の(A)の部分を以下のように記載した ///
/// 問題点はなにか答えよ ///
// for( int j = i ; j < size ; j++ )
// array[ j + 1 ] = array[ j ] ;
// array[ i ] = key ;
int main() {
int a[ 100 ] ;
int size = 0 ;
int x ;
// 入力された値を登録していく繰り返し処理
while( scanf( "%d" , &x ) == 1 ) {
// x を追加する。
entry( a , &size , x ) ;
}
return 0 ;
}
これで判るように、昇順に並んだ配列にデータを追加する場合、途中にデータを入れる際にデータを後ろにずらす処理が発生する。
この例は、データを追加する場合であったが、不要となったデータを取り除く場合にも、データの場所の移動が必要である。
このことから、昇順に並べられた配列は、データの追加処理の発生頻度が少ない場合は2分探索法で効率が良いが、データの追加や削除が頻繁に発生する時はあまり効率が良くない。
順序が重要なデータ列で途中へのデータ挿入削除を高速化
例えば、アパート入居者に回覧板を回すことを考える。この中で、入居者が増えたり・減ったりした場合、どうすれば良いか考える。
以下の説明のような方法であれば、自分の所に回覧板が回ってきたら、次の入居者の部屋番号さえわかっていれば、スムーズに回覧板を回すことができる。
101 102 103 104 105 106 アパートの番号 [ 105 | 106 | -1 | 102 | 104 | 103 ] 回覧板を回す次の人の部屋番号 101号室の次は、105号室、 105号室の次は、104号室、 : 106号室の次は、103号室、 103号室の次は、おしまい(-1)
このように「次のデータの場所」という概念を使うと、データの順序を持って扱うことができる。これをプログラムにしてみよう。
struct LIST {
int data ; // 実際のデータ
int next ; // 次のデータの配列の添字
} ;
struct LIST array[] = {
/*0*/ { 11 , 2 } ,
/*1*/ { 67 , 3 } , // 末尾にデータ34を加える
/*2*/ { 23 , 4 } , // { 23 , 5 } ,
/*3*/ { 89 , -1 } , // 末尾データの目印
/*4*/ { 45 , 1 } ,
/*5*/ { 0 , 0 } , // { 34 , 4 } ,
} ;
int main() {
for( int idx = 0 ; idx >= 0 ; idx = array[ idx ].next ) {
printf( "%d\n" , array[ idx ].data ) ;
}
// 11,23,45,67,89,終
array[5].data = 34 ;
array[5].next = 4 ; // /*4*/ {45,1}
array[2].next = 5 ;
// O(1)で1件追加
for( int idx = 0 ; idx >= 0 ; idx = array[ idx ].next ) {
printf( "%d\n" , array[ idx ].data ) ;
}
// 11,23,[[34]],45,67,89,終
return 0 ;
}
この方法を取れば、途中にデータ入れたり、抜いたりする場合に、データの移動を伴わない。(O(N)の処理が発生しない)
しかし、配列をベースにしているため、配列の上限サイズを超えて格納することはできない。そこで、必要に応じてメモリを確保するテクニックを導入する。