3年の情報制御基礎の授業の一回目。この授業では、情報系以外の学生も受講することから、基礎的な共通的な話題を中心に説明を行う。
情報制御基礎のシラバス
情報制御基礎では、ここに上げたシラバスに沿って授業を行う。
基本的に、センサーから読み取ったデータを使って動く制御系システムを作る場合の基礎知識ということで、アナログ量・デジタル量の話から、移動平均やデータ差分といった数値処理や、そこで求まった値を制御に用いるための基礎的な話を行う。
コンピュータと組み込み系
最近では、コンピュータといっても様々な所で使われている。
- 科学技術計算用の大型コンピュータ(最近なら富岳や京が有名)や
- インターネットの処理を行うサーバ群
(必要に応じてサービスとして提供されるものはクラウドコンピューティングと呼ぶ)、 - デスクトップパソコン・ノートパソコン
- タブレットPCやスマートフォンのような端末、
- 電化製品の中に収まるようなワンチップコンピュータ
などがある。(3)のパソコンでもグラフィックス表示機能のために GPU(Graphics Processing Unit) を搭載したものは(ゲームでの3次元表示用)、高速計算に使われることも多い。

(5) ワンチップコンピュータ:PIC
身近で使われている情報制御という点では、(5)のような小型のコンピュータも多く、こういったものは組み込み型コンピュータとも呼ばれる。しかし、こういったコンピュータは、小さく機能も限られているので、
- 組み込み系では、扱える数値が整数で 8bit や 16bit といった精度しかなかったり、
- 実数を伴う複雑な計算をするには、処理時間がかかったりする
ため、注意が必要である。
この情報制御基礎の授業では、組み込み系のコンピュータでも数値を正しく扱うための知識や、こういった小さいコンピュータで制御を行うことを踏まえたプログラミングの基礎となる知識を中心に説明を行う。
2進数と10進数
コンピュータの中では、電圧が高い/低いといった状態で0と1の2通りの状態を表し、その 0/1 を組み合わせて、大きな数字を表す(2進数)。
練習として、2進数を10進数で表したり、10進数を2進数に直してみよう。
N進数を10進数に変換
N進数で “abcde” があったとする。(2進数で”10101)2“とか、10進数で”12345)10“とか)
この値は、以下のような式で表せる。
(例1)
(例2)
10進数をN進数に変換
N進数のは、前式を変形すると、以下のような式で表せることから、
値をNで割った余りを求めると、N進数の最下位桁eを取り出せる。
このため、10進数で与えられた35を2進数に変換するのであれば、35を2で次々と割った余りを、下の桁から書きならべれば2進数100011)2が得られる。
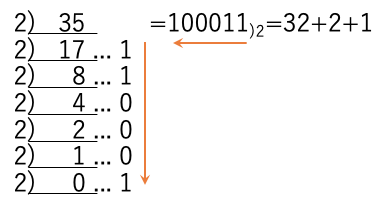
実数の場合
途中に小数点を含むN進数のab.cde)Nであれば、以下の値を意味する。
ここで、小数点以下だけを取り出した、0.cde)Nを考えると、
の値に、Nをかけると、次のように変形できる。
この式を見ると、小数部にNをかけると、整数部分に小数点以下1桁目が取り出せる。
このため、10進数で与えられた、0.625を2進数に変換するのであれば、0.625に次々と2をかけて、その整数部を上の桁から書きならべれば、2進数0.101)2が得られる。
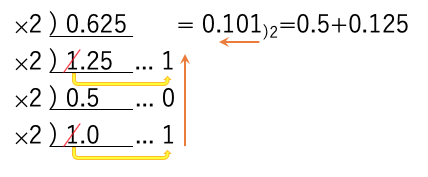
ただし、10進数で0.1という値で、上記の計算を行うと、延々と繰り返しが発生する。つまり、無限小数になるので注意せよ。
2の補数と負の数
コンピュータの中で引き算を行う場合には、2の補数がよく使われる。2の補数とは、2進数の0と1を入替えた結果(1の補数)に、1を加えた数である。

元の数に2の補数
を加えると(2進数が8bitの数であれば)、どのような数でも1,0000,0000という値になる。この先頭の9bit目が必ずはみ出し、この値を覚えないのであれば、元の数+2の補数=0とみなすことができる。このことから、2の補数= (-元の数) であり、負の数を扱うのに都合が良い。
練習問題
(1) 自分の誕生日で、整数部を誕生日の日、小数点以下を誕生日の月とした値について、2進数に変換せよ。(例えば、2月7日の場合は、”7.02″という小数点を含む10進数とする。)
変換の際には、上の説明の中にあるような計算手順を示すこと。また、その2進数を10進数に直し、元の値と同じか確認すること。(ただし、結果の2進数が無限小数になる場合最大7桁まで求めれば良い。同じ値か確認する際には無限少数の場合は近い値になるか確認すること)
(2) 自分の誕生日の日と、自分の学籍番号の下2桁の値を加えた値について、8bitの2進数で表わせ。(2月7日生まれの出席番号13番なら7+13=21)
その後、8bitの2進数として、2の補数を求めよ。また、元の数と2の補数を加えた値についても検証すること。
レポートの提出先は、こちらのリンクを参照(この中にレポート書式のひな型を置いてあります)
