2分探索木への追加とAVLと2分ヒープ

2024年11月
日	月	火	水	木	金	土
	1	2
3	4	5	6	7	8	9
10	11	12	13	14	15	16
17	18	19	20	21	22	23
24	25	26	27	28	29	30

2分探索木にデータを追加

前回の2分探索木では、基本的な説明ということで、木の生成では直接木構造を生成していた。しかし、本来であれば、扱うデータに応じて木を生成することが求められる。

Javaの場合

以下の Javaのプログラムの関数 entry( … ) では、再帰を使いながら、value を追加した木を返す関数で記述した。

import java.util.*;

class BTreeNode {
    int       data ;
    BTreeNode left ;
    BTreeNode right ;
    
    BTreeNode( int x , BTreeNode l , BTreeNode r ) {
        this.data  = x ;
        this.left  = l ;
        this.right = r ;
    }
}
public class Main {
    public static void print_tree( BTreeNode p ) {
        // 木構造をわかりやすくするために()をつけて表示
        if ( p != null ) {
            System.out.print( "(" ) ;
            print_tree( p.left ) ;
            System.out.print( p.data ) ;
            print_tree( p.right ) ;
            System.out.print( ")" ) ;
        }
    }
    public static BTreeNode entry( BTreeNode p , int value ) {
        if ( p == null ) {
            return new BTreeNode( value , null , null ) ;
        } else {
            if ( p.data == value )
                ; // 何もしない
            else if ( p.data > value )
                p.left = entry( p.left , value ) ;
            else
                p.right = entry( p.right , value ) ;
            return p ;
        }
    }
    public static void main(String[] args) throws Exception {
        BTreeNode top = null ;
        top = entry( top , 42 ) ;
        top = entry( top , 27 ) ;
        top = entry( top , 72 ) ;
        top = entry( top , 13 ) ;
        top = entry( top , 38 ) ;
        top = entry( top , 64 ) ;
        top = entry( top , 81 ) ;
        print_tree( top ) ; System.out.println() ;
    }
}
// 動作結果
// (((13)27(38))42((64)72(81)))

2分探索木へのデータの追加(Paiza.io)

しかしながらこのプログラムでは、以下のように小さい順序でデータを与えると、右に伸びる木が作られてしまう。

    // 不均一な木ができる場合
    public static void main(String[] args) throws Exception {
        BTreeNode top = null ;
        top = entry( top , 13 ) ;
        top = entry( top , 27 ) ;
        top = entry( top , 38 ) ;
        top = entry( top , 42 ) ;
        top = entry( top , 64 ) ;
        top = entry( top , 72 ) ;
        top = entry( top , 81 ) ;
        print_tree( top ) ; System.out.println() ;
    }
    // 動作結果
    // (13(27(38(42(64(72(81)))))))

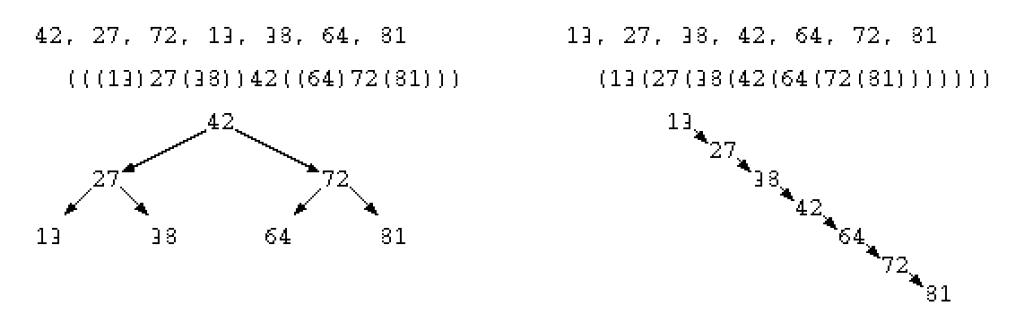
このような不均一な木が生成されてしまうと、本来であればデータ探索の処理時間は O( log N ) であるが、最悪の状態では O( N ) となってしまう。

AVL木

こういった偏った木が生成されてしまった時には、以下のような処理を加えると、不均一な状態を改善できる。

depth() 関数は与えられた木の深さを求める関数であり、左枝と右枝が大きく違う場所で木の右回転を行う rotate_right() を実行する。

public class Main {
    public static int depth( BTreeNode p ) { // 木の深さを求める
        if ( p == null ) {
            return 0 ;
        } else {
            int l = depth( p.left ) ;
            int r = depth( p.right ) ;
            if ( l > r )
                return 1 + l ;
            else
                return 1 + r ;
        }
    }
    public static BTreeNode rotate_right( BTreeNode p ) {
        BTreeNode q = p.left ;      //      p
        BTreeNode r = q.right ;     //    ／ ＼
        q.right = p ;               //   q
        p.left  = r ;               // ／ ＼
        return q ;                  //      r
    }
    public static void main(String[] args) throws Exception {
        BTreeNode top = null ;
        top = entry( top , 86 ) ;
        top = entry( top , 53 ) ;
        top = entry( top , 92 ) ;
        top = entry( top , 11 ) ;
        top = entry( top , 65 ) ;
        top = entry( top , 22 ) ;
        // 不均一な状態を確認
        print_tree( top ) ;
        System.out.println() ;
        System.out.println( "p.left=" + depth( top.left ) ) ;
        System.out.println( "p.right=" + depth( top.right ) ) ;
        // top の右回転を実行
        top = rotate_right( top ) ;
        // 改善された状態を確認
        print_tree( top ) ;
        System.out.println() ;
        System.out.println( "p.left=" + depth( top.left ) ) ;
        System.out.println( "p.right=" + depth( top.right ) ) ;
    }
}

AVL木と右回転(Paiza.io)

上記のプログラムでは、左枝が3段で右枝が1段であり不均一な状態となっている。

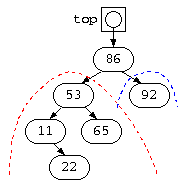
そこで、最上段の86の左枝を上に移動させるように枝の繋ぎ方を rotate_right() により変更している。実際には、繋ぎ変えを左回転させる処理も作る必要がある。

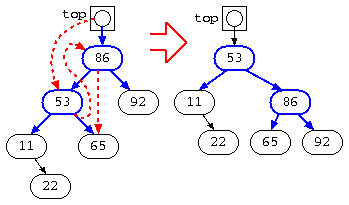このように、木の枝の深さが不均一な場所で、このような処理を加えて均一化を図った木構造は AVL 木と呼ぶ。

AVL木は、考案した Velski と Landis の名前が由来(Adelson-Velskii and Landis’ tree)

2分ヒープ(binary heap)

2分探索木では、１つのノードにつき2つのポインタを持ち、データ1件あたりのメモリの使用量が多い。通常の「配列の先頭から昇順にデータを並べる2分探索法」では、途中にデータを挿入する場合、データを後ろにずらす必要があるため、O(N)の処理時間を要する。

これらの問題の解決法の１つとして、2分ヒープがある。左右に均一に成長している2分探索木で、上から番号を以下の様に振ると、i番目のデータの左の枝は 2×i+1 番目、右の枝は 2×i+2 番目であることが判る。

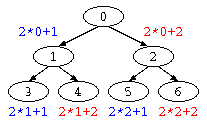
このような順序で配列にデータを保存する方法が2分ヒープである。この方式ならアルゴリズムの説明は省略するが、入れるべきノードの場所でのデータの入れ替えで実現できるため O( log( N ) )で挿入が可能となる。

import java.util.*;

public class Main {
    public static int find_heap( int[] array , int idx , int key ) {
        while( idx < array.length ) { if ( array[ idx ] == key ) return idx ; // 見つかった else if ( array[ idx ] > key )
                idx = idx*2 + 1 ;
            else
                idx = idx*2 + 2 ;
        }
        return -1 ; // 見つからなかった
    }
    public static void main(String[] args) throws Exception {
        int[] a = { 53 , 11 , 86 , 10 , 22 , 65 , 92 } ;
        System.out.println( find_heap( a , 0 , 22 ) ) ;
    }
}

2分ヒープ(Paiza.io)

レポート課題

以下のようなデータを扱う2分探索木のプログラムを作成せよ。以下の箇条書き番号の中から、(出席番号 % 3+1)のデータについてプログラムを作ること。

名前(name)と電話番号(phone)
名前(name)と誕生日(year,mon,day)
名前(name)とメールアドレス(mail)

プログラムは以下の機能を持つこと。

1行1件でデータを入力し、2分木に追加できること。
全データを昇順(or降順)で表示できること。
検索条件を入力し、目的のデータを探せること。

レポートでは、(a)プログラムリスト,(b)その説明,(c)動作検証結果,(d)考察を記載すること。

電子情報工学科

リンク集

検索・リンク