プログラミングコンテストの競技部門では、パズルのような組み合わせ問題が 出題されることが多い。また、課題部門や自由部門であっても、複数の条件の組み合わせの中から最良のものを選ぶといった処理も求められる。そこで、この予備実験では、きわめて単純なパズル問題(組み合わせ問題) のプログラムについて扱う。
組み合わせ問題の基礎
簡単な問題として「100未満の整数の値を3つ選び、その値を辺の長さとした場合、 直角三角形となるものをすべて表示する。」について考える。
一番簡単な方法は、以下となるであろう。
#include <stdio.h>
#include <math.h>
#include <time.h>
// 整数比の直角三角形の一覧を求める。
void integer_triangle( int n ) {
for( int a = 1 ; a < n ; a++ ) {
for( int b = 1 ; b < n ; b++ ) {
// 一番ダサい方法
for( int c = 1 ; c < n ; c++ ) {
if ( a*a + b*b == c*c ) {
printf( "%d %d %d\n" , a , b , c ) ;
}
}
}
}
}
int main() {
integer_triangle( 100 ) ;
return 0 ;
}
しかしこのプログラムの欠点としては、100×100×100回のループで無駄な処理が多い。
4EIの情報構造論で説明するネタだけど、こういうアルゴリズムは、O(N3) のアルゴリズムという。
ループ回数を減らすだけなら、最も内側の処理を、計算で整数値か確認すればいい。
O(N2) のアルゴリズム
void integer_triangle( int n ) {
for( int a = 1 ; a < n ; a++ ) {
for( int b = 1 ; b < n ; b++ ) {
// ココも改良できるよね?
int d = a*a + b*b ;
int c = (int)sqrt( d ) ;
// 斜辺Cの整数値を求め、改めて確認する。
if ( c*c == d ) {
printf( "%d %d %d\n" , a , b , c ) ;
}
}
}
}
(1) 計算誤差の問題を考えてみよう。
たとえば、3:4:5の直角三角形で、3*3+4*4 = 25 だが、sqrt(25)は実数で計算するから、 計算誤差で4.99999で求まったらどうなるだろうか?
1~100までの数値で、”int c = sqrt( (double)(i*i) ) ;” を計算してみて、 異なる値が求まることはあるか? 多少の計算誤差があっても正しく処理が行われるにはどうすればいいか、考えてみよう。
(2) 無駄な答えについて考えてみよう。
このプログラムの答えでは、簡単な整数比の答えの「整数倍の答え」も表示されてしまう。 たとえば、(3:4:5)の答えのほかに、(6:8:10)も表示される。 こういった答えを表示しないようにするにはどうすればよいか?
また、この2つのプログラムの処理時間を実際に比べてみる。
#include <stdio.h>
#include <time.h>
int main() {
time_t start , end ;
// time() 関数は、秒数しか求まらないので、
// あえて処理を1000回繰り返し、数秒かかる処理にする。
start = time( NULL ) ;
for( int i = 0 ; i < 1000 ; i++ ) {
// ただし、関数内のprintfをコメントアウトしておくこと
integer_triangle( 100 ) ;
}
end = time( NULL ) ;
printf( "%lf\n" , difftime( end , start ) ) ;
return 0 ;
}
再帰プログラミング
組み合わせ問題では、forループの多重の入れ子で問題を解けない場合が多い。 (書けないことはないけど無駄なループで処理が遅くなるか、入れ子段数が可変にできない。)
こういった場合には、再帰プログラミングがよく利用される。 もっとも簡単な再帰の例として、階乗のプログラムを考える。 通常であれば、以下のような for ループで記述することになるだろう。
// 階乗の計算
int fact( int x )
{ // ループ
int f = 1 ;
for( int i = 2 ; i <= x ; i++ )
f = f * i ;
return f ;
}
再帰呼び出しでは、関数の処理の中に、自分自身の関数呼び出しが含まれる。 また、無限に自分自身を呼び出したら処理が止まらないので、 問題を一つ小さくして、これ以上小さくできないときは処理を止めるように記述する。
int fact( int x )
{ // 再帰呼び出し
if ( x <= 1 )
return 1 ;
else
return x * fact( x - 1 ) ;
}
ここ以降は、指定長さを指定辺の組み合わせで作る課題と、後に述べるFlood-fill 課題の選択とする。
指定長を指定辺の組み合わせで作る(テーマ1)
再帰を使った簡単なパズル問題として、以下のプログラムを作成したい。
配列の中に、複数の辺の長さが入っている。これを組み合わせて指定した長さを作れ。 使用する辺はできるだけ少ない方がよい。
int a[] = { 4 , 5 , 2 , 1 , 3 , 7 } ;
(例) 辺の長さ10を作るには、(5,4,1)とか(7,3)などが考えられる。
これは、ナップサック問題の基本問題で、容量の決まったナップサックに最大量入れる組合せを求めるのと同じである。
このプログラムを解くには…
10 を [4,5,2,1,3,7] で作るには... (0) 6=10-4 を [4|5,2,1,3,7]で作る。 (1) 5=10-5 を [5|4,2,1,3,7]で作る。 (2) 8=10-2 を [2|5,4,1,3,7]で作る。 (3) 9=10-1 を [1|5,2,4,3,7]で作る。 (4) 7=10-3 を [3|5,2,1,4,7]で作る。 (5) 3=10-7 を [7|5,2,1,3,4]で作る。
そこで、ここまでの考えを、以下のようなプログラムで記述してみる。
# まだ再起呼び出しにはしていない。
// 指定されたデータを入れ替える。
void swap( int*a , int*b )
{ int x = *a ;
*a = *b ;
*b = x ;
}
void check( int array[] , int size , int len , int n )
{
// array[] 配列
// size 配列サイズ
// len 作りたい長さ
// n 使った個数
for( int i = n ; i < size ; i++ ) {
// i番目を先頭に...
swap( &array[ n ] , &array[ i ] ) ;
printf( "check( array , %d , %d , %d )\n" ,
size , len - array[ n ] , n+1 ) ;
// 最初のswapでの変更を元に戻す。
swap( &array[ i ] , &array[ n ] ) ;
}
}
int main() {
int a[] = { 4 , 5 , 2 , 1 , 3 , 7 } ;
check( a , 6 , 10 , 0 ) ;
}
(1) これを再帰呼び出しにしてみよう。どう書けばいい?
void check( int array[] , int size , int len , int n )
{
// array[] 配列
// size 配列サイズ
// len 作りたい長さ
// n 使った個数
if ( len < 0 ) {
// 指定した丁度の長さを作れなかった。
;
} else if ( len == 0 ) {
// 指定した長さを作れたので答えを表示。
for( int i = 0 ; i < n ; i++ ) {
printf( "%d " , array[ i ] ) ;
}
printf( "\n" ) ;
} else {
// 問題を一つ小さくして再帰。
for( int i = n ; i < size ; i++ ) {
swap( &array[ n ] , &array[ i ] ) ;
printf( "check( array , %d , %d , %d )\n" ,
size , len - array[ n ] , n+1 ) ;
check( array , size , len - array[ n ] , n + 1 ) ;
swap( &array[ i ] , &array[ n ] ) ;
}
}
}
(2) 少ない組み合わせの方がポイントが高い場合には、プログラムをどう変更する?
(3) 答えが1つだけで良い場合は、プログラムをどう変更する?
(4) このプログラムでは、冗長な答えがあるか?ないか?検討せよ。
(5) 前設問の整数比直角三角形のプログラムで、冗長な答えを削除するプログラムを作成せよ。
# レポートでは、(2),(3),(4)を検討した結果を実験すること。(5)までチャレンジした人は(2),(3),(4)の説明は簡単に記載するだけで良い。
別解
この問題の解き方には、もっとシンプルな書き方がある。2進数の各bitを、j番目の長さを使うか使わないかを表すこととする。
例えば、j=1番目,3番目を使うというのを、000101)2=5で表すこととする。すべての長さを使うのであれば、111111)2=63 で表す。この2進数を1から63まで変化させれば、すべての組み合わせを試すことになる。
#include <stdio.h>
#define sizeofarray(A) (sizeof(A)/sizeof(A[0]))
int obj_len = 10 ;
int a[] = { 4 , 5 , 2 , 1 , 3 , 7 } ;
int main() {
int l_max = 1 << sizeofarray( a ) ;
for( int i = 1 ; i < l_max ; i++ ) {
// i は a[j]を使うか使わないかを表す2進数
// i = 5 の場合
// 5 = 0,0,0,1,0,1
// a[] 7,3,1,2,5,4
// ^ ^ = 長さは6
int sum = 0 ;
for( int j = 0 ; j < sizeofarray( a ) ; j++ ) {
// iの2進数の各bitに対応する長さを加算
if ( (i & (1 << j)) != 0 )
sum += a[ j ] ;
}
// 目的の長さを作れたので答えを表示
if ( sum == obj_len ) {
printf( "0x%x : " , i ) ;
for( int j = 0 ; j < sizeofarray( a ) ; j++ ) {
if ( (i & (1 << j)) != 0 ) {
printf( "%d " , a[ j ] ) ;
}
}
printf( "\n" ) ;
}
}
return 0 ;
}
このプログラムは再帰呼び出しを含まないので、プログラムの挙動も解りやすい。しかし、j番目を使うか使わないのか…という2つの状態しかない組み合わせ問題でしか使えない。R3年度の競技部門のパズルように、絵のピースの↑,→,↓,←,回転右,回転左という6状態の場合は、使えない。
Flood fill アルゴリズム
再帰を使う他の事例として、図形の塗りつぶし問題で示す。(Wikipedia Flood-fill参照)
以下の image のような2次元配列が与えられたら、指定座標(x,y)を中心に周囲を塗りつぶす処理を作成せよ。
include <stdio.h>
// *は壁 SPCは白 この領域の指定位置を#で塗りつぶす。
char image1[10][10] = { // (4,4)始点で塗りつぶし後
"*********" , // *********
"* * *" , // * *###*
"* * *" , // * *###*
"* * *" , // * *####*
"*** ***" , // ***###***
"* * *" , // *####* *
"* * *" , // *###* *
"* * *" , // *###* *
"*********" , // *********
} ;
char image2[10][10] = { // 応用問題用の画像例
"*********" , // * のような隙間は通り抜けられる
"* * *" , // * ようにするにはどうすればいい?
"* ** *" , // **
"* ** *" , // ** これは通り抜けられない
"*** ***" , // **
"* * *" ,
"* * *" ,
"* * *" ,
"*********" ,
} ;
// 盤面を表示
void print_image( char image[10][10] ) {
for( int y = 0 ; y < 9 ; y++ ) {
for( int x = 0 ; x < 9 ; x++ ) {
printf( "%c" , image[y][x] ) ;
}
printf( "\n" ) ;
}
}
// 再帰呼び出しを使った flud_fill アルゴリズム
void flood_fill( char image[10][10] , int x , int y , char fill ) {
// image: 塗りつぶす画像
// x,y: 塗りつぶす場所
// fill: 書き込む文字
// 指定座標が空白なら
if ( image[y][x] == ' ' ) {
// その座標を埋める
image[y][x] = fill ;
//////////////////////////////////////
// ここに周囲をflud_fillする処理を書く //
//////////////////////////////////////
}
}
int main() {
print_image( image1 ) ;
flood_fill( image1 , 4 , 4 , '#' ) ;
print_image( image1 ) ;
return 0 ;
}
応用問題
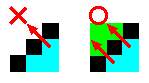
Wikipediaのflood-fill のプログラムの説明のアルゴリズムでは、左図黒のような斜めに並んだブロックは、境界として通り抜けられないようにつくられている。
そこで、斜めに並んだブロックは通り抜けられるルールとした場合のプログラムを記述せよ。
レポート提出
レポートでは、指定長を辺の組み合わせで作るテーマか、Flood-fill のテーマのいずれかにて、以下の内容をまとめてレポートとして提出すること。
-
- レポートの説明(自分の選んだテーマと自分なりの説明)
- プログラムリスト
- 動作確認の結果