AVLと2分ヒープ
前回、2分探索木へのデータ追加の説明と、演習課題を行っていたが、演習時間としては短いので、今日も前半講義で残り時間は演習とする。
2分探索木へのデータ追加と不均一な木の成長
先週の講義で説明していた、entry() では、データを追加すべき末端を探し、追加する処理であった。
しかし、前回のプログラムで、以下のような順序でデータを与えたら、どのような木が出来上がるであろうか?
- 86, 53, 11 – 降順のデータ
- 12, 24, 42 – 昇順のデータ
この順序でデータが与えられると、以下のような木が出来上がってしまう。このような木では、データを探しても1回の比較でもデータ件数が1つ減るだけで、O(N)となってしまう。通常のデタラメな順序でデータが与えられれば、木はほぼ左右均等に成長するはずである。
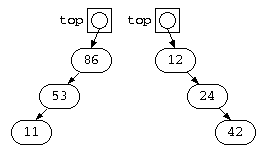
AVL木
このような、不均一な木が出来上がっても、ポインタの繋ぎ変えで検索回数を改善できる。例えば、以下のような木では、赤の左側に偏っている。
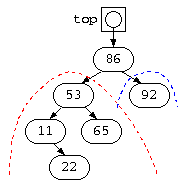
このような場合でも、最初、青の状態であっても、不均一な部分で赤のようなポインタの繋ぎ変えを行えば、木の段数を均一に近づけることができる。この例では、11,65,92の木が、右回転して 11 の木の位置が上がっている。(右回転)
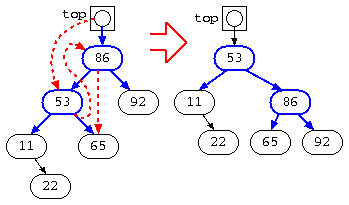
この様に、左右の枝の大きさが不均一な場所を見つけ、右回転や左回転を行う処理を繰り返すことで、段数が均一な2分探索木に修正ができる。この様な処理でバランスの良い木に修正された木は、AVL木と呼ばれる。
理解確認
- 木の根からの段数を求める関数 tree_depth() を作成せよ。
例えば、上のAVL木の説明の図であれば、4段なので4を返すこと。
// 木の段数を数える関数
_____ tree_depth( _______________ p ) {
if ( p == NULL ) {
return _____ ;
} else {
int d_L = ______________ ;
int d_R = ______________ ;
if ( d_L > d_R )
return _____ ;
else
return _____ :
}
}
// pをつなぎ替え上部を返り値で返す。
struct Tree*rot_right( struct Tree* p ) {
struct Tree* pl = p->left ;
struct Tree* pr = pl->right ;
pl->right = p ;
p->left = = pr ;
return pl ;
}
int main() {
printf( "%d¥n" , tree_depth( top ) ) ;
top = rot_right( top ) ;
return 0 ;
}
2分ヒープ(binary heap)
2分探索木では、1つのノードにつき2つのポインタを持ち、データ1件あたりのメモリの使用量が多い。通常の「配列の先頭から昇順にデータを並べる2分探索法」では、途中にデータを挿入する場合、データを後ろにずらす必要があるため、O(N)の処理時間を要する。
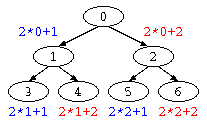
これらの問題の解決法の1つとして、2分ヒープがある。左右に均一に成長している2分探索木で、上から番号を以下の様に振ると、i番目のデータの左の枝は 2×i+1 番目、右の枝は 2×i+2 番目であることが判る。
このような順序で配列にデータを保存する方法が2分ヒープである。この方式ならアルゴリズムの説明は省略するが、O(log(N))で挿入が可能となる。
int a[ 7 ] = { 53 , 11 , 86 , 10 , 22 , 65 , 92 } ;
// 2分ヒープを表示
void print_heap( int array[] , int idx , int size ) {
if ( idx < size ) {
// 左の枝を表示
print_heap( array , 2*idx + 1 , size ) ;
// 真ん中の枝を表示
printf( "%d " , array[ idx ] ) ;
// 右の枝を表示
print_heap( array , 2*idx + 2 , size ) ;
}
}
// 2分ヒープから key を検索
int find_heap( int array[] , int idx , int size , int key ) {
while( idx < size ) {
if ( array[ idx ] == key )
return idx ; // 見つかったら配列の番号を返す
else if ( array[ idx ] _____ key ) // 何が入るか考えよう
idx = ________________ ;
else
idx = ________________ ;
}
return -1 ; // 見つからなかったら、-1 を返す
}
int main() {
print_heap( a , 0 , 7 ) ;
if ( find_heap( a , 0 , 7 , 65 ) >= 0 )
printf( "Find!!¥n" ) ;
return 0 ;
}