集合とリスト処理
リスト構造は、必要に応じてメモリを確保するデータ構造であり、データ件数に依存しないプログラム が記述できる。その応用として、集合処理を考えてみる。集合処理の記述には、2進数を使った方式やリストを用いた方法が一般的である。以下にその処理について示す。
bit演算子
2進数を用いた集合処理を説明する前に、2進数を使った計算に必要なbit演算子について復習してみる。
| bit演算子 | 計算の意味 | 関連知識 |
|---|---|---|
| & bit AND | 3 & 5 0011)2 & 0101)2= 0001)2 |
論理積演算子 if ( a == 1 && b == 2 ) … |
| | bit OR | 3 | 5 0011)2 | 0101)2= 0111)2 |
論理和演算子 if ( a == 1 || b == 2 ) … |
| ~ bit NOT | ~5 ~ 00..00,0101)2= 11..11,1010)2 |
論理否定演算子 if ( !a == 1 ) … |
| ^ bit EXOR | 3 ^ 5 0011)2 ^ 0101)2= 0110)2 |
|
| << bit 左シフト | 3 << 2 0011)2 << 2 = 001100)2 |
x << y は x * 2y と同じ |
| >> bit 右シフト | 12 >> 2 1100)2 >> 2 = 11)2 |
x >> y は x / 2y と同じ |
#include <stdio.h>
int main() {
// bit演算子と論理演算子
printf( "%d¥n" , 12 & 5 ) ; // 1100 & 0101 = 0100 よって 4が表示される
printf( "%d¥n" , 12 && 0 ) ; // 0が表示 論理演算子とbit演算子の違い
printf( "%d¥n" , 12 | 5 ) ; // 1100 | 0101 = 1101 よって 13が表示される
printf( "%d¥n" , 12 || 0 ) ; // 1が表示
// シフト演算子
printf( "%d¥n" , 3 << 2 ) ; // 12が表示
printf( "%d¥n" , 12 >> 2 ) ; // 3が表示
// おまけ
printf( "%d¥n" , ~(unsigned)12 + 1 ) ; // 2の補数(NOT 12 + 1) = -12
return 0 ;
}
2進数を用いた集合計算
リストによる集合の前に、もっと簡単な集合処理を考える。
最も簡単な方法は、要素に含まれる=1 か 含まれない=0 を配列に覚える方法であろう。数字Nが集合に含まれる場合は、配列[N]に1を覚えるものとする。この方法で積集合などを記述した例を以下に示す。ただし、自分で考える練習として穴埋めを含むので注意。
しかし、上述のプログラムでは、要素に含まれる/含まれないという1bitの情報を、整数型で保存しているためメモリの無駄である。
データ件数の上限が少ない場合には、「2進数の列」の各ビットを集合の各要素に対応づけし、要素の有無を0/1で表現する。この方法を用いるとC言語のビット演算命令で 和集合、積集合を計算できるので、処理が極めて簡単になる。
2進数を用いた集合計算
扱うデータ件数が少ない場合には、「2進数の列」の各ビットを集合の各要素に対応づけし、要素の有無を0/1で表現する。この方法を用いるとC言語のビット演算命令で 和集合、積集合を計算できるので、処理が極めて簡単になる。
以下のプログラムは、0〜31の数字を2進数の各ビットに対応付けし、 ba = {1,2,3} , bb = {2,4,6} , bc= {4,6,9} を要素として持つ集合で、ba ∩ bb , bb ∩ bc , ba ∪ bc の計算を行う例である。
// 符号なし整数を uint_t とする。
typedef unsigned int uint_t ;
// uint_tのbit数
#define UINT_BITS (sizeof( uint_t ) * 8)
// 集合の内容を表示
void bit_print( uint_t x ) {
for( int i = 0 ; i < UINT_BITS ; i++ )
if ( (x & (1 << i)) != 0 )
printf( "%d " , i ) ;
printf( "\n" ) ;
}
void main() { // 98,7654,3210
// ba = {1,2,3} = 00,0000,1110
uint_t ba = (1<<1) | (1<<2) | (1<<3) ;
// bb = {2,4,6} = 00,0101,0100
uint_t bb = (1<<2) | (1<<4) | (1<<6) ;
// bc = {4,6,9} = 10,0101,0000
uint_t bc = (1<<4) | (1<<6) | (1<<9) ;
// 集合積(bit AND)
bit_print( ba & bb ) ; // ba ∩ bb = {2}
bit_print( bb & bc ) ; // bb ∩ bc = {4,6}
// 集合和(bit OR)
bit_print( ba | bc ) ; // ba ∪ bc = {1,2,3,4,6,9}
}
有名なものとして、エラトステネスのふるいによる素数計算を2進数を用いて記述してみる。このアルゴリズムでは、各bitを整数に対応付けし、素数で無いと判断した2進数の各桁に1の目印をつけていく方式である。
uint_t prime = 0 ; // 初期値=すべての数は素数とする。
void filter() {
// 倍数に非素数の目印をつける
for( int i = 2 ; i < UINT_BITS ; i++ ) {
if ( (prime & (1 << i)) == 0 ) {
// iの倍数には、非素数の目印(1)をつける
for( int j = 2*i ; j < UINT_BITS ; j += i )
prime |= (1 << j) ;
}
}
// 非素数の目印の無い値を出力
for( int i = 2 ; i < UINT_BITS ; i++ ) {
// 目印のついていない数は素数
if ( (prime & (1 << i)) == 0 )
printf( "%d\n" , i ) ;
}
}
リスト処理による積集合
前述の方法は、リストに含まれる/含まれないを、2進数の0/1で表現する方式である。しかし、2進数であれば、unsigned int で 32要素、unsigned long long int で 64 要素が上限となってしまう。 (32bitコンピュータ,gccの場合)
しかし、リスト構造であれば、リストの要素として扱うことで、要素件数は自由に扱える。また、今までの授業で説明してきた cons() などを使って表現すれば、簡単なプログラムでリストの処理が記述できる。
// 先週までに説明してきたリスト構造と補助関数
struct List {
int data ;
struct List* next ;
} ;
struct List* cons( int x , struct List* n ) {
struct List* ans ;
ans = (struct List*)malloc( sizeof( struct List ) ) ;
if ( ans != NULL ) {
ans->data = x ;
ans->next = n ;
}
return ans ;
}
void print( struct List* p ) {
for( ; p != NULL ; p = p->next ) {
printf( "%d " , p->data ) ;
}
printf( "\n" ) ;
}
int find( struct List* p , int key ) {
for( ; p != NULL ; p = p->next )
if ( p->data == key )
return 1 ;
return 0 ;
}
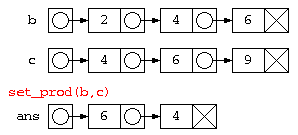
例えば、積集合(a ∩ b)を求めるのであれば、リストa の各要素が、リストb の中に含まれるか find 関数でチェックし、 両方に含まれたものだけを、ans に加えていく…という考えでプログラムを作ると以下のようになる。
// 集合積の計算
struct List* set_prod( struct List* a , struct List* b ) {
struct List* ans = NULL ;
for( ; a != NULL ; a = a->next ) {
// aの要素がbにも含まれていたら、ansに加える
if ( find( b , a->data ) )
ans = cons( a->data , ans ) ;
}
return ans ;
}
void main() {
struct List* a = cons( 1, cons( 2, cons( 3, NULL ) ) ) ;
struct List* b = cons( 2, cons( 4, cons( 6, NULL ) ) ) ;
struct List* c = cons( 4, cons( 6, cons( 9, NULL ) ) ) ;
print( set_prod( a , b ) ) ;
print( set_prod( b , c ) ) ;
}
例題として、和集合、差集合などを考えてみよう。
リストの共有と削除の問題
リスト処理では、mallocを使うが、メモリリークをさせないためには、使用後のリストの廃棄は重要である。リストの全要素を捨てる処理であれば、以下のようになるであろう。
void list_free( struct List* p ) {
while( p != NULL ) {
struct List* d = p ;
p = p->next ;
free( d ) ; // 順序に注意
}
}
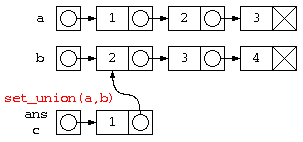
一方、前説明の和集合(a ∪ b)のプログラムを以下のように作った場合、list_freeの処理は問題となる。
// 集合和
struct List* set_union( struct List*a, struct List*b ) {
struct List* ans = b ;
for( ; a != NULL ; a = a->next )
if ( !find( b , a->data ) )
ans = cons( a->data , ans ) ;
return ans ;
}
void main() {
struct List*a = cons( 1, cons( 2, cons( 3, NULL ) ) ) ;
struct List*b = cons( 2, cons( 3, cons( 4, NULL ) ) ) ;
struct List*c = set_union( a , b ) ;
// a,b,cを使った処理
// 処理が終わったので、a,b,cを捨てる
list_free( a ) ;
list_free( b ) ;
list_free( c ) ;
// c = { 1 , (bのリスト) }
// (b)の部分は先のlist_free(b)で解放済み
}
このような、リストb,リストcで共有されている部分があると、データの廃棄処理をどのように記述すべきなのか、問題となる。
これらの解決方法としては、(1) set_union() の最初で、ans=b となっている部分を別にコピーしておく、(2) 参照カウンタ法を用いる、(3) ガベージコレクタのある言語を用いる…などがある。(2),(3)は後期授業で改めて解説を行う。
// 同じ要素を含む、新しいリストを作る struct List* copy( struct List*p ) { struct List*ans = NULL ; for( ; p != NULL ; p = p->next ) ans = cons( p->data , ans ) ; return ans ; } struct List* set_union( struct List*a, struct List* b ) { struct List* ans = copy( b ) ; // この後は自分で考えよう。 }
理解確認
- 2進数を用いた集合処理は、どのように行うか?
- リスト構造を用いた集合処理は、どのように行うか?
- 積集合(A ∩ B)、和集合(A ∪ B)、差集合(A – B) の処理を記述せよ。