フローチャートと数値型
学際科目の情報制御基礎において、プログラムの基本としてフローチャートと基本的な処理を説明し、数値型の注意点を説明。
フローチャートの基本
プログラムの処理の順序を理解するには、初心者であればフローチャート(流れ図)を使う。
処理の1つ1つを箱で表し、流れを箱の間の矢印で示すことでアルゴリズム(プログラムの考え方)や処理順序を表現する。処理単位の箱は、命令の種類によって箱の書き方が決まっている。
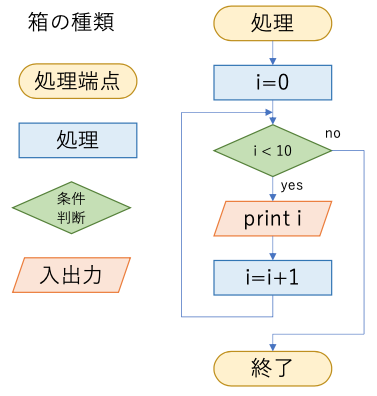 上図右側のフローチャートの例では、以下の説明のように実行され、0,1,2,…,9 が表示され、最終的に変数 i が10以上になり処理を停止する。
上図右側のフローチャートの例では、以下の説明のように実行され、0,1,2,…,9 が表示され、最終的に変数 i が10以上になり処理を停止する。
(1) 変数 i に 0 を保存
(2) 変数 i は10未満なら(3)、10以上なら終了
(3) 変数 i を表示
(4) i = i + 1 右辺の計算結果を、左辺に代入。iが0から1に変化
(5) 処理(2)から繰り返し。
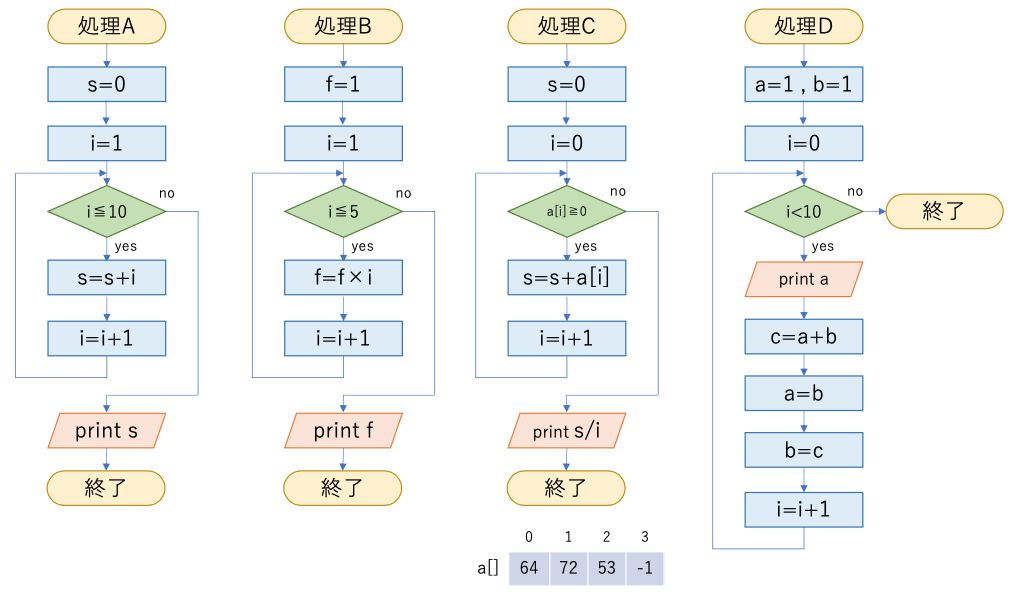
練習問題1
以下のフローチャートの処理A,処理B,処理C,処理Dの実行結果を答えよ。
- 電気電子工学科,電子情報工学科の学生は、出席番号が偶数は処理C,奇数は処理Dについて回答せよ。
- それ以外の学科の学生は、出席番号が偶数は処理A,奇数は処理Bの結果について回答せよ。
情報量の単位
データを覚える最小単位は、0と1の2通りで表される1bit (ビット)と呼ぶ。単位として書く場合には b で表す。さらに、その1bitを8個組み合わせると、256通りの情報を保存できる。256通りあれば一般的な英数字などの記号を1文字保存する入れ物として便利であり、この単位を 1byte (バイト) と呼ぶ。単位として書く場合には B で表す。
通信関係の人は8bit=1byteを1オクテットと呼ぶことも多い。日本語を表現するには、かなや漢字を使うため16bit = 2byte = 1word(ワード) で表現することが多い。(ただしワードは32bitを意味することもあるので要注意, double word=32bit, quad word=64bit という呼び方もある。)
物理では単位が大きくなると、103=kキロ,106=Mメガ,109=Gギガ,1012=Tテラ を使うが、コンピュータの世界では、103≒210=1024 なので、1kB(キロバイト)というと1024Bを意味することが多い。明確に区別する時は、1024B(バイト)=1KiB(キビバイト), 10242B=1MiB, 10243B=1GiB などと記載する。
2進数,8進数,16進数
プログラムの中で整数値を覚える場合は、2進数の複数桁で記憶する。例えば、2進数3桁(3bit)であれば、000, 001, 010, 011, 100, 101, 110, 111 で、10進数であれば 0~7 の8通りの値が扱える。(8進数)
2進数4桁(4bit)であれば、0000, 0001, 0010, 0011, 0100, 0101, 0110, 0111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111 の16通りを表現できる(16進数)。これを1桁で表現するために、0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F を使って表現する。
例 8進数 16進数
0123 0x123 ※C言語では、
+ 026 + 0xEA 8進数を表す場合、先頭に0をつけて表す。
-------- -------- 16進数を表す場合、先頭に0xをつけて表す。
0151 0x20D
整数型と扱える値の範囲
コンピュータの開発が進むにつれ計算の単位となるデータ幅は、8bit, 16bit, 32bit, 64bit と増えていった。整数型データには、正の値しか覚えられない符号無し整数と、2の補数で負の数を覚える符号付き整数に分けられる。
プログラムを作るためのC言語では、それぞれ 8bitの文字型(char)、16bitの short int型、32bitの int 型、64bitの long int 型(※C言語では long int で宣言すると32bitの場合も多いので要注意)がある。
| 精度 | 符号あり | 符号なし |
| 8bit(1byte) | char (int8_t) | unsigned char (uint8_t) |
| 16bit(2byte) | short int (int16_t) | unsigned short int (uint16_t) |
| 32bit(4byte) | int (int32_t) | unsigned int (uint32_t) |
| 64bit(8byte) | long int※ (int64_t) | unsigned long int※ (uint64_t) |
符号付きのデータは、負の数は2の補数によって保存され、2進数の最上位bit(符号ビット)は負の数で1、正の数であれば0となる。
整数型で扱える数
(例) 符号なしの1byte(8bit)であれば、いくつの数を扱えるであろうか?
符号なしの N bit の整数であれば2N通りの値を表現でき、0~(2N-1) までの値が扱える。
| bit数 | 型 | 符号なし(unsigned) | |
| 8 | unsigned char | 0~28-1 | 0~255 |
| 16 | unsigned short int | 0~216-1 | 0~65535 |
| 32 | unsigned int | 0~232-1 | 0~4294967295 |
符号付きの N bit の整数であれば、最上位ビットが符号に使われるので、正の数なら残りの(N-1)bitで扱うため 0〜2N-1-1を表現できる。負の数は2N-1通りを表現できるので、N bit の符号つき整数は、-2N-1 〜0〜 2N-1-1の範囲の値を覚えられる。
| bit数 | 型 | 符号あり(signed) | |
| 8 | char | -27~0~27-1 | -128~127 |
| 16 | short int | -215~0~215-1 | -32768~32767 |
| 32 | int | -231~0~231-1 | -2147483648~2147483647 |
2の冪乗の概算
プログラムを作る場合、2の冪乗がだいたいどの位の値なのか知りたいことが多い。この場合の計算方法として、2つの方法を紹介する。
- 232 = (210)3 × 22 = 10243 × 4 ≒ 4,000,000,000
- 232をN桁10進数で表すとすれば
なので、両辺のlog10を求める。
(つまり、bit数に0.3をかければ10進数の桁数が求まる。)
数値の範囲の問題で動かないプログラム
この話だけだと、扱える数値の上限について実感がわかないかもしれないので、以下のプログラムをみてみよう。(C言語の詳細は説明していないので、問題点がイメージできるだけでいい。)
組み込み系のコンピュータでは、int 型で宣言される変数でも、16bitの場合もある。以下のプログラムは期待した値が計算できない例である。以下の例では、16bit int型として short int で示す。
// ✳️コード1
#include <stdio.h>
#include <math.h>
int main() { // 原点から座標(x,y)までの距離を求める
short int x = 200 ;
short int y = 200 ;
short int r2 = x*x + y*y ; // (x,y)までの距離の2乗
short int r = sqrt( r2 ) ; // sqrt() 平方根
printf( "%d\n" , r ) ; // 何が求まるか?
return 0 ; // (例) 282ではなく、120が表示された。
}
コンピュータで一定時間かかる処理を考えてみる。
// コード2.1 // 1 [msec] かかる処理が以下のように書いてあったとする。 short int i ; for( i = 0 ; i < 1000 ; i++ ) NOP() ; // NOP() = 約1μsecかかる処理とする。 // ✳️コード2.2 // 0.5 [sec]かかる処理を以下のようにかいた。 short int i ; for( i = 0 ; i < 500000 ; i++ ) NOP() ; // でもこの処理は16bitコンピュータでは、1μsecもかからずに終了する。なぜか?
上記の例は、性能の低い16bit コンピュータの問題で、最近は32bit 整数型のコンピュータが普通だし、特に問題ないと思うかもしれない。でも、32bit でも扱える数の範囲で動かなくなるプログラムを示す。
OS(unix) では、1970年1月1日からの経過秒数で時間(unix時間)を扱う。ここで、以下のプログラムは、正しい値が計算できない有名な例である。(2004年1月11日にATMが動かなくなるトラブルの原因だった)
// ✳️コード3.1 int t1 = 1554735600 ; // 2019年4月09日,00:00 int t2 = 1555340400 ; // 2019年4月16日,00:00 // この2日の真ん中の日を求める。 // t1 | t2 // |--------+--------| // | t_mid | // 以下のプログラムは、正しい 2019年4月12日12:00 が求まらない。なぜか? int t_mid = (t1 + t2) / 2; // (例) 1951年03月25日 08:45 になった。 // コード3.2 // 以下のプログラムは正しく動く。 time_t 型(時間処理用の64bit整数) time_t t1 = 1554735600 ; // 2019年4月09日,00:00 time_t t2 = 1555340400 ; // 2019年4月16日,00:00 // time_t型が32bitであったとしても桁溢れない式 time_t t_mid = t1 + (t2 - t1) / 2 ;
練習問題2
以下の整数の範囲を具体的な値で答えよ。
出席番号・自分の誕生日(の日にち)に合わせて該当する2問について答えること。
- 7bitの符号なし整数で扱える数値の範囲 (出席番号が偶数)
- 12bitの符号あり整数で扱える数値の範囲 (出席番号が奇数)
- 20bitの符号なし整数で扱える数値の範囲 (誕生日の日づけが偶数)
- 24bitの符号あり整数で扱える数値の範囲 (誕生日の日づけが奇数)
練習問題3
先に示した数値の範囲が原因で動かないプログラム(コード1,コード2.2,コード3.1)の中から1つを選んで、計算結果が正しく求まらない原因を、具体的な値を示しながら説明せよ。
練習問題1,練習問題2,練習問題3について、レポートとして提出せよ。