D/A・A/D変換回路と誤差
小型コンピュータを使った制御では、外部回路に指定した電圧を出力(D/A変換)したり、外部の電圧を入力(A/D変換)したりすることが多い。以下にその為の回路と動作について説明する。
D/A変換回路
ラダー抵抗回路によるD/A変換の仕組みを引用
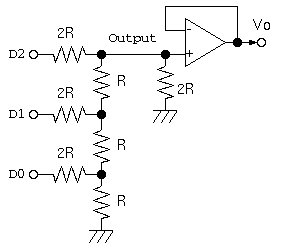
このような回路で、D0,D1,D2 は、デジタル値の0=0[V] , 1=5[V] であった場合、Output 部分の電圧は、(D0,D1,D2)の値が、(0,0,0),(0,0,1),…(1,1,1)と変化するにつれ、5/8[V]づつ増え、(1,1,1)で 5*(7/8)=4.4[V]に近づいていく。Output が出力によって電圧が変化しないように、アンプ回路を通す。
DCモータをアナログ量で制御しないこと
このように、電圧をコンピュータから制御するようになると、ロボットで模型用の直流モータの回転速度をこれで制御したい…と考えるかもしれない。
しかし、直流モータは、ブラシとコイル(電磁石)を組み合わせたものだが、モーターが回転しだす瞬間でみれば、コイルは単なる導線である。このため、小さい電流でゆっくりモータを回転させようとすると、たとえ小さい電圧でも導線(抵抗はほぼ0[Ω])には大量の電流が流れ、モータをスイッチングする回路は焼き切れるかもしれない。
PWM変調
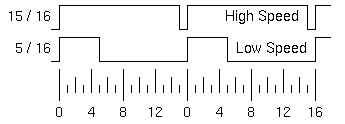
こういう場合には、PWM変調(Pulse Width Modulation) を行う。
このような波形であれば、低速度でも電流が流れる時間が短く、大量の電流消費は避けられ、モーターをまわす力も安定する。
A/D変換回路
D/A変換とは逆に、アナログ量をデジタル値に変換するには、どのようにするか?
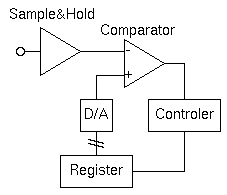
このような場合には、A/D変換回路を用いる。一般的な回路では、以下のような逐次比較型A/D変換を用いる。
この回路では、変換開始と共に入力値をサンプル保持回路でアナログ量を保存する。
その後、Registerの中のデジタル値を、D/A 変換回路でアナログ量に変換した結果を、比較器(Comparator)でどちらが大きいか判断し、その結果に応じて2分探索法とかハイアンドローの方式のように、比較を繰り返しながらデジタル値を入力値に近づけていく。
ハイアンドロー(数あてゲーム)
数あてゲームで、デタラメな0〜127までの整数を決めて、ヒントを元にその数字を当てる。回答者は、数字を伝えると、決めた数よりHighかLowのヒントをもらえる。
最も速い回答方法は…例えば決めた数が55だとすると
・初期状態 ??????? 0..127 ・64 - Low 0?????? 0..63 ・32 - High 01????? 32..63 ・48 - High 011???? 48..63 ・56 - Low 0110??? 48..55 ・52 - High 01101?? 52..55 ・54 - High 011011? 54..55 ・55 - Bingo 0110111 55確定どんな値でも、7回(27=127)までで当てることができる。
量子化と量子化誤差
アナログデータ(連続量)をデジタルデータなどの離散的な値で近似的に表すことを、量子化という。
量子化誤差とは、信号をアナログからデジタルに変換する際に生じる誤差のことをいう。
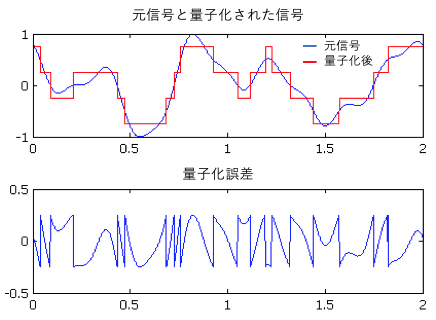
アナログ信号からデジタル信号への変換を行う際、誤差は避けられない。アナログ信号は連続的で無限の正確さを伴うが、デジタル信号の正確さは量子化の解像度やアナログ-デジタル変換回路のビット数に依存する。
偶然誤差
アナログ信号がA/D変換回路に入るまでに、アナログ部品の電気的変動(ノイズ)が原因で値が変動することもある。ノイズが時間的に不規則に発生し、値が増えてしまったり減ってしまったり偶然に発生するものは偶然誤差という。偶然誤差を加えると相殺されてほぼ0になるのであれば、統計的な手法で誤差の影響を減らすことができる。
数値と誤差
コンピュータで計算すると、計算結果はすべて正しいと勘違いをしている人も多い。ここで、改めて誤差について考える。
特に、A/D変換したような値であれば、値自体に誤差が含まれている。
こういった誤差が含まれる数字を扱う場合注意が必要である。例えば、12.3 と 12.300 では意味が異なる。測定値であやふやな桁を丸めたのであれば、前者は 12.25〜12.3499 の間の値であり有効数字3桁である。後者は、12.2995〜12.300499 の間の値であり、有効数字5桁である。このため、誤差が含まれる数字の加算・減算・乗算・除算では注意が必要である。
加減乗除算の場合
加減算であれば小数点の位置を揃え、誤差が含まれる桁は有効桁に含めてはいけない。

上記の計算では、0.4567の0.0567の部分は意味がないデータとなる。(情報落ち)
乗除算であれば、有効桁の少ない値と有効桁の多い値の計算では、有効桁の少ない方の誤差が計算結果に出てくるため、通常は、有効桁5桁と2桁の計算であれば、乗除算結果は少ない2桁で書くべきである。

桁落ち
有効桁が大きい結果でも、減算が含まれる場合は注意が必要である。
例えば、以下のような計算では、有効桁7桁どうしでも、計算結果の有効桁は3桁となる。

このような現象は、桁落ちと呼ばれる。
なぜデジタル信号を使うのか
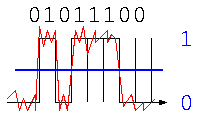
コンピュータが信号処理でなぜ使われるのか?例えば、下の信号のように、電圧の低い/高いで0/1を表現したとする。
このデータ”01011100″を通信相手に送る場合、通信の途中でノイズ(図中の赤)のような信号が加わった場合、アナログ信号では、どれがノイズなのか判別することはできない。しかしデジタル信号であれば、真ん中青線より上/下か?で判別すれば、ノイズの影響は無視して、元どおりの”01011100″を取り出せる。この0か1かを判別するための区切り(図中青線)は、しきい値と呼ばれる。
また、”01011100″のデータを送る通信の途中で、しきい値を越えるようなノイズが混ざって、受信したとする。この場合、単純に受け取るだけであれば、”01010100″で間違った値を受け取っても判別できない。しかし、データを送る際にパリティビット(偶数パリティであれば全データの1の数が偶数になるように)1ビットのデータを加える。このデータを受け取った際に、ノイズで1ビット反転した場合、1の数が奇数(3個)なので、ノイズでビット反転が発生したことがわかる。これをパリティチェックと言う。
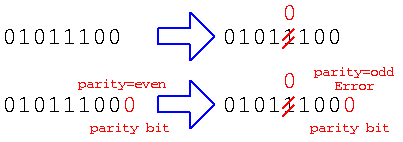
このように、デジタル信号を使えば、しきい値を越えない程度のノイズならノイズを無視できるし、たとえ大きなノイズでデータに間違いがあっても、パリティチェックのような方法を使えば間違って伝わったことを判別できる。
純粋仮想基底クラス
前回説明した仮想関数では、基底クラスから派生させたクラスを作り、そのデータが混在してもクラスに応じた関数(仮想関数)を呼び出すことができる。
この仮想関数の機能を逆手にとったプログラムの記述方法として、純粋仮想基底クラスがある。その使い方を説明する。
純粋仮想基底クラス
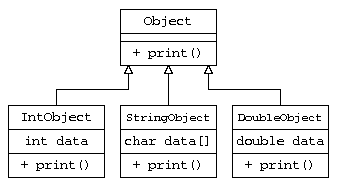
純粋仮想基底クラスとは、見かけ上はデータを何も持たないクラスであり、本来なら意味がないデータ構造となってしまう。しかし、派生クラスで仮想関数で機能を与えることで、基底クラスという共通部分から便利な活用ができる。(実際には、型を区別するための情報を持っている)
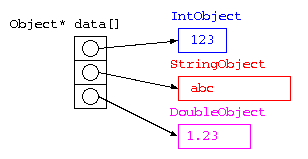
例えば、一つの配列に、整数、文字列、実数といった異なる型のデータを記憶させることは本来ならできない。しかし、以下のような処理を記載すれば、可能となる。
// 純粋仮想基底クラス
class Object {
public:
virtual void print() = 0 ;
// 中身の無い純粋基底クラスで、
// 仮想関数を記述しない時の書き方。
} ;
// 整数データの派生クラス
class IntObject : public Object {
private:
int data ;
public:
IntObject( int x ) {
data = x ;
}
virtual void print() {
printf( "%d\n" , data ) ;
}
} ;
// 文字列の派生クラス
class StringObject : public Object {
private:
char data[ 100 ] ;
public:
StringObject( const char* s ) {
strcpy( data , s ) ;
}
virtual void print() {
printf( "%s\n" , data ) ;
}
} ;
// 実数の派生クラス
class DoubleObject : public Object {
private:
double data ;
public:
DoubleObject( double x ) {
data = x ;
}
virtual void print() {
printf( "%lf\n" , data ) ;
}
} ;
// 動作確認
int main() {
Object* data[3] = {
new IntObject( 123 ) ,
new StringObject( "abc" ) ,
new DoubleObject( 1.23 ) ,
} ;
for( int i = 0 ; i < 3 ; i++ ) { // 123
data[i]->print() ; // abc
} // 1.23 と表示
return 0 ;
} ;
このプログラムでは、純粋仮想基底クラスObjectから、整数IntObject, 文字列StringObject, 実数DoubleObject を派生させ、そのデータを new により生成し、Objectの配列に保存している。
様々な型に適用できるプログラム
次に、純粋仮想基底クラスの特徴を応用したプログラムの作り方を説明する。
例えば、以下のような最大選択法で配列を並び替えるプログラムがあったとする。
int a[5] = { 11, 55, 22, 44, 33 } ;
void my_sort( int array[] , int size ) {
for( int i = 0 ; i < size - 1 ; i++ ) {
int max = i ;
for( int j = i + 1 ; j < size ; j++ ) {
if ( array[j] > array[max] )
max = j ;
}
int tmp = array[i] ;
array[i] = array[max] ;
array[max] = tmp ;
}
}
int main() {
my_sort( a , 5 ) ;
}
しかし、この整数を並び替えるプログラムがあっても、文字列の並び替えや、実数の並び替えがしたい場合には、改めて文字列用並び替えの関数を作らなければいけない。しかも、ほとんどが同じような処理で、改めて指定された型のためのプログラムを作るのは面倒である。
C言語のデータの並び替えを行う、qsort() では、関数ポインタを用いることで、様々なデータの並び替えができる。
#include <stdio.h> #include <stdlib.h> int a[ 4 ] = { 11, 33, 22, 44 } ; double b[ 3 ] = { 1.23 , 5.55 , 0.11 } ; // 並び替えを行いたいデータ専用の比較関数を作る // a>bなら+1, a=bなら0, a<bなら-1を返す関数 int cmp_int( int* pa , int* pb ) { return *pa - *pb ; } int cmp_double( double* pa , double* pb ) { if ( *pa == *pb ) return 0 ; else if ( *pa > *pb ) return 1 ; else return -1 ; } int main() { qsort( a , 4 , sizeof( int ) , (int(*)(void*,void*)) cmp_int ) ; qsort( b , 3 , sizeof( double ) , (int(*)(void*,void*)) cmp_double ) ; }
任意のデータを並び替え
class Object {
public:
virtual void print() = 0 ;
virtual int cmp( Object* ) = 0 ;
} ;
// 整数データの派生クラス
class IntObject : public Object {
private:
int data ;
public:
IntObject( int x ) {
data = x ;
}
virtual void print() {
printf( "%d\n" , data ) ;
}
virtual int cmp( Object* p ) {
int pdata = ((IntObject*)p)->data ;
return data - pdata ;
}
} ;
// 文字列の派生クラス
class StringObject : public Object {
private:
char data[ 100 ] ;
public:
StringObject( const char* s ) {
strcpy( data , s ) ;
}
virtual void print() {
printf( "%s\n" , data ) ;
}
virtual int cmp( Object* p ) {
char* pdata = ((StringObject*)p)->data ;
return strcmp( data , pdata ) ; // 文字列比較関数
}
} ;
// 実数の派生クラス
class DoubleObject : public Object {
private:
double data ;
public:
DoubleObject( double x ) {
data = x ;
}
virtual void print() {
printf( "%lf\n" , data ) ;
}
virtual int cmp( Object* p ) {
double pdata = ((DoubleObject*)p)->data ;
if ( data == pdata )
return 0 ;
else if ( data > pdata )
return 1 ;
else
return -1 ;
}
} ;
// Objectからの派生クラスでcmp()メソッドを
// 持ってさえいれば、どんな型でもソートができる。
void my_sort( Object* array[] , int size ) {
for( int i = 0 ; i < size - 1 ; i++ ) {
int max = i ;
for( int j = i + 1 ; j < size ; j++ ) {
if ( array[j]->cmp( array[max] ) > 0 )
max = j ;
}
Object* tmp = array[i] ;
array[i] = array[max] ;
array[max] = tmp ;
}
}
// 動作確認
int main() {
Object* idata[3] = {
new IntObject( 11 ) ,
new IntObject( 33 ) ,
new IntObject( 22 ) ,
} ;
Object* sdata[3] = {
new StringObject( "abc" ) ,
new StringObject( "defghi" ) ,
new StringObject( "c" ) ,
} ;
my_sort( idata , 3 ) ; // 整数のソート
for( int i = 0 ; i < 3 ; i++ )
idata[i]->print() ;
my_sort( sdata , 3 ) ; // 文字列のソート
for( int i = 0 ; i < 3 ; i++ )
sdata[i]->print() ;
return 0 ;
} ;
このような方式でプログラムを作っておけば、新しいデータ構造がでてきてもソートのプログラムを作らなくても、比較専用の関数 cmp() を書くだけで良い。
ただし、この並び替えの例では、Object* を IntObject* に強制的に型変換している。
また、このプログラムでは、データを保管するために new でポインタを保管し、データの比較をするために仮想関数の呼び出しを行うことから、メモリの使用効率も処理効率でもあまりよくない。こういう場合、最近の C++ ではテンプレート機能が使われる。
template <typename T> void my_sort( T a[] , int size ) { for( int i = 0 ; i < size - 1 ; i++ ) { int max = i ; for( int j = i + 1 ; j < size ; j++ ) { if ( a[j] > a[max] ) max = j ; } T tmp = a[i] ; a[i] = a[max] ; a[max] = tmp ; } } int main() { int idata[ 5 ] = { 3, 4, 5 , 1 , 2 } ; double fdata[ 4 ] = { 1.23 , 0.1 , 3.4 , 5.6 } ; my_sort( idata , 5 ) ; for( int i = 0 ; i < 5 ; i++ ) printf( "%d " , idata[i] ) ; printf( "\n" ) ; my_sort( fdata , 4 ) ; for( int i = 0 ; i < 4 ; i++ ) printf( "%lf " , fdata[i] ) ; printf( "\n" ) ; return 0 ; }C++のテンプレート機能は、my_sort( int[] , int ) で呼び出されると、typename T = int で、整数型用の my_sort() の処理が自動的に作られる。同じく、my_sort( double[] , int ) で呼び出されると、typename = double で 実数型用の my_sort() が作られる。