JavaScriptの再帰の例題
再帰呼び出しで分割統治法の考え方のプログラムをJavaScriptで書いたサンプル
単純に、配列の指定範囲の合計を求める関数を、再帰を用いて記述する。
<html>
<head>
</head>
<body>
<p>
このプログラムは、実行結果を console.log() で出力するので、
Ctrl+Shift+I で、JavaScript の console を表示させてね。
</p>
<script type="text/javascript">
// a : 配列
// start : 合計を計算する範囲の戦闘
// end : 合計を計算する範囲の最後+1
// 配列の合計は、配列の先頭 + 残りの合計
function array_sum( a , start , end ) {
console.log( "array_sum:" + start + "," + end ) ;
if ( start == end ) {
console.log( "array_sum(" + start + "," + end + ")=0" ) ;
return 0 ;
} else {
var ans = a[ start ] + array_sum( a , start + 1 , end ) ;
console.log( "array_sum("+start+","+end+")="+ans ) ;
return ans ;
}
}
var array = new Array( 11 , 22 , 33 , 44 , 55 , 66 , 77 , 88 ) ;
console.log( array_sum( array , 0 , array.length ) ) ;
// 配列の合計は、データが1個ならその値。
// そうでなければ、配列の前半の合計 + 配列の後半の合計
function array_sum2( a , start , end ) {
console.log( "array_sum2:" + start + "," + end ) ;
if ( start + 1 == end ) {
var ans = a[ start ] ;
console.log( "array_sum2("+start+","+end+")="+ans ) ;
return ans ;
} else {
var mid = Math.floor( ( start + end ) / 2 ) ;
var ans = array_sum2( a , start , mid ) // 配列前半の合計を求める
+ array_sum2( a , mid , end ) ; // 配列後半の合計を求める
console.log( "array_sum2("+start+","+end+")="+ans ) ;
return ans ;
}
}
console.log( array_sum2( array , 0 , array.length ) ) ;
</script>
</body>
</html>
データベースの設計と正規形
適切でないデータベースを例にしながら、更新不整合が発生することを説明する。 (不整合には、修正不整合・挿入不整合・削除不整合がある。) この不整合が発生しないデータベース(表)を作るためには、どうすべきかを解説。
ERモデル
不整合が起こらないようなデータベースとするには、実体と関連にモデル化を行う。 実体・関連には、属性(attribute)が付随し、実体を長方形、関連をひし形、属性を楕円で表現する ER図を描く。

学生や教員といった実体は、人という汎化した視点であれば、識別番号と名前の属性で 表現できると意味で、共通である。人を学生という視点で特化した先に、学科名や学年といった 属性を持つと考えられる。こういった汎化階層は、オブジェクト指向と同じ。
実体の中には、他の実体と関連を持って初めて意味を持つ実体もある。 関連先の実体が消えれば、存在自体が無意味になってしまう実体は、弱実体と呼ぶ。
正規形
データベースにおいて、様々な不整合を防ぐために正しい設計が必要であることを 改めて説明し、それには正規形としての条件を満たしている必要があることを説明する。
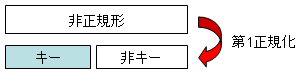
第一正規形は、すべての要素が原子値である条件を満たせばいい。 要素の中が複数の項目であったり表形式のデータがあると、 表構造のリレーショナルデータベースにはできない。
キーの説明:超キー(スーパーキー)とは、データベースで1つのデータを 選び出すために必要なデータ項目であり、複数の項目で1データを指定 できる場合もある。
候補キーとは、必要最小限の項目となっているものを指す。 1項目が抜けても選別できなくなるようであれば、候補キーとは言わない。 主キーとは、候補キーのなかで管理の都合上便利なもの。
データ項目の値が決まると、他のデータ項目が自動的に決まるものは、 従属関係があるという。
 |
 |
| 第1正規化 | 第2正規化 |
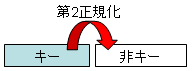
第二正規形は、部分従属がなく、すべての非キーデータ項目が、候補キーに 完全従属する場合をいう。
完全従属とは、候補キーを構成する全てのデータ項目に、非キーデータ項目が従属していること。 部分従属とは、候補キーを構成するデータ項目の一部のデータ項目に、非キー項目が従属していること。
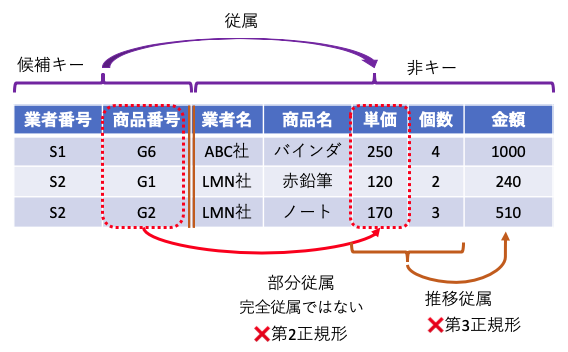
この例において、単価は商品が決まれば自動的に求まる情報。 (単価が日々変化することはないという条件で…) これは、部分従属となる。
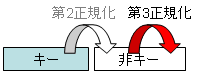
推移従属性とは、データ項目でA→B→Cと、次々と値が求められる関係を指す。 このなかで、第三正規形とは、 候補キー以外の非キーデータ項目は、候補キーに完全従属し、 かつどの候補キーにも推移従属しない関係をいう。
 |
| 第3正規化 |
上記の例では、単価と個数が決まれば、金額が求まる推移従属の関係が含まれている。
おまけ:BC正規形,第4,5正規形
この他にも、 さらに非キーからキーに関数従属性がある場合にそれを取り除く、 ボイスコッド正規形(BC正規化)。 「対称性のある多値従属性(キーを決めると複数データが該当)」を分解して得られる第4正規形や、 「元になるテーブルの結合従属性を維持して分解することにより得られる第5正規形などがある。

トランスポート層・TCPとUDP
サブネット同士をつなぐプロトコルとして、IPプロトコルを紹介したが、データ通信ではノイズなどの影響で通信に失敗することがある。これらを補うためのTCPがある。
TCP
TCP(Transmission Control Protocol/トランスミッションコントロールプロトコル)では、分割されたパケットを元の順序に組み上げたり、パケットが途中で消えた場合の再送などの処理を行う。この機能により確実に相手に送る機能が実現されている。
3way ハンドシェーク
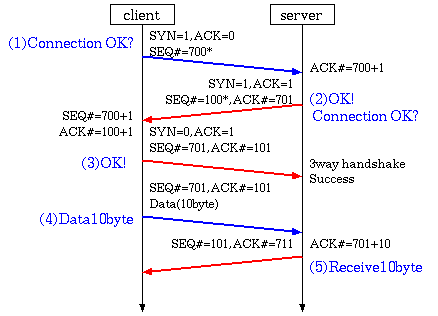
TCPの通信では、最初に相互に通信が可能かを確認するハンドシェークが行われる。パケットには、SYN,ACK,FINといった種別を表すフラグがついており、SYNは接続確立の要求を表す。ACKは了解を表す。FINは切断要求を表す。通信開始の時には、(1)通信OK?、(2)OKだよ,そっちもOK?、(3)OKだよ! といった3つの通信パケットで確認してから通信を行う。この最初のやり取りを3way ハンドシェークという。
- SYN flood攻撃 – 3wayハンドシェークは、今後のパケット並び替えの準備も含めるとコストが高い。通信ルールを無視して相手にSYNパケットだけを大量に送ると相手は他の通信が困難になる場合がある。
SEQ番号,ACK番号
また、通信パケットには、SEQ番号とACK番号という情報がついており、3wayハンドシェーク時には、相手のSEQ番号に1を加えたACK番号をつけてパケットを返送する。これにより、どの通信に対する返事か判るようにしている。さらに、実際のデータを送信する際には、受け取ったデータ長をSEQ番号に加えた値を、ACK番号にして受信に成功したことを相手に伝える。これにより、小分けにされたパケットで次に何を送れば良いのか判別できる。
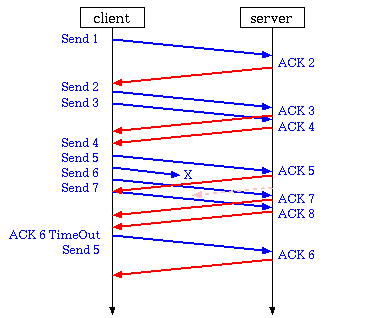
通信で、パケット分割して送って、その一つ毎の返答を待つと、通信の待ち時間が増えてしまう。このため、相手が受け取り可能であれば、一度に前回の2倍のパケットを返信を待たずに送る。(ウィンドウサイズの拡大)
チェックサムとタイムアウト
通信では、送る途中でデータにノイズが混入したり、パケットが消失することがある。このため、パケットにはパケットのチェックサム(バイトデータを加算した値)を付けて送り、受信時に比較してノイズ混入を確認する。こういった際には、パケットが正しく届かない。パケットが消失したりして、通信相手からの返送が届かないで一定の待ち時間が経過することをタイムアウトと呼ぶ。この時、返信パケットにはデータのSEQ番号とACK番号の情報があるため、受け取りに失敗したパケットが判別できるので、送り側は失敗したパケットを再送する。
受け取り側は、同じくSEQ番号やACK番号を元にパケットの順番を正しく並べ戻すことができる。
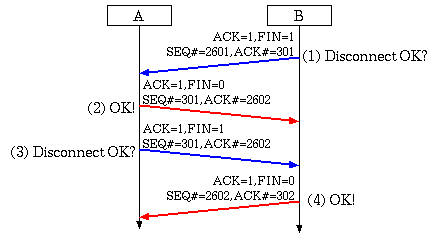
TCP FINパケット
通信を切断する場合には、相互に切断して良いか確認する4回の通信で終了する。
UDP
TCPによる通信は、相手側からの受け取った返事を待ちながら通信を行う。このため、通信にかかる時間を要する。また、複数の利用者に一斉にデータをばらまくブロードキャスト通信では、個別のパケット欠落を修復しようとすると、処理が複雑になる。
これらの対応策として、UDP(User Datagram Protocol)がある。これは、TCP通信でのパケット分割や再送処理を行わない極めて単純な送信方法である。このため、相手側に正しくデータが送られる保証はない。確実に相手に送る必要があれば、確認や再送は上位プロトコルの責任となる。
UDP通信は、動画・音声配信などのリアルタイム性のある通信で、正しく通信ができず一時的に動画が止まるなり音声が止まっても、問題が少ないような場合に有効となる。
トランスポート層
OSI参照モデルでは、TCPプロトコルとUDPプロトコルをあわせてトランスポート層と呼び、TCP+UDPとIPプロトコルでの通信が、今日のインターネット通信の基本プロトコルとなっており、総称して TCP/IPとかインターネット・プロトコル・スイート と呼ぶ。
データベースの設計とER図
データベースの設計
リレーショナル・データベースでは、データは表形式であればなんでも良い訳ではない。
例えば、学生の成績データが以下のような構造であった場合、
ID | name | grade | subject | teacher ------+--------+-------+----------+--------- 20101 | aoyama | 1 | database | saitoh 20101 | aoyama | 1 | software | murata 20002 | suzuki | 2 | database | saitoh 20002 | suzuki | 2 | compiler | nomura 30203 | yamada | 3 | media | ogoshi
- 修正不整合: 授業担当が saitoh → sasaki のように変更になったら、複数のテーブルを修正しなければならない。
- 挿入不整合: 新しい科目 internet を追加したいけど、受講学生が決まらないとデータを挿入できない。
- 削除不整合: yamada が受講を取りやめたら、科目 media も消えてしまう。
これらを考慮すると、以下のような3つの表で設計するべきである。
学生 受講 科目
ID | name | grade ID | SubID SubID | subject | teacher
------+--------+------- ------+------- ------+----------+--------
20101 | aoyama | 1 20101 | 1001 1001 | database | saitoh → sasaki
20002 | suzuki | 2 20101 | 1002 1002 | software | murata
30203 | yamada | 3 20002 | 1001 1003 | compiler | nomura
20002 | 1003 1004 | media | ogoshi
消す→ 30203 | 1004 1005 | internet | foobar → 追加
データベースの設計では、(1)概念設計、(2)論理設計、(3)物理設計が行われる。
- 概念設計:概念スキーマの決定(実体・関係モデルを使う)。上記の受講データベースの設計例
- 論理設計:論理スキーマの決定。関係データベースで実装?ほかのデータベース?
- 物理設計:物理スキーマの決定。データの格納方法や管理方法を決める。
実体関連モデル(ERモデル)
データベース設計では、実体関連モデル(ERモデル:Entity-Relation model)が使われる。 実体とは、モデル化しようとする対象で独立した存在となれるもの。 実体が持つ色々な特性は属性と呼ばれる。 属性の取りうる値の集合を定義域、同一種類の実体の集まりを実体集合と呼ぶ。 関連とは、実体同士の相互関係をモデル化したもの。
実体関連図(ER図)では、実体を長方形、関連をひし形、属性を楕円で表現する。 属性で、キーとなるものには下線をつけて表す。

ER図で調べると、実際にはもっと細かい規定で表現が行われている。 参考:IDEF1X表記とIE表記
演算子と2分木による式の表現
2分木の応用として、式の表現を行うけどその前に…
逆ポーランド記法
一般的に 1*2 + 3*4 と記載すると、数学的には演算子の優先順位を考慮して、(1*2)+(3*4) のように乗算を先に行う。このような優先順位を表現する時に、()を使わない方法として、逆ポーランド記法がある。
演算子の書き方には、前置記法、中置記法、後置記法があり、後置記法は、「2と3を掛ける、それに1を加える」と捉えると、日本語の処理と似ている。
中置記法 1+2*3 前置記法 +,1,*,2,3 後置記法 1,2,3,*,+
後置記法は、一般的に逆ポーランド記法(Reverse Polish Notation)とも呼ばれ、式を機械語の命令に置き換える際に役立つ。
理解度確認
以下の式を指定された書き方で表現せよ。
逆ポーランド記法 1,2,*,3,4,*,+ を中置記法で表現せよ。 中置記法 (1+2)*3-4*5 を逆ポーランド記法で表現せよ。
以前の情報処理技術者試験では、スタックの概念の理解の例題として、逆ポーランド記法への変換アルゴリズムのプログラム作成が出題されることが多かったが、最近は出題されることはなくなってきた。
逆ポーランド式の実行
この逆ポーランド記法で書かれた式から結果を求めるプログラムは以下のように記述できる。このプログラムでは式を簡単にするため、数値は1桁の数字のみとする。
// 単純な配列を用いたスタック
int stack[ 10 ] ;
int sp = 0 ;
void push( int x ) {
stack[ sp++ ] = x ;
}
int pop() {
return stack[ --sp ] ;
}
// 逆ポーランド記法の計算
int rpn( char* p ) {
for( ; *p != '\0' ; p++ ) {
if ( isdigit( *p ) ) {
// ~~(A)
push( *p - '0' ) ;
} else if ( *p == '+' ) {
int r = pop() ;
int l = pop() ;
push( l + r ) ;
} else if ( *p == '*' ) {
int r = pop() ;
int l = pop() ;
push( l * r ) ;
}//~~~~~~~~~~~~~(B)
}
return pop() ;
}
void main() {
printf( "%d\n" , rpn( "123*+" ) ) ;
}
逆ポーランド記法の式の実行は、上記のようにスタックを用いると簡単にできる。このようなスタックと簡単な命令で複雑な処理を行う方法はスタックマシンと呼ばれる。Java のバイトコードインタプリタもこのようなスタックマシンである。
Cプログラママニア向けの考察
上記のプログラムでは、int r=pop();…push(l+r); で記載しているが、
push( pop() + pop() ) ;とは移植性を考慮して書かなかった。理由を述べよ。
最初の関数電卓
初期の関数電卓では複雑な数式を計算する際に、演算子の優先順位を扱うのが困難であった。このため、HP社の関数電卓では、式の入力が RPN を用いていた。(HP-10Cシリーズ)
2項演算と構文木
演算子を含む式が与えられたとして、それを保存する場合、演算式の2分木で扱うと都合が良い。
+ / \ 1 * / \ 2 3
演算子の木のノードで、末端は数値であることに注目し、右枝・左枝がNULLなら数値(data部にはその数値)、それ以外は演算子(data部には演算子の文字コード)として扱うとして…
struct Tree {
int data ;
struct Tree* left ;
struct Tree* right ;
} ;
struct Tree* tree_int( int x ) // 数値のノード
{
struct Tree* n ;
n = (struct Tree*)malloc( sizeof( struct Tree ) ) ;
if ( n != NULL ) {
n->data = x ;
n->left = n->right = NULL ;
}
return n ;
}
struct Tree* tree_op( int op , // 演算子のノード
struct Tree* l , struct Tree* r ) {
struct Tree* n ;
n = (struct Tree*)malloc( sizeof( struct Tree ) ) ;
if ( n != NULL ) { // ~~~~~~~~~~~~~~~~~~~~~(C)
n->data = op ;
n->left = l ;
n->right = r ;
}
return n ;
}
// 与えられた演算子の木を
int eval( struct Tree* p ) {
if ( p->left == NULL && p->right == NULL )
return p->data ;
else
switch( p->data ) {
case '+' : return eval( p->left ) + eval( p->right ) ;
case '*' : return eval( p->left ) * eval( p->right ) ;
} // ~~~~~~~~~~~~~~~(D) ~~~~~~~~(E)
}
void main() {
struct Tree* exp =
tree_op( '+' ,
tree_int( 1 ) ,
tree_op( '*' ,
tree_int( 2 ) , tree_int( 3 ) ) ) ;
printf( "%d¥n" , eval( exp ) ) ;
}
理解度確認
- 上記プログラム中の(A),(B),(C),(D)の型を答えよ。
ネットワーク層とIPアドレス
前回説明したMACアドレスによるデータリンク層では、1つのサブネットの中で指定した相手にデータを送ることはできる。しかし、データリンク層だけでは、他のサブネットにいる相手にデータを送ることができない。(相手の名前を知っていても、住所を知らなければ郵便は送れない。)
ネットワーク層とIPアドレス(IPv4)
サブネットに分割し、隣接するサブネット、さらには上流のインターネットと通信をするためには、IPアドレスを用いた通信が行われる。
ネットワークに接続する機器には、それぞれユニークな32bitの番号(IPv4アドレス)を割り振る。
コンピュータへのIPアドレスの設定には、(a)IPアドレス,(b)サブネットマスク,(c)ゲートウェイの情報が必要となる。
- IPアドレス: 192.156.145.100 といった、0~255の8bitの値をピリオド区切りで4つ並べて表記するのが一般的。
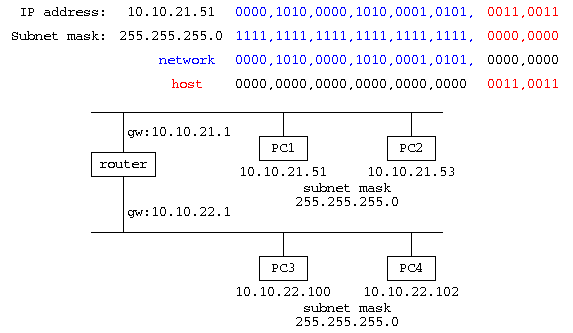
- サブネットマスク: 255.255.255.0 といった値で、IPアドレスを2進数で書き並べた32bitと、サブネットマスクの32bitで、2進数の論理積をとった値は、ネットワーク番号と呼ばれ、機器が存在する場所を表す。
また、IPアドレスとサブネットマスクの否定と論理積をとった値は、ホスト番号と呼ばれる。 - ゲートウェイ: 自分自身のネットワーク番号と通信相手のネットワーク番号が異なる場合は、異なるサブネットにいるので、パケットを中継してもらう機器(ルータ,ゲートウェイ)にパケットを送る。

ARP(IPアドレスとMACアドレスの橋渡し)
同じサブネットの中では、データリンク層でMACアドレスを用いて通信相手を指定するが、ネットワーク層ではIPアドレスを用いて通信相手を指定する。この違いを埋めるためのプロトコルがARPである。
サブネット内に相手先IPアドレスの指定されたパケット(10.10.22.102)が届くと、通信機器はサブネット内の全ての機器相手に ARPリクエストを送信する。(10.10.22.102はいますか?)
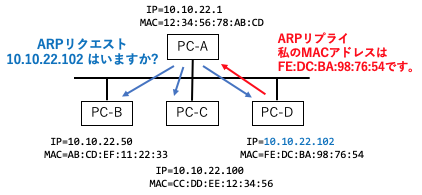
この時、10.10.22.102 のコンピュータは、自分宛てのパケットがあることを知るので、送信元のコンピュータに、自分のMACアドレスを付けたARPリプライを送り返す。(10.10.22.102は、私 “FE:DC:BA:98:76:54” です!)。送信元は、ARP通信をへらすために、その情報を記憶して、2度目以降は覚えたMACアドレスですぐに通信を始める。
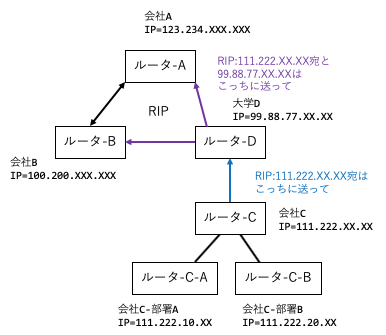
ルータとRIP
ルータは、隣接するサブネットの間に入る機器で、各サブネットにゲートウェイとなるインタフェースを持つ。ルータには、RIPというプロトコルにより、各サブネットのつながっている経路情報が送られてくる。この経路情報を見て、パケットのIPアドレスを見て、パケットの送り先を判断する。
((Windows の場合))
C:> ipconfig /all
インタフェース名:
IPv4アドレス............192.168.xx.xx
サブネットマスク.........255.255.255.0
デフォルトゲートウェイ....192.168.xx.1
C:> arp -a
インタフェース:
192.168.xx.xx 74-03-xx-xx-xx-xx 動的
192.168.xx.yy B0-05-xx-xx-xx-xx 動的
C:> netstat -r
ネットワーク宛先 ネットマスク ゲートウェイ インタフェース メトリック
0.0.0.0 0.0.0.0 192.168.xx.1 192.168.xx.xx 45
192.168.xx.0 255.255.255.0 ....
((Unix の場合))
$ ifconfig -a
en1: ....
inet 192.168.xx.xx netmask 0xffffff00 ...
$ arp -an
.... (192.168.xx.xx) at 74:03:xx:xx:xx:xx ...
.... (192.168.xx.yy) at b0:05:xx:xx:xx:xx ...
$ netstat -rn
Destination Gateway ...
default 192.168.xx.1 ...
192.168.xx ...
プライベートアドレス
IPv4 では、32bit でコンピュータを識別することから、最大でも 232台≒40億台しか識別できない。実際、IPアドレスの管理団体では、2017年度には IPv4 アドレスは使い切った状態となっている。この対応として、その組織やその家庭内だけで使われる IPアドレス である、プライベートアドレスが用いられる。
- 10.0.0.0~10.255.255.255 / 8 – 大きな機関向け
- 172.16.0.0~172.31.255.255 / 12
- 192.168.0.0~192.168.255.255 /16 – 個人向け
プライベートアドレスを利用する組織では、インターネットに接続するルータでは NAT(もしくはNAPT) という機能を内蔵し、プライベートアドレスとグローバルアドレスの変換を行う。
理解確認
- Cクラスのサブネットに設置できるコンピュータの台数は何台?
- “172.”で始まるプライベートアドレスでは最大何台?
- 192.168.11.2/24 のコンピュータから、192.168.1.50にデータを送る場合、どのような処理が行われるか、IPアドレス、サブネットマスク、ゲートウェイ、ネットワーク番号を使って説明せよ。
- 同じサブネット内で相手のIPアドレスが与えられた時、どのようにパケットが送られるか、MACアドレスとARPを交えて説明せよ。
コンパイラと関数電卓プログラム(専攻科実験2018)
専攻科1年・生産システム実験1(後期)の「コンパイラと関数電卓プログラム」の説明は、昨年度資料と共通なのでリンクを記載しておく。
意思決定木と構文解析
意思決定木
意思決定木の説明ということで、yes/noクイズの例を示しながら、2分木になっていることを 説明しプログラムを紹介。
((意思決定木の例:うちの子供が発熱した時)) 38.5℃以上の発熱がある? no/ \yes 元気がある? むねがひいひい? yes/ \no no/ \yes 様子をみる 氷枕で病院 解熱剤で病院 速攻で病院
このような判断を行うための情報は、yesの木 と noの木の2つの枝を持つデータである。これは2分木と同じであり、このような処理は以下のように記述ができる。
struct Tree {
char *qa ;
struct Tree* yes ;
struct Tree* no ;
} ;
struct Tree* dtree( char *s ,
struct Tree* l , struct Tree* r )
{ struct Tree* n ;
n = (struct Tree*)malloc( sizeof( struct Tree ) ) ;
if ( n != NULL ) {
n->qa = s ;
n->yes = l ;
n->no = r ;
}
return n ;
}
void main() {
struct Tree* p =
dtree( "38.5℃以上の発熱がある?" ,
dtree( "胸がひぃひぃ" ,
dtree( "速攻で病院",NULL,NULL ) ,
dtree( "解熱剤で病院",NULL,NULL ) ) ,
dtree( "元気がある?" ,
dtree( "様子をみる",NULL,NULL ) ,
dtree( "氷枕で病院",NULL,NULL ) ) ) ;
struct Tree* d = p ;
while( d->yes != NULL || d->no != NULL ) {
printf( "%s¥n" , d->qa ) ;
scant( "%d" , &ans ) ;
if ( ans == 1 )
d = d->yes ;
else if ( ans == 0 )
d = d->no ;
}
printf( "%s¥n" , d->qa ) ;
}
コンパイラと言語処理系
高級言語で書かれたプログラムを計算機で実行するソフトウェアは、言語処理系と呼ばれる。その実行形式により
- インタプリタ(interpreter:翻訳)
- ソースプログラムの意味を解析しながら、その意味に沿った処理を行う
- コンパイラ(compiler:通訳)
- ソースプログラムから機械語を生成し、実行する際には機械語を実行
- トランスコンパイラ:ソースから他の言語のソースコードを生成し、それをさらにコンパイルし実行
- バイトコードインタプリタ:ソースからバイトコード(機械語に近いコードを生成)、実行時にはバイトコードの命令に沿った処理を行う
に分けられる。
コンパイラが命令を処理する際には、以下の処理が行われる。
- 字句解析(lexical analysys)
文字列を言語要素(token)に分解 - 構文解析(syntax analysys)
tokenの並び順に意味を反映した構造を生成 - 意味解析(semantics analysys)
命令に合わせた中間コードを生成 - 最適化(code optimization)
中間コードを変形して効率よいプログラムに変換 - コード生成(code generation)
実際の命令コードとして出力
バイトコードインタプリタとは
例年だと説明していなかったけど最近利用されるプログラム言語の特徴を説明。通常、コンパイラとかインタプリタの説明をすると、Java がコンパイラとか、JavaScript はインタプリタといった説明となる。しかし、最近のこういった言語がどのように処理されるのかは、特殊である。
(( Java の場合 )) foo.java (ソースコード) ↓ Java コンパイラ foo.class (中間コード) ↓ JRE(Java Runtime Engine)の上で 中間コードをインタプリタ方式で実行
あらかじめコンパイルされた中間コードを、JREの上で中間コードをインタプリタ的に実行するものは、バイトコードインタプリタ方式と呼ぶ。
ただし、JRE でのインタプリタ実行では遅いため、最近では JIT コンパイラにより、中間コードを機械語に変換してから実行する。
また、JavaScriptなどは(というか最近のインタプリタの殆どPython,PHP,Perl,…は)、一般的にはインタプリタに分類されるが、実行開始時に高級言語でかかれたコードから中間コードを生成し、そのバイトコードをインタプリタ的に動かしている。
しかし、インタプリタは、ソースコードがユーザの所に配布されて実行するので、プログラムの内容が見られてしまう。プログラムの考え方が盗まれてしまう。このため、変数名を短くしたり、空白を除去したり(…部分的に暗号化したり)といった難読化を行うのが一般的である。
トークンと正規表現(字句解析)
規定されたパターンの文字列を表現する方法として、正規表現(regular expression)が用いられる。
((正規表現の書き方)) 選言 「abd|acd」は、abd または acd にマッチする。 グループ化 「a(b|c)d」は、真ん中の c|b をグループ化 量化 パターンの後ろに、繰り返し何回を指定 ? 直前パターンが0個か1個 「colou?r」 * 直前パターンが0個以上繰り返す 「go*gle」は、ggle,gogle,google + 直前パターンが1個以上繰り返す 「go+gle」は、gogle,google,gooogle
正規表現は、sed,awk,Perl,PHPといった文字列処理の得意なプログラム言語でも利用できる。こういった言語では、以下のようなパターンを記述できる。
[文字1-文字2...] 文字コード1以上、文字コード2以下 「[0-9]+」012,31415,...数字の列 ^ 行頭にマッチ $ 行末にマッチ ((例)) [a-zA-Z_][a-zA-Z_0-9]* C言語の変数名にマッチする正規表現
構文とバッカス記法
言語の文法を表現する時、バッカス記法(BNF)が良く使われる。
((バッカス記法)) 表現 ::= 表現1... | 表現2... | 表現3... | ... ;
例えば、加減乗除記号と数字だけの式の場合、以下の様なBNFとなる。
((加減乗除式のバッカス記法))
加算式 ::= 乗算式 '+' 乗算式
| 乗算式 '-' 乗算式
| 乗算式
;
乗算式 ::= 数字 '*' 乗算式
| 数字 '/' 乗算式
| 数字
;
数字 ::= [0-9]+
;
上記のバッカス記法には、間違いがある。”1+2+3″を正しく認識できない。どこが間違っているだろうか?
このような構文が与えられた時、”1+23*456″と入力されたものを、“1,+,23,*,456”と区切る処理が、字句解析である。
また、バッカス記法での文法に合わせ、以下のような構文木を生成するのが構文解析である。
+ / \ 1 * / \ 23 456
理解度確認
- インタプリタ方式で、処理速度が遅い以外の欠点をあげよ。
- 情報処理技術者試験の正規表現,BNF記法問題にて理解度を確認せよ。
北陸イノベーショントライアルにてキャンパス部門優秀賞🎉

11月7日(火)に石川県立音楽堂で行われたHIT2018(第5回ビジネスモデル発見&発表会 北陸大会 および 起業家甲子園・起業家万博 北陸予選)に、福井高専の高専プロコンと専攻科学生による合同チームが参加し、キャンパス部門優秀賞と起業家甲子園挑戦権を獲得しました。

GROUP BY-HAVINGとCREATE VIEW
先週に引き続き、2つのSQLとそれと同じ処理のプログラム作成の課題に取り組む。
演習だけでは進度が少ないので、SQL で説明できなかった、GROUP BY-HAVING と CREATE VIEW の説明
GROUP BY HAVING
GROUP BY-HAVING では、指定されたカラムについて同じ値を持つレコードがグループ化される。SELECT 文に指定される集約関数は、グループごとに適用される。HAVING は、ある条件を満たす特定のグループを選択するための条件で、WHERE と違い、集約関数が使える。
SELECT SG.商品番号, SUM(SG.在庫量) FROM SG GROUP BY SG.商品番号 HAVING SUM(SG.在庫量) >= 500 ;
このSQLを実行すると、SG のテーブルから、商品番号が同じものだけをあつめてグループ化される。そのグループごとに在庫量のデータの合計SUMを集約し、500以上のデータが出力される。
CREATE VIEW
今までで述べてきたSQLでは、実際のテーブルを対象に、結合・選択・射影を行う命令であり、これは概念スキーマと呼ばれる、対象となるデータベース全体を理解したプログラマによって扱われる。
しかし、プログラムの分業化を行い、例えば結果の表示だけを行うプログラマにしてみれば、全てのデータベースの表を考えながらプログラムを作るのは面倒である。そこで、結合・選択・射影の演算の結果で、わかりやすい単純な表となったものであれば、初心者のデータベースプログラマでも簡単に結果を扱うことができる。このような外部スキーマを構成するための機能が、ビューテーブルである。
-- 優良業者テーブルを作る --
CREATE VIEW 優良業者 ( 業者番号 , 優良度 , 所在 )
AS SELECT S.業者番号, S.優良度, S.所在
FROM S
WHERE S.優良度 >= 15 ;
-- 優良業者テーブルから情報を探す --
SELECT *
FROM 優良業者
WHERE 優良業者.所在 = '福井' ;
ビューテーブルに対する SQL を実行すると、システムによっては予め実行しておいた CREATE VIEW の AS 以下の SQL の実行結果をキャッシュしておいて処理を行うかもしれない。システムによっては SQL の命令を 副クエリを組合せた SQL に変換し、処理を行うかもしれない。しかし、応用プログラマであれば、その SQL がどのように実行されるかは意識する必要はほとんど無いであろう。
ただし、ビューテーブルに対する 挿入・更新・削除といった演算を行うと、データによっては不整合が発生することもあるので注意が必要である。
