AVLと2分ヒープ
前回、2分探索木へのデータ追加の説明と、演習課題を行っていたが、演習時間としては短いので、今日も前半講義で残り時間は演習とする。
2分探索木へのデータ追加と不均一な木の成長
先週の講義で説明していた、entry() では、データを追加すべき末端を探し、追加する処理であった。
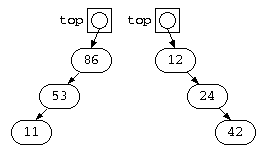
しかし、前回のプログラムで、以下のような順序でデータを与えたら、どのような木が出来上がるであろうか？
- 86, 53, 11 – 降順のデータ
- 12, 24, 42 – 昇順のデータ
この順序でデータが与えられると、以下のような木が出来上がってしまう。このような木では、データを探しても1回の比較でもデータ件数が1つ減るだけで、O(N)となってしまう。通常のデタラメな順序でデータが与えられれば、木はほぼ左右均等に成長するはずである。
AVL木
このような、不均一な木が出来上がっても、ポインタの繋ぎ変えで検索回数を改善できる。例えば、以下のような木では、赤の左側に偏っている。
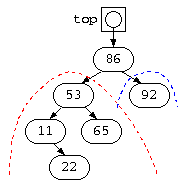
このような場合でも、最初、青の状態であっても、不均一な部分で赤のようなポインタの繋ぎ変えを行えば、木の段数を均一に近づけることができる。この例では、11,65,92の木が、右回転して 11 の木の位置が上がっている。(右回転)
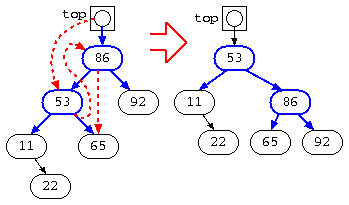
この様に、左右の枝の大きさが不均一な場所を見つけ、右回転や左回転を行う処理を繰り返すことで、段数が均一な2分探索木に修正ができる。この様な処理でバランスの良い木に修正された木は、AVL木と呼ばれる。
理解確認
- 木の根からの段数を求める関数 tree_depth() を作成せよ。
例えば、上のAVL木の説明の図であれば、4段なので4を返すこと。
// 木の段数を数える関数
_____ tree_depth( _______________ p ) {
if ( p == NULL ) {
return _____ ;
} else {
int d_L = ______________ ;
int d_R = ______________ ;
if ( d_L > d_R )
return _____ ;
else
return _____ :
}
}
// pをつなぎ替え上部を返り値で返す。
struct Tree*rot_right( struct Tree* p ) {
// p
// / \
// pl
// / \
// pr
struct Tree* pl = p->left ;
struct Tree* pr = pl->right ;
pl->right = p ;
p->left = pr ;
return pl ;
}
int main() {
printf( "%d¥n" , tree_depth( top ) ) ;
top = rot_right( top ) ;
return 0 ;
}
2分ヒープ(binary heap)
2分探索木では、１つのノードにつき2つのポインタを持ち、データ1件あたりのメモリの使用量が多い。通常の「配列の先頭から昇順にデータを並べる2分探索法」では、途中にデータを挿入する場合、データを後ろにずらす必要があるため、O(N)の処理時間を要する。
これらの問題の解決法の１つとして、2分ヒープがある。左右に均一に成長している2分探索木で、上から番号を以下の様に振ると、i番目のデータの左の枝は 2×i+1 番目、右の枝は 2×i+2 番目であることが判る。(自分の親のノードは、(i-1)/2 番目)
このような順序で配列にデータを保存する方法が2分ヒープである。この方式ならアルゴリズムの説明は省略するが、O(log(N))で挿入が可能となる。
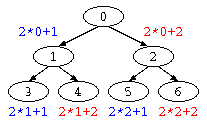
int a[ 7 ] = { 53 , 11 , 86 , 10 , 22 , 65 , 92 } ;
// 2分ヒープを表示
void print_heap( int array[] , int idx , int size ) {
if ( idx < size ) {
// 左の枝を表示
print_heap( array , 2*idx + 1 , size ) ;
// 真ん中の枝を表示
printf( "%d " , array[ idx ] ) ;
// 右の枝を表示
print_heap( array , 2*idx + 2 , size ) ;
}
}
// 2分ヒープから key を検索
int find_heap( int array[] , int idx , int size , int key ) {
while( idx < size ) {
if ( array[ idx ] == key )
return idx ; // 見つかったら配列の番号を返す
else if ( array[ idx ] _____ key ) // 何が入るか考えよう
idx = ________________ ;
else
idx = ________________ ;
}
return -1 ; // 見つからなかったら、-1 を返す
}
int main() {
print_heap( a , 0 , 7 ) ;
if ( find_heap( a , 0 , 7 , 65 ) >= 0 )
printf( "Find!!¥n" ) ;
return 0 ;
}
SQLと結合
前半にSQLの説明の後、後半はSQL実験環境を用いた演習時間とした。
SQLの基礎
前回の講義で、データベースでは、記録されているデータの読み書きは、SQL で行われ、射影・結合・選択を表す処理で構成されることを示した。SQL の機能を理解するために、同じ処理を C 言語で書いたらどうなるのかを示す。
SELECT S.業者番号 -- 必要とされるデータを抽出する射影 --
FROM S -- 複数のテーブルを組合せる結合 --
WHERE S.優良度 >= 20 ; -- 対象となるデータを選び出す選択 --
// 配列の個数を求める #define 文
#define sizeofarray(ARY) (sizeof(ARY) / sizeof(ARY[0]))
// C言語なら... S のデータを構造体宣言で書いてみる。
struct Table_S {
char 業者番号[ 6 ] ; // 当然、C言語では要素名を
char 業者名[ 22 ] ; // 漢字で宣言はできない。
int 優良度 ;
char 所在[ 16 ] ;
} S[] = {
{ "S1" , "ABC社" , 20 , "福井" } ,
:
} ;
// SELECT...をC言語で書いた場合の命令のイメージ
// 結合
for( int i = 0 ; i < sizeofarray( S ) ; i++ ) {
// 選択
if ( S[i].優良度 >= 20 )
// 射影
printf( "%d¥n" , S[i].業者番号 ) ;
}
Sは、テーブル名であり、文脈上対象テーブルが明らかな場合、フィールド名の前の テーブルは省略可能である。
SELECT 業者番号 FROM S WHERE 優良度 >= 20 ;
WHERE 節で記述できる条件式では、= , <>(not equal) , < , > , <= , >= の比較演算子が使える。
# これ以外の演算機能は、次週にて紹介予定。
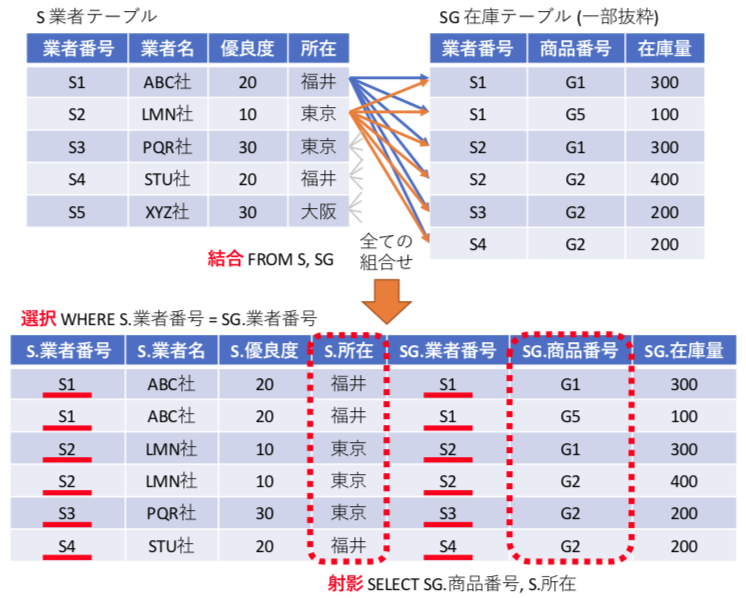
直積と結合処理
ここで、SQLの最も便利な機能は、直積による結合処理。複数の表を組み合わせる処理。単純な表形式の関係データベースで、複雑なデータを表現できる基本機能となっている。
SELECT SG.商品番号 , S.所在 FROM S , SG WHERE SG.業者番号 = S.業者番号
- 実験環境で直積と結合処理(学内のみ)
上記の様に FROM 節に複数のテーブルを書くと、それぞれのテーブルの直積(要素の全ての組み合わせ)を生成する処理が行われる。この機能が結合となる。しかし、これだけでは意味がないので、通常は外部キーが一致するレコードでのみ処理を行うように、WHERE SG.業者番号 = S.業者番号 のような選択を記載する。最後に、結果として欲しいデータを抽出する射影を記載する。
// C言語なら
struct Table_S {
char 業者番号[ 6 ] ;
char 業者名[ 22 ] ;
int 優良度 ;
char 所在[ 16 ] ;
} S[] = {
{ "S1" , "ABC社" , 20 , "福井" } ,
:
} ;
struct Table_SG {
char 業者番号[ 6 ] ;
char 商品番号[ 6 ] ;
int 在庫量 ;
} = SG[] {
{ "S1" , "G1" , 300 } ,
:
} ;
// FROM S
for( int i = 0 ; i < sizeofarray( S ) ; i++ ) {
// FROM SG
for( int j = 0 ; j < sizeofarray( SG ) ; j++ ) {
// WHERE S.業者番号 = SG.業者番号
if ( strcmp( S[i].業者番号 , SG[j].業者番号 ) == 0 ) {
// SELECT SG.商品番号 , S.所在
printf( "%s %s¥n" , SG[j].商品番号 , S[i].所在 ) ;
}
}
}
(1) i,jの2重forループが、FROM節の結合に相当し、(2) ループ内のif文がWHERE節の選択に相当し、(3) printfの表示内容が射影に相当している。
射影の処理では、データの一部分を抽出することから、1件の抽出レコードが同じになることもある。この際の重複したデータを1つにまとめる場合には、DISTINCT を指定する。
SELECT DISTINCT SG.商品番号, S.所在 FROM S, SG WHERE SG.業者番号 = S.業者番号 ;
- 実験環境で結合/重複削除(学内のみ)
上記のプログラムでは、データの検索は単純 for ループで記載しているが、内部で HASH などが使われていると、昇順に処理が行われない場合も多い。出力されるデータの順序を指定したい場合には、ORDER BY … ASC (or DESC) を用いる
SELECT SG.商品番号, S.所在 FROM S, SG WHERE SG.業者番号 = S.業者番号 ORDER BY S.所在 ASC ; -- ASC:昇順 , DESC:降順 --
- 実験環境で結合/並び替え(学内のみ)
表型のデータと串刺し
FROM に記載する直積のための結合では、2つ以上のテーブルを指定しても良い。
SELECT S.業者名, G.商品名, SG.在庫量
FROM S, G, SG
WHERE S.業者番号 = SG.業者番号 -- 外部キー業者番号の対応付け --
AND SG.商品番号 = G.商品番号 -- 外部キー商品番号の対応付け --
// 上記の処理をC言語で書いたら
struct Table_G {
char 商品番号[ 6 ] ;
char 商品名[ 22 ] ;
char 色[ 4 ] ;
int 価格 ;
char 所在[ 12 ] ;
} = G[] = {
{ "G1" , "赤鉛筆" , "青" , 120 , "福井" } ,
:
} ;
// [結合] S,G,SGのすべての組み合わせ
// FROM S -- 結合
for( int i = 0 ; i < sizeofarray( S ) ; i++ ) {
// FROM G -- 結合
for( int j = 0 ; j < sizeofarray( G ) ; j++ ) {
// FROM SG -- 結合
for( int k = 0 ; k < sizeofarray( SG ) ; k++ ) {
// [選択] 条件でレコードを選び出す
// WHERE S.業者番号 = SG.業者番号
// AND SG.商品番号 = G.商品番号
if ( strcmp( S[i].業者番号 , SG[k].業者番号 ) == 0
&& strcmp( SG[k].商品番号 , G[j].商品番号 ) == 0 ) {
// [射影] 使用するフィールドを出力
printf( "%s %s %d\n" ,
S[i].業者名 , G[j].商品名 , SG[k].在庫量 ) ;
}
}
}
}
- 実験環境で結合/3つのTABLEの串刺し(学内のみ)
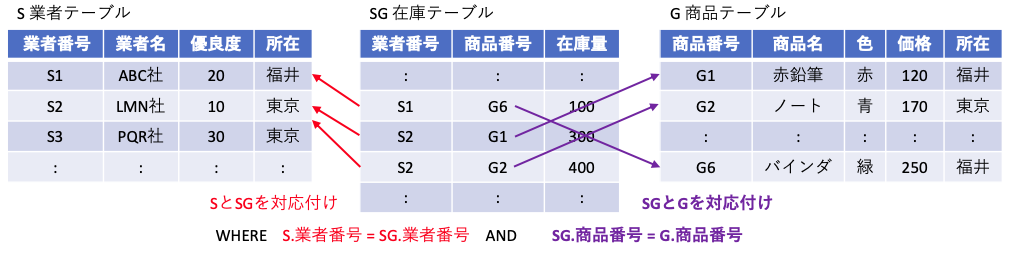ここで結合と選択で実行している内容は、外部キーである業者番号を S から探す、商品番号を G から探している。この、外部キー対応しているものを探すという視点で、上記 C 言語のプログラムを書き換えると、以下のように表せる。
// FROM SG
for( int k = 0 ; k < sizeofarray( SG ) ; k++ ) {
// 外部キー SG.業者番号に対応するものを S から探す
for( int i = 0 ; i < sizeofarray( S ) ; i++ ) {
if ( strcmp( S[i].業者番号 , SG[k].業者番号 ) == 0 ) {
// 外部キー SG.商品番号に対応するものを G から探す
for( int j = 0 ; j < sizeofarray( G ) ; j++ ) {
if ( strcmp(SG[k].商品番号,G[j].商品番号) == 0 ) {
printf( "%s %s %d\n" ,
S[i].業者名,G[j].商品名,SG[k].在庫量 ) ;
}
}
}
}
}
このような、複数の表の実体と関係を対応付けた検索を、データベースの専門の人は「データを串刺しにする」という言い方をすることも多い。
また、SQL では、このようなイメージの繰り返し処理を、数行で分かりやすく記述できている。このプログラム例では、キーに対応するものを単純 for ループで説明しているが、SQL ではプライマリキーなら、B木やハッシュなどを用いた検索が行われるが、SQLの記述するときにはあまり考えなくて良い。
CTFのためのLinuxメモ
- WSL2 のインストール
- Linux環境を使う場合が多いので、WSL2(Windows Subsystem for Linux)をインストールしておきましょう。
ファイル関連
- データ形式 encode / decode
- MIME – メールで、テキストを文字コードを考慮して変換
- base64 – バイナリファイルの変換
- URL encode – WebアクセスでURLに情報を埋め込む
- file – ファイルの種別判断
- zip, unzip, gzip, gunzip – ファイルの圧縮解凍コマンド
- strings – ファイルの中の文字として読める部分の抽出
- more, less, lv – ページャ(ファイルビューア)
- grep – 指定した特定パターンの行だけ出力
- パイプ
- hexcurse – バイナリエディタ
- 4EI学生によると VSCode のプラグインで同等のものがあるらしい。
- big endian, little endian, network byte order
ネットワーク関連
- telnet – 特定のIPアドレス, ポートに接続して通信
- nc – telnet より特化したもの
- nslookup – DNS情報の参照
- dig – nslookup をより汎用にしたもの
- traceroute – ネットワーク経路
- ping – ネットワーク死活確認
- テキストブラウザ
- wget – どちらかというと、ダウンローダ?
- w3m – テキストブラウザ
- curl – 様々なプロトコルで通信できる。
- wireshark – パケットキャプチャ
OS関連
- gdb – デバッガ
- nm – オブジェクトファイルのシンボル情報出力
- objdump – 逆アセンブラ
2分探索木の処理とデータ追加処理
前回の授業では、当初予定に加え、この後に示すデータの追加処理の説明を行った。その代わり、簡単な2分木の演習が抜けていたので少し演習を追加。
2分木の簡単な処理
int count( struct Tree* p ) {
if ( p == NULL )
return 0 ;
else
return 1 + count( p->left )
+ count( p->right ) ;
}
int sum( struct Tree* p ) { // データ合計
if ( p == NULL )
return 0 ;
else
return p->data + sum( p->left )
+ sum( p->right )
}
int max( struct Tree* p ) { // 最大値
if ( p == NULL ) {
return 0 ; // データ件数=0のとき0が最大値でいいのかなぁ？
} else {
while( p->right != NULL )
p = p->right ;
return p->data ;
}
}
int depth( struct Tree* p ) { // 木の深さ
if ( p == NULL ) {
return 0 ;
} else {
int d_l = depth( p->left ) ;
int d_r = depth( p->right ) ;
if ( d_l > d_r )
return d_l + 1 ;
else
return d_r + 1 ;
}
}
int main() {
struct Tree* top = ..... ;
printf( "%d\n" , count( top ) ) ; // 木全体のデータ件数
printf( "%d\n" , sum( top ) ) ; // 木全体のデータ合計
printf( "%d\n" , depth( top ) ) ; // 木全体の最大段数
return 0 ;
}
2分探索木にデータを追加
前回の授業では、データの木構造は、補助関数 tcons() により直接記述していた。実際のプログラムであれば、データに応じて1件づつ木に追加するプログラムが必要となる。この処理は以下のようになるだろう。
struct Tree* top = NULL ;
// 2分探索木にデータを追加する処理
void entry( int d ) {
struct Tree** tail = &top ;
while( *tail != NULL ) {
if ( (*tail)->data == d ) // 同じデータが見つかった
break ;
else if ( (*tail)->data > d )
tail = &( (*tail)->left ) ; // 左の枝に進む
else
tail = &( (*tail)->right ) ; // 右の枝に進む
}
if ( (*tail) == NULL )
*tail = tcons( d , NULL , NULL ) ;
}
int main() {
char buff[ 100 ] ;
int x ;
while( fgets( buff , sizeof( buff ) , stdin ) != NULL )
if ( sscanf( buff , "%d" , &x ) != 1 )
break ;
entry( x ) ;
return 0 ;
}
このプログラムでは、struct Tree** tail というポインタへのポインタ型を用いている。tail が指し示す部分をイメージするための図を以下に示す。
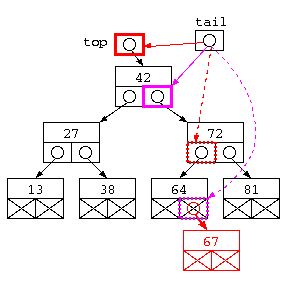
理解確認
- 関数entry() の14行目の if 判定を行う理由を説明せよ。
- 同じく、8行目の tail = &( (*tail)->left ) の式の各部分の型について説明せよ。
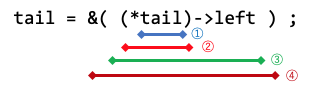
- sscanf() の返り値を 1 と比較している理由を説明せよ。
- entry() でデータを格納する処理時間のオーダを説明せよ。
// 前述プログラムは、データ追加先が大域変数なのがダサい。 // 局所変数で追加処理ができるように、したいけど... void entry( struct Tree* top , int d ) { struct Tree** tail = &top ; while( *tail != NULL ) { : // 上記の entry() と同じとする } void main() { // 追加対象の top は局所変数 struct Tree* top = NULL ; char buff[ 100 ] ; int x ; while( fgets(buff,sizeof(buff),stdin) != NULL ) { if ( sscanf( buff , "%d" , &x ) != 1 ) break ; entry( top , x ) ; } }上記のプログラム↑は動かない。なぜ？
このヒントは、このページ末尾に示す。
演習課題
以下のようなデータを扱う2分探索木のプログラムを作成せよ。以下の箇条書き番号の中から、(出席番号 % 3+1)のデータについてプログラムを作ること。
- 名前(name)と電話番号(phone)
- 名前(name)と誕生日(year,mon,day)
- 名前(name)とメールアドレス(mail)
プログラムは以下の機能を持つこと。
- 1行1件でデータを入力し、2分木に追加できること。
- 全データを昇順(or降順)で表示できること。
- 検索条件を入力し、目的のデータを探せること。
レポートでは、(a)プログラムリスト,(b)その説明,(c)動作検証結果,(d)考察 を記載すること。考察のネタが無い人は、このページの理解確認の内容について記述しても良い。
// プログラムのおおまかな全体像の例
struct Tree {
//
// この部分を考えて
// 以下の例は、名前と電話番号を想定
} ;
struct Tree* top = NULL ;
void tree_entry( char n[] , char ph[] ) {
// n:名前,ph:電話番号 を追加
}
void tree_print( struct Tree* p ) {
// 全データを表示
}
struct Tree* tree_search_by_name( char n[] ) {
// n:名前でデータを探す
}
int main() {
char name[ 20 ] , phone[ 20 ] ;
char buff[ 1000 ] ;
struct Tree* p ;
// データを登録する処理(空行を入力するまで繰り返し)
while( fgets( buff , sizeof( buff ) , stdin ) != NULL ) {
if ( sscanf( buff , "%s%s" , name , phone ) != 2 )
break ; // 入力で、2つの文字列が無い場合はループを抜ける
tree_entry( name , phone ) ;
}
// 全データの表示
tree_print( top ) ;
// データをさがす
while( fgets( buff , sizeof( buff ) , stdin ) != NULL ) {
if ( sscanf( buff , "%s" , name ) != 1 )
break ; // 入力で、1つの文字列が無い場合はループを抜ける
if ( (p = tree_search_by_name( name )) == NULL )
printf( "見つからない¥n" ) ;
else
printf( "%s %s¥n" , p->name , p->phone ) ;
}
return 0 ;
}
動かないプログラムのヒント
// 前述プログラムは、データ追加先が大域変数なのがダサい。
// 局所変数で追加処理ができるように、したいけど...
// ちなみに、こう書くと動く
// Tree*を返すように変更
struct Tree* entry( struct Tree* top , int d ) {
:
// 最初の entry と同じ
:
return top ;
}
void main() {
// 追加対象のポインタ
struct Tree* top = NULL ;
while( ... ) {
:
// entry() の返り値を top に代入
top = entry( top , x ) ;
}
}
fgets()とsscanf()による入力の解説
前述のプログラムの入力では、fgets() と sscanf() による処理を記載した。この関数の組み合わせが初見の人も多いと思うので解説。
// scanf() で苦手なこと -------------------------//
// scanf() のダメな点
// (1) 何も入力しなかったら...という判定が難しい。
// (2) 間違えて、abc みたいに文字を入力したら、
// scanf()では以後の入力ができない。(入力関数に詳しければ別だけどさ)
int x ;
while( scanf( "%d" , &x ) == 1 ) {
entry( x ) ;
}
// scanf() で危険なこと -------------------------//
// 以下の入力プログラムに対して、10文字以上を入力すると危険。
// バッファオーバーフローが発生する。
char name[ 10 ] ;
scanf( "%s" , name ) ;
// 安全な入力 fgets() ---------------------------//
// fgets() は、行末文字"¥n"まで配列 buff[]に読み込む。
// ただし、sizeof(buuf) 文字より長い場合は、途中まで。
char buff[ 100 ] ;
while( fgets( buff , sizeof( buff ) , stdin ) != NULL ) {
// buff を使う処理
}
// 文字列からデータを抜き出す sscanf() -------------//
// sscanf は、文字列の中から、データを抜き出せる。
// 入力が文字列であることを除き、scanf() と同じ。
char str[] = "123 abcde" ;
int x ;
char y[10] ;
sscanf( str , "%d%s" , &x , y ) ;
// x=123 , y="abcde" となる。
// sscanf() の返り値は、2 (2個のフィールドを抜き出せた)
// ただし、Microsoft Visual Studio では、以下のように関数名を読み替えること。
// scanf( ... ) → scanf_s( ... )
// fscanf( ... ) → fscanf_s( ... )
// sscanf( ... ) → sscanf_s( ... )
理解確認
- 標準入力からの1行入力関数 gets() 関数が危険な理由を説明せよ。
SQLの基本
先週の、関係データベースの導入説明を終えて、実際のSQLの説明。
キー
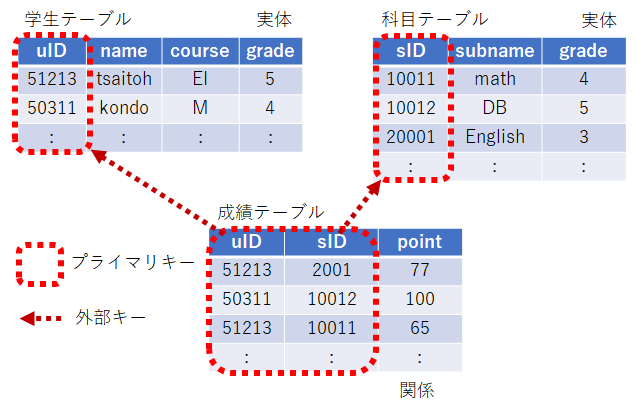
表形式のテーブルの中の各レコードを一意的に指定できるカラムはキーと呼ばれる。
キーは単独であるとは限らず、成績の評価結果であれば、学生と科目をキーとして成績というカラムが１つに絞られる場合もある。
キーのうち、データを一意に識別するためのキーは、プライマリーキーと呼ばれる。以下の例であれば、uID,sID がプライマリーキーである。一方、成績のテーブルでは、uID, sID は、学生,科目のキーとなっている。このようなキーは外部キーと呼ばれる。点数pointは、uID, sID により一意に決まるが、例えば成績の uID に、学生のテーブルに存在しないものが指定されてはいけない。こういった制約は外部キー制約と呼ばれる。
SQLの命令
SQL で使われる命令は、以下のものに分類される。
- データ定義言語 – CREATE, DROP, ALTER 等
- データ操作言語 – INSERT, UPDATE, DELETE, SELECT 等
- データ制御言語 – GRANT, REVOKE 等 (その他トランザクション制御命令など)
create user
データベースを扱う際の create user 文は、DDL(Data Definition Language)で行う。
CREATE USER ユーザ名
IDENTIFIED BY "パスワード"
grant
テーブルに対する権限を与える命令。
GRANT システム権限 TO ユーザ名 データベースシステム全体に関わる権限をユーザに与える。 (例) GRANT execute ON admin.my_package TO saitoh GRANT オブジェクト権限 ON オブジェクト名 TO ユーザ名 作られたテーブルなどのオブジェクトに関する権限を与える。 (例) GRANT select,update,delete,insert ON admin.my_table TO saitoh REVOKE オブジェクト権限 ON オブジェクト名 TO ユーザ名 オブジェクトへの権限を剥奪する。
create table
実際にテーブルを宣言する命令。構造体の宣言みたいなものと捉えると分かりやすい。
CREATE TABLE テーブル名 ( 要素名1 型 , 要素名2 型 ... ) ; PRIMARY KEY 制約 型の後ろに"PRIMARY KEY"をつける、 もしくは、要素列の最後に、PRIMARY KEY(要素名,...)をつける。 これによりKEYに指定した物は、重複した値を格納できない。 型には、以下の様なものがある。(Oracle) CHAR( size) : 固定長文字列 / NCHAR国際文字 VARCHAR2( size ) : 可変長文字列 / NVARCHAR2... NUMBER(桁) :指定 桁数を扱える数 BINARY_FLOAT / BINARY_DOUBLE : 浮動小数点(float / double) DATE : 日付(年月日時分秒) SQLiteでの型 INTEGER : int型 REAL : float/double型 TEXT : 可変長文字列型 BLOB : 大きいバイナリデータ DROP TABLE テーブル名 テーブルを削除する命令
insert,update,delete
指定したテーブルに新しいデータを登録,更新,削除する命令
INSERT INTO テーブル名 ( 要素名,... ) VALUES ( 値,... ) ; 要素に対応する値をそれぞれ代入する。 UPDATE テーブル名 SET 要素名=値 WHERE 条件 指定した条件の列の値を更新する。 DELETE FROM テーブル名 WHERE 条件 指定した条件の列を削除する。
select
データ問い合わせは、select文を用いる、 select文は、(1)必要なカラムを指定する射影、(2)指定条件にあうレコードを指定する選択、 (3)複数のテーブルの直積を処理する結合から構成される。
SELECT 射影 FROM 結合 WHERE 選択 (例) SELECT S.業者番号 FROM S WHERE S.優良度 > 30 ;
理解確認
- キー・プライマリキー・外部キーについて説明せよ。
- 上記説明中の、科目テーブルにふさわしい create table 文を示せ。
- select文における、射影,結合,選択について説明せよ。
CTF問題とセキュリティ(4年実験)
この実験では、セキュリティコンテストのCTF問題(Capture The Flag競技)について、インターネットの仕組みを理解し、その問題の解き方を考え、新しく自分自身でCTF問題を作ってもらいます。
日程
実験は、4週にわたり、以下の日程で行います。
| 週 | 内容 |
| 1 | (前半)暗号・ファイル・Web |
| 2 | |
| 3 | (後半) プログラム作成・インターネット・OS |
| 4 |
前半・後半でそれぞれ、問題例(もしくは自分で見つけたCTF問題)の1つの説明と、自作の問題を新しく作り説明をしてください。
提出物
- 実験の目的
- 問題例(or 自分で見つけたCTF問題)を1つ選び
- 前半・後半それぞれについて
- その問題が情報セキュリティにどう関係しているのか
- 問題の解き方のしくみと解説
- 自作問題について
- 前半・後半それぞれ
- その問題が情報セキュリティにどう関係しているのか
- 問題の解き方、問題の作り方
- しくみと解説
- 提出先はこちらのTeams共有フォルダに。
2分探索木
配列やリスト構造のデータの中から、目的となるデータを探す場合、配列であれば2分探索法が用いられる。これにより、配列の中からデータを探す処理は、O(log N)となる。(ただし事前にデータが昇順に並んでいる必要あり)
// 2分探索法
int array[ 8 ] = { 11, 13 , 27, 38, 42, 64, 72 , 81 } ;
int bin_search( int a[] , int key , int L , int R ) {
// Lは、範囲の左端
// Rは、範囲の右端+1 (注意!!)
while( R > L ) {
int m = (L + R) / 2 ;
if ( a[m] == key )
return key ;
else if ( a[m] > key )
R = m ;
else
L = m + 1 ;
}
return -1 ; // 見つからなかった
}
void main() {
printf( "%d¥n" , bin_search( array , 0 , 8 ) ) ;
}
一方、リスト構造ではデータ列の真ん中のデータを取り出すには、先頭からアクセスするしかないのでO(N)の処理時間がかかり、極めて効率が悪い。リスト構造のようにデータの追加が簡単な特徴をもったまま、もっとデータを高速に探すことはできないものか？
2分探索木
ここで、データを探すための効率の良い方法として、2分探索木(2分木)がある。以下の木のデータでは、分離する部分に1つのデータと、左の枝(下図赤)と右の枝(下図青)がある。
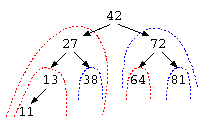
この枝の特徴は何だろうか？この枝では、中央のデータ例えば42の左の枝には、42未満の数字の枝葉が繋がっている。同じように、右の枝には、42より大きな数字の枝葉が繋がっている。この構造であれば、64を探したいなら、42より大きい→右の枝、72より小さい→左の枝、64が見つかった…と、いう風にデータを探すことができる。
特徴としては、1回の比較毎にデータ件数は、(N-1)/2件に減っていく。よって、この方法であれば、O(log N)での検索が可能となる。これを2分探索木とよぶ。
このデータ構造をプログラムで書いてみよう。
struct Tree {
struct Tree* left ;
int data ;
struct Tree* right ;
} ;
// 2分木を作る補助関数
struct Tree* tcons( struct Tree* L ,
int d ,
struct Tree* R ) {
struct Tree* n = (struct Tree*)malloc(
sizeof( struct Tree ) ) ;
if ( n != NULL ) { /* (A) */
n->left = L ;
n->data = d ;
n->right = R ;
}
return n ;
}
// 2分探索木よりデータを探す
int tree_search( struct List* p , int key ) {
while( p != NULL ) {
if ( p->data == key )
return key ;
else if ( p->data > key )
p = p->left ;
else
p = p->right ;
}
return -1 ; // 見つからなかった
}
struct Tree* top = NULL ;
void main() {
// 木構造をtcons()を使って直接生成 (B)
top = tcons( tcons( tcons( NULL , 13 , NULL ) ,
27 ,
tcons( NULL , 38 , NULL ) ) ,
42 ,
tcons( tcons( NULL , 64 , NULL ) ,
72 ,
tcons( NULL , 81 , NULL ) ) ) ;
printf( "%d¥n" , tree_search( top , 64 ) ) ;
}
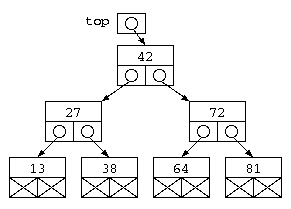
この方式の注目すべき点は、struct Tree {…} で宣言しているデータ構造は、2つのポインタと1つのデータを持つという点では、双方向リストとまるっきり同じである。データ構造の特徴の使い方が違うだけである。
理解度確認
- 上記プログラム中の、補助関数tcons() の(A)の部分 “if ( n != NULL )…” の判定が必要な理由を答えよ。
- 同じくmain() の (B) の部分 “top = tcons(…)” において、末端部に NULL を入れる理由を答えよ。
2分木に対する処理
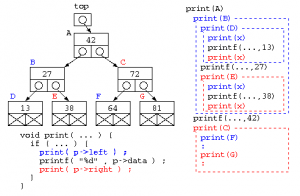
2分探索木に対する簡単な処理を記述してみよう。
// データを探す
int search( struct Tree* p , int key ) {
// 見つかったらその値、見つからないと-1
while( p != NULL ) {
if ( p->data == key )
return key ;
else if ( p->data > key )
p = p->left ;
else
p = p->right ;
}
return -1 ;
}
// データを全表示
void print( struct Tree* p ) {
if ( p != NULL ) {
print( p->left ) ;
printf( "%d¥n" , p->data ) ;
print( p->right ) ;
}
}
// データ件数を求める
int count( struct Tree* p ) {
if ( p == NULL )
return 0 ;
else
return 1
+ count( p->left )
+ count( p->right ) ;
}
// データの合計を求める
int sum( struct Tree* p ) {
if ( p == NULL )
return 0 ;
else
return p->data
+ count( p->left )
+ count( p->right ) ;
}
// データの最大値
int max( struct Tree* p ) {
while( p->right != NULL )
p = p->right ;
return p->data ;
}
これらの関数では、木構造の全てに対する処理を実行する場合には、再帰呼び出しが必要となる。
データベースの用語など
データベースの機能
データベースを考える時、利用者の視点で分類すると、(1) データベースの管理者(データベース全体の管理)、(2) 応用プログラマ(SQLなどを使って目的のアプリケーションに合わせた処理を行う)、(3) エンドユーザ(データベース処理の専門家でなく、DBシステムのGUIを使ってデータベースを操作する)となる。
データベース管理システム(DBMS)では、データとプログラムを分離してプログラムを書けるように、データ操作言語(SQL)で記述する。
また、データは独立して扱えるようにすることで、データへの物理的なアクセス方法があっても、プログラムの変更が不要となるようにします。
データベースは、利用者から頻繁に不定期にアクセスされる。このため、データの一貫性が重要となる。これらを満たすためには、(a) データの正当性の確認、(b) 同時実行制御(排他制御)、(c) 障害回復の機能が重要となる。
これ以外にも、データベースからデータを高速に扱えるためには、検索キーに応じてインデックスファイルを管理してくれる機能や、データベースをネットワーク越しに使える機能などが求められる。
データベースに対する視点
実体のデータをそれぞれの利用者からデータベースを記述したものはスキーマと呼ばれる。そのスキーマも3つに分けられ、これを3層スキーマアーキテクチャと呼ぶ。
- 外部スキーマ – エンドユーザからどんなデータに見えるのか
- 概念スキーマ – 応用プログラマからは、どのような表の組み合わせで見えるのか、表の中身はどのようなものなのか。
- 内部スキーマ – データベース管理者からみて、表の中身は、どのようなファイル名でどのような形式でどう保存されているのか
データモデル
データを表現するモデルには、いくつかのモデルがある。
- 階層型データモデル – 木構造で枝葉に行くにつれて細かい内容
- ユーザ情報を扱うLDAP(Light Weight Directory Access Protocol)は、階層モデルの例
- ディレクトリサービス: コンピュータのリソースの属性や情報のデータベース
- ネットワーク型モデル – データの一部が他のデータ構造と関係している。
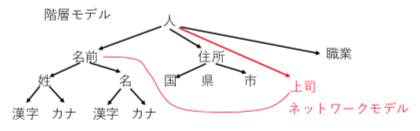
- 関係モデル – すべてを表形式で表す。
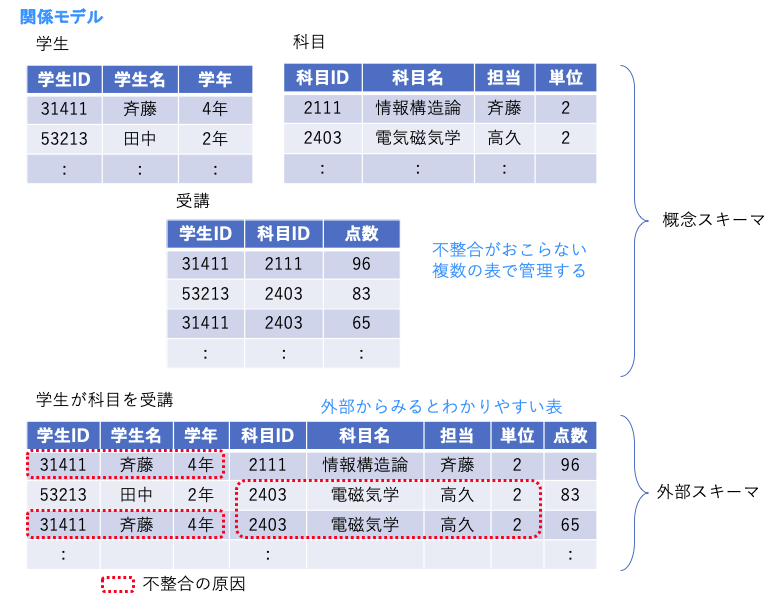
データベースの基礎
データベースは、1970年頃に、E.F.コッド博士によりデータベースのための数学的な理論が確立された。
- 集合 A, B – 様々なデータ
- 直積 A✕B = { (x,y) | x∈A , y∈B } 集合A,Bのすべての組み合わせ
- 関係 R(A,B) すべての組み合わせのうち、関係があるもの。直積A,Bの部分集合
例えば、A={ s,t,u } , B={ p,q } (定義域) なら、
A✕B = { (s,p) , (s,q) , (t,p) , (t,q) , (u,p) , (u,q) }
このうち、Aが名前(sさん,tさん,uさん)、Bが性別(p=男性,q=女性)を表すなら、
R(A,B) = { (s,p) , (t,q) , (u,p) } (例)
(例)：(sさん,男性) , (tさん,女性) , (uさん,男性)
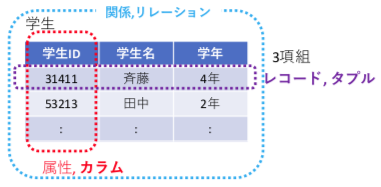
理解確認
- データベースにおける3層スキーマアーキテクチャについて説明せよ
- 集合A,Bが与えられた時、関係R(A,B) はどのようなものか、数学定義や実例をあげて説明せよ。