DCON2021で福井高専チーム優勝
4/17(土) に開催された 第2回全国高等専門学校 ディープラーニングコンテスト2021 にて、福井高専のプログラミング研究会チームの D-ON にて優勝しました。
「全国高等専門学校ディープラーニングコンテスト(DCON)」は高専生が日頃培った<ものづくりの技術>と人工知能(AI)分野の重要技術<ディープラーニング>を活用した作品を制作し、生み出される<事業性>を企業評価額で競うコンテストです。
D-ON
D-ON / トンネルや橋の点検のために行われる打音検査を低コストで実現するためのシステム。「打音検査が必要なトンネルや橋は日本で約80万以上あるが、熟練の点検員が検査を行う必要があるため、コストが掛かっている」という課題の解決を目指しシステムが作られました。
プログラミング研究会(4EI 前川, 小川, 指導:村田) (写真はDCON2021 HPより引用)
DCON2021 Twitter のページより引用
値渡しとポインタ渡し
C言語をあまりやっていない学科の人向けのC言語の基礎として、関数との値渡し, ポインタ渡しについて説明する。ただし、参照渡しについては電子情報の授業でも細かく扱っていない内容なので電子情報系学生も要注意。
オブジェクト指向のプログラムでは、構造体のポインタ渡し(というよりは参照渡し)を多用するが、その基本となる関数との値の受け渡しの理解のため、以下に値渡し・ポインタ渡し・参照渡しについて説明する。
ポインタと引数
値渡し
// 値渡しのプログラム
void foo( int x ) { // x は局所変数(仮引数は呼出時に
// 対応する実引数で初期化される。
x++ ;
printf( "%d¥n" , x ) ;
}
int main() {
int a = 123 ;
foo( a ) ; // 124
// 処理後も main::a は 123 のまま。
foo( a ) ; // 124
return 0 ;
}
このプログラムでは、aの値は変化せずに、124,124 が表示される。
でも、プログラムによっては、124,125 と変化して欲しい場合もある。
どのように記述すべきだろうか?
// 大域変数を使う場合
int x ;
void foo() {
x++ ;
printf( "%d¥n" , x ) ;
}
int main() {
x = 123 ;
foo() ; // 124
foo() ; // 125
return 0 ;
}
しかし、このプログラムは大域変数を使うために、間違いを引き起こしやすい。
// 大域変数が原因で予想外の挙動をしめす簡単な例
int i ;
void foo() {
for( i = 0 ; i < 2 ; i++ )
printf( "A" ) ;
}
int main() {
for( i = 0 ; i < 3 ; i++ ) // このプログラムでは、AA AA AA と
foo() ; // 表示されない。
return 0 ;
}
ポインタ渡し
C言語で引数を通して、呼び出し側の値を変化して欲しい場合は、変更して欲しい変数のアドレスを渡し、関数側では、ポインタ変数を使って受け取った変数のアドレスの示す場所の値を操作する。
// ポインタ渡しのプログラム
void foo( int* p ) { // p はポインタ
(*p)++ ;
printf( "%d¥n" , *p ) ;
}
int main() {
int a = 123 ;
foo( &a ) ; // 124
// 処理後 main::a は 124 に増えている。
foo( &a ) ; // 124
return 0 ; // さらに125と増える
}
ポインタを利用して引数に副作用を与える方法は、ポインタを正しく理解していないプログラマーでは、危険な操作となる。C++では、ポインタ渡しを極力使わないようにするために、参照渡しを利用する。ただし、ポインタ渡しも参照渡しも、機械語レベルでは同じ処理にすぎない。
参照渡し
// ポインタ渡しのプログラム void foo( int& x ) { // xは参照 x++ ; printf( "%d¥n" , x ) ; } int main() { int a = 123 ; foo( a ) ; // 124 // 処理後 main::a は 124 に増えている。 foo( a ) ; // 124 return 0 ; // さらに125と増える。 }
構造体のポインタ渡し
ここまでの説明を踏まえ、構造体を使ったプログラムでは、構造体のポインタ渡しが一般的である。以下に、名前と年齢のデータを扱うプログラムを示す。
// 構造体のポインタ渡しのプログラム
struct Person {
int name[ 20 ] ;
int age ;
} ;
// 構造体にデータを代入するための関数
void set_Person( struct Person* p , char nm[] , int ag ) {
// ポインタ参照で書くと以下の通り
strcpy( (*p).name , nm ) ;
(*p).age = ag ;
// アロー演算子を使うとシンプルに書ける。
// strcpy( p->name , nm ) ;
// p->age = ag ;
}
// 構造体のデータを表示するための関数
void print_Person( struct Person* p ) {
printf( "%s %d¥n" , p->name , p->age ) ;
}
// 関数名さえ処理の意図がつたわる名前を使えば、
// 値をセットして、表示する...ぐらいは一目瞭然。
// 構造体の中身を知らなくても、関数の中身を知らなくても、
// やりたいことは伝わる。...隠蔽化
int main() {
struct Person tsaitoh ;
// tsaitohに set して、
set_Person( &tsaitoh , "t-saitoh" , 55 ) ;
// tsaitohを print する。
print_Person( &tsaitoh ) ;
return 0 ;
}
このプログラムでは、main() の部分だけを見ると、tsaitoh という Person というデータがあり、set_Person() で値をセットして、print_Person() で値を出力するという雰囲気は伝わる。
この main() であれば、Person の name が文字配列とか age が int 型といった情報は知らなくても使える。(データ構造の隠蔽化)
また、set_Person() や print_Person() もどんな関数を使って表示しているのかも知らなくてもいい。(手続きの隠蔽化)
これにより、Person というデータ構造やそれを扱う処理の中身を設計する人と、Person というデータを使う人でプログラム開発の分業ができる。さらに、プログラムで不具合があったときは、Personの内部が悪いのか、使い方が悪いのかの原因の切り分けも明確になる。
オブジェクト指向プログラミングに書き換え
// 構造体のポインタ渡しのプログラム
class Person {
private:
int name[ 20 ] ;
int age ;
public:
void set( char nm[] , int ag ) {
strcpy( name , nm ) ;
age = ag ;
}
void print() {
printf( "%s %d\n" , name , age ) ;
}
} ; // ← この行の「;」に要注意
int main() {
Person tsaitoh ;
// tsaitohに set して、
tsaitoh.set( "t-saitoh" , 55 ) ;
// tsaitohを print する。
tsaitoh.print() ;
return 0 ;
}
繰り返し処理と処理時間の見積もり
単純サーチの処理時間
ここで、プログラムの実行時間を細かく分析してみる。
// ((case-1))
// 単純サーチ O(N)
#define SIZE 1024
int a[ SIZE ] ; // 配列
int size ; // 実際のデータ数(Nとする)
int key ; // 探すデータ
for( int i = 0 ; i < size ; i++ )
if ( a[i] == key )
break ;
例えばこの 単純サーチをフローチャートで表せば、以下のように表せるだろう。フローチャートの各部の実行回数は、途中で見つかる場合があるので、最小の場合・最大の場合を考え平均をとってみる。また、その1つ1つの処理は、コンピュータで機械語で動くわけだから、処理時間を要する。この時間を とする。
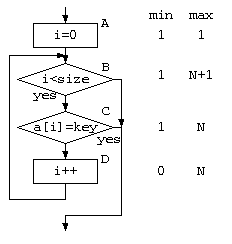
この検索処理全体の時間 を考えると、平均時間とすれば、以下のように表せるだろう。
ここで例題
この単純サーチのプログラムを動かしてみたら、N=1000で、5μ秒かかったとする。では、N=10000であれば、何秒かかるだろうか?
感のいい学生であれば、直感的に 50μ秒 と答えるだろうが、では、Tβ,Tα は何秒だったのだろうか? 上記のT(N)=Tα+N ✕ Tβ に当てはめると、N=1000,T(N)=5μ秒の条件では、連立方程式は解けない。
ここで一番のポイントは、データ処理では N が小さな値の場合はあまり考えない。N が巨大な値であれば、Tαは、1000Tβに比べれば微々たる値という点である。よって
で考えれば良い。これであれば、T(1000)=5μ秒=Tβ×1000 よって、Tβ=5n秒となる。この結果、T(10000)=Tβ×10000=50μ秒 となる。
2分探索法と処理時間
次に、単純サーチよりは、速く・プログラムとしては難しくなった方法として、2分探索法の処理時間を考える。
// ((case-2))
// 2分探索法
int L=0 , R=size ; // プログラムは複雑になった
while( L != R ) {
int M = (L + R) / 2 ;
if ( a[M] == key )
break ;
else if ( a[M] < key )
L = M + 1 ;
else
R = M ;
}
このプログラムでは、1回のループ毎に対象となるデータ件数は、となる。説明を簡単にするために1回毎にN/2件となると考えれば、M回ループ後は、
件となる。データ件数が1件になれば、データは必ず見つかることから、以下の式が成り立つ。
…両辺のlogをとる
2分探索は、繰り返し処理であるから、処理時間は、
ここで、本来なら log の底は2であるが、後の見積もりの例では、問題に応じて底変換の公式で係数が出てくるが、これはTβに含めて考えればいい。
単純なソート(選択法)の処理時間
次に、並べ替え処理の処理時間について考える。
単純な並べ替えアルゴリズムとしてはバブルソートなどもあるが、2重ループの内側のループ回数がデータによって変わるので、選択法で考える。
int a[ 1000 ] = { 対象となるデータ } ;
int size = N ;
for( int i = 0 ; i < size - 1 ; i++ ) {
int tmp ;
// i..size-1 の範囲で一番大きいデータの場所を探す
int m = i ;
for( int j = i + 1 ; j < size ; j++ ) {
if ( a[j] > a[m] )
m = j ;
}
// 一番大きいデータを先頭に移動
tmp = a[i] ;
a[i] = a[m] ;
a[m] = tmp ;
}
このプログラムの処理時間T(N)は…
… i=0の時
… i=1の時
:
… i=N-1の時
…(参考 数列の和の公式)
となる。
オーダー記法
ここまでのアルゴリズムをまとめると以下の表のようになる。ここで処理時間に大きく影響する部分は、最後の項の部分であり、特にその項の係数は、コンピュータの処理性能に影響を受けるが、アルゴリズムの優劣を考える場合は、それぞれ、
の部分の方が重要である。
| 単純サーチ | |
| 2分探索法 | |
| 最大選択法 |
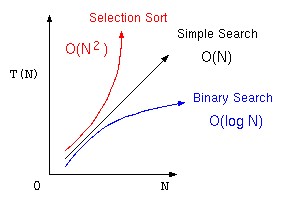
そこで、アルゴリズムの優劣を議論する場合は、この処理時間の見積もりに最も影響する項で、コンピュータの性能によって決まる係数を除いた部分を抽出した式で表現する。これをオーダー記法と言う。
| 単純サーチ | オーダーNのアルゴリズム | |
| 2分探索法 | オーダー log N のアルゴリズム | |
| 最大選択法 | オーダー N2 のアルゴリズム |
練習問題
- ある処理のデータ数Nに対する処理時間が、
であった場合、オーダー記法で書くとどうなるか?
- コンピュータで2分探索法で、データ100件で10[μsec]かかったとする。
データ10000件なら何[sec]かかるか?
(ヒント: 底変換の公式) の処理時間を要するアルゴリズムを、オーダー記法で書くとどうなるか?また、このようなアルゴリズムの例を答えよ。
の処理時間を要するアルゴリズムを、オーダー記法で書くとどうなるか?
(ヒント: ロピタルの定理)
- 2と4の解説
- 1は、N→∞において、N2<<2Nなので、O(2N) 。厳密に回答するなら、練習問題4と同様の説明を行う。
- 3は、O(1)。誤答の例:O(0)と書いちゃうと、T(N)=Tα×0=0になってしまう。事例は、電話番号を、巨大配列の”電話番号”番目の場所に記憶するといった方法。(これはハッシュ法で改めて講義予定)
再帰呼び出しの予習
次の講義の基礎を確認という意味で、再帰呼出しと簡単な処理の例を説明する。
最初に定番の階乗(fact)

次に、フィボナッチ数列の場合

次の講義への導入問題
ここで示す導入問題をすべて答えるには、若干の予習が必要です。まずはどういう考え方をすれば解けるかな…を考えてみてください。
- fact(N)の処理時間を、
のような式で表現し、処理時間をオーダ記法で答えよ。
- 以下のプログラムの実行結果を答えよ。また、関数sum()の処理時間を対象となるデータ件数N=R–Lを用いて
のような式で表現せよ。
int a[] = { 1 , 5 , 8 , 9 , 2 , 3 , 4 , 7 } ;
int sum( int a[] , int L , int R ) {
if ( R-L == 1 ) {
return a[L] ;
} else {
int M = (L + R) / 2 ;
return sum( a , L , M ) + sum( a , M , R ) ;
}
}
int main() {
printf( "%d¥n" , sum( a , 0 , 8 ) ) ;
return 0 ;
}
情報構造論2021ガイダンス
基本的なガイダンス
情報構造論のシラバスを、ここに示す。プログラムを作成する上で、どのような考え方で作れば処理速度が速いのかを議論する。基本的に、4回のテストのたびに、レポート課題を実施する。各テスト毎の評価は、テスト素点と、「テスト素点×60%+レポート評価×40%」の良い方とする。テストに自信のない人は、レポート課題をきちんと提出すること。ただし、今後の休講などの影響で評価方法は随時変更を行う。
プログラムを評価する3つのポイント
まずは以下を読む前に、質問。
- あなたが良いプログラムを作るために何を考えて作りますか? ※1
- ここまでの段階で3つの要点を考えメモしておいてください。
- ガイダンス最初のレポートに使います。
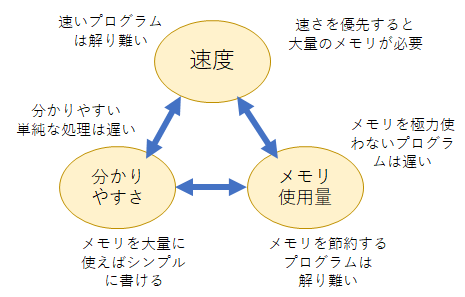
具体的な言葉で要点を考えると、いろいろなものがでてくるだろうが、端的なポイントにまとめると、次の3つに分類できるはずである。
- プログラムの速度
- プログラムのわかり易さ
- メモリの使用量
プログラムを作る場合、この3要素がトレードオフの関係にある。プログラムの速度を優先すると、プログラムが分かり難くなったり、メモリを大量浪費するものだったりする。
メモリの使用量の影響
メモリを大量に使用すると、どういった影響がでるのか? OSの機能を知らないと、メモリ(主記憶)を使い果たしたら、プログラムが動かないと思うかもしれないけど、最近のOSは仮想メモリ機能があるため、主記憶がメモリが足りなければ待機状態のプロセスのメモリを補助記憶に保存することで、プログラムを動かすことはできる。(仮想記憶)
しかし、プロセスが切り替わる度に、補助記憶への読み書きが発生するため、処理性能は低下する。(スワッピング)
ソフトウェアとアルゴリズムとプログラム
用語として、ソフトウェア、アルゴリズム、プログラムという表現があるが、この違いは何か?
- アルゴリズム – 計算手順の考え方。
- プログラム – アルゴリズムを特定のプログラム言語によって記述したもの。
- ソフトウェア – プログラムと、その処理に必要なデータ。(日本語を変換するプログラムは、日本語の辞書データが無いと動かない)
- パラダイム – プログラムをどう表現すると分かりやすいか?
トレードオフ関係をプログラムで確認
例えば、配列の中から、目的データを探すプログラムの場合、最も簡単なプログラムは以下の方法であろう。
// ((case-1))
// 単純サーチ O(N)
#define SIZE 1024
int a[ SIZE ] ; // 配列
int size ; // 実際のデータ数(Nとする)
int key ; // 探すデータ
for( int i = 0 ; i < size ; i++ )
if ( a[i] == key )
break ;
しかし、もっと早く探したいのであれば、2分探索法を用いるだろう。でも、このプログラムは、case-1 のプログラムよりは分かり難い。(速度⇔わかり易さ)
// ((case-2))
// 2分探索法
int L=0 , R=size ; // プログラムは複雑になった
while( L != R ) {
int M = (L + R) / 2 ;
if ( a[M] == key )
break ;
else if ( a[M] < key )
L = M + 1 ;
else
R = M ;
}
でももっと速いプログラムとしたければ、大量のメモリを使えば一発でデータを探せる。(速度⇔メモリ使用量)
// ((case-3)) // 添字がデータ O(1) // 探すデータが電話番号 272925 のような 6 桁ならば int a[ 1000000 ] ; a[ 272925 ] = 272925 ; // 処理速度はクソ速いけど、メモリは大量消費
良いプログラムを作るとは
プログラムを作る時には、メモリが大量に使えるのなら、速いものを使えばいい。だけど実際には、そのシステムには限られた予算があるだろう。
実際には、限られた予算からメモリやCPUが決まり、その会社の人員やら経験やらでプログラム開発に使える時間がきまる。プログラムをデザインするとは、限られた条件の中で、適切な速度のコンピュータ、適切な量のメモリでコンピュータを用意し、限られた納期の中でシステムを完成させることである。
皆さんも、ゲームを買った時、処理速度が遅くてキャラクターがカクカク動いたら幻滅するでしょ?ゲームがバグですぐに変な動きしたらキレるでしょ!発売日の予定どおりに買えなかったらさみしいでしょ!!プログラムがでかすぎてローディングに時間がかかったら、寝ちゃうでしょ!!!
組み合わせ問題の解き方(予備実験)
プログラミングコンテストの競技部門では、パズルのような組み合わせ問題が 出題されることが多い。また、課題部門や自由部門であっても、複数の条件の組み合わせの中から最良のものを選ぶといった処理も求められる。そこで、この予備実験では、きわめて単純なパズル問題(組み合わせ問題) のプログラムについて扱う。
組み合わせ問題の基礎
簡単な問題として「100未満の整数の値を3つ選び、その値を辺の長さとした場合、 直角三角形となるものをすべて表示する。」について考える。
一番簡単な方法は、以下となるであろう。
#include <stdio.h>
#include <math.h>
#include <time.h>
// 整数比の直角三角形の一覧を求める。
void integer_triangle( int n ) {
for( int a = 1 ; a < n ; a++ ) {
for( int b = 1 ; b < n ; b++ ) {
// 一番ダサい方法
for( int c = 1 ; c < n ; c++ ) {
if ( a*a + b*b == c*c ) {
printf( "%d %d %d\n" , a , b , c ) ;
}
}
}
}
}
int main() {
integer_triangle( 100 ) ;
return 0 ;
}
しかしこのプログラムの欠点としては、100×100×100回のループで無駄な処理が多い。
4EIの情報構造論で説明するネタだけど、こういうアルゴリズムは、O(N3) のアルゴリズムという。
ループ回数を減らすだけなら、最も内側の処理を、計算で整数値か確認すればいい。
O(N2) のアルゴリズム
void integer_triangle( int n ) {
for( int a = 1 ; a < n ; a++ ) {
for( int b = 1 ; b < n ; b++ ) {
// ココも改良できるよね?
int d = a*a + b*b ;
int c = (int)sqrt( d ) ;
// 斜辺Cの整数値を求め、改めて確認する。
if ( c*c == d ) {
printf( "%d %d %d\n" , a , b , c ) ;
}
}
}
}
(1) 計算誤差の問題を考えてみよう。
たとえば、3:4:5の直角三角形で、3*3+4*4 = 25 だが、sqrt(25)は実数で計算するから、 計算誤差で4.99999で求まったらどうなるだろうか?
1~100までの数値で、”int c = sqrt( (double)(i*i) ) ;” を計算してみて、 異なる値が求まることはあるか? 多少の計算誤差があっても正しく処理が行われるにはどうすればいいか、考えてみよう。
(2) 無駄な答えについて考えてみよう。
このプログラムの答えでは、簡単な整数比の答えの「整数倍の答え」も表示されてしまう。 たとえば、(3:4:5)の答えのほかに、(6:8:10)も表示される。 こういった答えを表示しないようにするにはどうすればよいか?
また、この2つのプログラムの処理時間を実際に比べてみる。
#include <stdio.h>
#include <time.h>
int main() {
time_t start , end ;
// time() 関数は、秒数しか求まらないので、
// あえて処理を1000回繰り返し、数秒かかる処理にする。
start = time( NULL ) ;
for( int i = 0 ; i < 1000 ; i++ ) {
// ただし、関数内のprintfをコメントアウトしておくこと
integer_triangle( 100 ) ;
}
end = time( NULL ) ;
printf( "%lf\n" , difftime( end , start ) ) ;
return 0 ;
}
再帰プログラミング
組み合わせ問題では、forループの多重の入れ子で問題を解けない場合が多い。 (書けないことはないけど無駄なループで処理が遅くなるか、入れ子段数が可変にできない。)
こういった場合には、再帰プログラミングがよく利用される。 もっとも簡単な再帰の例として、階乗のプログラムを考える。 通常であれば、以下のような for ループで記述することになるだろう。
// 階乗の計算
int fact( int x )
{ // ループ
int f = 1 ;
for( int i = 2 ; i <= x ; i++ )
f = f * i ;
return f ;
}
再帰呼び出しでは、関数の処理の中に、自分自身の関数呼び出しが含まれる。 また、無限に自分自身を呼び出したら処理が止まらないので、 問題を一つ小さくして、これ以上小さくできないときは処理を止めるように記述する。
int fact( int x )
{ // 再帰呼び出し
if ( x <= 1 )
return 1 ;
else
return x * fact( x - 1 ) ;
}
ここ以降は、指定長さを指定辺の組み合わせで作る課題と、後に述べるFlood-fill 課題の選択とする。
指定長を指定辺の組み合わせで作る(テーマ1)
再帰を使った簡単なパズル問題として、以下のプログラムを作成したい。
配列の中に、複数の辺の長さが入っている。これを組み合わせて指定した長さを作れ。 使用する辺はできるだけ少ない方がよい。
int a[] = { 4 , 5 , 2 , 1 , 3 , 7 } ;
(例) 辺の長さ10を作るには、(5,4,1)とか(7,3)などが考えられる。
これは、ナップサック問題の基本問題で、容量の決まったナップサックに最大量入れる組合せを求めるのと同じである。
このプログラムを解くには…
10 を [4,5,2,1,3,7] で作るには... (0) 6=10-4 を [4|5,2,1,3,7]で作る。 (1) 5=10-5 を [5|4,2,1,3,7]で作る。 (2) 8=10-2 を [2|5,4,1,3,7]で作る。 (3) 9=10-1 を [1|5,2,4,3,7]で作る。 (4) 7=10-3 を [3|5,2,1,4,7]で作る。 (5) 3=10-7 を [7|5,2,1,3,4]で作る。
そこで、ここまでの考えを、以下のようなプログラムで記述してみる。
# まだ再起呼び出しにはしていない。
// 指定されたデータを入れ替える。
void swap( int*a , int*b )
{ int x = *a ;
*a = *b ;
*b = x ;
}
void check( int array[] , int size , int len , int n )
{
// array[] 配列
// size 配列サイズ
// len 作りたい長さ
// n 使った個数
for( int i = n ; i < size ; i++ ) {
// i番目を先頭に...
swap( &array[ n ] , &array[ i ] ) ;
printf( "check( array , %d , %d , %d )\n" ,
size , len - array[ n ] , n+1 ) ;
// 最初のswapでの変更を元に戻す。
swap( &array[ i ] , &array[ n ] ) ;
}
}
int main() {
int a[] = { 4 , 5 , 2 , 1 , 3 , 7 } ;
check( a , 6 , 10 , 0 ) ;
}
(1) これを再帰呼び出しにしてみよう。どう書けばいい?
void check( int array[] , int size , int len , int n )
{
// array[] 配列
// size 配列サイズ
// len 作りたい長さ
// n 使った個数
if ( len < 0 ) {
// 指定した丁度の長さを作れなかった。
;
} else if ( len == 0 ) {
// 指定した長さを作れたので答えを表示。
for( int i = 0 ; i < n ; i++ ) {
printf( "%d " , array[ i ] ) ;
}
printf( "\n" ) ;
} else {
// 問題を一つ小さくして再帰。
for( int i = n ; i < size ; i++ ) {
swap( &array[ n ] , &array[ i ] ) ;
printf( "check( array , %d , %d , %d )\n" ,
size , len - array[ n ] , n+1 ) ;
check( array , size , len - array[ n ] , n + 1 ) ;
swap( &array[ i ] , &array[ n ] ) ;
}
}
}
(2) 少ない組み合わせの方がポイントが高い場合には、プログラムをどう変更する?
(3) 答えが1つだけで良い場合は、プログラムをどう変更する?
(4) このプログラムでは、冗長な答えがあるか?ないか?検討せよ。
(5) 前設問の整数比直角三角形のプログラムで、冗長な答えを削除するプログラムを作成せよ。
# レポートでは、(2),(3),(4)を検討した結果を実験すること。(5)までチャレンジした人は(2),(3),(4)の説明は簡単に記載するだけで良い。
別解
この問題の解き方には、もっとシンプルな書き方がある。2進数の各bitを、j番目の長さを使うか使わないかを表すこととする。
例えば、j=1番目,3番目を使うというのを、000101)2=5で表すこととする。すべての長さを使うのであれば、111111)2=63 で表す。この2進数を1から63まで変化させれば、すべての組み合わせを試すことになる。
#include <stdio.h>
#define sizeofarray(A) (sizeof(A)/sizeof(A[0]))
int obj_len = 10 ;
int a[] = { 4 , 5 , 2 , 1 , 3 , 7 } ;
int main() {
int l_max = 1 << sizeofarray( a ) ;
for( int i = 1 ; i < l_max ; i++ ) {
// i は a[j]を使うか使わないかを表す2進数
// i = 5 の場合
// 5 = 0,0,0,1,0,1
// a[] 7,3,1,2,5,4
// ^ ^ = 長さは6
int sum = 0 ;
for( int j = 0 ; j < sizeofarray( a ) ; j++ ) {
// iの2進数の各bitに対応する長さを加算
if ( (i & (1 << j)) != 0 )
sum += a[ j ] ;
}
// 目的の長さを作れたので答えを表示
if ( sum == obj_len ) {
printf( "0x%x : " , i ) ;
for( int j = 0 ; j < sizeofarray( a ) ; j++ ) {
if ( (i & (1 << j)) != 0 ) {
printf( "%d " , a[ j ] ) ;
}
}
printf( "\n" ) ;
}
}
return 0 ;
}
このプログラムは再帰呼び出しを含まないので、プログラムの挙動も解りやすい。しかし、j番目を使うか使わないのか…という2つの状態しかない組み合わせ問題でしか使えない。今回の競技部門のように、↑,→,↓,←,回転右,回転左という6状態の場合は、使えない。
Flood fill アルゴリズム
再帰を使う他の事例として、図形の塗りつぶし問題で示す。(Wikipedia Flood-fill参照)
以下の image のような2次元配列が与えられたら、指定座標(x,y)を中心に周囲を塗りつぶす処理を作成せよ。
include <stdio.h>
// *は壁 SPCは白 この領域の指定位置を#で塗りつぶす。
char image1[10][10] = { // (4,4)始点で塗りつぶし後
"*********" , // *********
"* * *" , // * *###*
"* * *" , // * *###*
"* * *" , // * *####*
"*** ***" , // ***###***
"* * *" , // *####* *
"* * *" , // *###* *
"* * *" , // *###* *
"*********" , // *********
} ;
char image2[10][10] = { // 応用問題用の画像例
"*********" , // * のような隙間は通り抜けられる
"* * *" , // * ようにするにはどうすればいい?
"* ** *" , // **
"* ** *" , // ** これは通り抜けられない
"*** ***" , // **
"* * *" ,
"* * *" ,
"* * *" ,
"*********" ,
} ;
// 盤面を表示
void print_image( char image[10][10] ) {
for( int y = 0 ; y < 9 ; y++ ) {
for( int x = 0 ; x < 9 ; x++ ) {
printf( "%c" , image[y][x] ) ;
}
printf( "\n" ) ;
}
}
// 再帰呼び出しを使った flud_fill アルゴリズム
void flood_fill( char image[10][10] , int x , int y , char fill ) {
// image: 塗りつぶす画像
// x,y: 塗りつぶす場所
// fill: 書き込む文字
// 指定座標が空白なら
if ( image[y][x] == ' ' ) {
// その座標を埋める
image[y][x] = fill ;
//////////////////////////////////////
// ここに周囲をflud_fillする処理を書く //
//////////////////////////////////////
}
}
int main() {
print_image( image1 ) ;
flood_fill( image1 , 4 , 4 , '#' ) ;
print_image( image1 ) ;
return 0 ;
}
応用問題
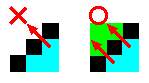
Wikipediaのflood-fill のプログラムの説明のアルゴリズムでは、左図黒のような斜めに並んだブロックは、境界として通り抜けられないようにつくられている。
そこで、斜めに並んだブロックは通り抜けられるルールとした場合のプログラムを記述せよ。
レポート提出
レポートでは、指定長を辺の組み合わせで作るテーマか、Flood-fill のテーマのいずれかにて、以下の内容をまとめてレポートとして提出すること。
-
- レポートの説明(自分の選んだテーマと自分なりの説明)
- プログラムリスト
- 動作確認の結果
電子情報棟学生用WiFiの設置
電子情報棟では、本館などの教室のネットワークとは別に、ネットワーク環境を活かした実験での利用ができるように無線LANのアクセスポイントを増設しました。
接続には下記のように設定してください。
- SSID : nitfc-ei-student
- セキュリティレベル:WPA2-エンタープライズ
- ログイン:<教育用システムID>
- 例:s53599ts (@以降は不要)
- パスワード:<教育用システムパスワード>
- [要注意] Microsoft365のパスワードではありません。
- 使用可能な部屋:4EI教室、5EI教室、EI棟3F演習室
- これに合わせ、4EI教室,5EI教室壁の有線LANもすぐに使えるように設定しました。
なお ferec_wlan_* のアクセスポイントは、将来的に撤去する予定です。
fukuikousen-bot の shorturl
福井高専HPの新規記事を Twitter につぶやく bot を動かしていたけど、 HP記事のURLがつぶやきにつかないようになっていた。
原因は、Perl の WWW::Shorten::TinyURL モジュールを使っていたけど、 ライセンスの関係などで、このモジュールが動かなくなっていたみたい。
Twitter の 140 文字制限があったから、TinyURL で 高専の記事 URL を 短いものにしていたけど、最近この制限も緩いし、高専の最新記事の タイトルもそんなに文字数が多くもないし、TinyURL など使わず、 そのままの URL でつぶやくようにした。
第32回高専プロコン2021(秋田)の要綱発表
第32回の高専プロコンの要項が発表となりました。
「集え!未来創造への限りなき想い」
- 課題部門:「 楽しく学び合える! 」
- 自由部門:
- 競技部門:「技術廻戦」
参加にチャレンジしたい人は、連絡してくださぃ。