2分ヒープとレポート課題

2分ヒープ(binary heap)

2分探索木では、１つのノードにつき2つのポインタを持ち、データ1件あたりのメモリの使用量が多い。通常の「配列の先頭から昇順にデータを並べる2分探索法」では、途中にデータを挿入する場合、データを後ろにずらす必要があるため、O(N)の処理時間を要する。

これらの問題の解決法の１つとして、2分ヒープがある。左右に均一に成長している2分探索木で、上から番号を以下の様に振ると、i番目のデータの左の枝は 2×i+1 番目、右の枝は 2×i+2 番目であることが判る。

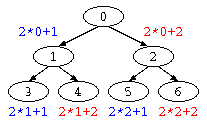
このような順序で配列にデータを保存する方法が2分ヒープである。この方式ならアルゴリズムの説明は省略するが、入れるべきノードの場所でのデータの入れ替えで実現できるため O( log( N ) )で挿入が可能となる。

import java.util.*;

public class Main {
    public static int find_heap( int[] array , int idx , int key ) {
        while( idx < array.length ) {
            if ( array[ idx ] == key )
                return idx ; // 見つかった
            else if ( array[ idx ] > key )
                idx = idx*2 + 1 ;
            else
                idx = idx*2 + 2 ;
        }
        return -1 ; // 見つからなかった
    }
    public static void main(String[] args) throws Exception {
        int[] a = { 53 , 11 , 86 , 10 , 22 , 65 , 92 } ;
        System.out.println( find_heap( a , 0 , 22 ) ) ;
    }
}

• 2分ヒープ(Paiza.io)

レポート課題

以下のようなデータを扱う2分探索木のプログラムを作成せよ。以下の箇条書き番号の中から、(出席番号 % 3+1)のデータについてプログラムを作ること。

1. 名前(name)と電話番号(phone)
2. 名前(name)と誕生日(year,mon,day)
3. 名前(name)とメールアドレス(mail)

プログラムは以下の機能を持つこと。

• 1行1件でデータを入力し、2分木に追加できること。
• 全データを昇順(or降順)で表示できること。
• 検索条件を入力し、目的のデータを探せること。

レポートでは、(a)プログラムリスト,(b)その説明,(c)動作検証結果,(d)考察 を記載すること。